
Полная версия
Диверсификация инвестиционного портфеля. Теория Марковица-Шарпа
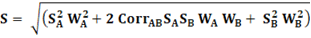
Посмотрим, какой будет риск портфеля с этими активами в зависимости от того, как коррелируют между собой доходности этих активов.
1.2.2.1. Коэффициент корреляции Corr=1
Пусть временные ряды доходностей активов A и B очень сильно коррелируют между собой с коэффициентом корреляции CorrAB=1.0. В этом случае в формуле для риска под квадратным корнем получаем полный квадрат, и квадратный корень извлекается. И тогда общий риск портфеля с двумя сильно коррелированными активами будет:
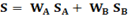
Получается, что для сильно коррелирующих активов риск портфеля, это просто взвешенный риск его активов. На графике «Риск-Доходность» на рис. 5 в этом случае получаем портфели на черном отрезке между точками A и B. Каждая точка черного отрезка соответствует своему соотношению весовых коэффициентов WA и WB.
Например, если 50 % всех своих финансов инвестор вложит в актив A и 50 % в актив B, то получаем портфель, показанный черной точкой на черном отрезке. Эта точка лежит в середине черного отрезка. У такого портфеля с равными вложениями в 2 актива с нашими данными получились следующие средняя доходность
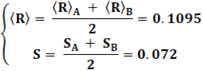
Теперь посмотрим на еще одном синтетическом примере, как это всё выглядит на временных графиках. На рис. 6. показано поведение цен двух активов с сильной корреляцией их доходностей за 43 торговых дня.
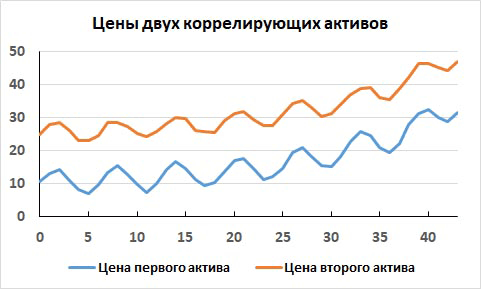
Рис. 6. Изменение цен двух активов с сильной корреляцией их доходностей за 43 торговых дня.
Эти цены меняются очень похоже друг на друга. Они одновременно растут и одновременно падают. Доходности этих активов в этом примере коррелируют друг с другом коэффициентом корреляции очень близким к единице: Corr = +0.95.
Средняя доходность первого актива на интервале 43 торговых дня
На рис. 7 показан график доходностей этих активов. Хорошо видно, что эти доходности одновременно друг с другом становятся отрицательными и одновременно становятся положительными. Отрицательные доходности означают убытки.
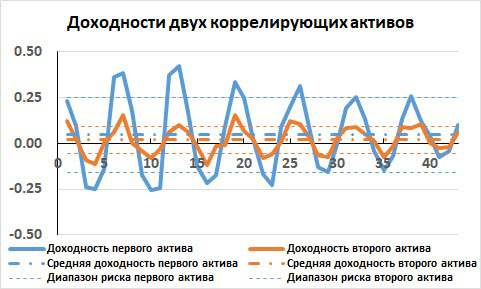
Рис. 7. Изменение доходностей двух сильно коррелирующих активов за 43 торговых дня, их средние доходности и диапазоны риска.
На этом же рисунке горизонтальными штрихпунктирными линиями показаны средние за интервал доходности этих активов. Хотя средние доходности находятся выше нуля, то есть активы за все 43 дня оказались не убыточные, но в конкретные торговые дни обе доходности могут быть одновременно отрицательными.
Наконец, на рис. 7 тонкими пунктирными линиями показаны диапазоны риска активов. Диапазон риска, это отклонение доходности вверх и вниз от средней доходности на величину стандартного отклонения, то есть на величину риска. Хорошо видно, что нижние границы этих диапазонов очень сильно залезают в отрицательную область доходностей.
На рис. 8 показаны эти же самые доходности двух активов и доходность портфеля, который состоит из этих активов с весовыми коэффициентами W1 = W2 = 0.5.
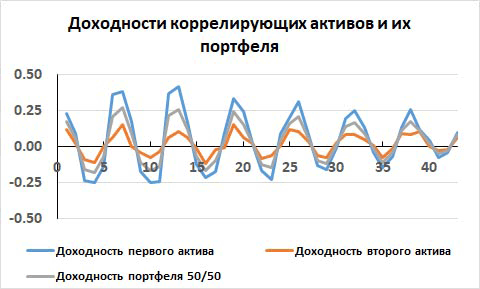
Рис. 8. Доходности двух сильно коррелирующих активов и их портфеля с долями 1/2.
Какое бы соотношение долей активов мы бы не взяли, кривая доходностей портфеля всегда будет находится между кривыми доходностей этих двух активов. Кривая доходностей портфеля, как бы заперта, между кривыми доходности сильно коррелирующих активов. Она будет расположена ближе к кривой первого или второго актива в зависимости от соотношения долей этих активов в портфеле: W1 и W2.
Средняя доходность портфеля
1.2.2.2. Коэффициент корреляции меньше единицы и больше минус единицы
Вернемся к нашему примеру с активами A и B из начала раздела 1.2.2. Если коэффициент корреляции временных рядов доходностей двух активов будет в диапазоне от -1 до +1 (-1
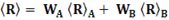
А в формуле для риска портфеля двух активов (см. последнюю формулу раздела 1.2.2), в общем случае, квадратный корень в аналитическом виде не извлекается. Но хорошо видно, что подкоренное выражение будет уменьшаться вместе с уменьшением коэффициента корреляции CorrAB. Значит, риск портфеля из двух активов будет уменьшаться вместе с уменьшением коэффициента корреляции.
Вот это и есть главный вывод теории Марковица. Чем коэффициент корреляции доходности активов меньше, тем меньше риск портфеля. Мы здесь этот вывод увидели на примере портфеля из двух активов.
На графике «Риск-Доходность» (см. рис. 5) портфели из двух активов будут уже располагаться не на отрезке, который соединяет два актива, а на кривых линиях, которые соединяют эти активы. Эти кривые имеют выпуклость в сторону меньшего риска.
На рис. 5 показано, как меняются линии местоположения портфелей для разных долей активов A и B, и разных коэффициентов корреляции. Разные цвета кривых на рис. 5 соответствуют разным коэффициентам корреляции CorrAB. А конкретные точки на кривой фиксированного цвета соответствуют разным соотношениям весов активов WA и WB.
Цветными точками на рис. 5 показаны портфели с минимальными рисками для данного коэффициента корреляции.
Черными точками на рис. 5 показаны положения портфелей с равными весами активов WA = WB = 0.5. Доходности таких портфелей одинаковые. Но риски этих портфелей тем меньше, чем меньше коэффициент корреляции между доходностями активов.
Обратите внимание, что равные веса активов еще не гарантируют, что получится портфель с минимальным риском. Хорошо видно, что цветные точки находятся левее черных точек на соответствующих цветных кривых.
1.2.2.3. Антикорреляция Corr=-1
При самой маленькой корреляции между доходностями активов (CorrAB=-1) кривые линии портфелей переходят в 2 отрезка, лежащих на прямых линиях, как показано голубым цветом на рис. 5. Эти отрезки касаются вертикальной оси координат в одной точке.
Но все точки на вертикальной оси координат соответствуют портфелям с нулевым риском. Значит, если доходности двух активов в точности антикоррелируют друг с другом, то можно так подобрать весовые коэффициенты этих двух активов, что результирующий портфель не будет иметь никакого риска (то есть станет безрисковым активом). Найдем эти весовые коэффициенты.
Если в последнюю формулу для риска из раздела 1.2.2 подставить CorrAB=-1, то квадратный корень извлекается в аналитическом виде и получаем результат для весов в виде:
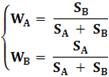
Итак, если портфель состоит только из двух активов, и доходности этих активов антикоррелируют, то получаем идеальную ситуацию: портфель становится безрисковым, если веса активов взаимно пропорциональны риску друг друга.
Снова посмотрим, как это всё выглядит на временных графиках для какого-нибудь синтетического примера. На рис. 9. показано поведение цен двух активов с сильной антикорреляцией их доходностей за 43 торговых дня.
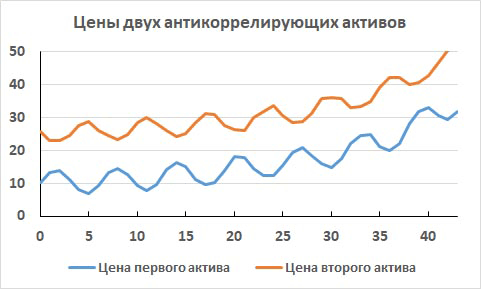
Рис. 9. Изменение цен двух активов с сильной антикорреляцией их доходностей за 43 торговых дня
Эти цены локально меняются очень по-разному. Когда цена одного актива растет, то цена другого падает, и, наоборот. Доходности этих активов в этом примере почти антикоррелируют друг с другом, с коэффициентом корреляции очень близким к минус единице: Corr = -0.91.
Средняя доходность первого актива на интервале 43 торговых дня
На рис. 10 показан график изменения доходностей этих активов за 43 дня. Хорошо видно, что, когда доходность первого актива становится положительной, доходность второго актива становится отрицательной, и, наоборот.
Поэтому убытки этих активов не складываются друг с другом. Когда доходность более волатильного актива сильно уходит в минус, в это время менее волатильный актив находится в плюсе по своей доходности и частично компенсирует убытки более волатильного актива. Понятно, что если долю менее волатильного актива взять побольше, а долю более волатильного поменьше, то можно так подобрать эти доли, что ухода в минус почти не будет.
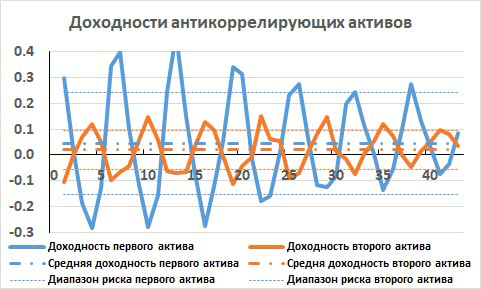
Рис. 10. Изменение доходностей двух сильно антикоррелирующих активов за 43 торговых дня, их средние доходности и диапазоны риска.
На этом же рис. 10 горизонтальными штрихпунктирными линиями показаны средние за интервал 43 торговых дня доходности этих активов. А тонкими пунктирными линиями показаны диапазоны риска активов. Это отклонения доходности вверх и вниз от среднего значения на величину стандартного отклонения, то есть на величину риска. У актива с большим риском диапазон риска шире, чем у актива с меньшим риском.
На рис. 11 показаны доходности двух портфелей, составленных из этих активов. Кривая синего цвета соответствует такому портфелю, который состоит из этих активов с весовыми коэффициентами W1 = W2 = 0.5. Хорошо видно, что даже такое наивное распределение средств уже сильно уменьшает волатильность портфеля. Риск портфеля стал всего S12 = 0.070. Это меньше, чем риски и первого и второго активов.
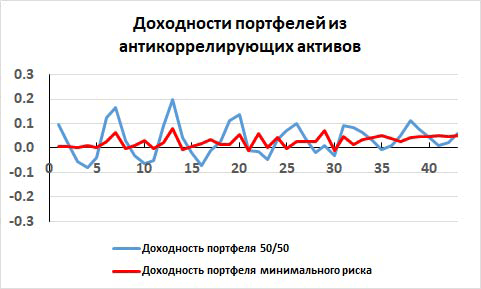
Рис. 11. Доходности портфеля с активами, у которых доходности сильно антикоррелируют.
Но наивная диверсификация в данном примере не является самой лучшей возможной диверсификацией. Если распределить средства инвестора в портфеле с такими весами, как W1 = 0.267 и W2 = 0.733, то получим колебания доходности портфеля еще меньше. На рис. 11 изменение доходности такого оптимального портфеля показана кривой красного цвета.
Если бы в данном примере у нас была бы точная антикорреляция (Corr12 = -1), то мы получили бы не кривую линию красного цвета, а прямую горизонтальную линию на уровне доходности
Поэтому оптимальный портфель с минимальным риском у нас не имеет нулевого риска. Но его риск очень маленький: S12 = 0.057. Это меньше, чем риск наивного портфеля с одинаковыми весами, который, как было уже показано выше, равен S12 = 0.070.
1.2.3. Пример с тремя активами
На примере портфеля с двумя активами мы всё так очень подробно рассмотрели для того, чтобы читатель понимал теорию Марковица на интуитивном уровне. Далее считаем, что интуитивно всё уже понятно, поэтому дальнейшее рассмотрение проведем уже не так подробно.
Если активов в портфеле будет уже не 2, а 3, то всевозможные портфели с разными весами этих активов будут располагаться уже не на кривой линии, а на некоторой площади на плоскости "Риск-Доходность".
Добавим к активам A и B из нашего синтетического примера еще третий актив C со средней доходностью
1.2.3.1. Все коэффициенты корреляции равны единице
Если все 3 актива максимально коррелируют друг с другом с парными коэффициентами корреляции равными единице (CorrAB = CorrBC = CorrCA = +1), то на графике «Риск-Доходность» все возможные портфели располагаются внутри треугольника ABC, как показано на рис. 12. На рисунке эти точки внутри треугольника показаны серым цветом.
Отрезок AB соответствует таким портфелям, когда актив C имеет нулевой вес WC = 0. Этот случай мы рассматривали в предыдущем разделе. Аналогично, отрезок BC соответствует таким портфелям, когда актив A имеет нулевой вес WA = 0. И, наконец, отрезок CA соответствует таким портфелям, когда актив B имеет нулевой вес WB = 0.
Серые точки внутри треугольника ABC соответствуют ситуации, когда все 3 веса отличаются от нуля. В центре серого треугольника находится портфель с равными весами активов: WA = WB = WC = 1/3.
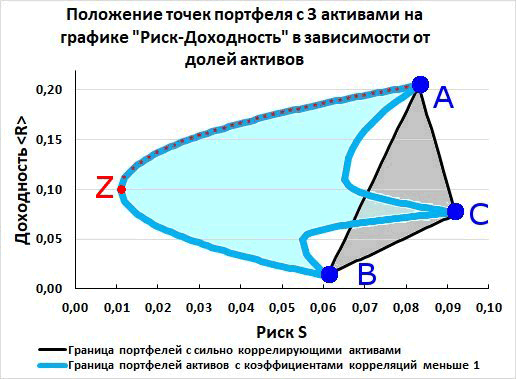
Рис. 12. График «Риск-Доходность» для трех активов.
1.2.3.2. Все коэффициенты корреляции меньше единицы
А если все три коэффициента корреляции меньше единицы (CorrAB < 1, CorrBC < 1 и CorrCA < 1), то зона всех возможных портфелей на графике «Риск-Доходность» сдвигается влево в сторону уменьшения риска. На рис. 12 показан пример такой зоны для таких портфелей. Эта зона закрашена светло-голубым цветом. Эта область ограничена тремя кривыми линиями, которые на рисунке показаны голубым цветом.
Здесь важно понимать, что дуга AB, это теперь уже не те дуги AB, которые мы видели на рис. 5. В формировании самой крайней левой дуги, в общем случае, принимают участие все 3 актива, а не только 2 самых менее рискованных активов A и B.
В общем случае, у самого наименее рискованного портфеля Z на рис. 12 все три весовых коэффициента отличаются от нуля (WA ≠ 0, WB ≠ 0 и WC ≠ 0). При этом вес самого рискованного актива WC в портфеле Z может быть достаточно большим, если активы A и B сильнее коррелируют друг с другом, чем они по отдельности коррелируют с активом C, то есть CorrAB > CorrBC и CorrAB > CorrCA.
То есть для уменьшения риска портфеля часто бывает более эффективно взять самые большие весовые коэффициенты не у самых менее рисковых активов, а у тех активов, которые меньше коррелируют и/или больше антикоррелируют с другими активами портфеля. И эта задача нахождения оптимальных долей активов для трех активов становится уже очень нетривиальной. В общем случае эта математическая задача уже не решается в Экселе. В разделе 4 мы познакомимся с одним онлайновым инструментом, который решает эту задачу.
1.2.3.3. Эффективная Граница
Задача формирования хорошего инвестиционного портфеля из трех активов A, B и C состоит в том, чтобы найти такие весовые коэффициенты WA, WB и WC долей этих активов, которые давали бы максимальную доходность и минимальный риск.
Понятно, что светло-голубая область на графике «Риск-Доходность» на рис. 12 около точки B нам никак не подходит, так как там находятся портфели с такими весами, которые дают плохую доходность. Также нам не подходит и светло-голубая область около точки С, так как это портфели со слишком большим риском.
В точке A находится портфель с самой высокой доходностью. Это портфель из одного единственного актива A, с весовыми коэффициентами WA = 1, WB = WC = 0. Но этот портфель имеет очень большой риск.
В точке Z находится портфель с самым минимальным риском. Но доходность этого портфеля почти в 2 раза ниже, чем доходность портфеля, который состоит только из одного актива A.
Таким образом, нам не подходит и самый доходный портфель из-за его высокого риска и не подходит портфель минимального риска из-за его плохой доходности. Нам хочется, чтобы портфель был одновременно и самым доходным и самым менее рискованным среди всех возможных портфелей.
Увы, но в жизни так не бывает, чтобы был одновременно и минимальный риск, и высокие доходы. Это, кстати, справедливо для любой сферы бизнеса и инвестиций. Портфельные инвестиции в биржевые активы не являются каким-то исключением.
Можно только из всех портфелей с фиксированным риском найти самый доходный портфель. Или, наоборот, можно только среди всех портфелей с фиксированным доходом найти наименее рискованный портфель.
Все такие портфели на рис. 12 находятся на дуге AZ, которая показана пунктирной линией. Это и есть место расположения самых лучших портфелей. Более лучшие портфели по доходности (с фиксированным риском) не существуют, так как нет портфелей, которые находятся выше этой кривой. И также не существуют менее рискованные портфели (с фиксированной доходностью), так как нет портфелей, которые находятся левее этой кривой.
Эта кривая, которая ограничивает область всех допустимых портфелей сверху и слева, называется Эффективная Граница.
Обычно, инвесторы хотят так подобрать весовые коэффициенты активов, чтобы их портфель попал на Эффективную Границу или был как можно ближе к ней.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «Литрес».
Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.






