 полная версия
полная версияTime and Tide: A Romance of the Moon
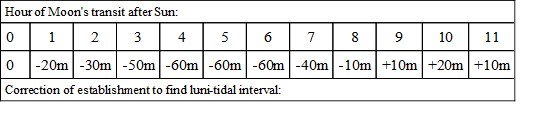
Thus at a port where the establishment was 3h. 25m., let us suppose that the transit of the moon took place at 6 P.M.; then we correct the establishment by -60m., and find the luni-tidal interval to be 2h. 25m., and accordingly the high water takes place at 8h. 25m. P.M.
But even this method is only an approximation. The study of the tides is based on accurate observation of their rise and fall on different places round the earth. To show how these observations are to be made, and how they are to be discussed and reduced when they have been made, I may refer to the last edition of the Admiralty Manual of Scientific Inquiry, 1886. For a complete study of the tides at any port a self-registering tide-gauge should be erected, on which not alone the heights and times of high and low water should be depicted, but also the continuous curve which shows at any time the height of the water. In fact, the whole subject of the practical observation and discussion and prediction of tides is full of valuable instruction, and may be cited as one of the most complete examples of the modern scientific methods.
In the first place, the tide-gauge itself is a delicate instrument; it is actuated by a float which rises and falls with the water, due provision being made that the mere influence of waves shall not make it to oscillate inconveniently. The motion of the float when suitably reduced by mechanism serves to guide a pencil, which, acting on the paper round a revolving drum, gives a faithful and unintermitting record of the height of the water.
Thus what the tide-gauge does is to present to us a long curved line of which the summits correspond to the heights of high water, while the depressions are the corresponding points of low water. The long undulations of this curve are, however, very irregular. At spring tides, when the sun and the moon conspire, the elevations rise much higher and the depressions sink much lower than they do at neap tides, when the high water raised by the moon is reduced by the action of the sun. There are also many minor irregularities which show the tides to be not nearly such simple phenomena as might be at first supposed. But what we might hastily think of as irregularities are, in truth, the most interesting parts of the whole phenomena. Just as in the observations of the planets the study of the perturbations has led us to results of the widest interest and instruction, so it is these minor phenomena of the tides which seem most pregnant with scientific interest.
The tide-gauge gives us an elaborate curve. How are we to interpret that curve? Here indeed a most beautiful mathematical theorem comes to our aid. Just as ordinary sounds consist of a number of undulations blended together, so the tidal wave consists of a number of distinct undulations superposed. Of these the ordinary lunar tide and the ordinary solar tide are the two principal; but there are also minor undulations, harmonics, so to speak, some originating from the moon, some originating from the sun, and some from both bodies acting in concert.
In the study of sound we can employ an acoustic apparatus for the purpose of decomposing any proposed note, and finding not only the main undulation itself, but the several superposed harmonics which give to the note its timbre. So also we can analyze the undulation of the tide, and show the component parts. The decomposition is effected by the process known as harmonic analysis. The principle of the method may be very simply described. Let us fix our attention on any particular “tide,” for so the various elements are denoted. We can always determine beforehand, with as much accuracy as we may require, what the period of that tide will be. For instance, the period of the lunar semi-diurnal tide will of course be half the average time occupied by the moon to travel round from the meridian of any place until it regains the same meridian; the period of the lunar diurnal tide will be double as great; and there are fortnightly tides, and others of periods still greater. The essential point to notice is, that the periods of these tides are given by purely astronomical considerations from the periods of the motions theory, and do not depend upon the actual observations.
We measure off on the curve the height of the tide at intervals of an hour. The larger the number of such measures that are available the better; but even if there be only three hundred and sixty or seven hundred and twenty consecutive hours, then, as shown by Professor G. H. Darwin in the Admiralty Manual already referred to, it will still be possible to obtain a very competent knowledge of the tides in the particular port where the gauge has been placed.
The art (for such indeed it may be described) of harmonic analysis consists in deducing from the hourly observations the facts with regard to each of the constituent tides. This art has been carried to such perfection, that it has been reduced to a very simple series of arithmetical operations. Indeed it has now been found possible to call in the aid of ingenious mechanism, by which the labours of computation are entirely superseded. The pointer of the harmonic analyzer has merely to be traced over the curve which the tide-gauge has drawn, and it is the function of the machine to decompose the composite undulation into its parts, and to exhibit the several constituent tides whose confluence gives the total result.
As if nothing should be left to complete the perfection of a process which, both from its theoretical and its practical sides, is of such importance, a machine for predicting tides has been designed, constructed, and is now in ordinary use. When by the aid of the harmonic analysis the effectiveness of the several constituent tides affecting a port have become fully determined, it is of course possible to predict the tides for that port. Each “tide” is a simple periodic rise and fall, and we can compute for any future time the height of each were it acting alone. These heights can all be added together, and thus the height of the water is obtained. In this way a tide-table is formed, and such a table when complete will express not alone the hours and heights of high water on every day, but the height of the water at any intervening hour.
The computations necessary for this purpose are no doubt simple, so far as their principle is concerned; but they are exceedingly tedious, and any process must be welcomed which affords mitigation of a task so laborious. The entire theory of the tides owes much to Sir William Thomson in the methods of observation and in the methods of reduction. He has now completed the practical parts of the subject by inventing and constructing the famous tide-predicting engine.
The principle of this engine is comparatively simple. There is a chain which at one end is fixed, and at the other end carries the pencil which is pressed against the revolving drum on which the prediction is to be inscribed. Between its two ends the chain passes up and down over pulleys. Each pulley corresponds to one of the “tides,” and there are about a dozen altogether, some of which exercise but little effect. Of course if the centres of the pulleys were all fixed the pen could not move, but the centre of each pulley describes a circle with a radius proportional to the amplitude of the corresponding tide, and in a time proportional to the period of that tide. When these pulleys are all set so as to start at the proper phases, the motion is produced by turning round a handle which makes the drum rotate, and sets all the pulleys in motion. The tide curve is thus rapidly drawn out; and so expeditious is the machine, that the tides of a port for an entire year can be completely worked out in a couple of hours.
While the student or the philosopher who seeks to render any account of the tide on dynamical grounds is greatly embarrassed by the difficulties introduced by friction, we, for our present purpose in the study of the great romance of modern science opened up to us by the theory of the tides, have to welcome friction as the agent which gives to the tides their significance from our point of view.
There is the greatest difference between the height of the rise and fall of the tide at different localities. Out in mid-ocean, for instance, an island like St. Helena is washed by a tide only about three feet in range; an enclosed sea like the Caspian is subject to no appreciable tides whatever, while the Mediterranean, notwithstanding its connection with the Atlantic, is still only subject to very inconsiderable tides, varying from one foot to a few feet. The statement that water always finds its own level must be received, like many another proposition in nature, with a considerable degree of qualification. Long ere one tide could have found its way through the Straits of Gibraltar in sufficient volume to have appreciably affected the level of the great inland sea, its effects would have been obliterated by succeeding tides. On the other hand, there are certain localities which expose a funnel-shape opening to the sea; into these the great tidal wave rushes, and as it passes onwards towards the narrow part, the waters become piled up so as to produce tidal phenomena of abnormal proportions. Thus, in our own islands, we have in the Bristol Channel a wide mouth into which a great tide enters, and as it hurries up the Severn it produces the extraordinary phenomenon of the Bore. The Bristol Channel also concentrates the great wave which gives Chepstow and Cardiff a tidal range of thirty-seven or thirty-eight feet at springs, and forces the sea up the river Avon so as to give Bristol a wonderful tide. There is hardly any more interesting spot in our islands for the observation of tides than is found on Clifton Suspension Bridge. From that beautiful structure you look down on a poor and not very attractive stream, which two hours later becomes transformed into a river of ample volume, down which great ships are navigated. But of all places in the world, the most colossal tidal phenomena are those in the Bay of Fundy. Here the Atlantic passes into a long channel whose sides gradually converge. When the great pulse of the tide rushes up this channel, it is gradually accumulated into a mighty volume at the upper end, the ebb and flow of which at spring tides extends through the astonishing range of not less than fifty feet.
These discrepancies between the tides at different places are chiefly due to the local formations of the coasts and the sea-beds. Indeed, it seems that if the whole earth were covered with an uniform and deep ocean of water, the tides would be excessively feeble. On no other supposition can we reasonably account for the fact that our barometric records fail to afford us any very distinct evidence as to the existence of tides in the atmosphere. For you will, of course, remember that our atmosphere may be regarded as a deep and vast ocean of air, which embraces the whole earth, extending far above the loftiest summits of the mountains.
It is one of the profoundest of nature's laws that wherever friction takes place, energy has to be consumed. Perhaps I ought rather to say transformed, for of course it is now well known that consumption of energy in the sense of absolute loss is impossible. Thus, when energy is expended in moving a body in opposition to the force of friction, or in agitating a liquid, the energy which disappears in its mechanical form reappears in the form of heat. The agitation of water by paddles moving through it warms the water, and the accession of heat thus acquired measures the energy which has been expended in making the paddles rotate. The motion of a liquid of which the particles move among each other with friction, can only be sustained by the incessant degradation of energy from the mechanical form into the lower form of diffused heat. Thus the very fact that the tides are ebbing and flowing, and that there is consequently incessant friction going on among all the particles of water in the ocean, shows us that there must be some great store of energy constantly available to supply the incessant draughts made upon it by the daily oscillation of the tides. In addition to the mere friction between the particles of water, there are also many other ways in which the tides proclaim to us that there is some great hoard of energy which is continually accessible to their wants. Stand on the bank of an estuary or river up and down which a great tidal current ebbs and flows; you will see the water copiously charged with sediment which the tide is bearing along. Engineers are well aware of the potency of the tide as a vehicle for transporting stupendous quantities of sand or mud. A sand-bank impedes the navigation of a river; the removal of that sand-bank would be a task, perhaps, conceivably possible by the use of steam dredges and other appliances, whereby vast quantities of sand could be raised and transported to another locality where they would be innocuous. It is sometimes possible to effect the desired end by applying the power of the tide. A sea-wall judiciously thrown out will sometimes concentrate the tide into a much narrower channel. Its daily oscillations will be accomplished with greater vehemence, and as the tide rushes furiously backwards and forwards over the obstacle, the incessant action will gradually remove it, and the impediment to navigation may be cleared away. Here we actually see the tides performing a piece of definite and very laborious work, to accomplish which by the more ordinary agents would be a stupendous task.
In some places the tides are actually harnessed so as to accomplish useful work. I have read that underneath old London Bridge there used formerly to be great water-wheels, which were turned by the tide as it rushed up the river, and turned again, though in the opposite way, by the ebbing tide. These wheels were, I believe, employed to pump up water, though it does not seem obvious for what purposes the water would have been suitable. Indeed in the ebb and flow all round our coasts there is a potential source of energy which has hitherto been allowed to run to waste. The tide could be utilized in various ways. Many of you will remember the floating mills on the Rhine. They are vessels like paddle steamers anchored in the rapid current. The flow of the river makes the paddles rotate, and thus the machinery in the interior is worked. Such craft moored in a rapid tide-way could also be made to convey the power of the tides into the mechanism of the mill. Or there is still another method which has been employed, and which will perhaps have a future before it in those approaching times when the coal-cellars of England shall be exhausted. Imagine on the sea-coast a large flat extent which is inundated twice every day by the tide. Let us build a stout wall round this area, and provide it with a sluice-gate. Open the gate as the tide rises, and the great pond will be filled; then at the moment of high water close the sluice, and the pond-full will be impounded. If at low tide the sluice be opened the water will rush tumultuously out. Now suppose that a water-wheel be provided, so that the rapid rush of water from the exit shall fall upon its blades; then a source of power is obviously the result.
At present, however, such a contrivance would naturally find no advocates, for of course the commercial aspect of the question is that which will decide whether the scheme is practicable and economical. The issue indeed can be very simply stated. Suppose that a given quantity of power be required—let us say that of one hundred horse. Then we have to consider the conditions under which a contrivance of the kind we have sketched shall yield a power of this amount. Sir William Thomson, in a very interesting address to the British Association at York in 1881, discussed this question, and I shall here make use of the facts he brought forward on that occasion. He showed that to obtain as much power as could be produced by a steam-engine of one hundred horse power, a very large reservoir would be required. It is doubtful indeed whether there would be many localities on the earth which would be suitable for the purpose. Suppose, however, an estuary could be found which had an area of forty acres; then if a wall were thrown across the mouth so that the tide could be impounded, the total amount of power that could be yielded by a water-wheel worked by the incessant influx and efflux of the tide would be equal to that yielded by the one hundred horse engine, running continuously from one end of the year to the other.
There are many drawbacks to a tide-mill of this description. In the first place, its situation would naturally be far removed from other conveniences necessary for manufacturing purposes. Then too there is the great irregularity in the way in which the power is rendered available. At certain periods during the twenty-four hours the mill would stop running, and the hours when this happened would be constantly changing. The inconvenience from the manufacturer's point of view of a deficiency of power during neap tides might not be compensated by the fact that he had an excessive supply of power at spring-tides. Before tide-mills could be suitable for manufacturing purposes, some means must be found for storing away the energy when it is redundant, and applying it when its presence is required. We should want in fact for great sources of energy some contrivance which shall fulfil the same purpose as the accumulators do in an electrical installation.
Even then, however, the financial consideration remains, as to whether the cost of building the dam and maintaining the tide-mill in good order will not on the whole exceed the original price and the charges for the maintenance of a hundred horse power steam-engine. There cannot be a doubt that in this epoch of the earth's history, so long as the price of coal is only a few shillings a ton, the tide-mill, even though we seem to get its power without current expense, is vastly more expensive than a steam-engine. Indeed, Sir William Thomson remarks, that wherever a suitable tidal basin could be found, it would be nearly as easy to reclaim the land altogether from the sea. And if this were in any locality where manufactures were possible, the commercial value of forty acres of reclaimed land would greatly exceed all the expenses attending the steam-engine. But when the time comes, as come it apparently will, that the price of coal shall have risen to several pounds a ton, the economical aspect of steam as compared with other prime movers will be greatly altered; it will then no doubt be found advantageous to utilize great sources of energy, such as Niagara and the tides, which it is now more prudent to let run to waste.
For my argument, however, it matters little that the tides are not constrained to do much useful work. They are always doing work of some kind, whether that be merely heating the particles of water by friction, or vaguely transporting sand from one part of the ocean to the other. Useful work or useless work are alike for the purpose of my argument. We know that work can never be done unless by the consumption or transformation of energy. For each unit of work that is done—whether by any machine or contrivance, by the muscles of man or any other animal, by the winds, the waves, or the tides, or in any other way whatever—a certain equivalent quantity of energy must have been expended. When, therefore, we see any work being performed, we may always look for the source of energy to which the machine owes its efficiency. In fact, it is the old story illustrated, that perpetual motion is impossible. A mechanical device, however ingenious may be the construction, or however accurate the workmanship, can never possess what is called perpetual motion. It is needless to enter into details of any proposed contrivance of wheels, of pumps, of pulleys; it is sufficient to say that nothing in the shape of mechanism can work without friction, that friction produces heat, that heat is a form of energy, and that to replace the energy consumed in producing the heat there must be some source from which the machine is replenished if its motion is to be continued indefinitely.
Hence, as the tides may be regarded as a machine doing work, we have to ascertain the origin of that energy which they are continually expending. It is at this point that we first begin to feel the difficulties inherent in the theory of tidal evolution. I do not mean difficulties in the sense of doubts, for up to the present I have mentioned no doubtful point. When I come to such I shall give due warning. By difficulties I now mean points which it is not easy to understand without a little dynamical theory; but we must face these difficulties, and endeavour to elucidate them as well as we can.
Let us first see what the sources of energy can possibly be on which the tides are permitted to draw. Our course is simplified by the fact that the energy of which we have to speak is of a mechanical description, that is to say, not involving heat or other more obscure forms of energy. A simple type of energy is that possessed by a clock-weight after the clock has been wound. A store of power is thus laid up which is gradually doled out during the week in small quantities, second by second, to sustain the motion of the pendulum. The energy in this case is due to the fact that the weight is attracted by the earth, and is yielded according as the weight sinks downwards. In the separation between two mutually attracting bodies, a store of energy is thus implied. What we learn from an ordinary clock may be extended to the great bodies of the universe. The moon is a gigantic globe separated from our earth by a distance of 240,000 miles. The attraction between these two bodies always tends to bring them together. No doubt the moon is not falling towards the earth as the descending clock-weight is doing. We may, in fact, consider the moon, so far as our present object is concerned, to be revolving almost in a circle, of which the earth is the centre. If the moon, however, were to be stopped, it would at once commence to rush down towards the earth, whither it would arrive with an awful crash in the course of four or five days. It is fortunately true that the moon does not behave thus; but it has the ability of doing so, and thus the mere separation between the earth and the moon involves the existence of a stupendous quantity of energy, capable under certain conditions of undergoing transformation.
There is also another source of mechanical energy besides that we have just referred to. A rapidly moving body possesses, in virtue of its motion, a store of readily available energy, and it is easy to show that energy of this type is capable of transformation into other types. Think of a cannon-ball rushing through the air at a speed of a thousand feet per second; it is capable of wreaking disaster on anything which it meets, simply because its rapid motion is the vehicle by which the energy of the gunpowder is transferred from the gun to where the blow is to be struck. Had the cannon been directed vertically upwards, then the projectile, leaving the muzzle with the same initial velocity as before, would soar up and up, with gradually abating speed, until at last it reached a turning-point, the elevation of which would depend upon the initial velocity. Poised for a moment at the summit, the cannon-ball may then be likened to the clock-weight, for the entire energy which it possessed by its motion has been transformed into the statical energy of a raised weight. Thus we see these two forms of energy are mutually interchangeable. The raised weight if allowed to fall will acquire velocity, or the rapidly moving weight if directed upwards will acquire altitude.
The quantity of energy which can be conveyed by a rapidly moving body increases greatly with its speed. For instance, if the speed of the body be doubled, the energy will be increased fourfold, or, in general, the energy which a moving body possesses may be said to be proportional to the square of its speed. Here then we have another source of the energy present in our earth-moon system; for the moon is hurrying along in its path with a speed of two-thirds of a mile per second, or about twice or three times the speed of a cannon-shot. Hence the fact that the moon is continuously revolving in a circle shows us that it possesses a store of energy which is nine times as great as that which a cannon-ball as massive as the moon, and fired with the ordinary velocity, would receive from the powder which discharged it.



