The Number Mysteries: A Mathematical Odyssey through Everyday Life

The Ancient Chinese even had a concept of negative number, which they represented by different-coloured bamboo sticks. The use of black and red ink in Western accounting is thought to have originated from the Chinese practice of using red and black sticks, although intriguingly the Chinese used black sticks for negative numbers.

The Chinese were probably one of the first cultures to single out the primes as important numbers. They believed that each number had its own gender—even numbers were female and odd numbers male. They realized that some odd numbers were rather special. For example, if you have 15 stones, there is a way to arrange them into a nice-looking rectangle, in three rows of five. But if you have 17 stones you can’t make a neat array: all you can do is line them up in a straight line. For the Chinese, the primes were therefore the really macho numbers. The odd numbers, which aren’t prime, though they were male, were somehow rather effeminate.

This Ancient Chinese perspective homed in on the essential property of being prime, because the number of stones in a pile is prime if there is no way to arrange them into a nice rectangle.

We’ve seen how the Egyptians used pictures of frogs to depict numbers, the Maya drew dots and dashes, the Babylonians made wedges in clay, the Chinese arranged sticks, and in Hebrew culture letters of the alphabet stood for numbers. Although the Chinese were probably the first to single out the primes as important numbers, it was another culture that made the first inroads into uncovering the mysteries of these enigmatic numbers: the Ancient Greeks.

How the Greeks used sieves to cook up the primes

Here’s a systematic way discovered by the Ancient Greeks which is very effective at finding small primes. The task is to find an efficient method that will knock out all the non-primes. Write down the numbers from 1 to 100. Start by striking out number 1. (As I have mentioned, though the Greeks believed 1 to be prime, in the twenty-first century we no longer consider it to be.) Move to the next number, 2. This is the first prime. Now strike out every second number after 2. This effectively knocks out everything in the 2 times table, eliminating all the even numbers except for 2. Mathematicians like to joke that 2 is the odd prime because it’s the only even prime … but perhaps humour isn’t a mathematician’s strong point.

FIGURE 1.18 Strike out every second number after 2.

Now take the lowest number which hasn’t been struck out, in this case 3, and systematically knock out everything in the 3 times table:

FIGURE 1.19 Now strike out every third number after 3.

Because 4 has already been knocked out, we move next to the number, 5, and strike out every fifth number on from 5. We keep repeating this process, going back to the lowest number n that hasn’t yet been eliminated, and then strike out all the numbers n places ahead of it:

FIGURE 1.20 Finally we are left with the primes from 1 to 100.

The beautiful thing about this process it that it is very mechanical—it doesn’t require much thought to implement. For example, is 91 a prime? With this method you don’t have to think. 91 would have been struck out when you knocked out every 7th number on from 7 because 91=7×13.91 often catches people out because we tend not to learn our 7 times table up to 13.

This systematic process is a good example of an algorithm, a method of solving a problem by applying a specified set of instructions—which is basically what a computer program is. This particular algorithm was discovered two millennia ago in one of the hotbeds of mathematical activity at the time: Alexandria, in present-day Egypt. Back then, Alexandria was one of the outposts of the great Greek empire and boasted one of the finest libraries in the world. It was during the third century BC that the librarian Eratosthenes came up with this early computer program for finding primes.

It is called the sieve of Eratosthenes, because each time you knock out a group of non-primes it is as if you are using a sieve, setting the gaps between the wires of the sieve according to each new prime you move on to. First you use a sieve where the wires are 2 apart. Then 3 apart. Then 5 apart. And so on. The only trouble is that the method soon becomes rather inefficient if you try to use it to find bigger and bigger primes.

As well as sieving for primes and looking after the hundreds of thousands of papyrus and vellum scrolls in the library, Eratosthenes also calculated the circumference of the Earth and the distance of the Earth to the Sun and the Moon. The Sun he calculated to be 804,000,000 stadia from the Earth—although his unit of measurement perhaps makes judging the accuracy a little difficult. What size stadium are we meant to use: Wembley, or something smaller, like Loftus Road?

In addition to measuring the solar system, Eratosthenes charted the course of the Nile and gave the first correct explanation for why it kept flooding: heavy rains at the river’s distant sources in Ethiopia. He even wrote poetry. Despite all this activity, his friends gave him the nickname Beta—because he never really excelled at anything. It is said that he starved himself to death after going blind in old age.

You can use your snakes and ladders board on the cover to put the Sieve of Eratosthenes into operation. Take a pile of pasta and place pieces on each of the numbers as you knock them out. The numbers left uncovered will be the primes.

How long would it take to write a list of all the primes?

Anyone who tried to write down a list of all the primes would be writing for ever, because there are infinitely many of these numbers. What makes us so confident that we’d never come to the last prime, that there will always be another one waiting out there for us to add to the list? It is one of the greatest achievements of the human brain that with just a finite sequence of logical steps we can capture infinity.

The first person to prove that the primes go on for ever was a Greek mathematician living in Alexandria, called Euclid. He was a student of Plato’s, and he also lived during the third century BC, though it appears he was about 50 years older than the librarian Eratosthenes.

To prove that there must be infinitely many primes, Euclid started by asking whether, on the contrary, it was possible that there were, in fact, a finite number of primes. This finite list of primes would have to have the property that every other number can be produced by multiplying together primes from this finite list. For example, suppose that you thought that the list of all the primes consisted of just the three numbers 2, 3 and 5. Could every number be built up by multiplying together different combinations of 2s, 3s and 5s? Euclid concocted a way to build a number that could never be captured by these three prime numbers. He began by multiplying together his list of primes to make 30. Then—and this was his act of genius—he added 1 to this number to make 31. None of the primes on his list, 2, 3 or 5, would divide into it exactly. You always got remainder 1.

Euclid knew that all numbers are built by multiplying together primes, so what about 31? Since it can’t be divided by 2, 3 or 5, there had to be some other primes, not on his list, that created 31. In fact, 31 is a prime itself, so Euclid had created a ‘new’ prime. You might say that we could just add this new prime number to the list. But Euclid can then play the same trick again. However big the table of primes, Euclid can just multiply the list of primes together and add 1. Each time he can create a number which leaves remainder 1 on division by any of the primes on the list, so this new number has to be divisible by primes not on the list. In this way Euclid proved that no finite list could ever contain all the primes. Therefore there must be an infinite number of primes.

Although Euclid could prove that the primes go on for ever, there was one problem with his proof—it didn’t tell you where the primes are. You might think that his method produces a way of generating new primes. After all, when we multiplied 2, 3 and 5 together and added 1, we got 31, a new prime. But it doesn’t always work. For example, consider the list of primes 2, 3, 5, 7, 11 and 13. Multiply them all together: 30,030. Now add 1 to this number: 30,031. This number is not divisible by any of the primes from 2 to 13, because you always get remainder 1. However, it isn’t a prime number since it is divisible by the two primes 59 and 509, and they weren’t on our list. In fact, mathematicians still don’t know whether the process of multiplying a finite list of primes together and adding 1 infinitely often gives you a new prime number.

There’s a video available of my football team in their prime number kit explaining why there are infinitely many primes. Visit http://bit.ly/Primenumbersfootball or use your smartphone to scan this code.

Why are my daughters’ middle names 41 and 43?

If we can’t write down the primes in one big table, then perhaps we can try to find some pattern to help us to generate the primes. Is there some clever way to look at the primes you’ve got so far, and know where the next one will be?

Here are the primes we discovered by using the Sieve of Eratosthenes on the numbers from 1 to 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53,

59, 61, 67, 71, 73, 79, 83, 89, 97

The problem with the primes is that it can be really difficult to work out where the next one will be, because there don’t seem to be any patterns in the sequence that will help us to help locate them. In fact, they look more like a set of lottery ticket numbers than the building blocks of mathematics. Like waiting for a bus, you can have a huge gap with no primes and then suddenly several come along in quick succession. This behaviour is very characteristic of random processes, as we shall see in Chapter 3.

Apart from 2 and 3, the closest that two prime numbers can be is two apart, like 17 and 19 or 41 and 43, since the number between each pair is always even and therefore not prime. These pairs of very close primes are called twin primes. With my obsession for primes, my twin daughters almost ended up with the names 41 and 43. After all, if Chris Martin and Gwyneth Paltrow can call their baby Apple, and Frank Zappa can call his daughters Moon Unit and Diva Thin Muffin Pigeen, why can’t my twins be 41 and 43? My wife was not so keen, so these have had to remain my ‘secret’ middle names for the girls.

Although primes get rarer and rarer as you move out into the universe of numbers, it’s extraordinary how often another pair of twin primes pops up. For example, after the prime 1,129 you don’t find any primes in the next 21 numbers, then suddenly up pop the twin primes 1,151 and 1,153. And when you pass the prime 102,701 you have to plough through 59 non-primes, and then the pair of primes 102,761 and 102,763 suddenly appear. The largest twin primes discovered by the beginning of 2009 have 58,711 digits. Given that it only takes a number with 80 digits to describe the number of atoms in the observable universe, these numbers are ridiculously large.

But are there more beyond these two twins? Thanks to Euclid’s proof, we know that we’re going to find infinitely many more primes, but are we going to keep on coming across twin primes? As yet, nobody has come up with a clever proof like Euclid’s to show why there are infinitely many of these twin primes.

At one stage it seemed that twins might have been the key to unlocking the secret of prime numbers. In The Man Who Mistook His Wife for a Hat, Oliver Sacks describes the case of two real-life autistic savant twins who used the primes as a secret language. The twin brothers would sit in Sacks’s clinic, swapping large numbers between themselves. At first Sacks was mystified by their dialogue, but one night he cracked the secret to their code. Swotting up on some prime numbers of his own, he decided to test his theory. The next day he joined the twins as they sat exchanging six-digit numbers. After a while Sacks took advantage of a pause in the prime number patter to announce a seven-digit prime, taking the twins by surprise. They sat thinking for a while, since this was stretching the limit of the primes they had been exchanging to date, then they smiled simultaneously, as if recognizing a friend.

During their time with Sacks, they managed to reach primes with nine digits. Of course, no one would find it remarkable if they were simply exchanging odd numbers or perhaps even square numbers, but the striking thing about what they were doing is that the primes are so randomly scattered. One explanation for how they managed it relates to another ability the twins had. Often they would appear on television, and impress audiences by identifying that, for example, 23 October 1901 was a Wednesday. Working out the day of the week from a given date is done by something called modular or clock arithmetic. Maybe the twins discovered that clock arithmetic is also the key to a method that identifies whether a number is prime.

If you take a number, say 17, and calculate 217, then if the remainder when you divide this number by 17 is 2, that is good evidence that the number 17 is prime. This test for primality is often wrongly attributed to the Chinese, and it was the seventeenth-century French mathematician Pierre de Fermat who proved that if the remainder isn’t 2, then that certainly implies that 17 is not prime. In general, if you want to check that p is not a prime, then calculate 2p and divide the result by p. If the remainder isn’t 2, then p can’t be prime. Some people have speculated that, given the twins’ aptitude for identifying days of the week, which depends on a similar technique of looking at remainders on division by 7, they may well have been using this test to find primes.

At first, mathematicians thought that if 2p does have remainder 2 on division by p, then p must be prime. But it turns out that this test does not guarantee primality. 341=31×11 is not prime, yet 2341 has remainder 2 on division by 341. This example was not discovered until 1819, and it is possible that the twins might have been aware of a more sophisticated test that would wheedle out 341. Fermat showed that the test can be extended past powers of 2 by proving that if p is prime, then for any number n less than p, np always has remainder n when divided by the prime p. So if you find any number n for which this fails, you can throw out p as a prime impostor.

For example, 3341 doesn’t have remainder 3 on division by 341—it has remainder 168. The twins couldn’t possibly have been checking through all numbers less than their candidate prime: there would be too many tests for them to run through. However, the great Hungarian prime number wizard Paul Erdos estimated (though he couldn’t prove it rigorously) that to test whether a number less than 10150 is prime, passing Fermat’s test just once means that the chances of the number being not prime are as low as 1 in 1043. So for the twins, probably one test was enough to give them the buzz of prime discovery.

Prime number hopscotch

This is a game for two players in which knowing your twin primes can give you an edge.

Write down the numbers from 1 to 100, or download the prime numbers hopscotch board from The Number Mysteries website. The first player takes a counter and places it on a prime number, which is at most five steps away from square 1. The second player takes the counter and moves it to a bigger prime that is at most five squares ahead of where the first player placed it. The first player follows suit, moving the counter to an even higher prime number which again is at most five squares ahead. The loser is the first player unable to move the counter according to the rules. The rules are: (1) the counter can’t be moved further than five squares ahead, (2) it must always be moved to a prime, and (3) it can’t be moved backwards or left where it is.

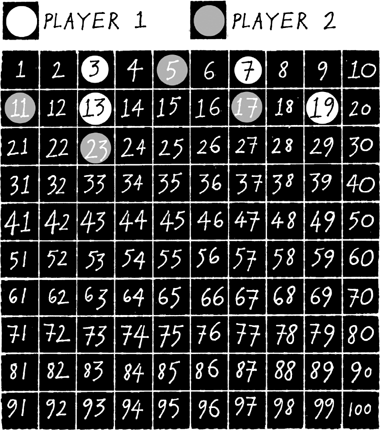
FIGURE 1.21 An example of a prime number hopscotch game where the maximum move is five steps.

The picture above shows a typical scenario. Player 1 has lost the game because the counter is at 23 and there are no primes in the five numbers ahead of 23 which are prime. Could Player 1 have made a better opening move? If you look carefully, you’ll see that once you’ve passed 5 there really aren’t many choices. Whoever moves the counter to 5 is going to win because they will at a later turn be able to move the stone from 19 to 23, leaving their opponent with no prime to move to. So the opening move is vital.

But what if we change the game a little? Let’s say that you are allowed to move the counter to a prime which is at most seven steps ahead. Players can now jump a little further. In particular, they can get past 23 because 29 is six steps ahead and within reach. Does your opening move matter this time? Where will the game end? If you play the game you’ll find that this time you have many more choices along the way, especially when there is a pair of twin primes.

At first sight, with so many choices it looks like your first move is irrelevant. But look again. You lose if you find yourself on 89 because the next prime after 89 is 97, eight steps ahead. If you trace your way back through the primes, you’ll find that being on 67 is crucial because here you get to choose which of the twin primes 71 and 73 you place the counter on. One is a winning choice; the other will lose you the game because every move from that point on is forced on you. Whoever is on 67 can win the game, and it seems that 89 is not so important. So how can you make sure you get there?

If you carry on tracing your way back through the game you’ll find that there’s a crucial decision to be made for anyone on the prime 37. From there, you can reach my daughters’ twin primes, 41 and 43. Move to 41, and you can guarantee winning the game. So now it looks as if the game is decided by whoever can force their opponent to move them to the prime 37. Continuing to wind the game back in this way reveals that there is indeed a winning opening move. Put the counter on 5, and from there you can guarantee that you get all the crucial decisions that ensure you get to move the stone to 89 and win the game because then your opponent can’t move.

What if we continue to make the maximum permitted jump even bigger: can we be always be sure that the game will end? What if we allow each player to move a maximum of 99 steps—can we be sure that the game won’t just go on for ever because you can always jump to another prime within 99 of the last one? After all, we know that there are infinitely many primes, so perhaps at some point you can simply jump from one prime to the next.

It is actually possible to prove that the game does always end. However far you set the maximum jump, there will always be a stretch of numbers greater than the maximum jump containing no primes, and there the game will end. Let’s look at how to find 99 consecutive numbers, none of which is prime. Take the number 100×99×98×97×…×3×2×1. This number is known as 100 factorial, and written as 100! We’re going to use an important fact about this number: if you take any number between 1 and 100, then 100! is divisible by this number.

Look at this sequence of consecutive numbers:

100!+2, 100!+3, 100!+4, …, 100!+98, 100!+99, 100!+100

100!+2 is not prime because it is divisible by 2. Similarly, 100!+3 is not prime because it is divisible by 3. (100! is divisible by 3, so if we add 3 it’s still divisible by 3.) In fact, none of these numbers is prime. Take 100!+53, which is not prime because 100! is divisible by 53, and if we add 53 the result is still divisible by 53. Here are 99 consecutive numbers, none of which is prime. The reason we started at 100!+2 and not 100!+1 is that with this simple method we can deduce only that 100!+1 is divisible by 1, and that won’t help us to tell whether it’s prime. (In fact it isn’t.)

This website has information about where the hopscotch game will end for larger and larger jumps: http://bit.ly/Primehopscotch You can use your smartphone to scan this code.

So we know for certain that if we set the maximum jump to 99, our prime number hopscotch game will end at some point. But 100! is a ridiculously large number. The game actually finished way before this point: the first place where a prime is followed by 99 non-primes is 396,733.

Playing this game certainly reveals the erratic way in which the primes seem to be scattered through the universe of numbers. At first sight there’s no way of knowing where to find the next prime. But if we can’t find a clever device for navigating from one prime to the next, can we at least come up with some clever formulas to produce primes?

Could rabbits and sunflowers be used to find primes?

Count the number of petals on a sunflower. Often there are 89, a prime number. The number of pairs of rabbits after 11 generations is also 89. Have rabbits and flowers discovered some secret formula for finding primes? Not exactly. They like 89 not because it is prime, but because it is one of nature’s other favourite numbers: the Fibonacci numbers. The Italian mathematician Fibonacci of Pisa discovered this important sequence of numbers in 1202 when he was trying to understand the way rabbits multiply (in the biological rather than the mathematical sense).

Fibonacci started by imagining a pair of baby rabbits, one male, one female. Call this starting point month 1. By month 2, these rabbits have matured into an adult pair, which can breed and produce in month 3 a new pair of baby rabbits. (For the purposes of this thought experiment, all litters consist of one male and one female.) In month 4 the first adult pair produce another pair of baby rabbits. Their first pair of baby rabbits has now reached adulthood, so there are now two pairs of adult rabbits and a pair of baby rabbits. In month 5 the two pairs of adult rabbits each produce a pair of baby rabbits. The baby rabbits from month 4 become adults. So by month 5 there are three pairs of adult rabbits and two pairs of baby rabbits, making five pairs of rabbits in total. The number of pairs of rabbits in successive months is given by the following sequence:

FIGURE 1.22 The Fibonacci numbers are the key to calculating the population growth of rabbits.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Keeping track of all these multiplying rabbits was quite a headache until Fibonacci spotted an easy way to work out the numbers. To get the next number in the sequence, you just add the two previous numbers. The bigger of the two is of course the number of pairs of rabbits up to that point. They all survive to the next month, and the smaller of the two is the number of adult pairs. These adult pairs each produce an extra pair of baby rabbits, so the number of rabbits in the next month is the sum of the numbers in the two previous generations.