Logic: Deductive and Inductive

When a Negative term is fully contradictory of its Positive it is said to be Infinite; because it denotes an unascertained multitude of things, a multitude only limited by the positive term and the suppositio; thus 'not-wise' denotes all except the wise, within the suppositio of 'intelligent beings.' Formally (disregarding any suppositio), such a negative term stands for all possible terms except its positive: x denotes everything but X; and 'not-wise' may be taken to include stones, triangles and hippogriffs. And even in this sense, a negative term has some positive meaning, though a very indefinite one, not a specific positive force like 'unwise' or 'unhappy': it denotes any and everything that has not the attributes connoted by the corresponding positive term.

Privative Terms connote the absence of a quality that normally belongs to the kind of thing denoted, as 'blind' or 'deaf.' We may predicate 'blind' or 'deaf' of a man, dog or cow that happens not to be able to see or hear, because the powers of seeing and hearing generally belong to those species; but of a stone or idol these terms can only be used figuratively. Indeed, since the contradictory of a privative carries with it the privative limitation, a stone is strictly 'not-blind': that is, it is 'not-something-that-normally-having-sight-wants-it.'

Contrary Terms are those that (within a certain genus or suppositio) severally connote differential qualities that are, in fact, mutually incompatible in the same relation to the same thing, and therefore cannot be predicated of the same subject in the same relation; and, so far, they resemble Contradictory Terms: but they differ from contradictory terms in this, that the differential quality connoted by each of them is definitely positive; no Contrary Term is infinite, but is limited to part of the suppositio excluded by the others; so that, possibly, neither of two Contraries is truly predicable of a given subject. Thus 'blue' and 'red' are Contraries, for they cannot both be predicated of the same thing in the same relation; but are not Contradictories, since, in a given case, neither may be predicable: if a flower is blue in a certain part, it cannot in the same part be red; but it may be neither blue nor red, but yellow; though it is certainly either blue or not-blue. All co-ordinate terms are formal Contraries; but if, in fact, a series of co-ordinates comprises only two (as male-female), they are empirical Contradictories; since each includes all that area of the suppositio which the other excludes.

The extremes of a series of co-ordinate terms are Opposites; as, in a list of colours, white and black, the most strongly contrasted, are said to be opposites, or as among moods of feeling, rapture and misery are opposites. But this distinction is of slight logical importance. Imperfect Positive and Negative couples, like 'happy and unhappy,' which (as we have seen) are not contradictories, are often called Opposites.

The members of any series of Contraries are all included by any one of them and its contradictory, as all colours come under 'red' and 'not-red,' all moods of feeling under 'happy' and 'not-happy.'

CHAPTER V

THE CLASSIFICATION OF PROPOSITIONS

§ 1. Logicians classify Propositions according to Quantity, Quality, Relation and Modality.

As to Quantity, propositions are either Universal or Particular; that is to say, the predicate is affirmed or denied either of the whole subject or of a part of it—of All or of Some S.

All S is P (that is, P is predicated of all S).

Some S is P (that is, P is predicated of some S).

An Universal Proposition may have for its subject a singular term, a collective, a general term distributed, or an abstract term.

(1) A proposition having a singular term for its subject, as The Queen has gone to France, is called a Singular Proposition; and some Logicians regard this as a third species of proposition with respect to quantity, distinct from the Universal and Particular; but that is needless.

(2) A collective term may be the subject, as The Black Watch is ordered to India. In this case, as well as in singular propositions, a predication is made concerning the whole subject as a whole.

(3) The subject may be a general term taken in its full denotation, as All apes are sagacious; and in this case a Predication is made concerning the whole subject distributively; that is, of each and everything the subject stands for.

(4) Propositions whose subjects are abstract terms, though they may seem to be formally Singular, are really as to their meaning distributive Universals; since whatever is true of a quality is true of whatever thing has that quality so far as that quality is concerned. Truth will prevail means that All true propositions are accepted at last (by sheer force of being true, in spite of interests, prejudices, ignorance and indifference). To bear this in mind may make one cautious in the use of abstract terms.

In the above paragraphs a distinction is implied between Singular and Distributive Universals; but, technically, every term, whether subject or predicate, when taken in its full denotation (or universally), is said to be 'distributed,' although this word, in its ordinary sense, would be directly applicable only to general terms. In the above examples, then, 'Queen,' 'Black Watch,' 'apes,' and 'truth' are all distributed terms. Indeed, a simple definition of the Universal Proposition is 'one whose subject is distributed.'

A Particular Proposition is one that has a general term for its subject, whilst its predicate is not affirmed or denied of everything the subject denotes; in other words, it is one whose subject is not distributed: as Some lions inhabit Africa.

In ordinary discourse it is not always explicitly stated whether predication is universal or particular; it would be very natural to say Lions inhabit Africa, leaving it, as far as the words go, uncertain whether we mean all or some lions. Propositions whose quantity is thus left indefinite are technically called 'preindesignate,' their quantity not being stated or designated by any introductory expression; whilst propositions whose quantity is expressed, as All foundling-hospitals have a high death-rate, or Some wine is made from grapes, are said to be 'predesignate.' Now, the rule is that preindesignate propositions are, for logical purposes, to be treated as particular; since it is an obvious precaution of the science of proof, in any practical application, not to go beyond the evidence. Still, the rule may be relaxed if the universal quantity of a preindesignate proposition is well known or admitted, as in Planets shine with reflected light—understood of the planets of our solar system at the present time. Again, such a proposition as Man is the paragon of animals is not a preindesignate, but an abstract proposition; the subject being elliptical for Man according to his proper nature; and the translation of it into a predesignate proposition is not All men are paragons; nor can Some men be sufficient, since an abstract can only be adequately rendered by a distributed term; but we must say, All men who approach the ideal. Universal real propositions, true without qualification, are very scarce; and we often substitute for them general propositions, saying perhaps—generally, though not universally, S is P. Such general propositions are, in strictness, particular; and the logical rules concerning universals cannot be applied to them without careful scrutiny of the facts.

The marks or predesignations of Quantity commonly used in Logic are: for Universals, All, Any, Every, Whatever (in the negative No or No one, see next §); for Particulars, Some.

Now Some, technically used, does not mean Some only, but Some at least (it may be one, or more, or all). If it meant 'Some only,' every particular proposition would be an exclusive exponible (chap. ii. § 3); since Only some men are wise implies that Some men are not wise. Besides, it may often happen in an investigation that all the instances we have observed come under a certain rule, though we do not yet feel justified in regarding the rule as universal; and this situation is exactly met by the expression Some (it may be all).

The words Many, Most, Few are generally interpreted to mean Some; but as Most signifies that exceptions are known, and Few that the exceptions are the more numerous, propositions thus predesignate are in fact exponibles, mounting to Some are and Some are not. If to work with both forms be too cumbrous, so that we must choose one, apparently Few are should be treated as Some are not. The scientific course to adopt with propositions predesignate by Most or Few, is to collect statistics and determine the percentage; thus, Few men are wise—say 2 per cent.

The Quantity of a proposition, then, is usually determined entirely by the quantity of the subject, whether all or some. Still, the quantity of the predicate is often an important consideration; and though in ordinary usage the predicate is seldom predesignate, Logicians agree that in every Negative Proposition (see § 2) the predicate is 'distributed,' that is to say, is denied altogether of the subject, and that this is involved in the form of denial. To say Some men are not brave, is to declare that the quality for which men may be called brave is not found in any of the Some men referred to: and to say No men are proof against flattery, cuts off the being 'proof against flattery' entirely from the list of human attributes. On the other hand, every Affirmative Proposition is regarded as having an undistributed predicate; that is to say, its predicate is not affirmed exclusively of the subject. Some men are wise does not mean that 'wise' cannot be predicated of any other beings; it is equivalent to Some men are wise (whoever else may be). And All elephants are sagacious does not limit sagacity to elephants: regarding 'sagacious' as possibly denoting many animals of many species that exhibit the quality, this proposition is equivalent to 'All elephants are some sagacious animals.' The affirmative predication of a quality does not imply exclusive possession of it as denial implies its complete absence; and, therefore, to regard the predicate of an affirmative proposition as distributed would be to go beyond the evidence and to take for granted what had never been alleged.

Some Logicians, seeing that the quantity of predicates, though not distinctly expressed, is recognised, and holding that it is the part of Logic "to make explicit in language whatever is implicit in thought," have proposed to exhibit the quantity of predicates by predesignation, thus: 'Some men are some wise (beings)'; 'some men are not any brave (beings)'; etc. This is called the Quantification of the Predicate, and leads to some modifications of Deductive Logic which will be referred to hereafter. (See § 5; chap. vii. § 4, and chap. viii. § 3.)

§ 2. As to Quality, Propositions are either Affirmative or Negative. An Affirmative Proposition is, formally, one whose copula is affirmative (or, has no negative sign), as S—is—P, All men—are—partial to themselves. A Negative Proposition is one whose copula is negative (or, has a negative sign), as S—is not—P, Some men—are not—proof against flattery. When, indeed, a Negative Proposition is of Universal Quantity, it is stated thus: No S is P, No men are proof against flattery; but, in this case, the detachment of the negative sign from the copula and its association with the subject is merely an accident of our idiom; the proposition is the same as All men—are not—proof against flattery. It must be distinguished, therefore, from such an expression as Not every man is proof against flattery; for here the negative sign really restricts the subject; so that the meaning is—Some men at most (it may be none) are proof against flattery; and thus the proposition is Particular, and is rendered—Some men—are not—proof against flattery.

When the negative sign is associated with the predicate, so as to make this an Infinite Term (chap. iv. § 8), the proposition is called an Infinite Proposition, as S is not-P (or p), All men are—incapable of resisting flattery, or are—not-proof against flattery.

Infinite propositions, when the copula is affirmative, are formally, themselves affirmative, although their force is chiefly negative; for, as the last example shows, the difference between an infinite and a negative proposition may depend upon a hyphen. It has been proposed, indeed, with a view to superficial simplification, to turn all Negatives into Infinites, and thus render all propositions Affirmative in Quality. But although every proposition both affirms and denies something according to the aspect in which you regard it (as Snow is white denies that it is any other colour, and Snow is not blue affirms that it is some other colour), yet there is a great difference between the definite affirmation of a genuine affirmative and the vague affirmation of a negative or infinite; so that materially an affirmative infinite is the same as a negative.

Generally Mill's remark is true, that affirmation and denial stand for distinctions of fact that cannot be got rid of by manipulation of words. Whether granite sinks in water, or not; whether the rook lives a hundred years, or not; whether a man has a hundred dollars in his pocket, or not; whether human bones have ever been found in Pliocene strata, or not; such alternatives require distinct forms of expression. At the same time, it may be granted that many facts admit of being stated with nearly equal propriety in either Quality, as No man is proof against flattery, or All men are open to flattery.

But whatever advantage there is in occasionally changing the Quality of a proposition may be gained by the process of Obversion (chap. vii. § 5); whilst to use only one Quality would impair the elasticity of logical expression. It is a postulate of Logic that the negative sign may be transferred from the copula to the predicate, or from the predicate to the copula, without altering the sense of a proposition; and this is justified by the experience that not to have an attribute and to be without it are the same thing.

§ 3. A. I. E. O.—Combining the two kinds of Quantity, Universal and Particular, with the two kinds of Quality, Affirmative and Negative, we get four simple types of proposition, which it is usual to symbolise by the letters A. I. E. O., thus:

As an aid to the remembering of these symbols we may observe that A. and I. are the first two vowels in affirmo and that E. and O. are the vowels in nego.

It must be acknowledged that these four kinds of proposition recognised by Formal Logic constitute a very meagre selection from the list of propositions actually used in judgment and reasoning.

Those Logicians who explicitly quantify the predicate obtain, in all, eight forms of proposition according to Quantity and Quality:

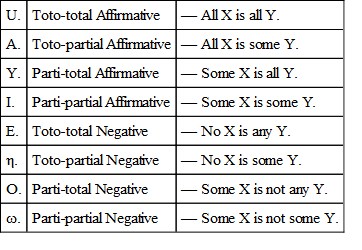
Here A. I. E. O. correspond with those similarly symbolised in the usual list, merely designating in the predicates the quantity which was formerly treated as implicit.

§ 4. As to Relation, propositions are either Categorical or Conditional. A Categorical Proposition is one in which the predicate is directly affirmed or denied of the subject without any limitation of time, place, or circumstance, extraneous to the subject, as All men in England are secure of justice; in which proposition, though there is a limitation of place ('in England'), it is included in the subject. Of this kind are nearly all the examples that have yet been given, according to the form S is P.

A Conditional Proposition is so called because the predication is made under some limitation or condition not included in the subject, as If a man live in England, he is secure of justice. Here the limitation 'living in England' is put into a conditional sentence extraneous to the subject, 'he,' representing any man.

Conditional propositions, again, are of two kinds—Hypothetical and Disjunctive. Hypothetical propositions are those that are limited by an explicit conditional sentence, as above, or thus: If Joe Smith was a prophet, his followers have been unjustly persecuted. Or in symbols thus:

If A is, B is;

If A is B, A is C;

If A is B, C is D.

Disjunctive propositions are those in which the condition under which predication is made is not explicit but only implied under the disguise of an alternative proposition, as Joe Smith was either a prophet or an impostor. Here there is no direct predication concerning Joe Smith, but only a predication of one of the alternatives conditionally on the other being denied, as, If Joe Smith was not a prophet he was an impostor; or, If he was not an impostor, he was a prophet. Symbolically, Disjunctives may be represented thus:

A is either B or C,

Either A is B or C is D.

Formally, every Conditional may be expressed as a Categorical. For our last example shows how a Disjunctive may be reduced to two Hypotheticals (of which one is redundant, being the contrapositive of the other; see chap. vii. § 10). And a Hypothetical is reducible to a Categorical thus: If the sky is clear, the night is cold may be read—The case of the sky being clear is a case of the night being cold; and this, though a clumsy plan, is sometimes convenient. It would be better to say The sky being clear is a sign of the night being cold, or a condition of it. For, as Mill says, the essence of a Hypothetical is to state that one clause of it (the indicative) may be inferred from the other (the conditional). Similarly, we might write: Proof of Joe Smith's not being a prophet is a proof of his being an impostor.

This turning of Conditionals into Categoricals is called a Change of Relation; and the process may be reversed: All the wise are virtuous may be written, If any man is wise he is virtuous; or, again, Either a man is not-wise or he is virtuous. But the categorical form is usually the simplest.

If, then, as substitutes for the corresponding conditionals, categoricals are formally adequate, though sometimes inelegant, it may be urged that Logic has nothing to do with elegance; or that, at any rate, the chief elegance of science is economy, and that therefore, for scientific purposes, whatever we may write further about conditionals must be an ugly excrescence. The scientific purpose of Logic is to assign the conditions of proof. Can we, then, in the conditional form prove anything that cannot be proved in the categorical? Or does a conditional require to be itself proved by any method not applicable to the Categorical? If not, why go on with the discussion of Conditionals? For all laws of Nature, however stated, are essentially categorical. 'If a straight line falls on another straight line, the adjacent angles are together equal to two right angles'; 'If a body is unsupported, it falls'; 'If population increases, rents tend to rise': here 'if' means 'whenever' or 'all cases in which'; for to raise a doubt whether a straight line is ever conceived to fall upon another, whether bodies are ever unsupported, or population ever increases, is a superfluity of scepticism; and plainly the hypothetical form has nothing to do with the proof of such propositions, nor with inference from them.

Still, the disjunctive form is necessary in setting out the relation of contradictory terms, and in stating a Division (chap. xxi.), whether formal (as A is B or not-B) or material (as Cats are white, or black, or tortoiseshell, or tabby). And in some cases the hypothetical form is useful. One of these occurs where it is important to draw attention to the condition, as something doubtful or especially requiring examination. If there is a resisting medium in space, the earth will fall into the sun; If the Corn Laws are to be re-enacted, we had better sell railways and buy land: here the hypothetical form draws attention to the questions whether there is a resisting medium in space, whether the Corn Laws are likely to be re-enacted; but as to methods of inference and proof, the hypothetical form has nothing to do with them. The propositions predicate causation: A resisting medium in space is a condition of the earth's falling into the sun; A Corn Law is a condition of the rise of rents, and of the fall of railway profits.

A second case in which the hypothetical is a specially appropriate form of statement occurs where a proposition relates to a particular matter and to future time, as If there be a storm to-morrow, we shall miss our picnic. Such cases are of very slight logical interest. It is as exercises in formal thinking that hypotheticals are of most value; inasmuch as many people find them more difficult than categoricals to manipulate.

In discussing Conditional Propositions, the conditional sentence of a Hypothetical, or the first alternative of a Disjunctive, is called the Antecedent; the indicative sentence of a Hypothetical, or the second alternative of a Disjunctive, is called the Consequent.

Hypotheticals, like Categoricals, have been classed according to Quantity and Quality. Premising that the quantity of a Hypothetical depends on the quantity of its Antecedent (which determines its limitation), whilst its quality depends on the quality of its consequent (which makes the predication), we may exhibit four forms:

A. If A is B, C is D;

I. Sometimes when A is B, C is D;

E. If A is B, C is not D;

O. Sometimes when A is B, C is not D.

But I. and O. are rarely used.

As for Disjunctives, it is easy to distinguish the two quantities thus:

A. Either A is B, or C is D;

I. Sometimes either A is B or C is D.

But I. is rarely used. The distinction of quality, however, cannot be made: there are no true negative forms; for if we write—

Neither is A B, nor C D,

there is here no alternative predication, but only an Exponible equivalent to No A is B, and No C is D. And if we write—

Either A is not B, or C is not D,

this is affirmative as to the alternation, and is for all methods of treatment equivalent to A.

Logicians are divided in opinion as to the interpretation of the conjunction 'either, or'; some holding that it means 'not both,' others that it means 'it may be both.' Grammatical usage, upon which the question is sometimes argued, does not seem to be established in favour of either view. If we say A man so precise in his walk and conversation is either a saint or a consummate hypocrite; or, again, One who is happy in a solitary life is either more or less than man; we cannot in such cases mean that the subject may be both. On the other hand, if it be said that the author of 'A Tale of a Tub' is either a misanthrope or a dyspeptic, the alternatives are not incompatible. Or, again, given that X. is a lunatic, or a lover, or a poet, the three predicates have much congruity.

It has been urged that in Logic, language should be made as exact and definite as possible, and that this requires the exclusive interpretation 'not both.' But it seems a better argument, that Logic (1) should be able to express all meanings, and (2), as the science of evidence, must not assume more than is given; to be on the safe side, it must in doubtful cases assume the least, just as it generally assumes a preindesignate term to be of particular quantity; and, therefore 'either, or' means 'one, or the other, or both.'