Logic: Deductive and Inductive

§ 6. These considerations have an important bearing upon the interpretation of probabilities. The average probability for any general class or series of events cannot be confidently applied to any one instance or to any special class of instances, since this one, or this special class, may exhibit a striking error or deviation; it may, in fact, be subject to special causes. Within the class whose average is first taken, and which is described by general characters as 'a man,' or 'a die,' or 'a rifle shot,' there may be classes marked by special characters and determined by special influences. Statistics giving the average for 'mankind' may not be true of 'civilised men,' or of any still smaller class such as 'Frenchmen.' Hence life-insurance offices rely not merely on statistics of life and death in general, but collect special evidence in respect of different ages and sexes, and make further allowance for teetotalism, inherited disease, etc. Similarly with individual cases: the average expectation for a class, whether general or special, is only applicable to any particular case if that case is adequately described by the class characters. In England, for example, the average expectation of life for males at 20 years of age is 39.40; but at 60 it is still 13.14, and at 73 it is 7.07; at 100 it's 1.61. Of men 20 years old those who live more or less than 39.40 years are deviations or errors; but there are a great many of them. To insure the life of a single man at 20, in the expectation of his dying at 60, would be a mere bet, if we had no special knowledge of him; the safety of an insurance office lies in having so many clients that opposite deviations cancel one another: the more clients the safer the business. It is quite possible that a hundred men aged 20 should be insured in one week and all of them die before 25; this would be ruinous, if others did not live to be 80 or 90.

Not only in such a practical affair as insurance, but in matters purely scientific, the minute and subtle peculiarities of individuals have important consequences. Each man has a certain cast of mind, character, physique, giving a distinctive turn to all his actions even when he tries to be normal. In every employment this determines his Personal Equation, or average deviation from the normal. The term Personal Equation is used chiefly in connection with scientific observation, as in Astronomy. Each observer is liable to be a little wrong, and this error has to be allowed for and his observations corrected accordingly.

The use of the term 'expectation,' and of examples drawn from insurance and gambling, may convey the notion that probability relates entirely to future events; but if based on laws and causes, it can have no reference to point of time. As long as conditions are the same, events will be the same, whether we consider uniformities or averages. We may therefore draw probable inferences concerning the past as well as the future, subject to the same hypothesis, that the causes affecting the events in question were the same and similarly combined. On the other hand, if we know that conditions bearing on the subject of investigation, have changed since statistics were collected, or were different at some time previous to the collection of evidence, every probable inference based on those statistics must be corrected by allowing for the altered conditions, whether we desire to reason forwards or backwards in time.

§ 7. The rules for the combination of probabilities are as follows:

(1) If two events or causes do not concur, the probability of one or the other occurring is the sum of the separate probabilities. A die cannot turn up both ace and six; but the probability in favour of each is 1/6: therefore, the probability in favour of one or the other is 1/3. Death can hardly occur from both burning and drowning: if 1 in 1000 is burned and 2 in 1000 are drowned, the probability of being burned or drowned is 3/1000.

(2) If two events are independent, having neither connection nor repugnance, the probability of their concurring is found by multiplying together the separate probabilities of each occurring. If in walking down a certain street I meet A once in four times, and B once in three times, I ought (by mere chance) to meet both once in twelve times: for in twelve occasions I meet B four times; but once in four I meet A.

This is a very important rule in scientific investigation, since it enables us to detect the presence of causation. For if the coincidence of two events is more or less frequent than it would be if they were entirely independent, there is either connection or repugnance between them. If, e.g., in walking down the street I meet both A and B oftener than once in twelve times, they may be engaged in similar business, calling them from their offices at about the same hour. If I meet them both less often than once in twelve times, they may belong to the same office, where one acts as a substitute for the other. Similarly, if in a multitude of throws a die turns six oftener than once in six times, it is not a fair one: that is, there is a cause favouring the turning of six. If of 20,000 people 500 see apparitions and 100 have friends murdered, the chance of any man having both experiences is 1/8000; but if each lives on the average 300,000 hours, the chance of both events occurring in the same hour is 1/2400000000. If the two events occur in the same hour oftener than this, there is more than a chance coincidence.

The more minute a cause of connection or repugnance between events, the longer the series of trials or instances necessary to bring out its influence: the less a die is loaded, the more casts must be made before it can be shown that a certain side tends to recur oftener than once in six.

(3) The rule for calculating the probability of a dependent event is the same as the above; for the concurrence of two independent events is itself dependent upon each of them occurring. My meeting with both A and B in the street is dependent on my walking there and on my meeting one of them. Similarly, if A is sometimes a cause of B (though liable to be frustrated), and B sometimes of C (C and B having no causes independent of B and A respectively), the occurrence of C is dependent on that of B, and that again on the occurrence of A. Hence we may state the rule: If two events are dependent each on another, so that if one occur the second may (or may not), and if the second a third; whilst the third never occurs without the second, nor the second without the first; the probability that if the first occur the third will, is found by multiplying together the fractions expressing the probability that the first is a mark of the second and the second of the third.

Upon this principle the value of hearsay evidence or tradition deteriorates, and generally the cogency of any argument based upon the combination of approximate generalisations dependent on one another or "self-infirmative." If there are two witnesses, A and B, of whom A saw an event, whilst B only heard A relate it (and is therefore dependent on A), what credit is due to B's recital? Suppose the probability of each man's being correct as to what he says he saw, or heard, is 3/4: then (3/4 × 3/4 = 9/16) the probability that B's story is true is a little more than 1/2. For if in 16 attestations A is wrong 4 times, B can only be right in 3/4 of the remainder, or 9 times in 16. Again, if we have the Approximate Generalisations, 'Most attempts to reduce wages are met by strikes,' and 'Most strikes are successful,' and learn, on statistical inquiry, that in every hundred attempts to reduce wages there are 80 strikes, and that 70 p.c. of the strikes are successful, then 56 p.c. of attempts to reduce wages are unsuccessful.

Of course this method of calculation cannot be quantitatively applied if no statistics are obtainable, as in the testimony of witnesses; and even if an average numerical value could be attached to the evidence of a certain class of witnesses, it would be absurd to apply it to the evidence of any particular member of the class without taking account of his education, interest in the case, prejudice, or general capacity. Still, the numerical illustration of the rapid deterioration of hearsay evidence, when less than quite veracious, puts us on our guard against rumour. To retail rumour may be as bad as to invent an original lie.

(4) If an event may coincide with two or more other independent events, the probability that they will together be a sign of it, is found by multiplying together the fractions representing the improbability that each is a sign of it, and subtracting the product from unity.

This is the rule for estimating the cogency of circumstantial evidence and analogical evidence; or, generally, for combining approximate generalisations "self-corroboratively." If, for example, each of two independent circumstances, A and B, indicates a probability of 6 to 1 in favour of a certain event; taking 1 to represent certainty, 1-6/7 is the improbability of the event, notwithstanding each circumstance. Then 1/7 × 1/7 = 1/49, the improbability of both proving it. Therefore the probability of the event is 48 to 1. The matter may be plainer if put thus: A's indication is right 6 times in 7, or 42 in 49; in the remaining 7 times in 49, B's indication will be right 6 times. Therefore, together they will be right 48 times in 49. If each of two witnesses is truthful 6 times in 7, one or the other will be truthful 48 times in 49. But they will not be believed unless they agree; and in the 42 cases of A being right, B will contradict him 6 times; so that they only concur in being right 36 times. In the remaining 7 times in which A is wrong, B will contradict him 6 times, and once they will both be wrong. It does not follow that when both are wrong they will concur; for they may tell very different stories and still contradict one another.

If in an analogical argument there were 8 points of comparison, 5 for and 3 against a certain inference, and the probability raised by each point could be quantified, the total value of the evidence might be estimated by doing similar sums for and against, and subtracting the unfavourable from the favourable total.

When approximate generalisations that have not been precisely quantified combine their evidence, the cogency of the argument increases in the same way, though it cannot be made so definite. If it be true that most poets are irritable, and also that most invalids are irritable, a still greater proportion will be irritable of those who are both invalids and poets.

On the whole, from the discussion of probabilities there emerge four principal cautions as to their use: Not to make a pedantic parade of numerical probability, where the numbers have not been ascertained; Not to trust to our feeling of what is likely, if statistics can be obtained; Not to apply an average probability to special classes or individuals without inquiring whether they correspond to the average type; and Not to trust to the empirical probability of events, if their causes can be discovered and made the basis of reasoning which the empirical probability may be used to verify.

The reader who wishes to pursue this subject further should read a work to which the foregoing chapter is greatly indebted, Dr. Venn's Logic of Chance.

CHAPTER XXI

DIVISION AND CLASSIFICATION

§ 1. Classification, in its widest sense, is a mental grouping of facts or phenomena according to their resemblances and differences, so as best to serve some purpose. A "mental grouping": for although in museums we often see the things themselves arranged in classes, yet such an arrangement only contains specimens representing a classification. The classification itself may extend to innumerable objects most of which have never been seen at all. Extinct animals, for example, are classified from what we know of their fossils; and some of the fossils may be seen arranged in a museum; but the animals themselves have disappeared for many ages.

Again, things are classed according to their resemblances and differences: that is to say, those that most closely resemble one another are classed together on that ground; and those that differ from one another in important ways, are distributed into other classes. The more the things differ, the wider apart are their classes both in thought and in the arrangements of a museum. If their differences are very great, as with animals, vegetables and minerals, the classing of them falls to different departments of thought or science, and is often represented in different museums, zoological, botanical, mineralogical.

We must not, however, suppose that there is only one way of classifying things. The same objects may be classed in various ways according to the purpose in view. For gardening, we are usually content to classify plants into trees, shrubs, flowers, grasses and weeds; the ordinary crops of English agriculture are distinguished, in settling their rotation, into white and green; the botanist divides the higher plants into gymnosperms and angiosperms, and the latter into monocotyledons and dicotyledons. The principle of resemblance and difference is recognised in all these cases; but what resemblances or differences are important depends upon the purpose to be served.

Purposes are either (α) special or practical, as in gardening or hunting, or (β) general or scientific, as in Botany or Zoology. The scientific purpose is merely knowledge; it may indeed subserve all particular or practical ends, but has no other end than knowledge directly in view. And whilst, even for knowledge, different classifications may be suitable for different lines of inquiry, in Botany and Zoology the Morphological Classification is that which gives the most general and comprehensive knowledge (see Huxley, On the Classification of Animals, ch. 1). Most of what a logician says about classification is applicable to the practical kind; but the scientific (often called 'Natural Classification'), as the most thorough and comprehensive, is what he keeps most constantly before him.

Scientific classification comes late in human history, and at first works over earlier classifications which have been made by the growth of intelligence, of language, and of the practical arts. Even in the distinctions recognised by animals, may be traced the grounds of classification: a cat does not confound a dog with one of its own species, nor water with milk, nor cabbage with fish. But it is in the development of language that the progress of instinctive classification may best be seen. The use of general names implies the recognition of classes of things corresponding to them, which form their denotation, and whose resembling qualities, so far as recognised, form their connotation; and such names are of many degrees of generality. The use of abstract names shows that the objects classed have also been analysed, and that their resembling qualities have been recognised amidst diverse groups of qualities.

Of the classes marked by popular language it is worth while to distinguish two sorts (cf. chap. xix. § 4): Kinds, and those having but few points of agreement.

But the popular classifications, made by language and the primitive arts, are very imperfect. They omit innumerable things which have not been found useful or noxious, or have been inconspicuous, or have not happened to occur in the region inhabited by those who speak a particular language; and even things recognised and named may have been very superficially examined, and therefore wrongly classed, as when a whale or porpoise is called a fish, or a slowworm is confounded with snakes. A scientific classification, on the other hand, aims at the utmost comprehensiveness, ransacking the whole world from the depths of the earth to the remotest star for new objects, and scrutinising everything with the aid of crucible and dissecting knife, microscope and spectroscope, to find the qualities and constitution of everything, in order that it may be classed among those things with which it has most in common and distinguished from those other things from which it differs. A scientific classification continually grows more comprehensive, more discriminative, more definitely and systematically coherent. Hence the uses of classification may be easily perceived.

§ 2. The first use of classification is the better understanding of the facts of Nature (or of any sphere of practice); for understanding consists in perceiving and comprehending the likeness and difference of things, in assimilating and distinguishing them; and, in carrying out this process systematically, new correlations of properties are continually disclosed. Thus classification is closely analogous to explanation. Explanation has been shown (chap. xix. § 5) to consist in the discovery of the laws or causes of changes in Nature; and laws and causes imply similarity, or like changes under like conditions: in the same way classification consists in the discovery of resemblances in the things that undergo change. We may say (subject to subsequent qualifications) that Explanation deals with Nature in its dynamic, Classification in its static aspect. In both cases we have a feeling of relief. When the cause of any event is pointed out, or an object is assigned its place in a system of classes, the gaping wonder, or confusion, or perplexity, occasioned by an unintelligible thing, or by a multitude of such things, is dissipated. Some people are more than others susceptible of this pleasure and fastidious about its purity.

A second use of classification is to aid the memory. It strengthens memory, because one of the conditions of our recollecting things is, that they resemble what we last thought of; so that to be accustomed to study and think of things in classes must greatly facilitate recollection. But, besides this, a classification enables us easily to run over all the contrasted and related things that we want to think of. Explanation and classification both tend to rationalise the memory, and to organise the mind in correspondence with Nature.

Every one knows how a poor mind is always repeating itself, going by rote through the same train of words, ideas, actions; and that such a mind is neither interesting nor practical. It is not practical, because the circumstances of life are rarely exactly repeated, so that for a present purpose it is rarely enough to remember only one former case; we need several, that by comparing (perhaps automatically) their resemblances and differences with the one before us, we may select a course of action, or a principle, or a parallel, suited to our immediate needs. Greater fertility and flexibility of thought seem naturally to result from the practice of explanation and classification. But it must be honestly added, that the result depends upon the spirit in which such study is carried on; for if we are too fond of finality, too eager to believe that we have already attained a greater precision and comprehension than are in fact attainable, nothing can be more petrific than 'science,' and our last state may be worse than the first. Of this, students of Logic have often furnished examples.

§ 3. Classification may be either Deductive or Inductive; that is to say, in the formation of classes, as in the proof of propositions, we may, on the whole, proceed from the more to the less, or from the less to the more general; not that these two processes are entirely independent.

If we begin with some large class, such as 'Animal,' and subdivide it deductively into Vertebrate and Invertebrate, yet the principle of division (namely, central structure) has first been reached by a comparison of examples and by generalisation; if, on the other hand, beginning with individuals, we group them inductively into classes, and these again into wider ones (as dogs, rats, horses, whales and monkeys into mammalia) we are guided both in special cases by hypotheses as to the best grounds of resemblance, and throughout by the general principle of classification—to associate things that are alike and to separate things that are unlike. This principle holds implicitly a place in classification similar to that of causation in explanation; both are principles of intelligence. Here, then, as in proof, induction is implied in deduction, and deduction in induction. Still, the two modes of procedure may be usefully distinguished: in deduction, we proceed from the idea of a whole to its parts, from general to special; in induction, from special (or particular) to general, from parts to the idea of a whole.

§ 4. The process of Deductive Classification, or Formal Division, may be represented thus:

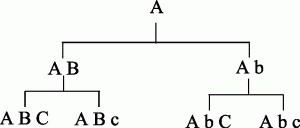
Given any class (A) to be divided:

1. Select one important character, attribute, or quality (B), not common to all the individuals comprehended in the class, as the basis of division (fundamentum divisionis).

2. Proceed by Dichotomy; that is, cut the given class into two, one having the selected attribute (say, B), the other not having it (b). This, like all formal processes, assumes the principles of Contradiction and Excluded Middle, that 'No A is both B and not-B,' and that 'Every A is either B or not-B' (chap. vi. § 3); and if these principles are not true, or not applicable, the method fails.

When a class is thus subdivided, it may be called, in relation to its subclasses, a Genus; and in relation to it, the subclasses may be called Species: thus—genus A, species AB and Ab, etc.

3. Proceed gradually in the order of the importance of characters; that is, having divided the given class, subdivide on the same principle the two classes thence arising; and so again and again, step by step, until all the characters are exhausted: Divisio ne fiat per saltum.

Suppose we were to attempt an exhaustive classification of things by this method, we must begin with 'All Things,' and divide them (say) into phenomenal and not-phenomenal, and then subdivide phenomena, and so on, thus:

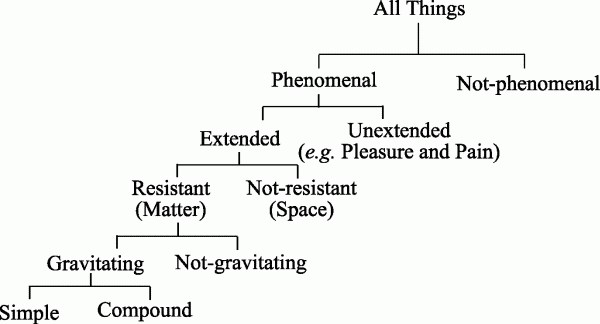
Having subdivided 'Simple' by all possible characters, we must then go back and similarly subdivide Not-phenomenal, Unextended, Not-resistant, Not-gravitating, and Compound. Now, if we knew all possible characters, and the order of their importance, we might prepare a priori a classification of all possible things; at least, of all things that come under the principles of Contradiction and Excluded Middle. Many of our compartments might contain nothing actual; there may, for example, be nothing that is not phenomenal to some mind, or nothing that is extended and not-resistant (no vacuum), and so forth. This would imply a breach of the rule, that the dividing quality be not common to the whole class; but, in fact, doubts have been, and are, seriously entertained whether these compartments are filled or not. If they are not, we have concepts representing nothing, which have been generated by the mere force of grammatical negation, or by the habit of thinking according to the principle of Excluded Middle; and, on the strength of these empty concepts, we have been misled into dividing by an attribute, which (being universal) cannot be a fundamentum divisionis. But though in such a classification places might be empty, there would be a place for everything; for whatever did not come into some positive class (such as Gravitating) must fall under one of the negative classes (the 'Nots') that run down the right-hand side of the Table and of its subdivisions.

This is the ideal of classification. Unfortunately we have to learn what characters or attributes are possible, by experience and comparison; we are far from knowing them all: and we do not know the order of their importance; nor are we even clear what 'important' means in this context, whether 'widely prevalent,' or 'ancient,' or 'causally influential,' or 'indicative of others.' Hence, in classifying actual things, we must follow the inductive method of beginning with particulars, and sorting them according to their likeness and difference as discovered by investigation. The exceptional cases, in which deduction is really useful, occur where certain limits to the number and combination of qualities happen to be known, as they may be in human institutions, or where there are mathematical conditions. Thus, we might be able to classify orders of Architecture, or the classical metres and stanzas of English poetry; though, in fact, these things are too free, subtle and complex for deductive treatment: for do not the Arts grow like trees? The only sure cases are mathematical; as we may show that there are possible only three kinds of plane triangles, four conic sections, five regular solids.