Извлеченные скрытые знания: когнитивные модели

Остальные 3 z-фактоа с меньшей силой выражают негативную характеристику соцлен-руководителя, подверженного социальной лени в рамках исходных 6 смыслов z-факторов, сформулированных Рингельманом.

Результаты осмысления 3-х y—переменных y4, y5, y6, остальные смысловые уравнения для смыслов y—переменных y1, y2, y3 не имеют решений, эти случаи отсутствия решении такие же, что и в предметных областях статей [1—11,30,33,34].

Результаты осмысления 3-х y—переменных y4, y5, y6 приведены в Таблице 5.3. В левой колонке Таблицы 5.3 приведены имена-смысли z—изменчивостей, в правой – «веса» ckj z-изменчивостей, с учетом значений которых конструировались фразы смыслов y—переменных y4, y5, y6. Если подставить значения zik z—изменчивости и значение ckj в формулу y—изменчивости yij, то, просуммировав полученные произведения k=1,…,6, получим одно (i,j) -ое значение y—изменчивости.

Дисперсии Λ66=diag (2.4441,1.7629,1.7629, 0.0100,0.0100,0.0100) измеряют доли количеств информации для 6 ситуаций, одновременно элементы Λ66 равны дисперсиям y—изменчивости для ситуации №4,№5,№6 Этот числовой факт интерпретируем словесно: количество информации об y-изменчивости в 3-х ситуациях равны друг другу и практически равны 0.

Таблица 5.3.Выявленные модельные новые смысли y-факторов,

в которых модельные веса z-факторов отражают их относительные

силы воздействия на y-фактор (при 18 исходных индикаторах)

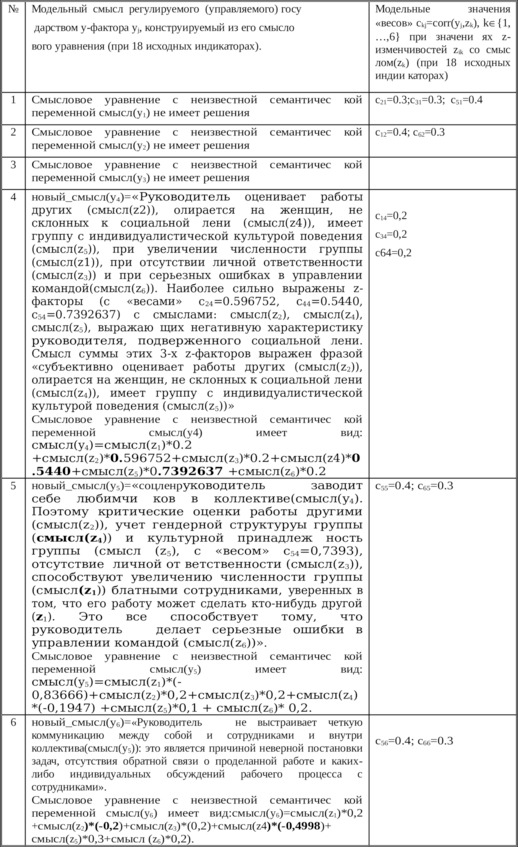
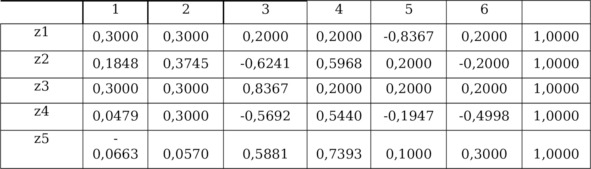
Таблица 5.4. Вид таблицы-программы Оптимизационной

задачи 2 с 18 исходными индикаторами

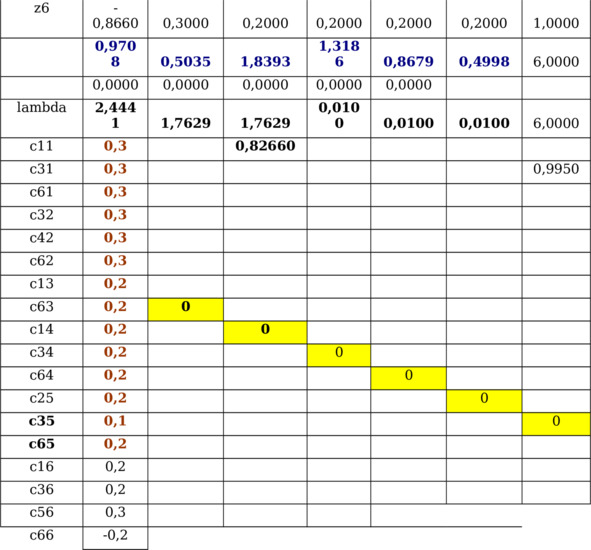
§5.6 Моделирование числоых матриц Y (t) m6. Z (t) m6

y- и z—отклонений для 3-х многосмысловых уравнений

по математической модели, где отдельно моделировались матрицы Um6 и Ym6 такие, что (1/m) UTm6Um6=I66,Ym6=Um6Λ1/2nn, затем моделирова лась матрица Zm6=Ym6Cт66. Матрицы Zm6 и Ym6 содержат модельные значения неизмеряемых изменчивостей (отклонений от 0), соответствующих неизмеряемым

Моделирование матрицы псевдособственных векторов С66 и псевдособственных чисел Λ66 проведено при решении Оптимиза ционной задачи 2: CCт=Inn, CтC¹Inn.

Результаты азработки 6 многосмысловых уравнений с известными и неизвестными семантическими переменными приведено в Таблице 5.3. Среди 6 вновь выявленных модельных смыслов 6 y-факторов, в которых модельные веса z-факторов отражают их относительные силы воздействия на один y-фактор (при 16 исходных индикаторах) найден только 1 смысл одного y-фактора y6.

Моделирование новых матриц Ym6,Zm6, соответствующих найденному выше многосмысловому уравнению проведено по математической модели, где отдельно моделировались матрицы Um6 и Ym6 такие, что (1/m) UTm6Um6=I66,Ym6=Um6Λ1/2nn, затем моделирова лась матрица Zm6=Ym6Cт66. Матрицы Zm6 и Ym6 содержат модельные значения неизмеряемых изменчивостей (отклонений от 0), соответствующих неизмеряемым значениям семантических (смысловых) переменных, характеризующих явление «ложное соавторство». Визуализация знаний о весах и z-, y- изменчивостях в случае их зависимости от «стимулирования активности научой работы в вузе» адекватно отражает познающую способность модели.

Только 6-ое смсловое уравнение смысл (y6) =смысл (z1) *0.4231Åсмысл (z2) * (-0.2435) Åсмысл (z3) *0.4000+смысл (z4) *0.1826Åсмысл (z5) *0.2300Åсмысл (z6) *0.2600 с семантическими переменными является имеющим практически смысл решением Когнитивной Моделью Ситуации с Ложным Соавторством. Найдем модельные значения y- и z—отклонений, являющихся числовыми переменными математической модели, соответствующей своему смысловому уравнению смысл (yi6) =смысл (zi1) *0.4231Åсмысл (zi2) * (-0.2435) Åсмысл (zi3) *0.4000Åсмысл (zi4) * 0.1826Åсмысл (zi5) *0.2300 Åсмысл (zi6) *0.2600 со своими семантическими 7 переменными смысл (zi1),…,смысл (zi6), смысл (yi6), i=1,…,m. Смысли z—отклонений заданы в исходных данных решаемой задачи, смысл y-отклонений смысл (yi6) мы конструировали выше. Математическая модель состоит из матриц Um6 и Ym6 таких, что (1/m) UTm6Um6=I66,Ym6=Um6Λ1/2nn, Zm6=Ym6Cт66. При этом верны равенства Λ66= (1/m) YTm6Ym6, C66= (1/m) ZTm6Ym6, где матрица C66 по построению (после решения решения Оптимизационной задачи 2) является матрицей псевдособственных векторов: CCт=Inn, CтC¹Inn. Матрица Y (t) m6, t=1,…,µ, обеспечивает случайность будущих значений y- и z—отклонений из матриц Y (t) m6. Z (t) m6. В матрице Ym6 элементы j—го столбца y1j,y2j,…,ymj (j-ая y-переменная, j=1,…,6) имеют среднее арифметическое, равное нулю: (1/m) (y1j+y2j+ …+ymj) =0, и дисперсию равную λj: (1/m) (y21j+y22j+ …+y2mj) =λj, при этом сумма дисперсий равна 6: λ1+…+λ6=6. Матрицы Ym6,Zm6=Ym6CT66,, приведены в Таблицах 5.7 и 5.8. Из 6 вновь выявленных модельных смысловых уравнений, образующих систему, практическую ценность имеет только смысловое уравнение вида смысл (yi6) =смысл (zi1) *0.4231Åсмысл (zi2) * (-0.2435) Å смысл (zi3) *0.4000Åсмысл (zi4) *0.1826Åсмысл (zi5) *0.2300Åсмысл (zi6) *0.2600. Остальные уравнения из системы проанализируем в отдельном исследовании. В нашем уравнении y-фактор y6 влияет на 6 модельные «веса» 0.4231, (-0.2435), 0.4000, 0.1826, 0.2300,0.2600. они отражают их относительные силы воздействия на y-фактор y6 (при 16 исходных индикаторах).

Для семантической переменной смысл (y6) с исходным смыслом смысл (y6) =«стимулирование активности научой работы (в т. ч. „публикации в Скопусе“) студентов, магистрантов» нами получено смысловое уравнение с модельными параметрами. Они и смысли изменчивостей дали, как показано выше, уравнение с известными смыслами и слчайными значениями zk проявлений смыслов смысл (zk), k=1,…,6, k-ых z-переменных zk. Уравнение состоит из слагаемых вида: zik*сkj, i=1,…,m; j=1,….,6, i – номер момента времени измерения, j – номер z-переменной.

Далее моделируются случайные матрицы значений y-изменчивостей Ym6. z-изменчивостей Zm6. соответствующих своим системам многосмысловым уравнениям с известными и неизвестными семантическими (смысловыми) переменными. При моделировании Ym6 моделируется (после преобразования матрицы V0m6= {v0ij} значений равномерно распределенных на интервале [-1;1] случайных чисел (Таблица 5.3) v0ij. i=1.….24; j=1.….6) случайная декоррели рованная выборка (Таблица 5.4) – матрица Um6: (1/m) UTm6Um6=I66. Ym6=U m6Λ1/266 (1/m) YTm6Ym6=Λ66. а матрица Zm6=Y m6CT66. где (Λ66. С66.) – пара ранее смоделированных при решении Оптимизационной Задачи 2: (I66.I66) => (L66.С66) с заданной мозаикой индикаторов. матриц. У пары матриц (I66.I66) разные смысли (смысл (I66) ¹ смысл (I66)). Существует бесконечное множество пар модельных матриц (Z (t) m6.Y (t) m6). t=1.….µ. Визуализация динамик кривых (z1.z2.z3. z4. z5.z6.y1). (z2. z5. y2) (z1.z2.z3.z4. z5. z6.y3) изложена ниже.

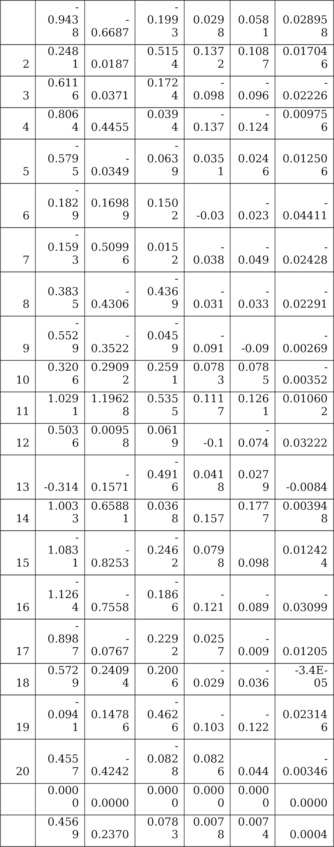
Таблица 5.5. Матрица С66= {cij=corr (zi. yj)} (z.y) -корреляций}

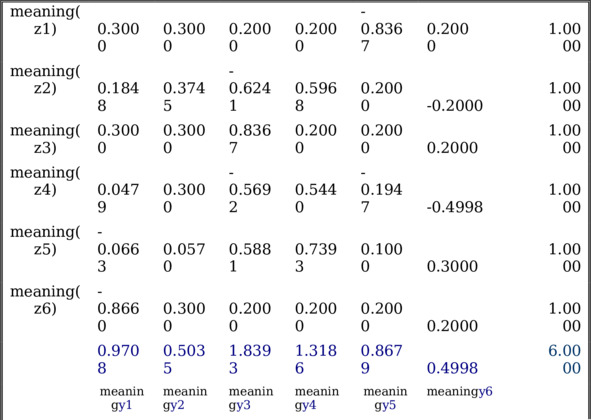
Таблица 5.6. Матрица V0m6 значений равномерно

распределенных в интервале [-1;1] случайных чисел

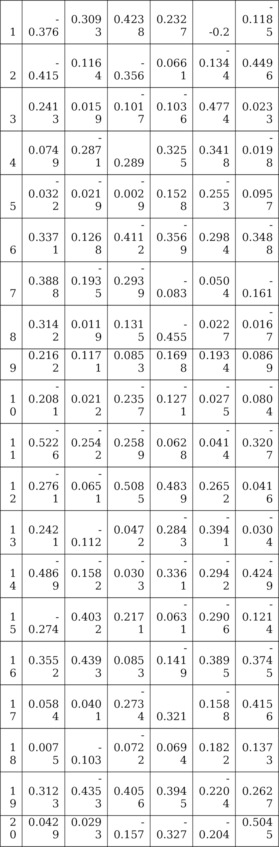
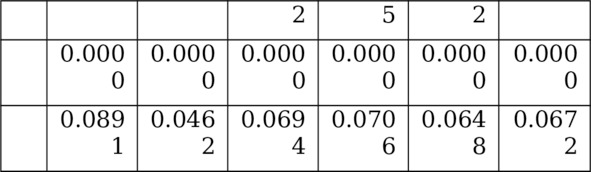
Таблица 5.7. Матрица Um6 u—изменчивостей

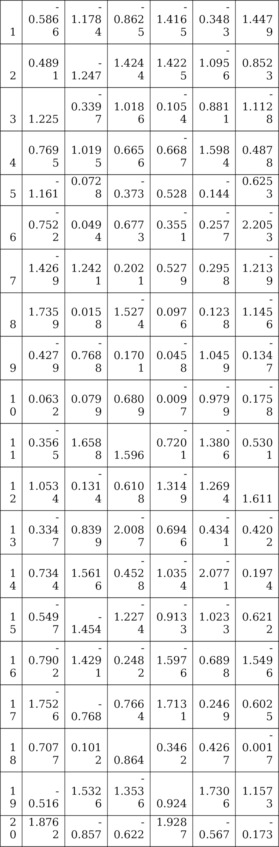
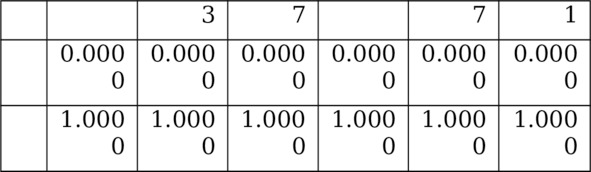
Таблица 5.8. Матрица Ym6 y—изменчивостей

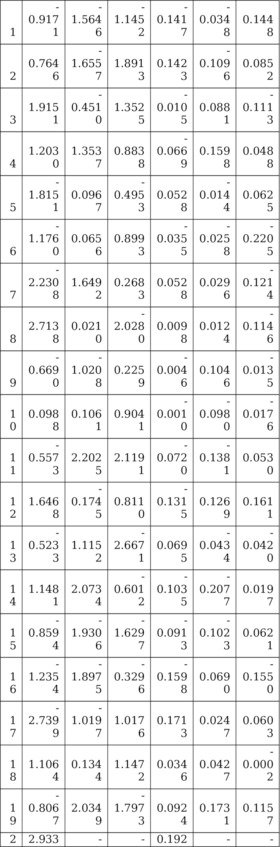
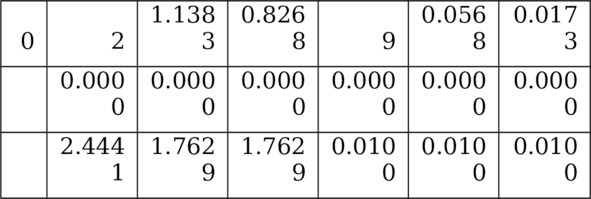
Таблица 5.9. Матрица Zm6 z—изменчивостей

§5.7 Визуализация знаний о «весах» и z-, y-изменчивостях

Точки на Рисунке 5.1 показывают взаимные динамики «скачки-падения» точек переменных (z2,z4,z5,y4). Эта визуализация позволяет узнать синхронноcть отклонений переменной z4 (смысл (z4) =«Гендерная принадлежность группы») при отклонении значения переменной z5 от 0 (смысл (z5) = «Культурная принадлежность группы»). График динамик пары z-отклонений (z4,z5) выделен отдельно (Рисунок 5.2). Мы обнаружили синхронность динамик этой пары отклонений от точки (0,0), теперь можно считать реальной познающую способность модели. На Рисунке 5.2 видим: во всех 20 точках наблюдается синхронность «скачков-падени» точек (zi4,zi5),i=1,…,20. Это означает «Гендерная (смысл (z4))» и «Культурная принадлежности группы (смысл (z5))» изменяются одинаково и оба фактора, из-за наличия заметных значений (сильной связи обеих переменных z4,z5 с переменной y4) с44=0,5440; с54=0,7393. Здесь мы видим работу модельных индикатора с44=0,5440; с54=0,7393, а не работу исходного значения индикаторов с14=0,2. Модель исправляет неправильно назначенные экспертом значения индикаторов. Свои замены значений индикаторов модель «обосновывает» как смысловыми (с семантическими переменными), так и алгебраическими (с числовыми переменными) равенствами. Обе переменные влияют на y —изменчивость фактора y4 соцлен-руководителя. Так выглядит краткий визуальный портрет соцлен-руководителя типа «соцлен-руководитель предоставляет дополнительные бонусы сотруднику зара нее».

Рассмотрим на Рисунке 5.3 тип соцлен-руководителя с новым_смыслом (y5) =«соцленруководитель заводит себе любимчиков в коллективе». Взаимная динамика 4-х z—изменчивостей z2, z3, z5, z6, влияющих на y —изменчивость фактора y5 со смыслом «соцлен-руководитель заводит себе любимчиков в коллективе…». Здесь на Рисунке 5.3 видим: критические оценки работы другими (смысл (z2)) сильно влияет (точки на кривой «z2» прыгают вверх-вниз) на «заводилу любимчиков в коллективе» (кривая «y5»). Немного слабее воздействует на кривую «y5» кривая «z3», еще слабее влияют кривые «z5», «z6». У данного типа соцленруководителя присутствует отрицательное отношение к учету гендерной структуруы группы (смысл (z4) с «весом» с46= (-0.4998)) и положительное отношение к культурной принадлежность группы (смысл (z5), с «весом» с54=0.3000), малая степень личной ответственности (смысл (z3), с «весом» с36=0.2000), способствуют увеличению численности группы (смысл (z1, с «весом» с16=0.2000)) блатными сотрудниками (их относительно мало, ибо с66=0.2), уверенных в том, что их работу будет сделать кто-нибудь другой.

Это все способствует тому, что соцлен-руководитель делает серьезные ошибки в управлении командой (смысл (z6))». Визуальная иллюстрация смыслового уравнения с неизвестной семантичес кой переменной смысл (y5) отражает его вид: смысл (y5) =смысл (z1) * (-0,83666) +смысл (z2) *0,2+ смысл (z3) * 0,2+смысл (z4) * (-0,1947) +смысл (z5) *0,1+смысл (z6) *0,2. Ттаков визуальный портрет соцлен-руководителя типа «Соцлен-руководитель предоставляет дополнительные бо нусы сотруднику зара нее».

Интересен визуальный портрет соцлен-руководителя типа Соцленруководитель пос тоянно идет навстречу тем, кто часто отпрашивается, просит какие-либо послабления в режиме работы и т.п.». Точки на Рисунке 5.4 показывают взаимные динамики «скачки-падения» точек переменных (z1,z2,z3,z4,z5, z6,y6).Смысловая формула новый_ смысл (y6) =смысл (z1) *0,2смысл (z2) * (-0.2) смысл (z3) * (0.2) смысл (z4) * (-0.4998) смысл (z5) *0.3+смысл (z6) *0.2) и соответствующая ей числовая формула y6=z1*0.2+ z2* (-0.2000) +z3* (0.2) +z4* (-0.4998) +z5*0.3+z6*0.2 имеют общий элемент l6=0.0100 из модельного спектра Λ66. Этот элемент показывает постоянную стабильность изменчивости переменной y6 по сравнению с изменчивостью 1-ой y-переменной y1:2.0000=disp (y1)> disp (y6) =0.0100.

В приложениях ОМ АГК (4—8) обычно ℓ <6 доминирующих элементов спектра Λ66 превосходят по величине 1, в то же время все дисперсии z-переменных равны 1. В нашей модели впервые встретился случай «дисперсии z-переменных (z1,z2,z3,z4,z5,z6,y6) больше, чем 1» Примечателен тот факт, что для 3-х самых слабо вариабельных (l4=l5=l6=0.0100) по степени отклонений от точки 0 y-факторов (y4,y5,y6) нам удалось (смотрите выше) сконструировать 3 семантических реений соответствующих смысловых уравнений. Остальные 3 смысловые уравнения не имеют когнитивного решения для своей самантической переменной. Этот интересный факт будет исследован в следующих статьях автора.

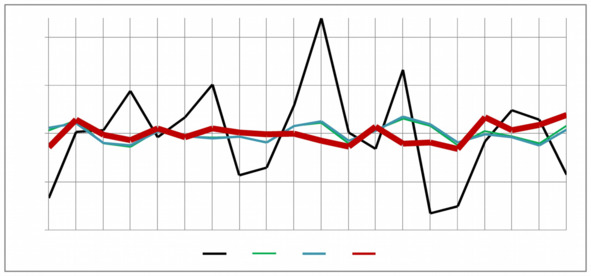
Рисунок 5.1. Взаимная динамика 3-х z -изменчивостей z2, z4, z5, влияющих на изменчивость на y —изменчивость фактора y4 со смыслом «соцлен-руководитель оценивает работы других, олирается на женщин, не склонных к социальной

лени, имеет группу с индивидуалистической культурой поведения»

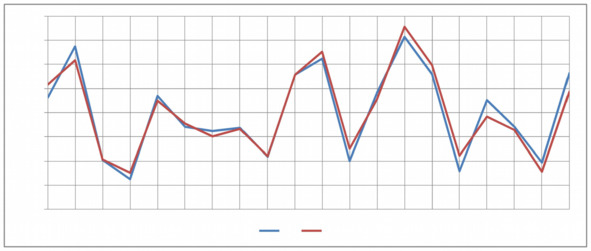
Рисунок 5.2. Тесная связь отражена в взаимной динамике 2-х z —изменчивостей z4, z5:

«Гендерная (смысл (z4))» и «Культурная принадлежность группы (смысл (z5))»,

влияющих на y —изменчивость фактора y4 соцлен-руководителя

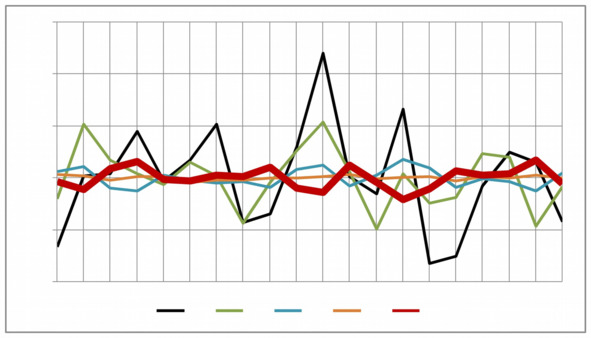
Рисунок 5.3. Взаимная динамика 4-х z – изменчивостей z2, z3, z5, z6, влияющих

на y —изменчивость фактора y5 со смыслом

«соцлен-руководитель заводит себе любимчиков в коллективе…»

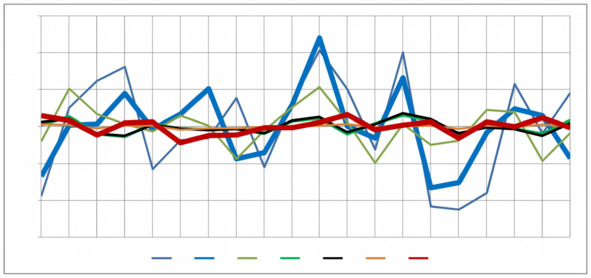
Рисунок 5.4. Взаимная динамика 6 z – изменчивостей, влияющих на

y —изменчивость фактора y6 со смыслом «соцлен-руководитель не выстраивает четкую коммуникацию между собой и сотрудниками и внутри коллектива…»

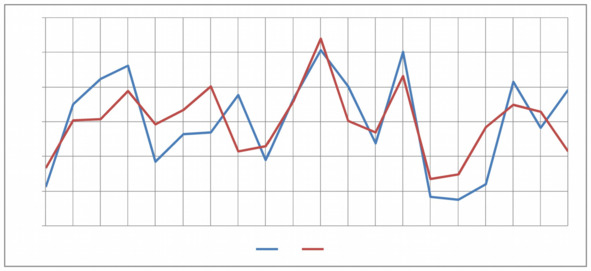
Рисунок 5.5. Тесная связь отражена в взаимной динамике 2-х z —изменчивостей z1, z2:

«увеличение численности группы (смысл (z1))» и «отсутствие оценки рабо ты другими (смысл (z2)», влияющих на y —изменчивость фактора y6 соцлен-руководителя

Рисунок 5.6. Обратные связи между z —изменчивостью z2, z4

И y —изменчивостью фактора y6 со смыслом «соцлен-руководитель

не выстраивает четкую коммуникацию между собой

и сотрудниками и внутри коллектива…»,

Рисунок 5.7. Заметная связь между z —изменчивостью z4 и y —изменчивостью

фактора y6 (с силой с246=0,49982) со смыслом «соцлен-руководитель не выстраивает четкую коммуникацию между собой и сотрудниками и внутри коллектива…»,

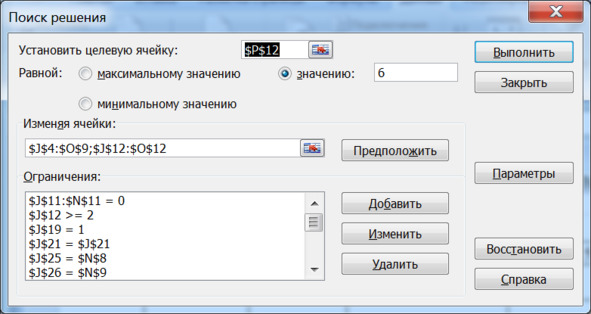
Рисунок 5.8. Окно надстройки «Поиск решения»

с операторами таблицы-программы решения

оптимизационной Задачи: (I66,I66) => (C66 Λ 66)

Заключение

Выше разработанная формализация явления «социальная лень» словесной модели Рингельмана, позволила соответствующей Когнитивной модели с смысловыми (с семантическими переменными) и многомерной математической модели (с числовыми переменными) реализовать, обосновать их формульное, фразеологическое, визуализированное на графиках описания поведений 2 субъектов модели: соцлен-руководитель и его сотрудники. Введены в модель (в соответствии эффектом Рингельмана) 12 семантических переменных: 6 – по смыслам независимые, 6 – взаимно зависимые. Введены математические параметры и z-, y-переменные: как некоррелированные (y-), так коррелированные (z-переменные). Для проверки алгеброй реального явления «социальная лень» сформулирована словесная модель, разработана Когнитивная Модель Явления «Социальная Лень». Модель обнаружила пропорции между долями информации, присущих переменным (y1,y2,y3,y4,y5,y6). Из 6 разработанных смсловых уравнений только 3 с 6 семантическими переменными являются имеющими практический смысл решениями Когнитивной Модели. Модель извлекла новые знания и адекватны реальным представлениям людй об соцлен-руководителе и его сотрудниках. Модель исправляет неправильно назначенные экспертом значения индикаторов. Свои замены значений индикаторов модель «обосновывает» как смысловыми (с семантическими переменными), так и алгебраическими (с числовыми переменными) равенствами. Вызуально видны на Рисунках 5.1—5.7 понятные взаимные динамики покаателей соцлен-руководителя и группы его сотрудников. Модель обнаружила пропорции между долями информации, присущих переменным (y1,y2,y3,y4,y5,y6). Из 6 разработанных смсловых уравнений только 3 с 6 семантическими переменными являются имеющими практически смысл решением Когнитивной Модели Явления «Социальная Лень». Для 3-х многосмысловых уравнений найденно числовое решение (пара случайных выборок Ym6,Zm6),Таблица 5.8 и 5.9) путем компьютерного моделирования матриц алгебраической системы уравнений. Они являются осмысленным решением, соответствующей системы уравнений с семантическими переменными. Смысл решения важнее, чем числовые значения решения. Получен новый факт: одинаковым величинам долей информации (0.010,0.010,0.010), присущих y-переменным (y4,y5,y6) соответствуют ущественно отличающиеся друг от друга новый_смысл (y4), новый_смысл (y5), новый_смысл (y6). Три смысловых уравнения дают более точный познающий эффект явлению «социальная лень» через формульное и фразеологическое описания поведения 2 субъектов (соцлен-руководитель и его подчиненные), описываемых в эффекте Рингельмана. Мы не не выходим за рамки, не исследуем факторы, порождающие само явление «социальная лень». Из описания эффекта следует, предпочтительность группы с индивидуалистической культурой поведения (смысл (z5), в Казахстане преобладает коллективистская культура поведения. Доцент Института психологии и образования КФУ, кандидат психологических наук Рамиль Гарифуллин: «Наше сознание является проективным и в этой проективности заключена его сущность. Иначе бы оно не состоялось, будучи раздавленным сложностью и нелинейностью мира. Компьютер, запрограммированный на основе математики, учитывающей нелинейность, способен преодолевать эту линейность. И самое главное нужно помнить, что обнаружение этой нелинейности произошло благодаря интеллекту самого человека! И не стоит разочаровываться в феномене Человека, даже если он имеет эгоистическую и потребительскую склонность к линейному и упрощенному восприятию Мира». Наша модель линейная, является первым шагом к нелинейной модели.

Глава 6. Когнитивная модель формулы жизни индивида

Введение

Комплекс тревожных переживаний о собственной жизни или о жизни близких людей, сообщения в СМИ о пожарах, наводнениях, изменениях климата, различные ограничения для существования индивидов из-за пандемии COVID 19 и т д заставляют нас менять уклад жизни. Люди боятся умереть, этот страх необходим для выживания во время пандемии COVID 19. Соблюдение вводимых правил работы, учебы, передвижения, общения заставляют нас иначе видеть вокруг происходящее, предельно точно воспринимать отклонения здоровья тела, души. Произошел «натурный» эксперимент над «живой» системой – изменились процессы, события, произошедшие в «живой» системе: в семье, на предприятиях, в районе, в области, в отрасли экономики, в республике.