Ātrā matemātika verbālās skaitīšanas noslēpumi

a) 21 x 26 = ___; b) 24 x 24 = ___; c) 23 x 23 = ___; d) 23 x 27 = ___; e) 21 x 36 = ___; e) 26 x 24 = ___

Jums vajadzētu būt iespējai atrisināt šos piemērus savā galvā. Tas nav grūti ar nelielu praksi.

Skaitļus, kas mazāki par 20, reizinot

Kā ir ar skaitļu reizināšanu, kas ir mazāki par 20? Ja tie (vai vismaz viens no tiem) ir lielāks par 15, bet mazāks par 20, kā atsauces numuru varat izmantot 20. Atrisināsim piemēru:

Izmantojot 20 kā atsauces numuru, mēs iegūstam:

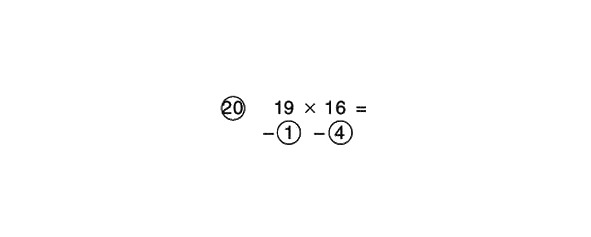
Atņemt šķērsām:

16 – 1 = 15 vai 19 – 4 = 15

Reiziniet ar 20:

15 x 2 = 30

30 x 10 = 300

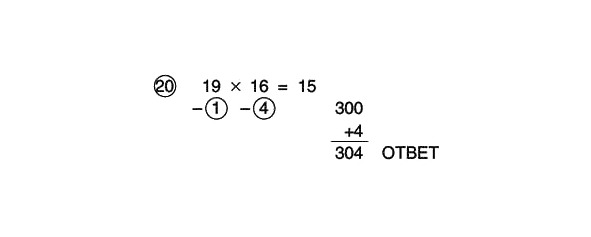
300 ir mūsu starpposma atbilde.

Tagad sareizināsim apļos esošos skaitļus un pievienosim rezultātu starpatbildei:

1 x 4 = 4

300 +4 = 304

Pilnībā atrisināts piemērs izskatās šādi:

Mēģināsim atrisināt to pašu piemēru, šoreiz izmantojot 10 kā atsauces numuru:

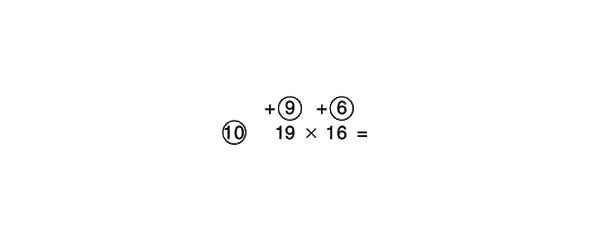
Saskaitīsim šķērsām un pēc tam reizinim rezultātu ar 10, iegūstot starpatbildi:

19 +6 = 25

10 x 25 = 250

Sareizināsim skaitļus apļos un rezultātu pievienosim starpatbildei:

9 x 6 = 54

250 +54 = 304

Pilnībā atrisinātais piemērs izskatās šādi:

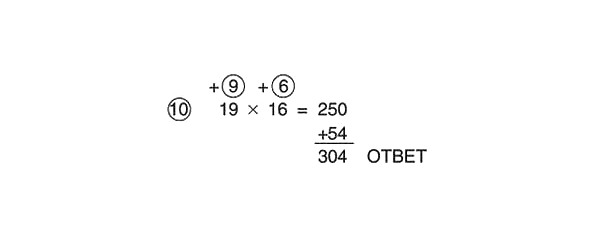
Tas apstiprina iepriekš iegūto rezultātu.

Nav lielas atšķirības starp diviem izmantotajiem atsauces numuriem. Tas ir personīgās izvēles jautājums. Vienkārši izvēlieties atsauces numuru, ar kuru jums ir vieglāk strādāt.

Skaitļi, kas ir lielāki un mazāki par 20

Trešais gadījums ir, kad viens skaitlis ir lielāks, bet otrs ir mazāks par 20. Piemēram:

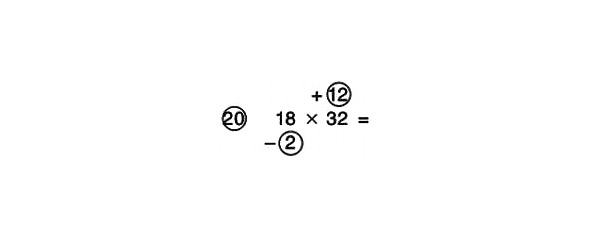
Varat pievienot 18 un 12 vai atņemt 2 no 32 un pēc tam rezultātu reizināt ar atsauces skaitli:

32 – 2 = 30

30 x 20 = 600

Tagad mēs reizinām skaitļus apļos:

2 x 12 = 24

Mēs faktiski reizinām mīnus 2 un 12, tāpēc atbilde ir -24.

600–24 = 576

Risinājuma piemērs izskatās šādi:

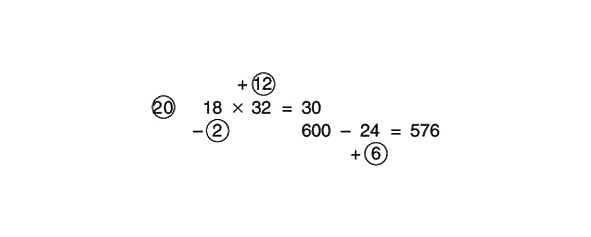
(Lai atņemtu 24, vispirms atņemiet 30 un pēc tam pievienojiet 6.)

Pārbaudīsim atbildi, izmetot devītniekus:

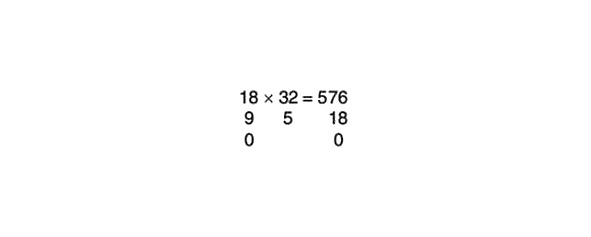
Produkts 0 x 5 ir 0, tātad atbilde ir pareiza.

Reizinot vēl lielākus skaitļus

Iepriekšējā sadaļā mēs runājām par skaitļu pāru reizināšanas metodi līdz 30 x 30. Ko darīt, ja jums ir jāreizina vēl lielāka izmēra skaitļi? Šajā gadījumā kā atsauces skaitli varat izmantot 50. Reizināt ar to ir vienkārši, jo 50 ir puse no 100 vai 100 dalīts ar 2. Tātad, lai reizinātu ar 50, vispirms var reizināt skaitli ar 100 un pēc tam dalīt rezultātu. ar 2.

Izmēģināsim to ar piemēru:

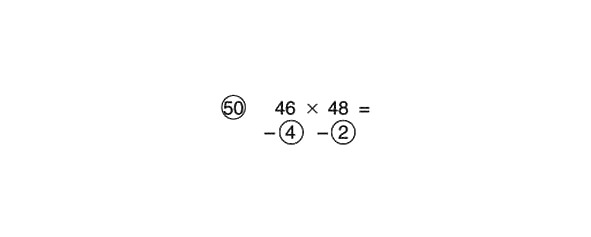
Atņemt šķērsām:

46 – 2 = 44 vai 48 – 4 = 44

Reiziniet 44 ar 100:

44 x 100 = 4400

Mēs sakām sev šādi: «44 uz 100 ir vienāds ar 4400.» Tagad mēs ņemam pusi, kas ir līdzvērtīga 44 reizināšanai ar 50, un mēs iegūstam 2200.

4400: 2 = 2200

Tagad sareizināsim skaitļus apļos un saskaitīsim rezultātu ar 2200:

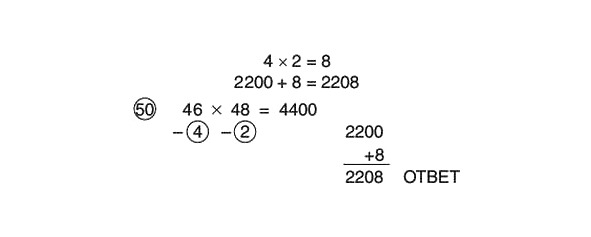
Kas var būt vienkāršāks? Apskatīsim citu piemēru:

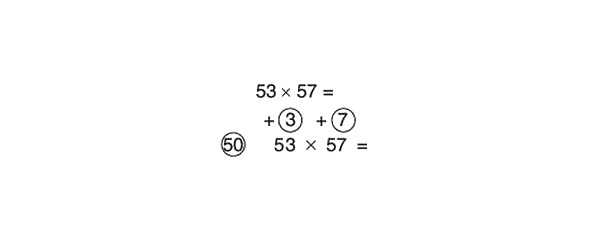
Mēs saskaitām šķērsām, pēc tam reiziniet rezultātu ar atsauces skaitli (reiziniet ar 100 un pēc tam dalām ar 2):

57 +3 = 60

60 x 100 = 6000

6000: 2 = 3000

Reiziniet skaitļus apļos un pievienojiet rezultātu 3000:

3 x 7 = 21

3000 +21 = 3021

Pilnībā atrisinātais piemērs tagad izskatās šādi:

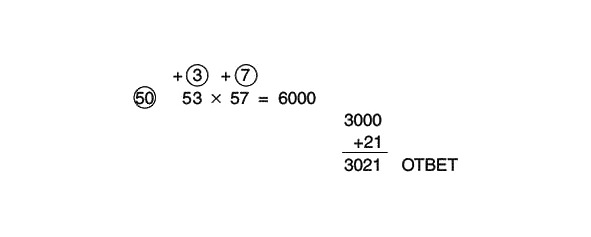
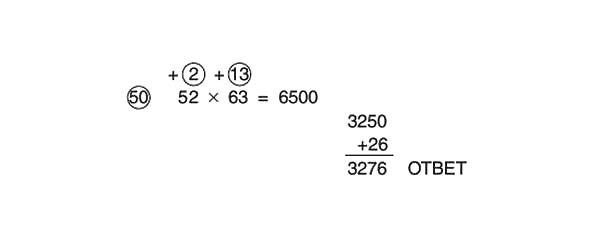
Atrisināsim šādu piemēru:

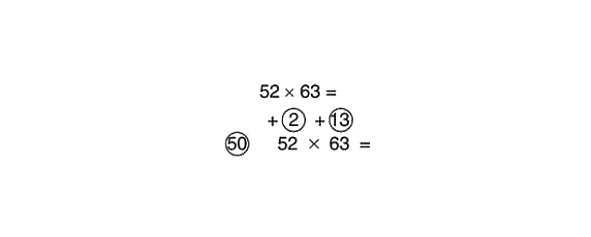
Mēs saskaitām šķērsām un reizinim rezultātu ar atsauces skaitli (vispirms reiziniet ar 100 un pēc tam daliet rezultātu ar 2):

63 +2 = 65

65 x 100 = 6500

Tagad mums ir jādala ar 2.

Nekādu problēmu! Mēs sakām sev: «Puse no sešiem tūkstošiem ir trīs tūkstoši. Puse no piecsimt ir divi simti piecdesmit. Kopā ir trīs tūkstoši divi simti piecdesmit.

Tagad reizināsim skaitļus apļos:

2 x 13 = 26

Pievienojot 26 starprezultātam 3250, mēs iegūstam 3276. Pilnībā atrisinātais piemērs tagad izskatās šādi:

Pārbaudīsim atbildes pareizību, izmetot devītniekus:

6 plus 3 koeficientā 63 ir vienāds ar 9, kas ir izsvītrots, atstājot aiz 0.

Atbilde ir 3 +6 = 9 un 2 +7 = 9, tas ir, visi skaitļi ir izsvītroti. 7 reizes 0 ir vienāds ar 0, tāpēc atbilde ir pareiza.

Es piedāvāju vairākus piemērus jūsu risinājumam. Centieties savā galvā atrisināt pēc iespējas vairāk piemēru.

a) 46 x 42 = ___; b) 47 x 49 = ___; c) 46 x 47 = ___; d) 44 x 44 = ___; e) 51 x 55 = ___; e) 54 x 56 = ___; g) 51 x 68 = ___; h) 51 x 72 = ___

Atbildes:

a) 1932. gads; b) 2303; c) 2162; d) 1936. gads; e) 2805; f) 3024; g) 3468; h) 3672

Kā jūs tikāt galā ar uzdevumu? Ja iepriekš esi pietiekami trenējies, tev nevajadzētu rasties problēmām to risināšanā savā galvā. Pārbaudiet savas atbildes, izvelkot deviņus.

Divkāršošana un samazināšana uz pusi

Lai kā atsauces skaitļus izmantotu 20 un 50, jums ir jāspēj viegli dubultot un samazināt skaitļus uz pusi.

Reizēm, kad, piemēram, mums ir jādala uz pusēm divciparu skaitlis, kura desmitnieku skaitlis ir nepāra, atbilde pati par sevi neliecina. Piemēram:

78: 2 =

Lai uz pusi samazinātu 78, varat dalīt 70 ar 2, pēc tam 8 un pēc tam pievienot rezultātus. Bet ir vēl vienkāršāks veids.

78 = 80—2. Puse no 80 – 2 ir vienāda ar 40 – 1. Šī ir atbilde:

40 – 1 = 39

Lai dubultotu 38, garīgi iedomājieties šo skaitli kā 40 – 2. Divkāršot vērtību, tā būs 80 – 4, tas ir, 76.

Mēģiniet pats atrisināt šādus piemērus:

a) 38 x 2 = ___; b) 29 x 2 = ___; c) 59 x 2 = ___; d) 68 x 2 = ___; e) 39 x 2 = ___; e) 47 x 2 =

Atbildes:

a) 76; b) 58; c) 118; d) 136; e) 78; e) 94

Tagad atrisiniet šos piemērus:

a) 38: 2 = ___; b) 56: 2 = ___; c) 78: 2 = ___; d) 94: 2 = ___; e) 34: 2 = ___; e) 58: 2 = ___; g) 18: 2 = ___; h) 76: 2 = ___

Atbildes:

a) 19; b) 28; c) 39; d) 47; e) 17; f) 29; g) 9 h) 38

To pašu pieeju var izmantot, lai reizinātu un dalītu diezgan lielus skaitļus ar 3 un 4. Piemēram:

19 x 3 = (20 – 1) x 3 = 60 – 3 = 57

38 x 4 = (40 – 2) x 4 = 160 – 8 = 152

Numuri 200 un 500 kā atsauces numuri

Ja reizinātie skaitļi ir tuvu 200 vai 500, aprēķini nav īpaši sarežģīti, jo gan 200, gan 500 ir viegli izmantot kā atsauces skaitļus.

Kā, piemēram, atrodam produktu 216 x 216? Ja kā atsauci izmantojat 200, piemēru var viegli atrisināt, tostarp jūsu galvā:

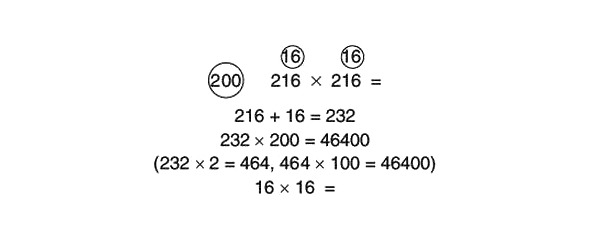
Mēs aprēķinām 16 x 16, izmantojot 10 kā atsauces skaitli.

Kā ar 512x512?

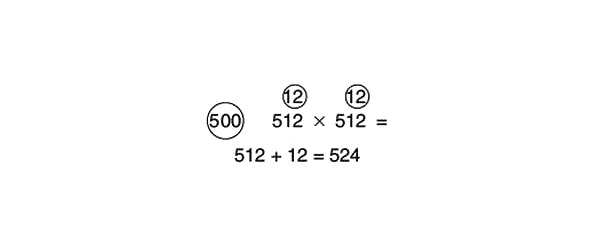
512 x 500 ir vienāds ar 524 x 1000 dalīts ar 2.

524 x 1000 = 524 000 jeb 524 tūkst.

Puse no 524 tūkstošiem ir vienāda ar 262 tūkstošiem.

Lai 524 tūkstošus sadalītu uz pusēm, tos var sadalīt uz 500 tūkstošiem un 24 tūkstošiem. Pusi no abiem skaitļiem ir viegli aprēķināt galvā. Puse no 500 tūkstošiem ir vienāda ar 250 tūkstošiem. Puse no 24 tūkstošiem ir vienāda ar 12 tūkstošiem. 250 tūkstoši plus 12 tūkstoši dod 262 tūkstošus.

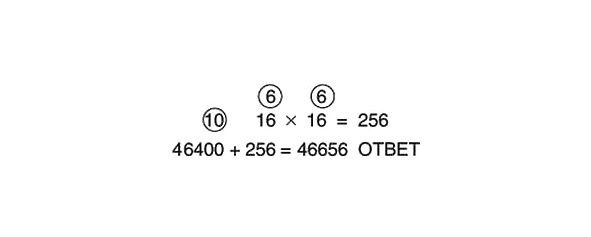
Tagad reizināsim skaitļus apļos:

12 x 12 = 144

262000 +144 = 262144 ATBILDE

Mazāku skaitļu reizināšana

Mēģināsim atrast produktu 6 x 4:

Kā atsauces skaitli izmantojam 10. Zem faktoriem ievelkam apļus, jo gan 6, gan 4 ir mazāki par 10. Atņem šķērsām:

6–6 = 0 vai 4–4 = 0

Tagad reizināsim skaitļus apļos:

4 x 6 =

Mēs esam atgriezušies pie sākotnējās problēmas (6 x 4). Šķiet, ka metode mums nekādi nepalīdzēja. Vai ir iespējams panākt, lai tas darbotos arī šādos gadījumos? Tas ir iespējams, taču šim nolūkam ir jāizmanto cits atsauces numurs. Mēģināsim pieņemt skaitli 5 kā tādu. 5 ir 10 dalīts ar 2, vai puse no 10. Visvieglāk reizināt ar 5 var, reizinot ar 10 un rezultātu dalot ar 2.

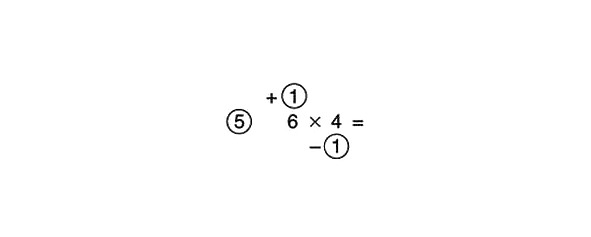
6 ir lielāks par 5, tāpēc mēs tam uzzīmējam apli. 4 ir mazāks par 5, tāpēc aplis tam tiek novilkts zemāk. 6 ir vairāk nekā 5 reizes 1, tāpat kā 4 ir mazāks par 5 reizi 1, tāpēc katrā aplī ierakstām 1.

Pievienojiet 4 un 1 šķērsām vai atņemiet 1 no 6:

6–1 = 5 vai 4 +1 = 5

Mēs reizinām 5 ar atsauces numuru, kas arī ir 5.

Lai to izdarītu, mēs vispirms reizinām ar 10, kas dod mums 50, un pēc tam rezultātu sadalām ar 2, iegūstot 25. Tagad mēs reizinām skaitļus apļos:

1 x -1 = -1

Tā kā rezultāts ir negatīvs skaitlis, mēs to atņemam no starpatbildes, nevis pievienojam tai:

25 – 1 = 24

Tādējādi:

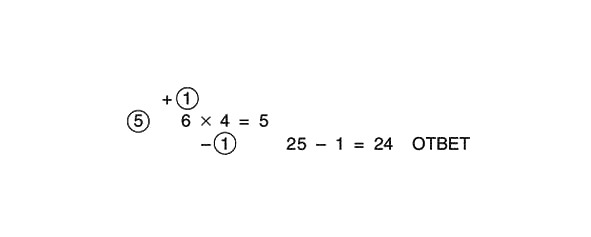
Tas ir ļoti garš un apgrūtinošs nelielu skaitļu reizināšanas veids, taču tas parāda, ka ar nelielu atjautību metodi var panākt, lai tā darbotos visos gadījumos. Turklāt šādas pieejas palīdz attīstīt sānu domāšanas spēju, kas ir ļoti svarīga matemātiķim un vispār jebkuram cilvēkam, ja viņš vēlas gūt panākumus dzīvē.

Apskatīsim vēl vienu piemēru, pat ja jūs labi zināt reizināšanas tabulu:

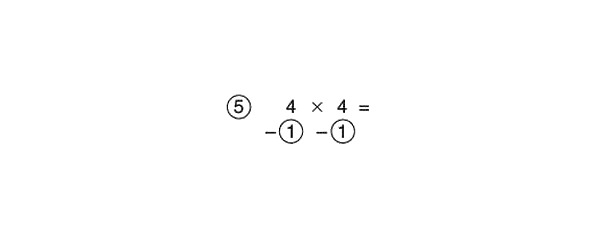
Atņemt šķērsām:

4—1 = 3

Sareizināsim rezultātu ar atsauces numuru:

3 x 10 = 30

30: 2 = 15

Tagad reizināsim skaitļus apļos:

1 x 1 = 1

Pievienosim šo rezultātu starpatbildei:

15 +1 = 16

Tādējādi:

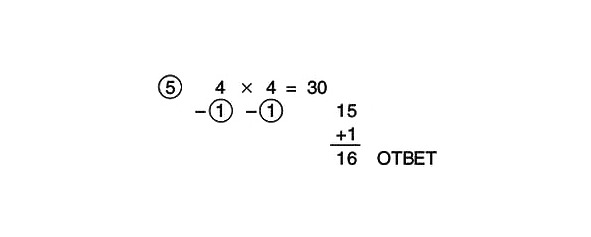
Mēģiniet pats atrisināt šādus piemērus:

a) 3 x 4 = __; b) 3 x 3 = __; c) 6 x 6 = __; d) 3 x 6 = __; e) 3 x 7 = __; e) 4 x 7 = __

Atbildes:

a) 12; b) 9; c) 36; d) 18; e) 21; e) 28

Esmu pārliecināts, ka šo piemēru risināšana jums nesagādāja ne mazāko problēmu. Es nedomāju, ka tas ir labākais veids, kā apgūt reizināšanas tabulas maziem skaitļiem. Manuprāt, visvieglāk ir to iemācīties. Bet daži cilvēki vēlas uzzināt, kā reizināt mazus skaitļus, izmantojot šo metodi, lai pārbaudītu tās daudzpusību. Citiem tas var patikt, jo viņi būs pārliecināti, ka pat tad, ja viņi aizmirst savas laika tabulas, ir vienkāršs veids, kā aprēķināt nepieciešamo produktu. Turklāt, pat ja jūs zināt savas reizināšanas tabulas no galvas, dažreiz var būt noderīgi un jautri spēlēt šādas spēles un eksperimentēt ar skaitļiem.

Reiziniet ar 5

Kā redzējām, lai reizinātu ar 5, vispirms var reizināt ar 10 un pēc tam rezultātu dalīt uz pusi. 5 ir vienāds ar pusi no 10. Lai reizinātu 6 ar 5, varat reizināt 6 ar 10, kas dod 60, un pēc tam rezultātu dalīt uz pusēm, iegūstot 30.

Izmēģiniet to pats:

a) 8 x 5 = __; b) 4 x 5 = __; c) 2 x 5 = __; d) 6 x 5 = __

Atbildes:

a) 40; b) 20; pulksten 10; d) 30

Bet ko darīt, ja desmitnieku skaits ir nepāra. Reiziniet 7 ar 5:

7 x 10 = 70

Ja jums ir grūti uzreiz sadalīt 70 uz pusēm, iedomājieties to kā summu: 60 +10. Tās puse ir 30 +5, kas ir 35.

Apskatīsim citu piemēru:

9 x 5 =

9 reiz 10 ir vienāds ar 90. 90 var uzrakstīt kā 80 +10. Puse no 80 +10 ir 40 +5, tātad atbilde ir 45. Atrisiniet paši:

a) 3 x 5 = __; b) 5 x 5 = __; c) 9 x 5 = __; d) 7 x 5 = __;

Atbildes:

a) 15; b) 25; c) 45; d) 35

Šis ir vienkāršs veids, kā uzzināt skaitļa 5 laika tabulas. Tas darbojas, ja skaitļi tiek reizināti ar 5. Piemēram:

14 x 5 =

14 x 10 = 140, un 140 dalīts ar 2, iegūst 70.

Tāpat:

23 x 5 =

23 x 10 = 230

230 = 220 +10

Puse no 220 +10 ir 110 +5

110 +5 = 115

Visus šos aprēķinus pēc nelielas prakses var izdarīt daudz ātrāk savā galvā.

6. nodaļa Decimālskaitļu reizinājums

Cipari sastāv no cipariem: 0, 1, 2, 3, 4, 5, 6, 7, 8 un 9. Cipari ir kā burti, kurus mēs izmantojam vārdu veidošanai. 23 ir divciparu skaitlis, kas sastāv no cipariem 2 un 3. Cipara atrašanās vieta ciparā nosaka šim ciparam atbilstošo ciparu. Piemēram, skaitlis 2 ciparā 23 atbilst desmitvietai un nozīmē 2 desmitniekus, bet cipars 3 atbilst vienību vietai un nozīmē 3 vienības. 435 ir trīsciparu skaitlis. Skaitlis 4 atbilst simtu vietai un apzīmē 4 simtus jeb 400. Skaitlis 3 atbilst desmitnieku skaitam un apzīmē 3 desmitniekus jeb 30. Skaitlis 5 atbilst vienību skaitam un apzīmē 5 vienības vai vienkārši 5. Kad mēs rakstām skaitli, secībai, kādā uz tā atrodas cipari, nav maza nozīme.

Kad mēs rakstām cenu vai skaitli, kas apzīmē naudas daudzumu, mēs izmantojam komatu, lai atdalītu dolārus no centiem. Piemēram, 1,25 ASV dolāri nozīmē 1 dolāru un 25 dolāra simtdaļas (25 centus). Pirmais cipars aiz komata apzīmē dolāra desmitdaļas (10 10 centu monētas ir vienādas ar 1 USD). Otrais cipars aiz komata apzīmē dolāra simtdaļas (100 centi ir vienāds ar 1 USD).

Decimāldaļu reizināšana [2] nav sarežģītāka darbība par jebkuru citu skaitļu reizināšanu. Apskatīsim piemērus.

Piemēram:

1,3 x 1,4 =

(1,3 – viens punkts un trīs desmitdaļas; 1,4 – viens punkts un četras desmitdaļas.)

Mēs rakstām piemēru tādu, kāds tas ir, bet nepievērš uzmanību komatiem:

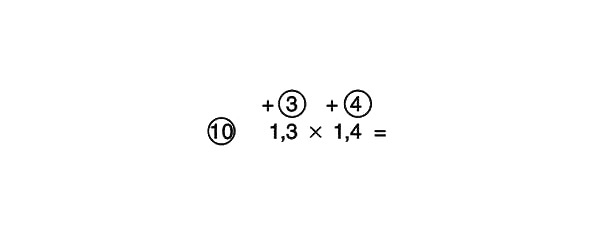
Lai gan mēs rakstījām 1,3 x 1,4, mēs atrisināsim piemēru tā, it kā tas izskatītos šādi:

13 x 14 =

Aizmirstiet par komatu un sakiet sev: «Trīspadsmit plus četri ir septiņpadsmit, reizināts ar desmit, simts septiņdesmit. Četras reiz trīs ir divpadsmit. plus simts septiņdesmit. simts astoņdesmit divi».

Risinājuma piemērs izskatās šādi:

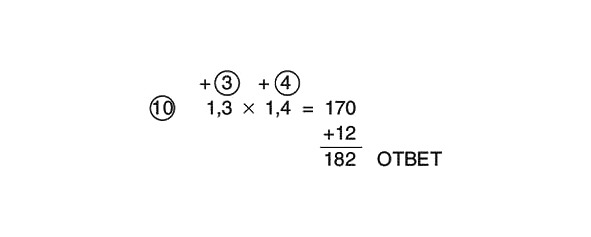
Taču mūsu vēlamais produkts bija 1,3 x 1,4, un līdz šim esam aprēķinājuši tikai 13 x 14. Piemērs nav pilnībā atrisināts. Mums ir jāizdomā, kur iegūtajā atbildē ievietot komatu. Lai to izdarītu, apskatīsim faktorus un saskaitīsim ciparu skaitu aiz komata. Aiz komata ir divi cipari: 3 1.3 un 4 1.4. Tā kā mums faktoros kopā ir divi cipari aiz komata, arī atbildē ir jābūt diviem cipariem aiz komata. Saskaitiet divus skaitļus no beigām un ievietojiet komatu starp skaitļiem 1 un 8.

1.82 ATBILDE

Vienkāršs veids, kā pārbaudīt iegūto atbildi, ir novērtēt to ar tuvinājumu. Tas nozīmē, ka tā vietā, lai izmantotu sākotnējos skaitļus (1,3 un 1,4), mēs tos noapaļosim attiecīgi līdz 1 un 1,5. reizinājums 1 x 1,5 dod 1,5. Tātad atbildei, ko mēs meklējam, ir jābūt kaut kur starp 1 un 2, nevis, piemēram, 20 vai 200. Tas ļauj mums zināt, ka esam izvēlējušies pareizo decimāldaļu.

Mēģināsim atrisināt šo piemēru:

9,6 x 97 =

Uzrakstīsim problēmu tā, kā tā ir norādīta, bet pieņemsim, ka runa ir par skaitļiem 96 un 97.

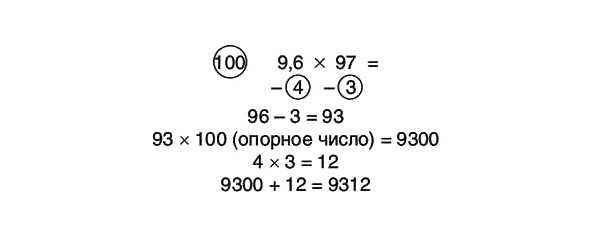
Kur likt komatu? Cik zīmju aiz komata ir piemēru faktoros? Viens. Atbildē ir jābūt tādam pašam ciparu skaitam pēc komata.

931.2 ATBILDE

Lai noteiktu, kur likt decimālzīmi, mums ir jāsaskaita kopējais ciparu skaits aiz komata abiem skaitļiem, kurus mēs reizinām. Neaizmirstiet pārliecināties, ka atbildē ir norādīts vienāds ciparzīmju skaits aiz komata. Mēs varam pārbaudīt atbildi, reizinot 10 (noapaļotā vērtība 9,6) ar 90 (noapaļotā vērtība 97), kas dod 900. Tagad mēs zinām, ka atbildei ir jābūt kaut kur ap skaitli 900. nevis 9000 vai 90..

Ja mēs reizinātu ar 9,6 un 9,7, atbilde būtu 93,12. Šis fakts var palīdzēt mums atrast veidus, kā vēl vairāk vienkāršot aprēķinus, kas citādi nebūtu tik acīmredzami. Drīzumā aplūkosim šīs iespējas. Tagad mēģiniet pats atrisināt šādus piemērus:

a) 1,3 x 1,3 = __; b) 1,4 x 1,4 = __; c) 14 x 0,14 = __; d) 96 x 0,97 = __; e) 0,96 x 9,6 = __; e) 13 x 1,5 = __

Atbildes:

a) 1,69; b) 1,96; c) 1,96; d) 93,12; e) 9,216; e) 19.5

Pieņemsim, ka jums bija jāatrisina šāds piemērs:

0,13 x 0,14 =

Atcerēsimies to:

13 x 14 = 182

Kur jāliek komats? Cik zīmju aiz komata ir abiem faktoriem? Četri: skaitļi 1 un 3 pirmajā faktorā un skaitļi 1 un 4 otrajā. Tāpēc atbildē ir jāskaita četri cipari, sākot no beigām. Mums būs jāpievieno viens cipars, jo mums ir trīsciparu atbilde (182). Tāpēc mēs saskaitām trīs ciparus un pievienojam 0.

Mūsu atbilde tagad izskatās šādi:

0,0182 ATBILDE

Pirms komata ir jāievieto arī 0, jo pirms tā vienmēr ir jābūt vismaz vienam ciparam. Mūsu gadījumā mēs pievienojam 0 kā ceturto ciparu pēc komata un arī ievietojam 0 pirms komata.

Apskatīsim vēl vienu piemēru, lai nostiprinātu to, ko esam iemācījušies:

0,014 x 1,4 =

14 x 14 = 196

Kur jābūt komatam? Reizinātājiem kopumā ir četri cipari aiz komata, proti: 0, 1 un 4 pirmajam reizinātājam un 4 otrajam. Tāpēc atbildē ir jābūt četriem cipariem aiz komata. Tā kā atbildē ir tikai trīs cipari, mēs pievienojam 0 kā ceturto zīmi aiz komata.

Atbilde ir:

0,0196 ATBILDE

Atrisiniet šādus piemērus pats:

a) 23 x 2,4 = __; b) 0,48 x 4,8 = __; c) 0,048 x 0,48 = __; d) 0,0023 x 0,23 = __

Viegli, vai ne?

Šeit ir atbildes uz kontroli:

a) 55.2; b) 2,304; c) 0,02304; d) 0,000529

Zinot šo vienkāršo principu, mēs varēsim atrisināt dažas problēmas, kas var šķist sarežģītas, ja tām pielietosim apgūto metodi. Pēc dažām problēmas nosacījumu izmaiņām risinājumu var ievērojami vienkāršot. Apskatīsim piemēru:

8 x 68 =

Kāds atsauces numurs ir jāizmanto šajā gadījumā? Varētu izmantot 10 kā atsauci koeficientam 8, bet 68 labāk izmantot 100, jo skaitļi ir tuvāk viens otram. Varbūt pamēģini 50? Tomēr mūsu metode darbojas labāk, ja skaitļi ir tuvu viens otram. Kā šajā gadījumā atrisināt problēmu? Kāpēc nerakstīt 8.0, nevis 8?

Nav atšķirības starp 8 un 8.0. Pirmais cipars (8) nozīmē, ka mums ir 8 vienības, bet otrais (8,0) nozīmē, ka mums ir 8 vienības līdz vienai zīmei aiz komata. Taču šī zīme, būdama nulle, neko ne pieskaita, ne neatņem no visas daļas (8).

Tātad mēs saņēmām:

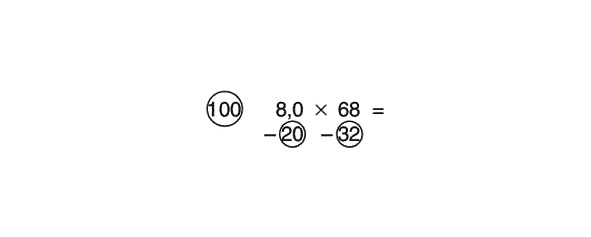
Tagad problēmu var viegli atrisināt. Atņemt šķērsām:

68–20 = 48

Mēs reizinām 48 ar atsauces numuru 100 un iegūstam 4800. Reiziniet skaitļus apļos.

20 x 32 = 640

(Lai reizinātu ar 20, vispirms reiziniet ar 2 un pēc tam ar 10, jo 2 x 10 = 20.)

4800 +640 = 5440

Tādējādi:

Tagad jums ir pareizi jāievieto decimālzīme. Cik ciparu aiz komata ir uzdevuma formulējuma faktoros? Viens, nulle, ko paši pievienojām. Tādējādi atbildē mēs saskaitām vienu ciparu no labās puses.

544.0 ATBILDE

Mēs parasti rakstām līdzīgu skaitli bez nulles aiz komata, tas ir, 544.

Mēģiniet pats atrisināt šādus piemērus:

a) 9 x 83 = __; b) 9 x 67 = __; c) 9 x 77 = __; d) 8 x 86 = __; e) 7 x 89 = __

Šeit ir atbildes uz kontroli:

a) 747; b) 603; c) 693; d) 688; e) 623

Piemēru risināšana nebija grūta, vai ne?

Ar nelielu iztēli jūs varat izmantot šīs pieejas, lai atrisinātu jebkuru reizināšanas problēmu.

7. nodaļa Reizināšana ar diviem atsauces skaitļiem

Mūsu reizināšanas metode lieliski darbojās skaitļiem, kuru lielums ļoti neatšķiras. Pretējā gadījumā metode arī darbojas, taču aprēķini būs apgrūtinošāki. Piemēram, ko darīt, ja mēs vēlētos aprēķināt, cik daudz ir 13 x 64? Kuru atsauces numuru mums vajadzētu izvēlēties? Šajā nodaļā apskatīsim vienkāršu metodi, kas ļauj ievērot vienu un to pašu stratēģiju, bet izmantojot divus atsauces numurus.

Varat reizināt divus skaitļus, kuru lielums ir ļoti atšķirīgs, izmantojot divus atsauces numurus. Vispirms iedziļināsimies lietas būtībā, un tad es jums parādīšu, kā šī metode darbojas. Kā piemēru ņemsim produktu 8 x 27. 8 ir tuvāk 10, tāpēc mēs izmantojam 10 kā pirmo atsauces numuru. 27 ir tuvāk 30, tāpēc

30 būs mūsu otrais atsauces numurs. No šiem skaitļiem izvēlieties to, ar kuru ir visvieglāk reizināt. Tā kā to ir ļoti viegli reizināt ar 10, mēs to izvēlēsimies. Tas būs mūsu galvenais atsauces numurs. Otrajam atsauces numuram ir jābūt galvenā numura reizinājumam. Mūsu izvēlētais skaitlis ir bāzes daudzkārtnis, kas ir trīs reizes lielāks par skaitli (30: 10 = 3). Tā vietā, lai zīmētu apli, es ierakstu divus atsauces numurus iekavās pa kreisi no piemēra nosacījuma.

Primārais atsauces numurs ir 10. Otrais atsauces numurs ir 30 jeb 3 x 10. Atsauces numurus rakstām iekavās kā otro skaitli, kas izteikts kā pirmais, tas ir: