Искусственный интеллект. Машинное обучение

Применение обучения без учителя позволяет извлечь ценные знания и понимание из данных, даже если мы не знаем правильных ответов заранее. Этот тип обучения находит широкое применение в различных областях, таких как анализ данных, исследования рынка, биоинформатика и многое другое.

Пример 1

Давайте рассмотрим пример задачи снижения размерности данных с использованием метода главных компонент (PCA) на наборе данных Breast Cancer Wisconsin (данные о раке груди).

```python

# Импортируем необходимые библиотеки

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.preprocessing import StandardScaler

from sklearn.decomposition import PCA

# Загрузим набор данных Breast Cancer Wisconsin

breast_cancer = load_breast_cancer()

X = breast_cancer.data

y = breast_cancer.target

target_names = breast_cancer.target_names

# Стандартизируем признаки

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

# Применим метод главных компонент (PCA) для снижения размерности до 2 компонент

pca = PCA(n_components=2)

X_pca = pca.fit_transform(X_scaled)

# Визуализируем результаты

plt.figure(figsize=(8, 6))

colors = ['navy', 'turquoise']

lw = 2

for color, i, target_name in zip(colors, [0, 1], target_names):

plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=.8, lw=lw,

label=target_name)

plt.legend(loc='best', shadow=False, scatterpoints=1)

plt.title('PCA of Breast Cancer Wisconsin dataset')

plt.xlabel('Principal Component 1')

plt.ylabel('Principal Component 2')

plt.show()

```

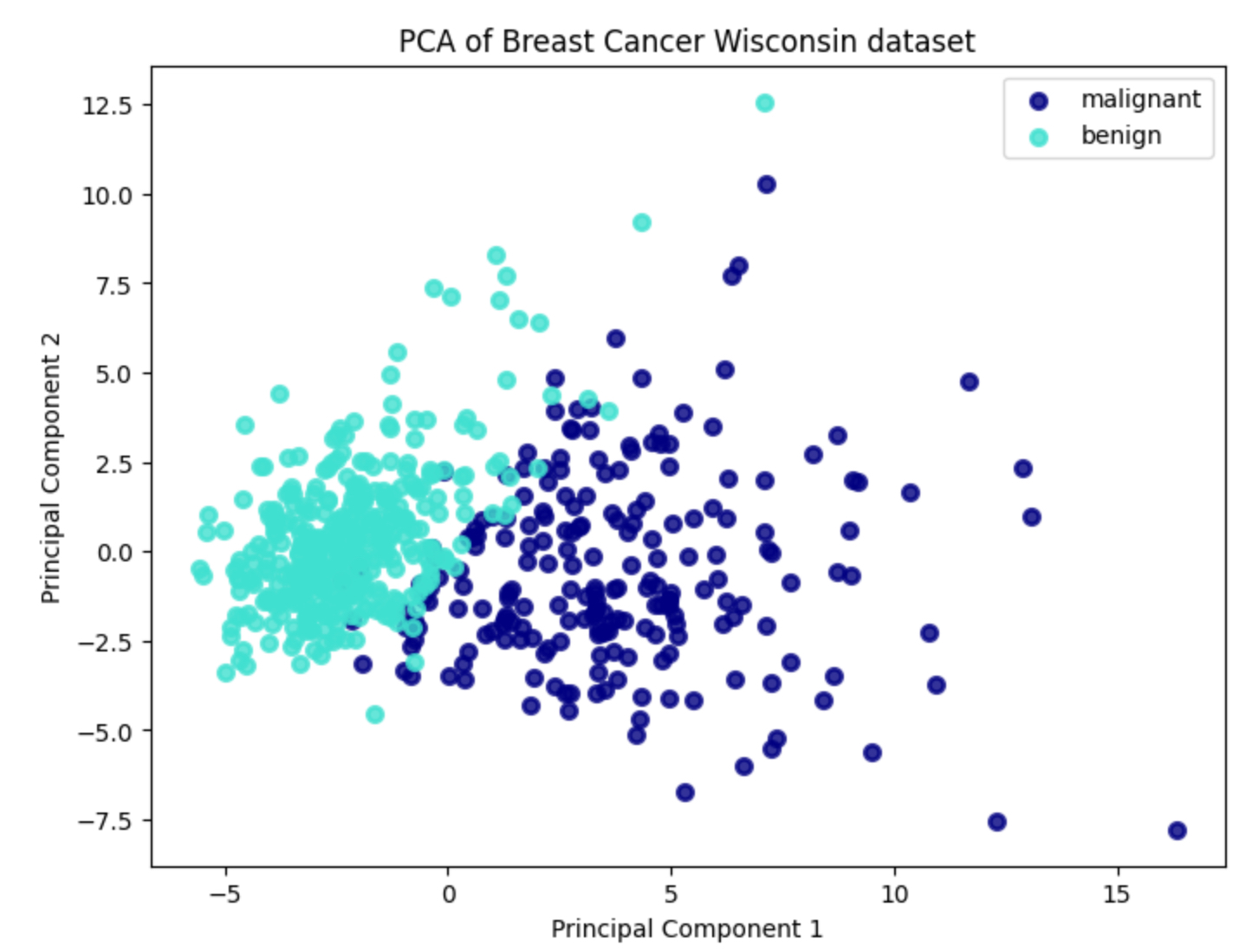
Этот код загружает набор данных Breast Cancer Wisconsin, стандартизирует признаки, применяет метод главных компонент (PCA) для снижения размерности до 2 компонент и визуализирует результаты. В результате получаем двумерное представление данных о раке груди, которое помогает нам лучше понять структуру и взаимосвязи между признаками.

Метод снижения размерности данных, такой как метод главных компонент (PCA), применяется здесь для уменьшения количества признаков (в данном случае, измерений) в наборе данных до двух главных компонент. Это делается с целью упрощения анализа данных и визуализации, при этом сохраняя как можно больше информации о вариативности данных.

В коде мы выполняем следующие шаги:

1. Загрузка данных: Мы загружаем набор данных о раке груди и разделяем его на признаки (X) и метки классов (y).

2. Стандартизация признаков: Перед применением PCA признаки стандартизируются, чтобы среднее значение каждого признака было равно 0, а стандартное отклонение равнялось 1. Это необходимо для обеспечения одинаковой значимости всех признаков.

3. Применение PCA: Мы создаем экземпляр PCA с параметром `n_components=2`, чтобы снизить размерность данных до двух главных компонент.

4. Преобразование данных: С помощью метода `fit_transform()` мы преобразуем стандартизированные признаки (X_scaled) в новое двумерное пространство главных компонент (X_pca).

5. Визуализация результатов: Мы визуализируем полученные двумерные данные, используя метки классов для раскрашивания точек на графике. Это позволяет нам увидеть, как объекты данных распределяются в новом пространстве главных компонент и какие зависимости между ними могут быть обнаружены.

Пример 2

Задача, рассмотренная в данном коде, заключается в кластеризации данных об опухолях молочной железы на основе их характеристик, чтобы выделить группы схожих образцов тканей. Это может помочь в анализе и понимании характеристик опухолей, а также в дальнейшем принятии медицинских решений.

Набор данных содержит информацию о различных признаках опухолей, таких как радиус, текстура, периметр и другие. Для удобства эти данные загружаются из библиотеки `sklearn.datasets`. Каждый образец в наборе данных имеет также метку класса, указывающую, является ли опухоль злокачественной (1) или доброкачественной (0).

Далее применяется метод кластеризации KMeans, который пытается разделить образцы данных на заданное количество кластеров (в данном случае 2 кластера). Модель KMeans обучается на признаках образцов без учета меток классов, так как это задача обучения без учителя. Подробнее данный метод мы будем рассматривать позже.

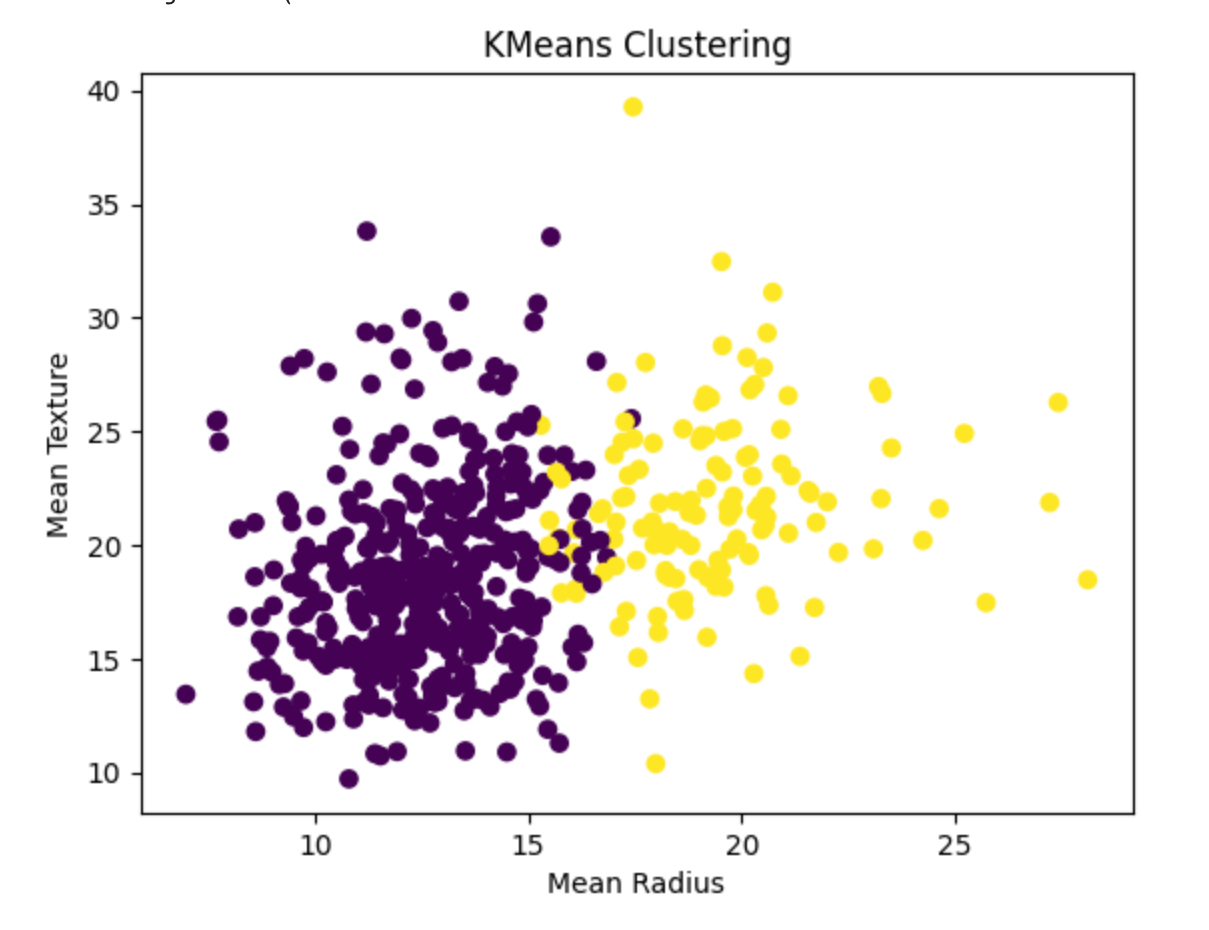
После обучения модели для каждого образца вычисляется метка кластера, которой он принадлежит. Затем происходит визуализация полученных кластеров на плоскости, используя два из признаков: средний радиус (`mean radius`) и среднюю текстуру (`mean texture`). Каждый образец представлен точкой на графике, а его цвет обозначает принадлежность к одному из двух кластеров.

Этот анализ помогает выявить общие характеристики опухолей и потенциально помогает в их классификации или определении риска злокачественного развития.

import pandas as pd

from sklearn.datasets import load_breast_cancer

from sklearn.cluster import KMeans

import matplotlib.pyplot as plt

# Загрузка набора данных

breast_cancer_data = load_breast_cancer()

# Преобразование данных в DataFrame

data = pd.DataFrame(data=breast_cancer_data.data, columns=breast_cancer_data.feature_names)

# Добавление меток классов в DataFrame

data['target'] = breast_cancer_data.target

# Создание объекта KMeans с 2 кластерами (для злокачественных и доброкачественных опухолей)

kmeans = KMeans(n_clusters=2)

# Обучение модели на данных без меток классов

kmeans.fit(data.drop('target', axis=1))

# Получение меток кластеров для каждого образца

cluster_labels = kmeans.labels_

# Визуализация кластеров

plt.scatter(data['mean radius'], data['mean texture'], c=cluster_labels, cmap='viridis')

plt.xlabel('Mean Radius')

plt.ylabel('Mean Texture')

plt.title('KMeans Clustering')

plt.show()

Пример 3

Давайте возьмем набор данных о покупках клиентов в магазине и применим к нему метод кластеризации K-means. В этом примере мы будем использовать набор данных "Mall Customer Segmentation Data", который содержит информацию о клиентах магазина и их покупках.

```python

# Импортируем необходимые библиотеки

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

from sklearn.preprocessing import StandardScaler

# Загружаем данные

data = pd.read_csv('mall_customers.csv')

# Посмотрим на структуру данных

print(data.head())

# Определяем признаки для кластеризации (в данном случае возраст и расходы)

X = data[['Age', 'Spending Score (1-100)']].values

# Стандартизируем данные

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

# Определяем количество кластеров

k = 5

# Применяем метод кластеризации K-means

kmeans = KMeans(n_clusters=k, random_state=42)

kmeans.fit(X_scaled)

y_pred = kmeans.predict(X_scaled)

# Визуализируем результаты кластеризации

plt.figure(figsize=(8, 6))

plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y_pred, cmap='viridis')

plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], marker='x', color='red', s=300, linewidth=5, label='Centroids')

plt.xlabel('Age')

plt.ylabel('Spending Score (1-100)')

plt.title('K-means clustering of Mall Customers')

plt.legend()

plt.show()

```

В этом коде мы загружаем данные о покупках клиентов, выбираем признаки для кластеризации (в данном случае возраст и расходы), стандартизируем данные, применяем метод кластеризации K-means и визуализируем результаты кластеризации. Каждый кластер обозначен разным цветом, а центроиды кластеров отмечены красными крестами.

В коде мы используем метод кластеризации K-means, который работает следующим образом:

1. Загрузка данных: Сначала мы загружаем данные о покупках клиентов из файла "mall_customers.csv".

2. Выбор признаков: Мы выбираем два признака для кластеризации – "Age" (возраст клиентов) и "Spending Score" (расходы клиентов).

3. Стандартизация данных: Поскольку признаки имеют разные диапазоны значений, мы стандартизируем их с помощью `StandardScaler`, чтобы все признаки имели среднее значение 0 и стандартное отклонение 1.

4. Определение количества кластеров: В данном примере мы выбираем 5 кластеров, но это число можно выбирать исходя из предпочтений или на основе бизнес-задачи.

5. Применение метода кластеризации K-means: Мы создаем объект `KMeans` с указанным количеством кластеров и применяем его к стандартизированным данным методом `fit`. Затем мы используем полученную модель для предсказания кластеров для каждого клиента.

6. Визуализация результатов: Мы визуализируем результаты кластеризации, размещая каждого клиента на плоскости с осью X (возраст) и осью Y (расходы), окрашивая их в соответствии с прогнозируемым кластером. Также мы отображаем центры кластеров (центроиды) красными крестами.

Обучение с подкреплением (Reinforcement Learning)

Обучение с подкреплением представляет собой класс задач машинного обучения, где модель, называемая агентом, взаимодействует с окружающей средой и принимает решения с целью максимизации некоторой численной награды или минимизации потерь. Этот процесс аналогичен обучению живых существ в реальном мире: агент получает обратную связь в виде вознаграждения или наказания за свои действия, что помогает ему корректировать свое поведение и принимать лучшие решения в будущем.

Основной целью обучения с подкреплением является нахождение стратегии действий, которая максимизирует общее суммарное вознаграждение в течение длительного периода времени. Для этого агент должен учитывать текущее состояние окружающей среды, возможные действия и ожидаемые награды или потери, чтобы выбирать наилучшие действия в каждый момент времени.

Примеры задач обучения с подкреплением включают обучение агентов в компьютерных играх, где агенту нужно изучить стратегии для достижения победы или достижения определенных целей, а также управление роботами в реальном мире, где агенту нужно принимать решения на основе восприятия окружающей среды и выполнения задач, например, перемещение в пространстве или выполнение определенных действий.

Пример 1

Давайте рассмотрим пример задачи обучения с подкреплением на простом примере – агент играет в игру "Сетка мира" (Gridworld). В этой игре агент находится на игровом поле, представленном в виде сетки, и его целью является достижение целевой ячейки, избегая при этом препятствий.

Для начала определим игровое поле. Давайте создадим сетку размером 4x4, где каждая ячейка может быть либо пустой, либо содержать препятствие или целевую ячейку.

```python

import numpy as np

# Создание игрового поля

grid_world = np.array([

[0, 0, 0, 0], # Пустая ячейка

[0, -1, 0, -1], # Препятствие (-1)

[0, 0, 0, -1], # Препятствие (-1)

[0, -1, 0, 1] # Целевая ячейка (1)

])

```

Теперь создадим простое правило для агента: если агент находится в ячейке, он может выбирать случайное действие: двигаться вверх, вниз, влево или вправо. Если агент попадает в препятствие, он не двигается и остается на месте. Если агент достигает целевой ячейки, он получает награду +10 и игра завершается.

```python

import random

# Функция для выполнения действия в игре

def take_action(state):

row, col = state

if grid_world[row, col] == -1: # Если попали в препятствие, остаемся на месте

return state

action = random.choice(['up', 'down', 'left', 'right']) # Случайное действие

if action == 'up':

row = max(0, row – 1)

elif action == 'down':

row = min(grid_world.shape[0] – 1, row + 1)

elif action == 'left':

col = max(0, col – 1)

elif action == 'right':

col = min(grid_world.shape[1] – 1, col + 1)

return (row, col)

# Функция для проверки завершения игры и получения награды

def get_reward(state):

row, col = state

if grid_world[row, col] == 1: # Если достигли целевой ячейки

return 10, True

return 0, False # Игра продолжается

# Функция для запуска игры

def play_game():

state = (0, 0) # Начальное состояние агента

total_reward = 0

done = False

while not done:

state = take_action(state)

reward, done = get_reward(state)

total_reward += reward

return total_reward

# Запуск игры

total_reward = play_game()

print("Total reward:", total_reward)

```

Это простой пример задачи обучения с подкреплением, где агент играет в игру "Сетка мира", перемещаясь по полю и получая награду за достижение целевой ячейки.

Пример 2

Рассмотрим пример задачи с использованием обучения с подкреплением. Давайте представим симуляцию игры в кости, где агент должен научиться выбирать наилучшие действия (выбор числа от 1 до 6) для максимизации своего выигрыша.

```python

import numpy as np

class DiceGame:

def __init__(self):

self.state = 0 # текущее состояние – результат броска кости

self.done = False # флаг окончания игры

self.reward = 0 # награда за текущий шаг

def step(self, action):

# Выполняем действие – бросаем кость

self.state = np.random.randint(1, 7)

# Вычисляем награду

if action == self.state:

self.reward = 10 # выигрыш, если действие совпало с результатом броска

else:

self.reward = 0 # нет выигрыша

# Устанавливаем флаг окончания игры (игра заканчивается после одного хода)

self.done = True

return self.state, self.reward, self.done

def reset(self):

# Сбрасываем состояние игры для нового эпизода

self.state = 0

self.done = False

self.reward = 0

return self.state

# Пример простой стратегии выбора действий – всегда выбираем число 3

def simple_strategy(state):

return 3

# Основной код обучения с подкреплением

env = DiceGame()

total_episodes = 1000

learning_rate = 0.1

discount_rate = 0.99

q_table = np.zeros((6, 6)) # Q-таблица для хранения оценок ценности действий

for episode in range(total_episodes):

state = env.reset()

done = False

while not done:

action = simple_strategy(state)

next_state, reward, done = env.step(action)

# Обновление Q-таблицы по формуле Q(s,a) = Q(s,a) + α * (reward + γ * max(Q(s',a')) – Q(s,a))

q_table[state – 1, action – 1] += learning_rate * (reward + discount_rate * np.max(q_table[next_state – 1, :]) – q_table[state – 1, action – 1])

state = next_state

print("Q-таблица после обучения:")

print(q_table)

```

Этот код реализует простую симуляцию игры в кости и обновляет Q-таблицу на основе наград, полученных в процессе игры. Мы используем простую стратегию, всегда выбирая число 3. Однако, в реальных приложениях, агент мог бы изучать и выбирать действия на основе обучения Q-таблице, которая представляет собой оценку ценности различных действий в каждом состоянии.

Таким образом, таксономия задач машинного обучения помогает организовать разнообразие задач в соответствии с их основными характеристиками, что облегчает понимание и выбор подходящих методов и алгоритмов для решения конкретных задач.

1.3.2 Подробный анализ типов задач и подходов к их решению

В данном разделе мы проведем подробный анализ различных типов задач, с которыми сталкиваются специалисты в области машинного обучения, а также рассмотрим основные подходы к их решению.

1. Задачи классификации

Задачи классификации заключаются в присвоении объектам одной из заранее определенных категорий или классов на основе их характеристик. Некоторые основные методы решения задач классификации включают в себя:

– Логистическая регрессия

– Метод k ближайших соседей (k-NN)

– Метод опорных векторов (SVM)

– Деревья решений и их ансамбли (случайный лес, градиентный бустинг)

Рассмотрим каждый метод подробнее.

Логистическая регрессия:

Логистическая регрессия – это мощный метод в машинном обучении, который широко применяется для решения задач классификации, особенно в ситуациях, когда необходимо предсказать, принадлежит ли объект к одному из двух классов. Несмотря на название, логистическая регрессия на самом деле используется для бинарной классификации, где целевая переменная принимает одно из двух возможных значений.

Центральным элементом логистической регрессии является логистическая функция, также известная как сигмоидальная функция. Она преобразует линейную комбинацию признаков в вероятность принадлежности объекта к определенному классу. Это позволяет модели выдавать вероятности принадлежности к каждому классу, что делает ее особенно полезной для задач, требующих оценки уверенности в предсказаниях.

В процессе обучения логистическая регрессия настраивает параметры модели, минимизируя функцию потерь, такую как кросс-энтропия. Этот процесс обучения можно реализовать с использованием различных оптимизационных методов, таких как градиентный спуск.

Логистическая регрессия имеет несколько значительных преимуществ. Во-первых, она проста в интерпретации, что позволяет анализировать вклад каждого признака в принятие решения моделью. Кроме того, она эффективна в вычислении и хорошо масштабируется на большие наборы данных. Также важно отметить, что у логистической регрессии небольшое количество гиперпараметров, что упрощает процесс настройки модели.

Однако у логистической регрессии также есть свои ограничения. Во-первых, она предполагает линейную разделимость классов, что ограничивает ее способность моделировать сложные нелинейные зависимости между признаками. Кроме того, она чувствительна к выбросам и может давать непредсказуемые результаты в случае наличия значительного количества выбросов в данных. Тем не менее, при правильном использовании и учете этих ограничений, логистическая регрессия остается мощным инструментом для решения широкого спектра задач классификации.

Пример 1

Давайте представим, что у нас есть набор данных о покупках клиентов в интернет-магазине, и мы хотим предсказать, совершит ли клиент покупку на основе его предыдущих действий. Это может быть задача бинарной классификации, которую мы можем решить с помощью логистической регрессии.

Задача:

Наша задача – на основе информации о клиентах и их действиях на сайте (например, время проведенное на сайте, количество просмотренных страниц, наличие добавленных товаров в корзину и т. д.), предсказать, совершит ли клиент покупку или нет.

Решение:

Для решения задачи предсказания покупок клиентов в интернет-магазине мы использовали модель логистической регрессии. Это классический метод бинарной классификации, который подходит для таких задач, где требуется определить вероятность принадлежности объекта к одному из двух классов.

Сначала мы загрузили данные о клиентах из файла "customer_data.csv" с помощью библиотеки pandas. Этот набор данных содержал информацию о различных признаках клиентов, таких как время проведенное на сайте, количество просмотренных страниц, наличие добавленных товаров в корзину и другие. Кроме того, для каждого клиента было указано, совершил ли он покупку (целевая переменная).

Далее мы предварительно обработали данные, если это было необходимо, например, заполнили пропущенные значения или закодировали категориальные признаки. Затем мы разделили данные на обучающий и тестовый наборы с использованием функции `train_test_split` из библиотеки scikit-learn.

После этого мы создали и обучили модель логистической регрессии с помощью класса `LogisticRegression` из scikit-learn на обучающем наборе данных. Затем мы использовали обученную модель, чтобы сделать предсказания на тестовом наборе данных.

Наконец, мы оценили качество модели, вычислив метрики, такие как точность (`accuracy`), матрица ошибок (`confusion_matrix`) и отчет о классификации (`classification_report`). Эти метрики помогают нам понять, насколько хорошо модель справляется с поставленной задачей классификации и какие ошибки она допускает.

Таким образом, с помощью модели логистической регрессии мы можем предсказывать вероятность совершения покупки клиентом на основе его поведения на сайте, что может быть полезно для принятия решений о маркетинговых стратегиях, персонализации предложений и улучшении пользовательского опыта.

Код решения:

```python

import pandas as pd

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

# Загрузка данных

data = pd.read_csv("customer_data.csv")

# Предобработка данных

# Например, заполнение пропущенных значений, кодирование категориальных признаков и т.д.

# Разделение данных на обучающий и тестовый наборы

X = data.drop('purchase', axis=1) # признаки

y = data['purchase'] # целевая переменная

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Обучение модели логистической регрессии

model = LogisticRegression()

model.fit(X_train, y_train)

# Предсказание на тестовом наборе

y_pred = model.predict(X_test)

# Оценка качества модели

accuracy = accuracy_score(y_test, y_pred)

conf_matrix = confusion_matrix(y_test, y_pred)

class_report = classification_report(y_test, y_pred)

print("Accuracy:", accuracy)

print("Confusion Matrix:\n", conf_matrix)

print("Classification Report:\n", class_report)

```

Этот код загружает данные о клиентах, разделяет их на обучающий и тестовый наборы, обучает модель логистической регрессии на обучающем наборе, предсказывает целевую переменную на тестовом наборе и оценивает качество модели с помощью метрик, таких как точность, матрица ошибок и отчет о классификации.

Перед выполнением этого кода необходимо убедиться, что данные находятся в файле "customer_data.csv" и соответствуют описанной выше структуре. Кроме того, предварительная обработка данных (например, заполнение пропущенных значений, кодирование категориальных признаков) может потребоваться в зависимости от конкретного набора данных.

Метод k ближайших соседей (k-NN):

Метод k ближайших соседей (k-NN) представляет собой простой и интуитивно понятный алгоритм классификации, который основан на принципе "похожесть привлекает". Он оперирует идеей о том, что объекты, находящиеся близко в пространстве признаков, склонны принадлежать к одному и тому же классу.

В процессе классификации нового объекта алгоритм ищет k ближайших объектов в обучающем наборе данных, используя заданную метрику расстояния (например, евклидово расстояние). Затем он присваивает этому объекту класс, который наиболее часто встречается среди соседей (например, с помощью голосования).

Одним из основных преимуществ метода k-NN является его простота и интуитивная понятность. Он не требует сложной предварительной обработки данных или параметров для обучения во время этапа обучения, что делает его привлекательным для быстрого прототипирования и начального анализа данных. Кроме того, k-NN хорошо работает на небольших наборах данных и может быть эффективным в задачах с небольшим числом классов.

Однако у метода k-NN есть и недостатки. Во-первых, он может быть вычислительно затратным, особенно при большом количестве объектов в обучающем наборе данных, поскольку требуется вычисление расстояний до всех объектов. Кроме того, к-NN чувствителен к выбросам и шуму в данных, так как классификация нового объекта зависит от близости к соседям, и наличие выбросов может привести к неправильной классификации.

В целом, метод k ближайших соседей остается полезным инструментом в арсенале алгоритмов машинного обучения, особенно в случае небольших наборов данных и когда требуется быстрое решение задачи классификации без сложной предварительной настройки. Однако необходимо учитывать его ограничения и применять его с осторожностью в случае больших объемов данных или данных с выбросами.

Пример 1

Задача:

Представим, что у нас есть набор данных о студентах, включающий их оценки за различные учебные предметы, а также информацию о других характеристиках, таких как время, проведенное за учебой, уровень учебной мотивации и т.д. Наша задача состоит в том, чтобы предсказать, будет ли студент успешно сдавать экзамен по математике (например, получит оценку выше 70 баллов) на основе этих данных.