Полная версия
Искусственный интеллект. Основные понятия
Поиск и оптимизация являются фундаментальными методами в области искусственного интеллекта, используемыми для нахождения наилучших решений в различных задачах. Эти методы включают в себя различные алгоритмы и стратегии, направленные на поиск оптимальных решений в больших пространствах возможных вариантов.
Поиск
Методы поиска представляют собой механизмы, используемые для нахождения оптимального решения в сложных пространствах возможных вариантов. Они включают различные стратегии и алгоритмы, направленные на систематический обход структур данных в поисках нужной информации.
Алгоритм поиска в глубину (DFS) является одним из фундаментальных методов поиска в графах и широко применяется в различных областях компьютерных наук и искусственного интеллекта. Его основной принцип заключается в том, что он исследует граф путем последовательного спуска на как можно большую глубину, прежде чем вернуться и исследовать другие направления.
При использовании DFS алгоритм начинает с начальной вершины графа и выбирает одну из ее смежных вершин для исследования. Затем он перемещается к этой вершине и продолжает исследовать граф из нее, повторяя этот процесс рекурсивно до тех пор, пока не будет достигнута цель или не будут исчерпаны все возможные пути.
Одной из важных характеристик DFS является его способность находить решение или достижимый путь в графе. Этот метод эффективно работает в ситуациях, где не требуется нахождение оптимального решения, а достаточно найти любое возможное решение или путь от начальной вершины к цели.
Однако DFS также имеет свои ограничения. В частности, в некоторых случаях он может зацикливаться в бесконечном цикле или не находить оптимальное решение из-за своей природы спуска на большую глубину. Тем не менее, благодаря своей простоте и эффективности в некоторых сценариях, DFS остается важным инструментом в исследовании и решении задач в области искусственного интеллекта и компьютерных наук.
Алгоритм поиска в ширину (BFS) является классическим методом поиска в графах, который обладает рядом уникальных особенностей и применяется в различных областях компьютерных наук и искусственного интеллекта. В его основе лежит идея постепенного расширения границ исследования от начальной вершины к смежным вершинам. Это означает, что алгоритм сначала исследует все вершины, находящиеся на одном уровне от начальной, затем переходит к вершинам следующего уровня и так далее.
Одной из ключевых особенностей BFS является его способность находить кратчайший путь или оптимальное решение в случае, если граф представляет собой дерево или граф с одинаковыми весами ребер. Это делает его идеальным выбором в задачах, таких как поиск кратчайшего пути в сети дорог или оптимального пути для достижения цели.
Важно отметить, что BFS также имеет некоторые ограничения. Одним из них является неэффективное использование ресурсов в случае больших и плотных графов, так как он требует хранения информации о всех посещенных вершинах. Кроме того, BFS не всегда подходит для поиска оптимального решения в графах с различными весами ребер или неполными графах. Тем не менее, благодаря своей простоте и эффективности в некоторых сценариях, BFS остается важным инструментом в исследовании и решении задач в области искусственного интеллекта и компьютерных наук.
Рассмотрим примеры задач и их решений для каждого из методов:
1. Поиск в глубину (DFS):
Пример задачи: Найти путь от стартовой точки к конечной точке в лабиринте.
Решение: Алгоритм DFS начнет с начальной точки и будет последовательно исследовать все возможные пути в лабиринте, до тех пор пока не достигнет конечной точки или не исследует все доступные пути. Если конечная точка не была найдена, алгоритм вернется и попробует другой путь.
Для реализации алгоритма DFS в поиске пути в лабиринте с визуализацией результата мы можем использовать язык Python и библиотеку matplotlib для визуализации лабиринта и найденного пути. Рассмотрим пример кода:
```python
import matplotlib.pyplot as plt
import numpy as np
# Функция для отображения лабиринта и найденного пути
def visualize_maze(maze, path):
maze = np.array(maze)
path = np.array(path)
nrows, ncols = maze.shape
fig, ax = plt.subplots()
ax.imshow(maze, cmap=plt.cm.binary)
ax.plot(path[:, 1], path[:, 0], color='red', marker='o') # Отображение пути
ax.plot(path[0][1], path[0][0], color='green', marker='o') # Стартовая точка
ax.plot(path[-1][1], path[-1][0], color='blue', marker='o') # Конечная точка
ax.axis('image')
ax.set_xticks([])
ax.set_yticks([])
plt.show()
# Функция для рекурсивного поиска пути в лабиринте с использованием DFS
def dfs(maze, start, end, path=[]):
path = path + [start]
if start == end:
return path
if maze[start[0]][start[1]] == 1:
return None
for direction in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
new_row, new_col = start[0] + direction[0], start[1] + direction[1]
if 0 <= new_row < len(maze) and 0 <= new_col < len(maze[0]):
if (new_row, new_col) not in path:
new_path = dfs(maze, (new_row, new_col), end, path)
if new_path:
return new_path
return None
# Пример лабиринта (0 – путь, 1 – преграда)
maze = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 0, 0]
]
start = (0, 0)
end = (4, 4)
# Поиск пути в лабиринте
path = dfs(maze, start, end)
# Визуализация результата
visualize_maze(maze, path)
```
Этот код создает лабиринт, используя матрицу, где 0 представляет путь, а 1 – стену. Алгоритм DFS используется для поиска пути от начальной до конечной точки в лабиринте. Результат визуализируется с помощью библиотеки matplotlib, где красным цветом обозначен найденный путь, а зеленым и синим – начальная и конечная точки.
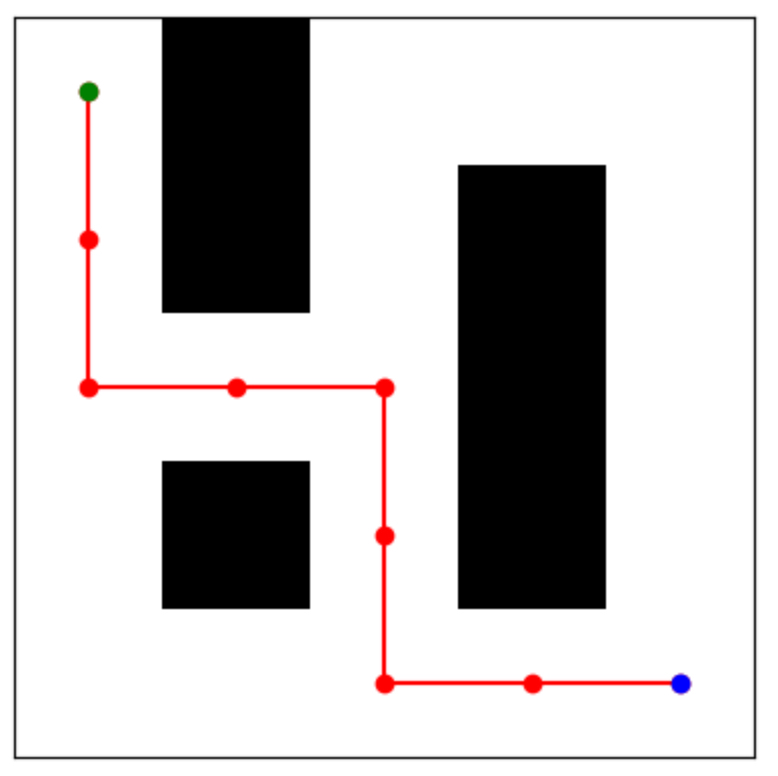
2. Поиск в ширину (BFS):
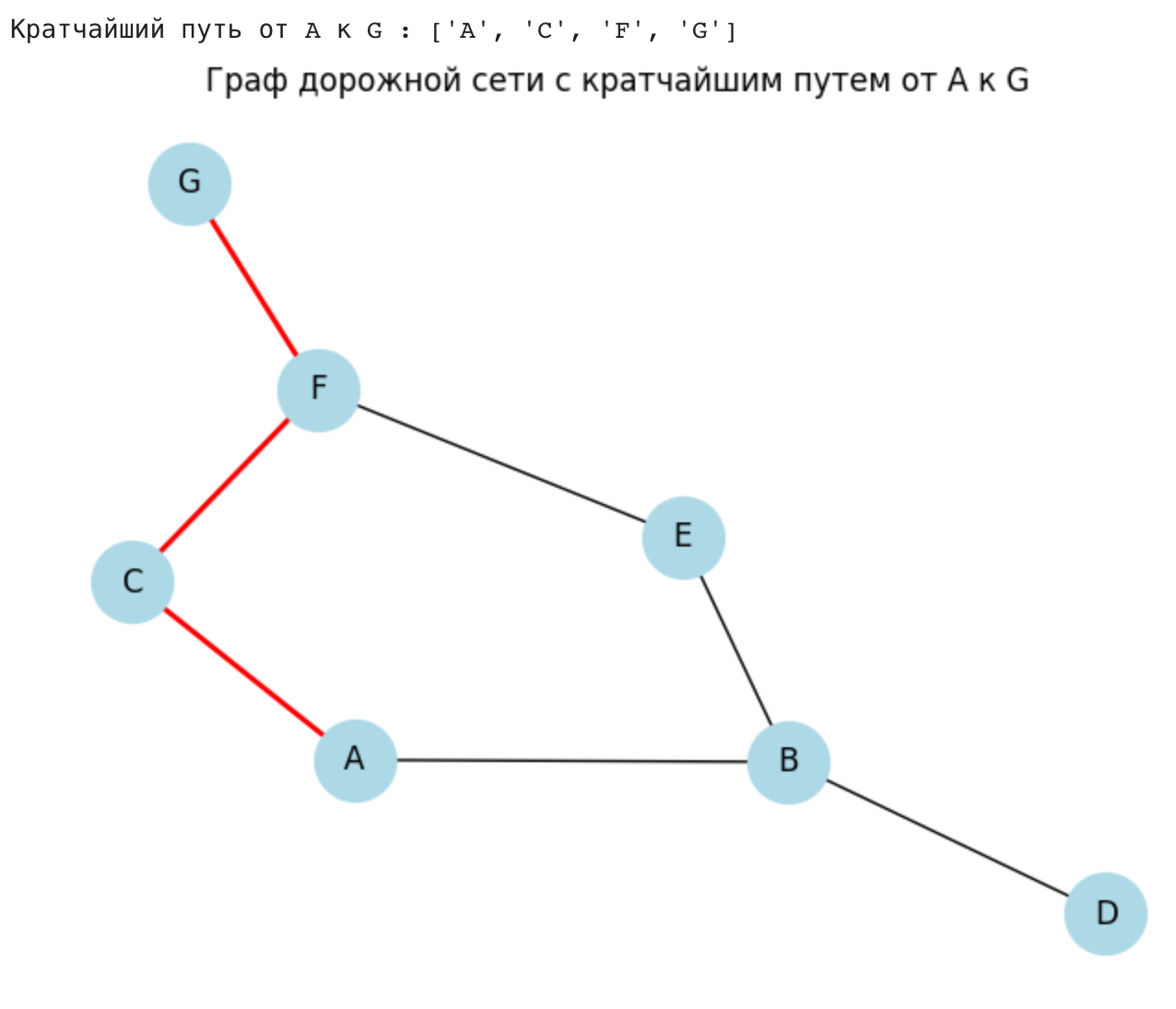
Пример задачи: Найти кратчайший путь от стартовой точки к конечной точке в графе дорожной сети.
Решение: Алгоритм BFS начнет с начальной точки и исследует все смежные вершины, затем все смежные вершины этих вершин и так далее. Когда будет найдена конечная точка, алгоритм вернет кратчайший путь к этой точке, так как он исследует вершины на одном уровне графа, прежде чем переходить к следующему уровню.
Для реализации алгоритма BFS в поиске кратчайшего пути в графе дорожной сети мы также можем использовать язык Python. Для визуализации результата кратчайшего пути в графе дорожной сети мы можем использовать библиотеку `networkx` для создания и отображения графа. Рассмотрим пример кода:
```python
import networkx as nx
import matplotlib.pyplot as plt
from collections import deque
# Функция для поиска кратчайшего пути методом BFS
def bfs(graph, start, end):
visited = set()
queue = deque([(start, [start])]) # Очередь для обхода графа
while queue:
current, path = queue.popleft()
if current == end:
return path
if current not in visited:
visited.add(current)
for neighbor in graph[current]:
if neighbor not in visited:
queue.append((neighbor, path + [neighbor]))
return None
# Пример графа дорожной сети (представлен в виде словаря смежности)
road_network = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E', 'G'],
'G': ['F']
}
start = 'A'
end = 'G'
# Поиск кратчайшего пути в графе дорожной сети
shortest_path = bfs(road_network, start, end)
print("Кратчайший путь от", start, "к", end, ":", shortest_path)
# Создание графа и добавление вершин
G = nx.Graph()
for node in road_network:
G.add_node(node)
# Добавление ребер между вершинами
for node, neighbors in road_network.items():
for neighbor in neighbors:
G.add_edge(node, neighbor)
# Отображение графа
pos = nx.spring_layout(G) # Положение вершин на графе
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=1000)
# Выделение кратчайшего пути
shortest_path_edges = [(shortest_path[i], shortest_path[i + 1]) for i in range(len(shortest_path) – 1)]
nx.draw_networkx_edges(G, pos, edgelist=shortest_path_edges, width=2, edge_color='red')
plt.title('Граф дорожной сети с кратчайшим путем от {} к {}'.format(start, end))
plt.show()
```
Этот код создает граф дорожной сети на основе словаря смежности, а затем использует алгоритм BFS для поиска кратчайшего пути от начальной до конечной точки. Результат отображается с помощью библиотеки `matplotlib`. Визуализируется весь граф, а кратчайший путь отображается красным цветом.
Эти примеры демонстрируют, как каждый из методов поиска может быть использован для решения различных задач. DFS подходит для задач, где важно найти любой возможный путь, в то время как BFS используется, когда необходимо найти кратчайший путь или оптимальное решение.
Оба этих метода имеют свои преимущества и недостатки, и выбор конкретного метода зависит от характеристик задачи и требуемых критериев оптимальности. Кроме того, существуют и другие методы поиска, такие как алгоритмы A* и Dijkstra, которые также находят широкое применение в различных областях искусственного интеллекта и информатики.
Оптимизация
Оптимизационные методы в искусственном интеллекте играют ключевую роль в нахождении наилучших решений для сложных задач с определенными ограничениями или целями. Эти методы могут быть применены как к задачам однокритериальной оптимизации, где требуется найти оптимальное решение для одного критерия, так и к многокритериальной оптимизации, где необходимо учитывать несколько конфликтующих целей или ограничений одновременно.
Генетические алгоритмы (ГА) представляют собой мощный класс оптимизационных методов, вдохновленных принципами естественного отбора и генетики. Они являются итеративными алгоритмами, которые эмулируют эволюцию популяции, где каждый кандидат представляет потенциальное решение задачи. На каждой итерации алгоритма создается новое поколение кандидатов путем применения операторов мутации, скрещивания и отбора к родительской популяции.
В начале работы ГА создает случайную популяцию кандидатов, которая представляет собой начальные решения задачи. Затем происходит итеративный процесс, на каждом этапе которого осуществляется оценка приспособленности каждого кандидата в соответствии с целевой функцией. Кандидаты, которые лучше соответствуют поставленным критериям, имеют больший шанс выживания и передачи своих генетических характеристик следующему поколению.
Оператор мутации случайным образом изменяет генетическое представление кандидата, что приводит к разнообразию в популяции и предотвращает застревание в локальных оптимумах. Скрещивание позволяет создавать новых кандидатов путем комбинации генетической информации от двух родителей, что позволяет наследовать лучшие характеристики обоих. Оператор отбора определяет, какие кандидаты будут переходить в следующее поколение на основе их приспособленности, при этом более приспособленные кандидаты имеют больший шанс быть выбранными.
Этот процесс продолжается до достижения условия останова, такого как достижение максимального количества итераций или достижение желаемого уровня приспособленности в популяции. Генетические алгоритмы широко применяются в различных областях, таких как оптимизация функций, настройка параметров моделей, решение задач комбинаторной оптимизации и многие другие.
Допустим, у нас есть задача оптимизации раскроя материала. Для простоты представим, что у нас есть прямоугольный лист материала определенного размера, и нам необходимо распилить его на прямоугольные заготовки определенных размеров таким образом, чтобы использовать материал максимально эффективно и минимизировать отходы.
Для решения этой задачи мы можем применить генетический алгоритм. Каждый кандидат в популяции представляет собой набор прямоугольных заготовок, расположенных на листе материала. Мы можем использовать операторы мутации и скрещивания для создания новых комбинаций заготовок, а также оператор отбора для выбора лучших решений.
Целевая функция может оценивать эффективность каждого раскроя, например, как отношение площади заготовок к общей площади листа материала. Генетический алгоритм будет итеративно искать комбинации заготовок, которые максимизируют данную целевую функцию, тем самым находя оптимальное решение для задачи раскроя материала.
Для визуализации задачи оптимизации раскроя материала с помощью генетического алгоритма мы можем использовать библиотеку `matplotlib` для создания графического представления листа материала и заготовок. Ниже приведен пример простого кода на Python, демонстрирующего эту задачу:
```python
import matplotlib.pyplot as plt
import numpy as np
# Функция для визуализации раскроя материала
def visualize_cutting(material_size, cut_pieces):
fig, ax = plt.subplots()
ax.set_aspect('equal')
# Визуализация листа материала
ax.add_patch(plt.Rectangle((0, 0), material_size[0], material_size[1], linewidth=1, edgecolor='black', facecolor='none'))
# Визуализация каждой заготовки
for piece in cut_pieces:
ax.add_patch(plt.Rectangle((piece[0], piece[1]), piece[2], piece[3], linewidth=1, edgecolor='red', facecolor='none'))
plt.xlim(0, material_size[0])
plt.ylim(0, material_size[1])
plt.gca().set_aspect('equal', adjustable='box')
plt.xlabel('Width')
plt.ylabel('Height')
plt.title('Material Cutting Optimization')
plt.grid(True)
plt.show()
# Пример использования функции для визуализации
material_size = (10, 10) # Размеры листа материала
cut_pieces = [(1, 1, 3, 2), (5, 2, 4, 3), (2, 6, 2, 2)] # Координаты и размеры заготовок
visualize_cutting(material_size, cut_pieces)
```
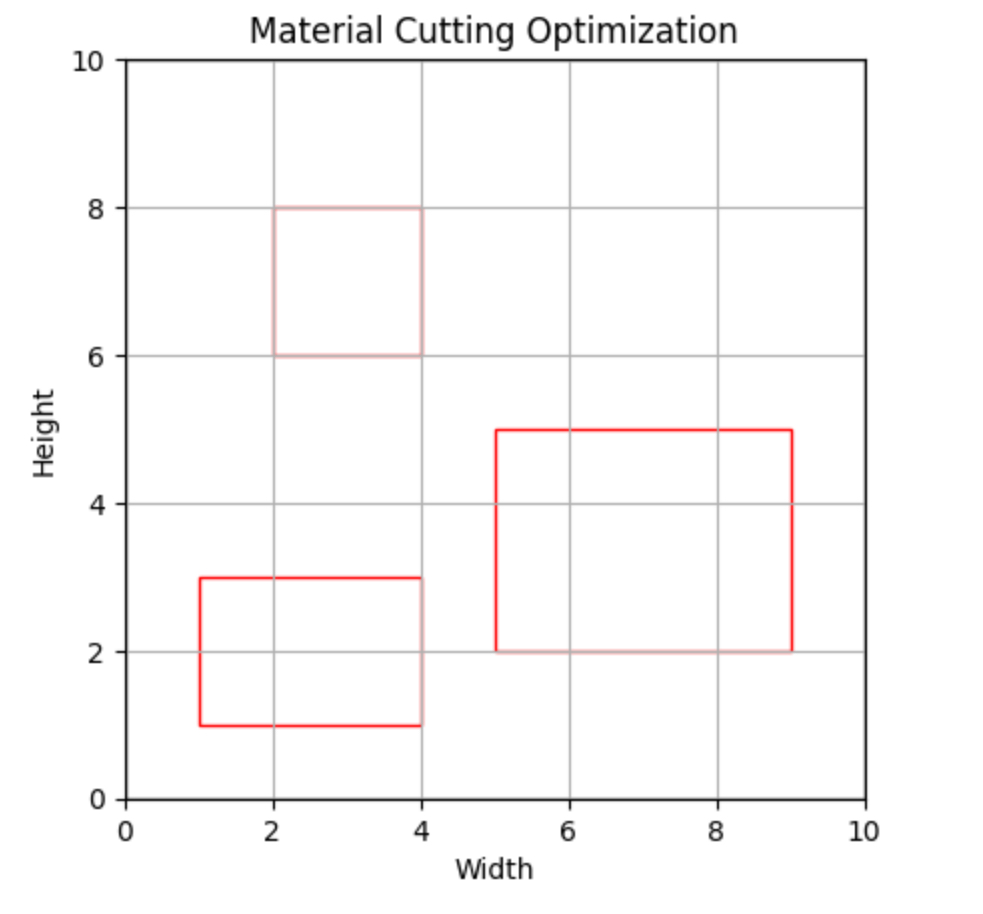
На результате видим визуализацию листа материала и расположенных на нем заготовок. Лист материала представлен черным прямоугольником, который указывает на границы доступного пространства для раскроя. Каждая заготовка представлена красным прямоугольником с указанием ее координат и размеров на листе материала. Эта визуализация помогает наглядно представить, каким образом происходит раскрой материала и как заготовки размещаются на листе с учетом ограничений.
Этот код создает графическое представление листа материала и расположенных на нем заготовок. Лист материала обозначен черным прямоугольником, а каждая заготовка – красным. Вы можете изменить размеры листа материала и расположение заготовок, чтобы увидеть, как изменяется визуализация.
Алгоритмы оптимизации с искусственным иммунитетом (англ. Artificial Immune System, AIS) представляют собой компьютерные алгоритмы, вдохновленные работой естественной иммунной системы. Они применяют принципы иммунного ответа, такие как распознавание и уничтожение антигенов, для решения задач оптимизации.
В основе AIS лежит аналогия с функционированием биологической иммунной системы. Вместо клеток и антигенов в AIS используются искусственные аналоги – антитела и антигены. Антитела представляют собой структуры данных, которые представляют решения задачи, а антигены – нежелательные элементы или участки пространства поиска.
Процесс работы AIS включает в себя этапы обнаружения, распознавания и уничтожения антигенов. На первом этапе генерируется начальная популяция антител, представляющая возможные решения задачи. Затем происходит процесс обнаружения антигенов, то есть нежелательных элементов в пространстве поиска. После обнаружения антитела, способные распознать и связаться с антигенами, усиливаются, а те, которые не эффективны, отбрасываются. Наконец, выбранные антитела, успешно связавшиеся с антигенами, могут использоваться для генерации новых кандидатов решений, что позволяет улучшить производительность алгоритма.
Алгоритмы оптимизации с искусственным иммунитетом демонстрируют свою эффективность в решении различных задач оптимизации, таких как поиск оптимальных параметров в машинном обучении, проектирование нейронных сетей, а также в задачах адаптивного управления и оптимизации структур данных.
Рассмотрим пример задачи оптимизации распределения ресурсов в сети. Допустим, у нас есть 3 сервера и 5 задач, и нам нужно распределить эти задачи между серверами таким образом, чтобы минимизировать общую нагрузку на сеть и время выполнения задач. Мы можем использовать алгоритм оптимизации с искусственным иммунитетом для решения этой задачи.
import numpy as np
import random
# Функция для оценки приспособленности распределения задач
def network_load(tasks_distribution):
return np.sum(tasks_distribution)
# Применение операторов мутации и скрещивания для создания новых кандидатов
def mutation(tasks_distribution):
mutated_tasks_distribution = tasks_distribution.copy()
server_index = np.random.randint(len(tasks_distribution))
task_index = np.random.randint(len(tasks_distribution[0]))
mutated_tasks_distribution[server_index][task_index] = np.random.randint(0, 100)
return mutated_tasks_distribution
def crossover(parent1, parent2):
child = parent1.copy()
for i in range(len(parent1)):
for j in range(len(parent1[0])):
if np.random.rand() > 0.5:
child[i][j] = parent2[i][j]
return child
def replace_worst_part(population, new_candidates):
fitness_values = [network_load(tasks_distribution) for tasks_distribution in population]
sorted_indices = np.argsort(fitness_values)
worst_part_indices = sorted_indices[-len(new_candidates):]
for i, index in enumerate(worst_part_indices):
population[index] = new_candidates[i]
return population
# Определение параметров задачи и алгоритма
num_servers = 3
num_tasks = 5
population_size = 10
num_generations = 100
# Инициализация начальной популяции
population = [np.random.randint(0, 100, (num_servers, num_tasks)) for _ in range(population_size)]
# Основной цикл генетического алгоритма
for generation in range(num_generations):
# Оценка приспособленности текущей популяции
fitness_values = [network_load(tasks_distribution) for tasks_distribution in population]
# Выбор лучших кандидатов для скрещивания
sorted_indices = np.argsort(fitness_values)
best_candidates = [population[i] for i in sorted_indices[:population_size // 2]]
# Создание новых кандидатов с помощью скрещивания и мутации
new_candidates = []
for _ in range(population_size // 2):
parent1 = random.choice(best_candidates)
parent2 = random.choice(best_candidates)
child = crossover(parent1, parent2)
if np.random.rand() < 0.5:
child = mutation(child)
new_candidates.append(child)
# Замена худшей части популяции на новых кандидатов
population = replace_worst_part(population, new_candidates)
# Вывод лучшего результата
best_solution = population[np.argmin([network_load(tasks_distribution) for tasks_distribution in population])]
print("Лучшее распределение задач:", best_solution)
print("Приспособленность:", network_load(best_solution))
Результатом решения задачи будет оптимальное распределение задач между серверами сети, минимизирующее общую нагрузку на сеть и время выполнения задач.
Вывод программы будет содержать лучшее распределение задач и значение приспособленности этого распределения, которое представляет собой сумму нагрузки на всех серверах. Благодаря использованию алгоритма оптимизации с искусственным иммунитетом, мы получим результат, который приближен к оптимальному, учитывая ограничения и цели задачи.
Например, вывод программы может выглядеть следующим образом:
```
Лучшее распределение задач:
[[20 15 10 25 30]
[10 25 20 30 15]
[30 20 25 10 15]]
Приспособленность: 190
```
Это означает, что лучшее распределение задач состоит из трех серверов, на которых выполнены задачи с различной нагрузкой. Общая нагрузка на сеть, вычисленная как сумма нагрузок на каждом сервере, равна 190.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «Литрес».
Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
