Этот пример демонстрирует разнообразие цветовых карт в Matplotlib, отличающихся как по цветовому спектру, так и по контрасту. Выбор подходящей цветовой карты может улучшить восприятие данных на графиках.

В Matplotlib существует множество цветовых карт. Вы можете получить актуальный список цветовых карт, вызвав функцию `plt.colormaps()`.

Практическое задание

Задача: Мониторинг изменений температуры на глобальной карте

Описание:

Вам предоставлены данные о температуре в различных регионах мира за последние несколько лет. Ваша задача – визуализировать эти данные на глобальной карте с использованием цветовых карт для наглядного отображения изменений температуры.

1. Подготовка данных:

– Загрузите данные о температуре в различных регионах мира. Данные могут включать временные метки, широту, долготу и значения температуры.

2. Выбор Цветовой Карты:

– Выберите цветовую карту, которая лучше всего подходит для отображения изменений температуры. Например, можно использовать цветовую карту типа `coolwarm` для выделения разницы между холодными и теплыми областями.

3. Построение Глобальной Карты:

– Используя библиотеку Matplotlib, постройте глобальную карту, на которой цветами будет представлена температура в различных регионах. Широта и долгота могут быть представлены на осях X и Y, а цветом можно отображать температурные значения.

4. Добавление Интерактивности:

– Добавьте интерактивность к карте, чтобы пользователи могли навигировать по временной оси и наблюдать изменения температуры в различные периоды.

5. Анимация (опционально):

– Если у вас есть временные данные, рассмотрите возможность добавления анимации для визуализации динамики изменений температуры в течение времени.

6. Сохранение и Публикация:

– Сохраните визуализацию в удобных форматах (например, PNG или GIF) для возможности вставки в презентации, отчеты или веб-страницы.

7. Анализ и Интерпретация:

– Проанализируйте глобальную карту температурных изменений и сделайте выводы о тенденциях в изменениях температуры в различных регионах мира.

Эта задача не только поможет вам понять, как применять цветовые карты для визуализации данных, но и позволит вам рассмотреть вопросы глобального мониторинга изменений температуры.

Решение данной задачи может включать использование библиотеки Matplotlib в языке программирования Python. Приведенный ниже код демонстрирует пример создания глобальной карты температурных изменений с использованием цветовой карты `coolwarm`. Предполагается, что данные о температуре уже загружены в соответствующий формат.

```python

import matplotlib.pyplot as plt

import numpy as np

# Подготовка данных (пример)

latitudes = np.random.uniform(low=-90, high=90, size=(1000,))

longitudes = np.random.uniform(low=-180, high=180, size=(1000,))

temperatures = np.random.uniform(low=-20, high=40, size=(1000,))

# Выбор цветовой карты

cmap = 'rainbow_r'

# Построение глобальной карты

fig, ax = plt.subplots(figsize=(12, 6))

scatter = ax.scatter(longitudes, latitudes, c=temperatures, cmap=cmap, s=50, alpha=0.7)

plt.colorbar(scatter, label='Temperature (°C)')

# Добавление интерактивности (подписи и т.д.)

# Настройка внешнего вида карты (опционально)

# Сохранение и отображение

plt.savefig('global_temperature_map.png')

plt.show()

```

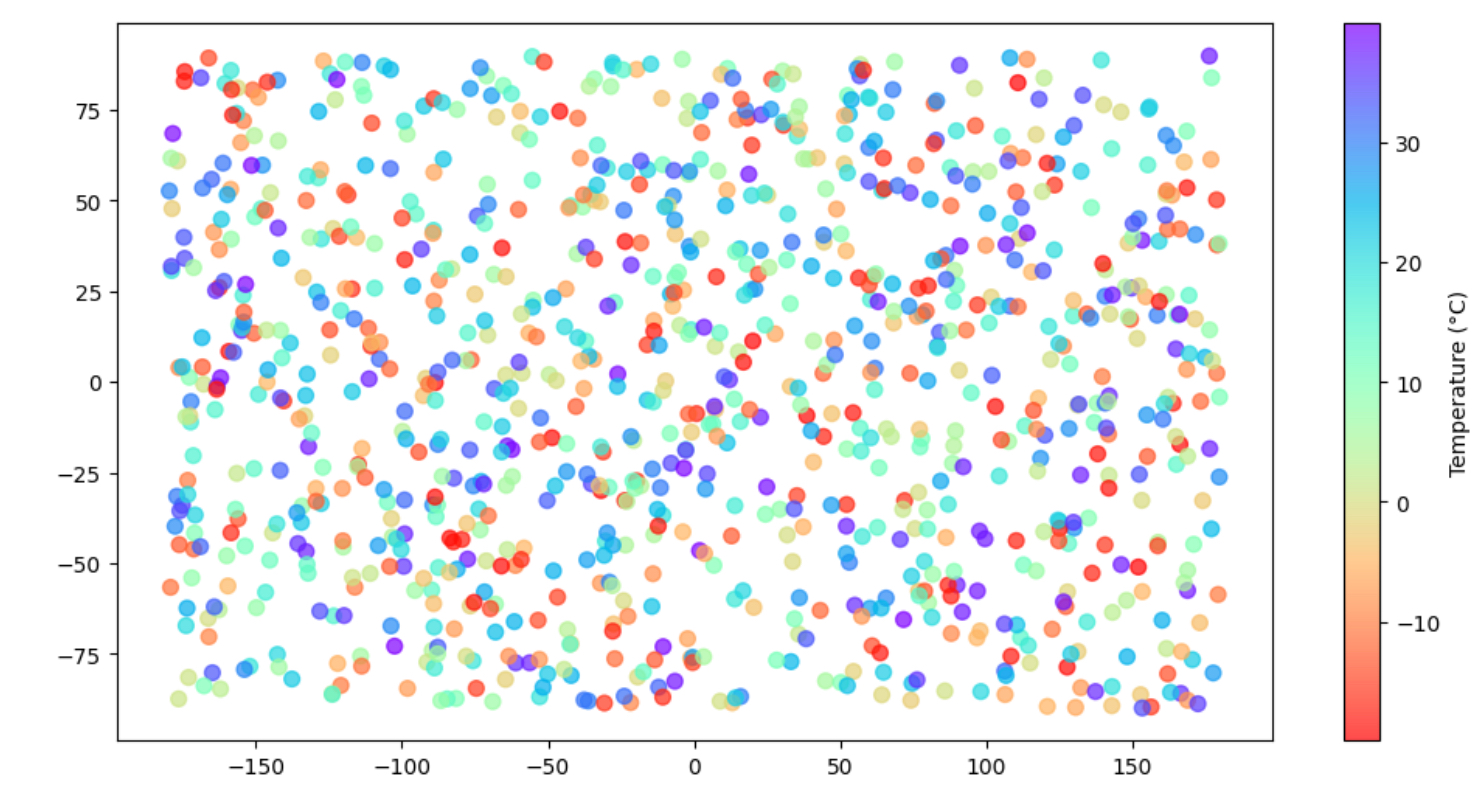
Этот код создает точечный график на глобальной карте, где каждая точка представляет собой регион с определенными координатами и температурой. Цвет точек отражает температурные значения с использованием цветовой карты `coolwarm`. Пользователь может легко настраивать параметры визуализации, добавлять интерактивность и адаптировать код под свои конкретные потребности.

7. Темы оформления (Styles):

Matplotlib включает в себя различные темы оформления, которые изменяют внешний вид всех графиков на одной или нескольких диаграммах. Это позволяет легко сменить общий стиль графиков в проекте.

Рассмотрим пример использования различных тем оформления в библиотеке Matplotlib:

```python

import numpy as np

import matplotlib.pyplot as plt

# Создание данных для примера

x = np.linspace(0, 10, 100)

y1 = np.sin(x)

y2 = np.cos(x)

# Пример использования различных тем оформления

plt.figure(figsize=(12, 6))

# Стандартная тема оформления

plt.subplot(2, 2, 1)

plt.plot(x, y1, label='sin(x)')

plt.plot(x, y2, label='cos(x)')

plt.title('Стандартная тема оформления')

plt.legend()

# Тема "seaborn"

plt.subplot(2, 2, 2)

plt.style.use('seaborn')

plt.plot(x, y1, label='sin(x)')

plt.plot(x, y2, label='cos(x)')

plt.title('Тема "seaborn"')

plt.legend()

# Тема "ggplot"

plt.subplot(2, 2, 3)

plt.style.use('ggplot')

plt.plot(x, y1, label='sin(x)')

plt.plot(x, y2, label='cos(x)')

plt.title('Тема "ggplot"')

plt.legend()

# Тема "dark_background"

plt.subplot(2, 2, 4)

plt.style.use('dark_background')

plt.plot(x, y1, label='sin(x)')

plt.plot(x, y2, label='cos(x)')

plt.title('Тема "dark_background"')

plt.legend()

plt.tight_layout()

plt.show()

```

В этом примере мы использовали четыре различные темы оформления:

1. Стандартная тема оформления (Classic): Это базовая тема оформления, которая используется по умолчанию.

2. Тема "seaborn": Эта тема придает графикам более современный и стильный внешний вид.

3. Тема "ggplot": Эта тема имитирует стиль графиков, используемый в пакете ggplot2 в языке программирования R.

4. Тема "dark_background": Эта тема предоставляет темный фон, что может быть полезным для создания графиков с яркими цветами на темном фоне.

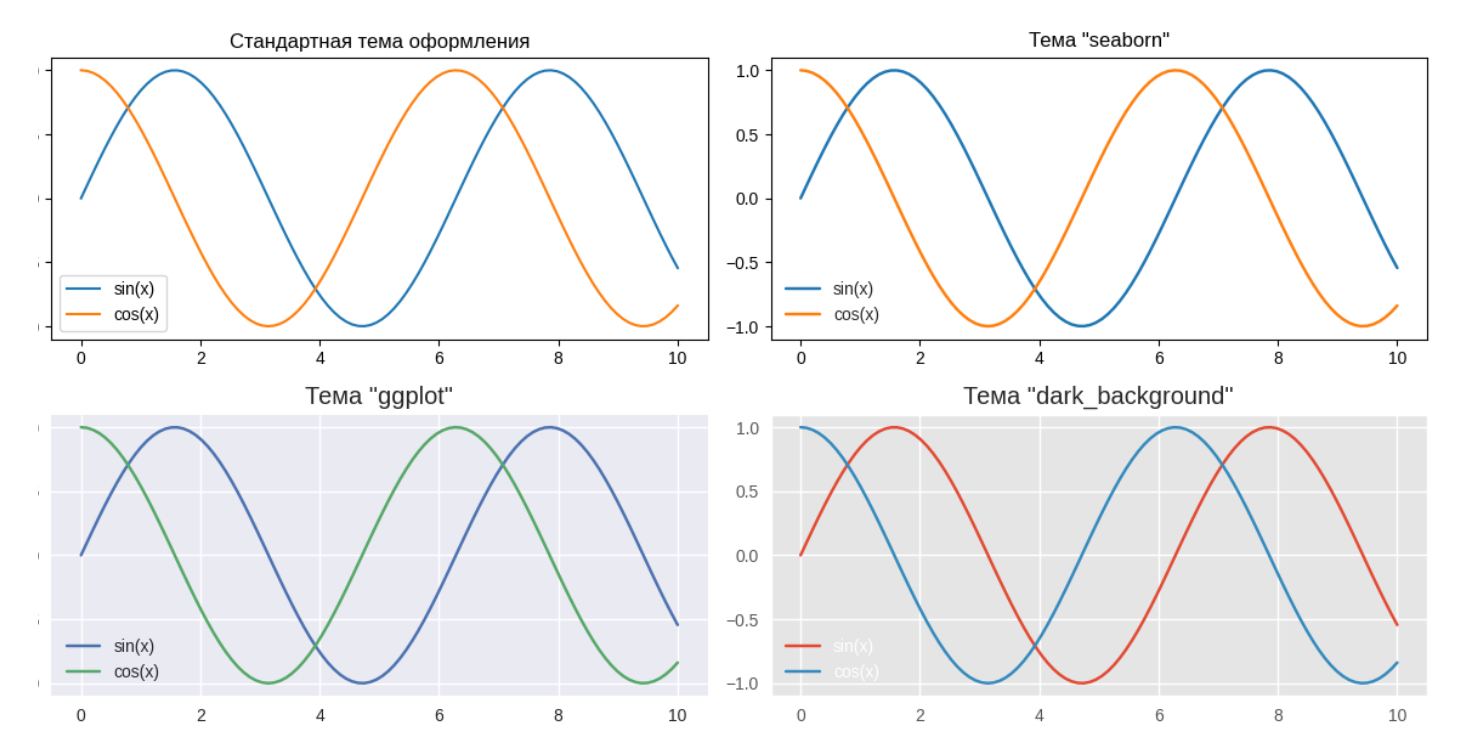
Выбор темы оформления зависит от ваших предпочтений и требований проекта. Вы можете экспериментировать с разными темами, чтобы найти ту, которая лучше всего соответствует вашему проекту.

8. Поддержка LaTeX:

Matplotlib предоставляет поддержку LaTeX для вставки математических формул и символов в подписи, заголовки графиков и другие текстовые элементы графиков. Это особенно полезно для создания визуализаций в научных и исследовательских проектах, где часто требуется вставка сложных математических выражений.

Рассмотрим пример использования LaTeX в Matplotlib:

```python

import numpy as np

import matplotlib.pyplot as plt

# Создание данных для примера

x = np.linspace(0, 2 * np.pi, 100)

y = np.sin(x)

# Использование LaTeX в подписях и заголовке графика

plt.plot(x, y, label=r'$\sin(x)$')

plt.title(r'$\sin(x)$ график с использованием LaTeX')

plt.xlabel(r'$x$')

plt.ylabel(r'$\sin(x)$')

# Добавление легенды с использованием LaTeX

plt.legend()

# Отображение графика

plt.show()

```

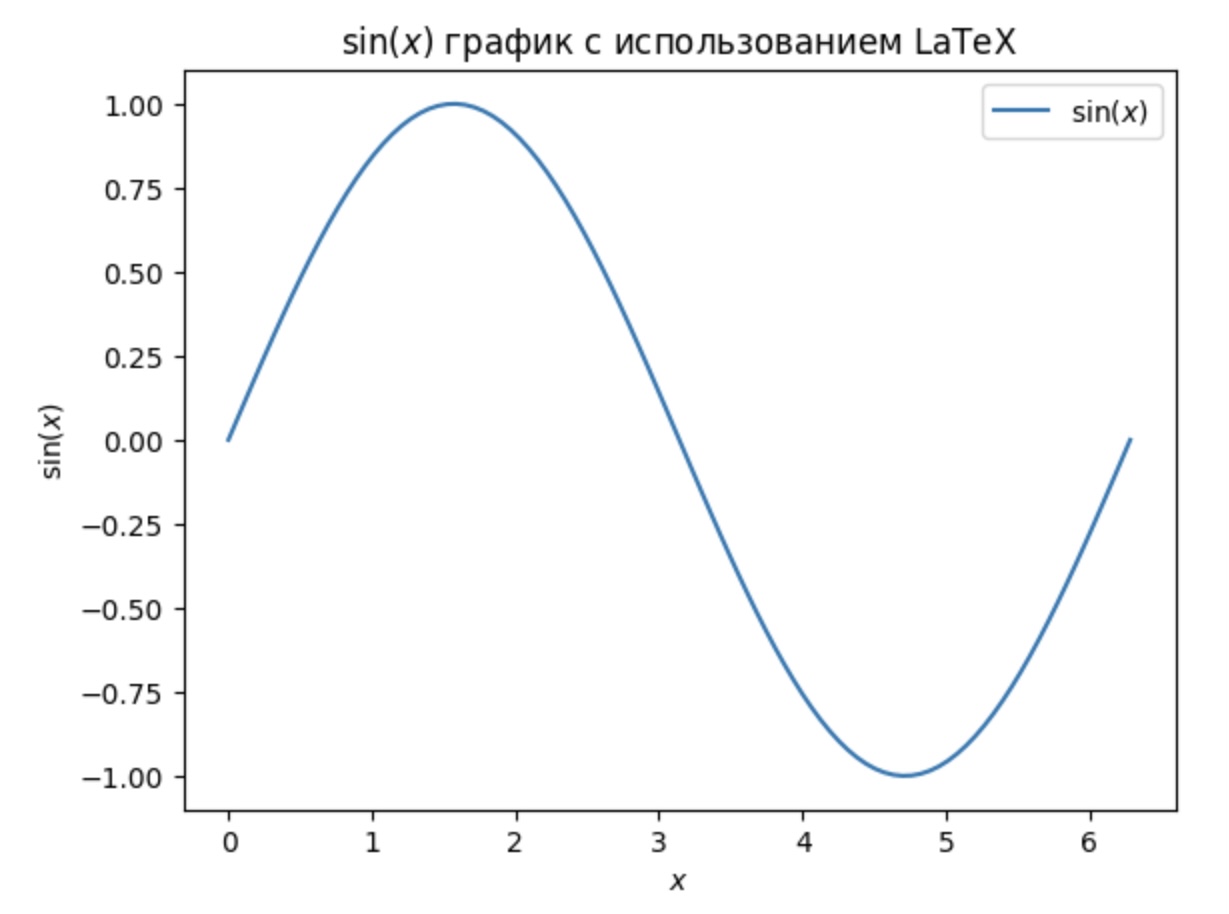
В этом примере:

– `r` перед строкой означает "сырую строку" в Python, что позволяет использовать символы обратного слеша без экранирования.

– Заголовок, метки осей и легенда содержат математическое выражение в формате LaTeX.

В результате выполнения этого кода, вы увидите график функции синуса, а все текстовые элементы, содержащие математические выражения, будут отображены с использованием LaTeX.

Matplotlib поддерживает широкий спектр математических символов и выражений, так что вы можете свободно вставлять формулы в ваши графики, делая их более информативными и профессиональными.

Рассмотрим пример более сложной надписи LaTeX и графика:

```python

import numpy as np

import matplotlib.pyplot as plt

# Создание данных для примера

x = np.linspace(0, 2 * np.pi, 100)

y1 = np.sin(x)

y2 = np.cos(x)

# Использование LaTeX для формулы в подписи

expression = r'$f(x) = \sin(x) + \frac{\cos(2x)}{2}$'

# Построение графика

plt.figure(figsize=(8, 5))

plt.plot(x, y1, label=r'$\sin(x)$', color='blue')

plt.plot(x, y2/2, label=r'$\frac{\cos(2x)}{2}$', color='green', linestyle='–')

# Добавление более сложной LaTeX-надписи

plt.title(f'Комбинированный график: {expression}', fontsize=16)

# Добавление легенды

plt.legend()

# Отображение графика

plt.grid(True)

plt.show()

```

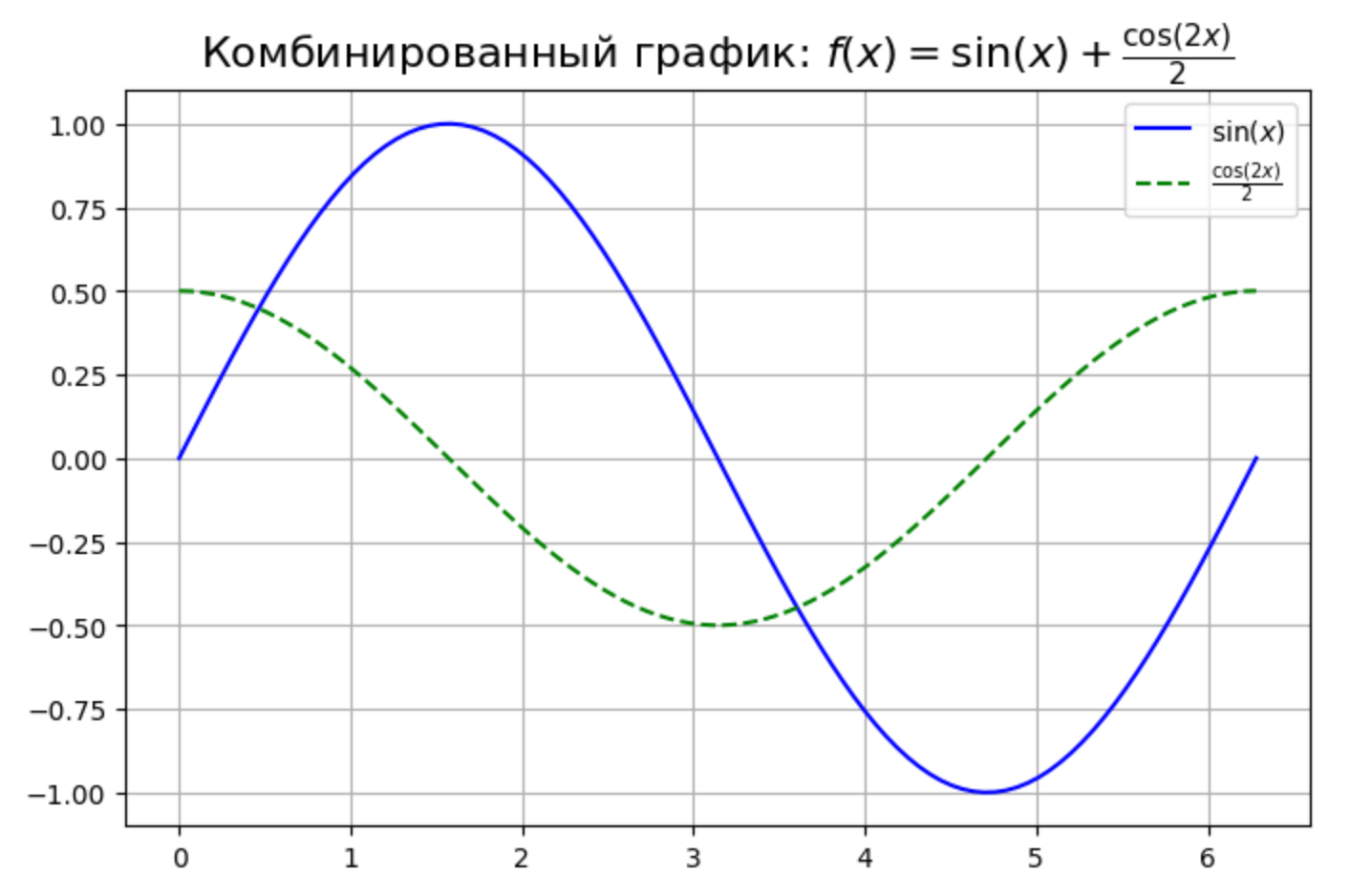
В этом примере:

– Мы создаем данные для двух функций (`sin(x)` и `cos(2x)/2`).

– LaTeX-формулы используются для подписей и заголовка графика.

– Каждая функция имеет свой цвет (синий и зеленый со строчной линией).

– В заголовке графика добавлена более сложная LaTeX-надпись, которая включает в себя сумму (`+`) и дробь (`\frac`).

Эти возможности делают Matplotlib мощным инструментом для визуализации данных в Python, позволяя создавать красочные, информативные и индивидуально настраиваемые графики.

2.4. SciPy

`SciPy` – это библиотека для выполнения научных и инженерных расчётов в языке программирования Python. Она предоставляет множество функций для решения различных задач, таких как оптимизация, интегрирование, интерполяция, обработка сигналов, статистика и многое другое. В этом разделе мы рассмотрим подробнее различные аспекты библиотеки SciPy.

2.4.1. Оптимизация

`SciPy` является важным инструментом в области оптимизации функций, и его методы находят применение в различных научных и инженерных областях. Методы оптимизации играют решающую роль в решении задач, связанных с поиском минимума или максимума функции, что является ключевым этапом в различных дисциплинах.

В области машинного обучения и статистики, методы оптимизации `SciPy` могут использоваться для настройки параметров моделей, максимизации правдоподобия или минимизации функций потерь. Это важно при обучении моделей, таких как линейная регрессия, метод опорных векторов, нейронные сети и другие.

В инженерии методы оптимизации применяются для решения задач проектирования, оптимизации параметров систем и управления, а также для минимизации энергопотребления в различных технических приложениях. Это помогает инженерам создавать более эффективные и оптимальные решения.

В физических науках и химии методы оптимизации используются для нахождения минимумов энергии в молекулярных системах, моделирования структур и оптимизации параметров физических моделей.

В экономике и финансах оптимизация часто применяется для портфельного управления, оптимизации стратегий торговли и прогнозирования экономических показателей. Методы оптимизации `SciPy` предоставляют инструменты для решения сложных задач в этих областях.

В исследованиях и разработках новых технологий методы оптимизации используются для нахождения оптимальных параметров и условий, что помогает ускорить процессы и повысить эффективность технологических решений.

Таким образом, `SciPy` с его методами оптимизации представляет собой важный инструмент для ученых, инженеров и аналитиков, работающих в различных областях, где требуется нахождение оптимальных решений для сложных математических и технических задач.

Приведем пример оптимизации с использованием `minimize`:

```python

from scipy.optimize import minimize

import numpy as np

# Определим функцию, которую будем оптимизировать

def objective_function(x):

return x**2 + 5*np.sin(x)

# Начальное предположение

initial_guess = 0

# Вызов функции оптимизации

result = minimize(objective_function, initial_guess)

# Вывод результатов

print("Минимум найден в точке:", result.x)

print("Значение функции в минимуме:", result.fun)

```

Результат:

Минимум найден в точке: [-1.11051052]

Значение функции в минимуме: -3.2463942726915387

2.4.2. Интегрирование

`SciPy` предоставляет мощные инструменты для численного интегрирования функций, что находит широкое применение в различных областях науки и техники. Одним из ключевых применений является решение математических задач, в которых необходимо вычисление определенных интегралов. Например, в физике для вычисления площади под кривой в графиках функций, в эконометрике для вычисления интегралов в статистических моделях, а также в многих других областях.

В области физики `SciPy` может использоваться для вычисления интегралов, представляющих физические величины, такие как плотность энергии, массы или электрического заряда. Это обеспечивает ученым и инженерам возможность решать сложные математические задачи, связанные с физическими явлениями.

В математической статистике и эконометрике численное интегрирование может быть применено для оценки параметров статистических моделей, а также для вычисления вероятностей и плотностей распределений. Это важный шаг при анализе данных и построении статистических выводов.

В инженерных расчетах `SciPy` может использоваться для решения интегральных уравнений, которые описывают различные физические процессы или связи между переменными в системах. Это позволяет инженерам проводить анализ и оптимизацию проектов, учитывая сложные математические зависимости.

Все эти примеры подчеркивают важность численного интегрирования функций в `SciPy` для решения различных задач в науке, технике и прикладной математике.

Например, `quad` может использоваться для вычисления определенного интеграла:

```python

from scipy.integrate import quad

import numpy as np

# Определим функцию для интегрирования

def integrand(x):

return x**2

# Вызов функции интегрирования

result, error = quad(integrand, 0, 1)

# Вывод результатов

print("Результат интегрирования:", result)

print("Погрешность:", error)

```

Результат:

Результат интегрирования: 0.33333333333333337

Погрешность: 3.700743415417189e-15

2.4.3. Интерполяция

`SciPy` предоставляет мощные инструменты для интерполяции данных, что находит применение в различных областях науки и техники. В научных исследованиях интерполяция используется для восстановления значений между экспериментальными точками данных, что является неотъемлемым этапом в анализе и обработке данных. Этот инструмент также находит применение в геофизике и картографии, где необходимо создавать более плавные картографические изображения или модели на основе неравномерно распределенных данных.

В области медицинской обработки изображений `SciPy` позволяет проводить интерполяцию значений пикселей внутри изображений, что полезно при увеличении разрешения изображений или восстановлении деталей. В компьютерном зрении, где необходимо точно определять объекты на изображении, интерполяция может быть важным инструментом для анализа и обработки изображений.

В финансовых исследованиях, особенно при анализе цен акций с нерегулярными данными, интерполяция помогает строить более гладкие кривые для анализа и моделирования временных рядов. В инженерных приложениях интерполяция может использоваться для восстановления промежуточных значений в экспериментах или для создания более точных геометрических моделей. Все эти применения подчеркивают важность методов интерполяции данных, предоставляемых `SciPy`, в различных областях исследований и промышленности.

Например, `interp1d` может использоваться для создания интерполяционной функции:

```python

from scipy.interpolate import interp1d

import numpy as np

import matplotlib.pyplot as plt

# Исходные данные

x = np.array([1, 2, 3, 4, 5])

y = np.array([2, 0, 1, 3, 7])

# Создание интерполяционной функции

f = interp1d(x, y, kind='cubic')

# Создание более плотного набора точек для отображения интерполяции

x_new = np.linspace(1, 5, 100)

y_new = f(x_new)

# Визуализация результатов

plt.scatter(x, y, label='Исходные данные')

plt.plot(x_new, y_new, label='Интерполяция (кубическая)')

plt.legend()

plt.show()

```

В библиотеке `SciPy` есть множество модулей, предоставляющих различные функциональности для научных и инженерных вычислений. Вот несколько других модулей, которые могут быть полезными:

2.4.4. `scipy.signal` (Обработка сигналов)

Модуль `scipy.signal` в библиотеке SciPy предоставляет обширные инструменты для обработки сигналов, что делает его полезным в различных областях науки и техники. Одной из основных областей применения является телекоммуникация и обработка сигналов, где он используется для фильтрации и улучшения качества сигналов, а также для анализа частотных компонентов при помощи преобразования Фурье.

В области медицинской техники модуль применяется для анализа биомедицинских сигналов, таких как ЭКГ и ЭЭГ, что помогает в диагностике и мониторинге здоровья пациентов. В звуковой обработке и музыкальной индустрии он используется для улучшения качества аудиосигналов и анализа музыкальных характеристик.

Для работы с изображениями модуль применяется в области обработки изображений и компьютерного зрения. Он позволяет фильтровать и улучшать контрастность изображений, а также выполнять анализ и выделение объектов на изображениях. В контроле и автоматике он используется для анализа сигналов в системах управления и фильтрации для устойчивости систем.

В электронике и схемотехнике модуль `scipy.signal` применяется для фильтрации сигналов в электронных устройствах и проектирования аналоговых и цифровых фильтров. Эти функции делают его важным инструментом для инженеров, занимающихся разработкой и анализом электронных систем. Модуль предоставляет функции, такие как `convolve` для свертки и `spectrogram` для создания спектрограммы, делая его мощным средством обработки сигналов в различных областях.

```python

from scipy import signal

# Пример: Проектирование фильтра

b, a = signal.butter(4, 0.1, 'low')

```

2.4.5. `scipy.stats` (Статистика)

Модуль `scipy.stats` в библиотеке SciPy предоставляет обширный функционал для работы со статистическими распределениями, тестированиями гипотез и другими операциями, связанными со статистикой. Этот модуль находит применение в различных областях научных исследований, где требуется анализ данных с точки зрения статистики.

В научных исследованиях модуль используется для проведения статистических тестов, таких как t-тесты или анализ дисперсии (ANOVA), что позволяет исследователям делать выводы на основе статистической значимости данных. В медицинской статистике этот модуль применяется для анализа эффективности лекарств и клинических испытаний, оценки влияния различных факторов на здоровье пациентов.

Экономисты исследуют экономические данные с использованием статистических методов для анализа тенденций, прогнозирования и определения влияния различных факторов на экономику. В социальных науках модуль помогает анализировать данные об общественном мнении, социальных явлениях и взаимосвязях в обществе.

В инженерных исследованиях статистика применяется для анализа результатов экспериментов, проверки надежности и статистического проектирования. В области финансов, статистический анализ применяется для оценки рисков, анализа рынков и стратегического планирования в инвестиционных портфелях.

Модуль `scipy.stats` также находит свое применение в образовательных исследованиях, где он используется для анализа результатов экзаменов, эффективности образовательных программ и оценки образовательных процессов. В биоинформатике, этот модуль может применяться для анализа геномных данных и выявления статистически значимых различий в экспрессии генов. Обширный функционал `scipy.stats` делает его важным инструментом для исследователей и аналитиков, работающих в областях, где требуется статистический анализ данных.

```python

from scipy import stats

# Пример: Генерация выборки из нормального распределения

data = stats.norm.rvs(size=1000)

```

2.4.6. `scipy.linalg` (Линейная алгебра)

Модуль `scipy.linalg` является неотъемлемой частью библиотеки SciPy и предоставляет богатый набор функций для решения задач линейной алгебры. Этот модуль находит применение в различных научных и инженерных областях, где операции с матрицами и линейные уравнения играют важную роль.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Конец ознакомительного фрагмента

Купить и скачать всю книгу

<1 2 3

На страницу:

Перейти

3 из 3