Математические игры с дурацкими рисунками: 75¼ простых, но требующих сообразительности игр, в которые можно играть где угодно

Я не смогу изложить исчерпывающую теорию «Точек-клеточек» в одной короткой главе. Однако вас ждет кое-что получше: полное математическое исследование из первых рук, от ученого, который первым опубликовал правила этой игры.

Станете ли вы после прочтения этой главы популярным, сложным и насыщенным математикой ребенком? Трудно сказать. Так что просто читайте и двигайтесь дальше.

КАК ИГРАТЬ

Сколько игроков? Двое.

Что потребуется? Два карандаша разных цветов и поле с рядами точек. Рекомендую поле 6 × 6 точек, но в принципе подойдет любое прямоугольное поле.

В чем цель? Начертить больше квадратов, чем противник.

Какие правила?

1. Поочередно соединяйте соседние точки вертикальными или горизонтальными линиями.

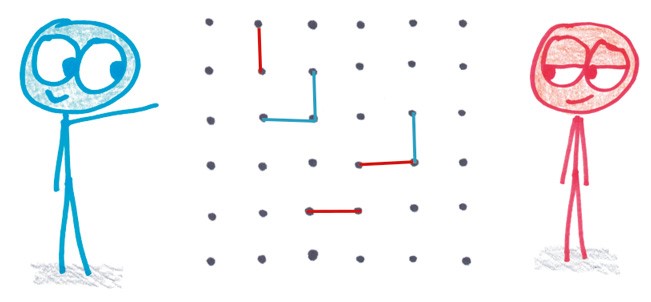
2. Тот, кто дочертит квадрат, набирает одно очко, помечает этот квадрат (например, своими инициалами) и делает следующий ход.

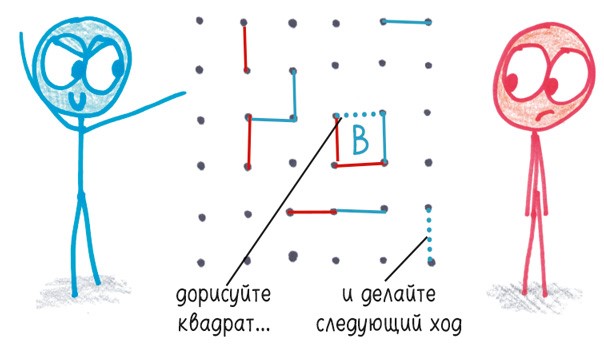
Это правило позволяет вам дочертить целую вереницу квадратов, прежде чем противник дождется своего хода.

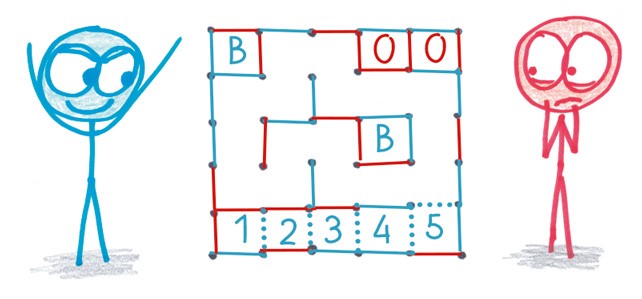
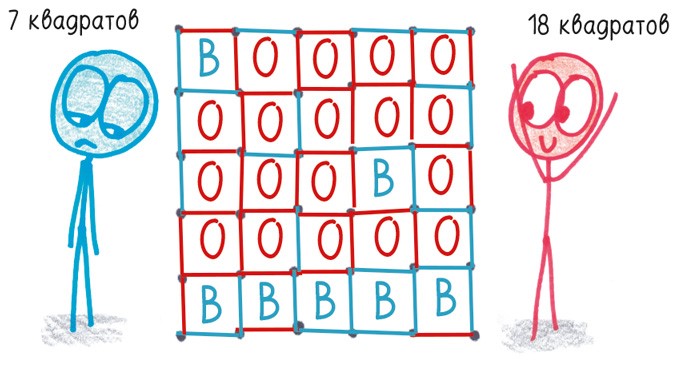
3. Играйте, пока не соедините все точки. Кто наберет больше очков, тот и победил.

ЗАМЕТКИ ДЕГУСТАТОРА

Впервые я сыграл в эту игру в детстве, в подвале с полками, набитыми видеокассетами, под аккомпанемент тяжелой поступи динозавров. Нам с братьями не хватало стратегического мышления: в основном мы действовали наобум, стараясь просто не рисовать третью сторону квадратов (чтобы противник не нарисовал четвертую) и волей-неволей рассредоточивали свои линии[7]. Рано или поздно безопасных ходов не оставалось. Тогда-то и наступала самая напряженная стадия игры.

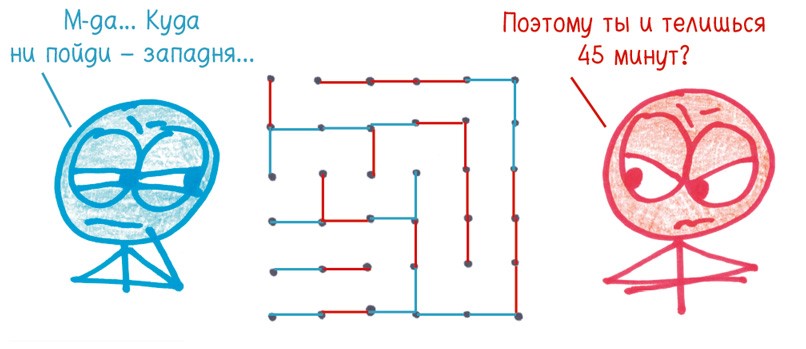
Теперь жертвы становились неизбежными, хотя и не все были равноценными. Некоторые ходы позволяли противнику набрать лишь одно или два очка, а другие – заполонить своими квадратами практически все поле. Я всегда старался жертвовать самыми маленькими областями, надеясь отвоевать те, что покрупнее.

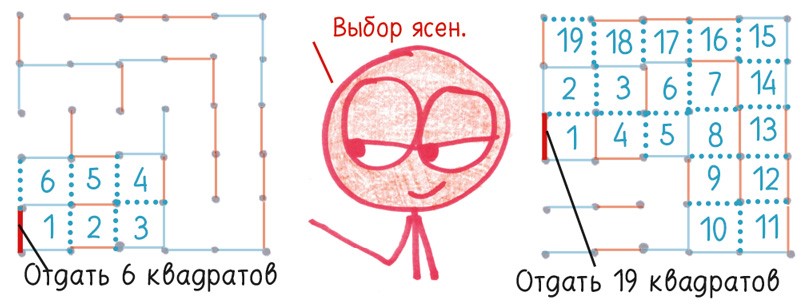
Годы спустя, работая над этой книгой, я освоил важную стратегию, незамысловатую, но позволяющую обыгрывать 99 % новичков: двойной крест. Идея в том, что вы ломаете противнику весь кайф, когда он уже нацелился сделать триумфальный ход. Просто сократите свой ход, не начертив предпоследнюю линию. Таким образом, рисуя одну линию, вы жертвуете двумя квадратами, которые получит ваш противник (поэтому крест двойной). В обмен вы завладеете всей областью, на которую положил глаз ваш оппонент.

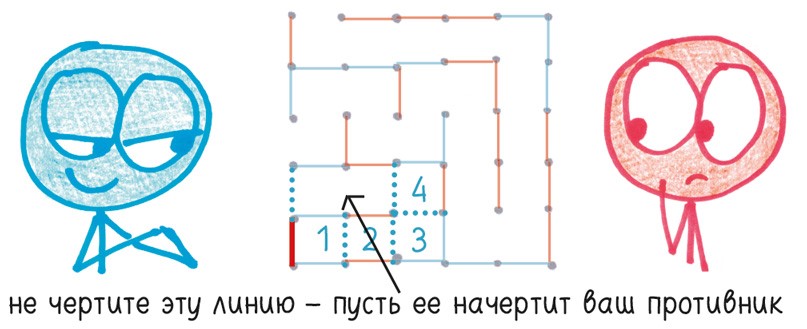
За пределами этой стратегии всё становится сложным и неясным. Детали вы можете почерпнуть из трудов великого Элвина Берлекампа. Он скончался, когда я работал над этой книгой, и навсегда останется в нашей памяти как ненасытное дитя математической сложности.

ГЕНЕАЛОГИЯ ИГРЫ

Сегодня в «Точки-клеточки» играют практически везде: на черных, белых и зеленых школьных досках, в желтых блокнотах юристов, на ресторанных салфетках или за неимением лучшего на собственных ладонях[8]. Впервые правила игры опубликовал математик Эдуард Люка в 1889 году. Он называл ее Pipopipette. По словам Эдуарда, игру придумали его бывшие студенты из престижной парижской Политехнической школы.

Странно, не правда ли? Зачем серьезным студентам тратить время на придумывание детской игры? И почему такой уважаемый ученый решил опубликовать статью о ней?

Ответ прост: потому что серьезная математика часто рождается именно из детских игр.

Мы видим эту закономерность даже в карьере Эдуарда. Пожалуй, он наиболее известен своим исследованием последовательностей наподобие чисел Фибоначчи, где каждое следующее число – сумма двух предыдущих. (Классическая последовательность: 1, 1, 2, 3, 5, 8 и так далее.) Числа Фибоначчи кажутся глупой забавой до тех пор, пока вы не начнете подсчитывать лепестки маргаритки, семена подсолнуха или ананаса. Тогда вы убедитесь, что в эту глупую игру играют не только дети (и неповзрослевшие взрослые), но и сама природа.

Вот еще одна любимая задача Эдуарда: головоломка с пушечными ядрами. Суть в том, чтобы найти число пушечных ядер, из которых можно сложить идеальный квадрат и идеальную пирамиду. Задача выглядит пустяшной. Однако она дьявольски сложна. Эдуард предположил, что известное решение (4900 пушечных ядер) – единственное.

Десятилетия спустя исследование эллиптических функций доказало его правоту.

Но самое знаменитое изобретение Эдуарда – «Ханойская башня». Наверняка вы видели такие игрушки. Башня состоит из трех стержней и набора дисков разного диаметра, образующих пирамиду. Цель состоит в том, чтобы перенести пирамиду с одного стержня на другой, перемещая по одному диску за раз и никогда не укладывая больший диск поверх меньшего.

На первый взгляд башня, как бы это сказать помягче, детская забава. Тем не менее у нее множество практических применений. Психологи используют ее для проверки когнитивных способностей; преподаватели информатики – для обучения рекурсивным алгоритмам; инженеры-программисты – в качестве схемы ротации при резервном копировании данных.

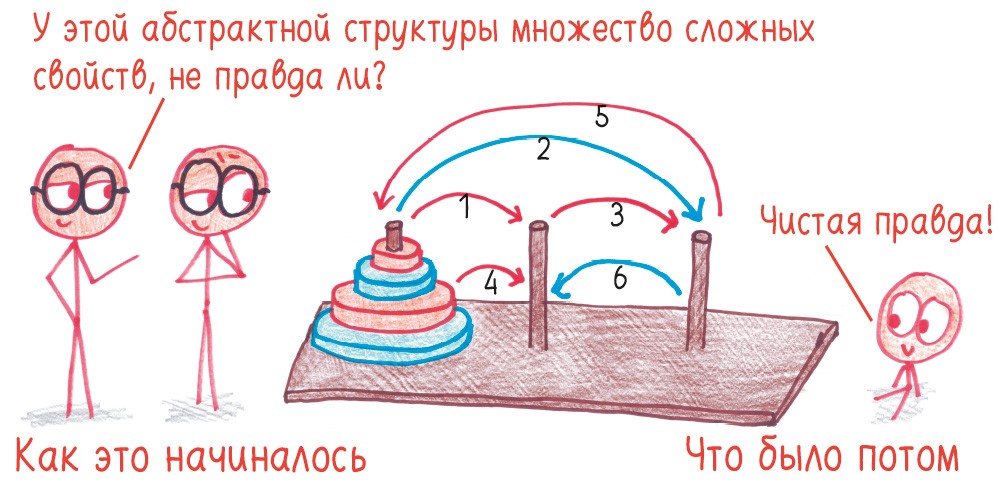
Почему праздное времяпрепровождение с легкостью превращается в научное исследование? Почему граница между работой и досугом такая зыбкая и проницаемая?

Честно говоря, не знаю. Подозреваю, Эдуард тоже не знал. Можно сказать лишь одно: простые математические предпосылки приводят к глубоким выводам. Вот что такое математика на самом деле: сложное взаимодействие простых идей. Эдуард так говорил о «Точках-клеточках»: «Несмотря на всю свою незамысловатость, на практике эта игра преподносит сюрприз за сюрпризом».

ПОЧЕМУ ЭТА ИГРА ВАЖНА?

Потому что бесполезная игра часто рождает наиполезнейшие идеи.

В первой публикации, посвященной «Точкам-клеточкам», Эдуард Люка пространно рассуждает о ценности чистого любопытства. Он приводит множество исторических примеров и утверждает, что мы должны задавать вопросы спонтанно, какими бы глупыми они ни казались, поскольку неизвестно, насколько глубокие истины можно раскрыть.

Его стиль довольно витиеватый, однако все равно я процитирую[9]:

Каждый математик хочет вскрыть глубокие связи между несопоставимыми идеями. Вопрос в том, как этого добиться. Напряженно работать? Возможно. Терпеливо вычислять? Не повредит. Подсмотреть ответ в конце задачника? Простите, не угадали. Позволить воображению резвиться?

А вот здесь есть о чем поговорить.

Эдуард верил, что глубина возникает из игры, наука – из дуракаваляния. И он был не одинок. Элвин Берлекамп научился играть в «Точки-клеточки», когда ему было 6 лет, и спустя 70 лет все еще не утратил интереса к ним. Он играл на протяжении всей жизни. И где-то посредине странствия земного, когда он изучал электротехнику в Массачусетском технологическом институте, его осенило: можно использовать математику, чтобы создать «дуальную игру», которую он окрестил «Нити и монеты».

Как выглядит эта альтернативная версия? Нарисуйте монеты, соединенные нитями. Один конец каждой нити приклеен к какой-либо монете, а другой – либо к соседней монете, либо к столу. Игроки поочередно разрезают нити ножницами. Если монета высвобождается, она достается вам, и вы зарабатываете право на еще один ход. Игра длится до тех пор, пока игроки не разберут все монеты. Побеждает тот, у кого больше монет.

Никаких квадратиков – лишь монеты. Никаких отрезков – лишь натянутые нити. Но, по сути, игра та же самая. Не меняя принципиальную структуру, Элвин вывернул «Точки-клеточки» наизнанку.

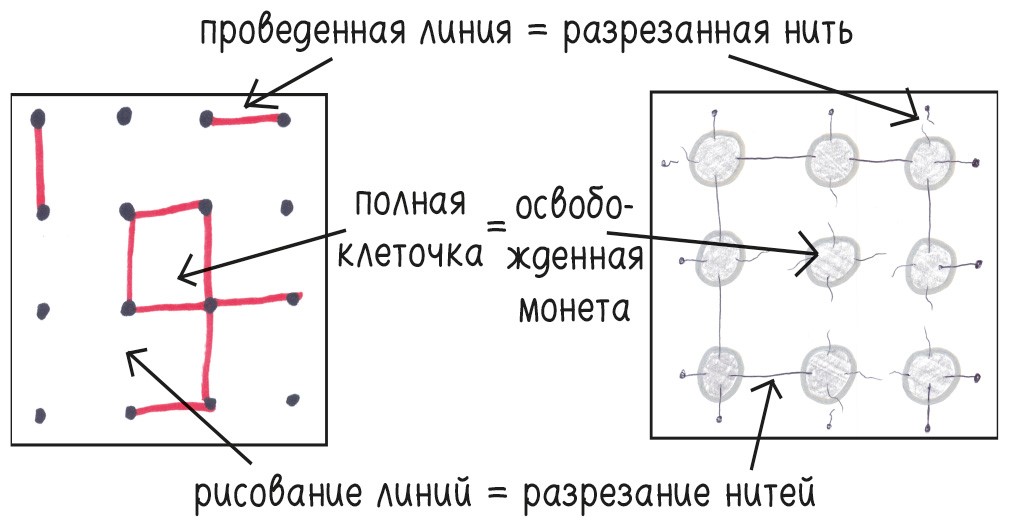
Зачем? Да просто так. Забавы ради. «Пусть мыслители мыслят, а мечтатели мечтают, – писал Эдуард Люка, – не тревожась о том, что иногда занимаются чем-то несерьезным или бесполезным, ибо, по словам мудреца Анаксагора, во всём есть часть всего».

Эта философия вдохновляла математические изыскания на протяжении тысячелетий, и она прослужит нам еще тысячелетия. Пусть мыслители мыслят. Пусть мечтатели мечтают. Пусть студенты чертят закорючки на полях конспектов лекций. Не проводите границу между практичным и непрактичным, полезным и бесполезным, пустым и идеальным. Это области одного и того же необитаемого континента, одной и той же прекрасной девственной земли, которую мы лишь начали изучать.

ВАРИАЦИИ И РОДСТВЕННЫЕ ИГРЫ

Шведская доска. Границы поля уже нарисованы.

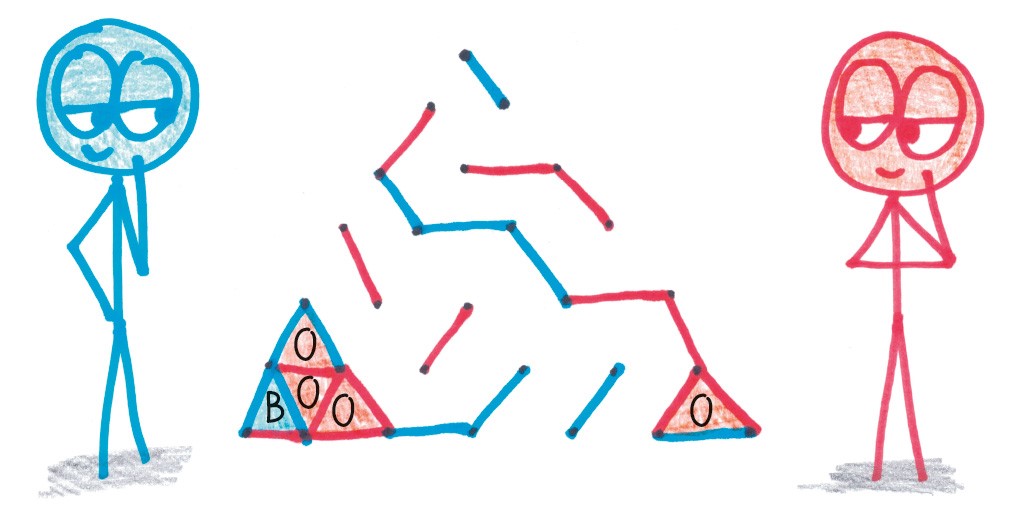
Точки-треугольнички. Правила те же, но вы играете на треугольном поле и сражаетесь за равносторонние треугольники. На мой взгляд, это делает игру красивее (к тому же треугольники легче начертить). Идеальное решение, если вас утомил классический вариант игры, а курьер с пиццей еще не прибыл.

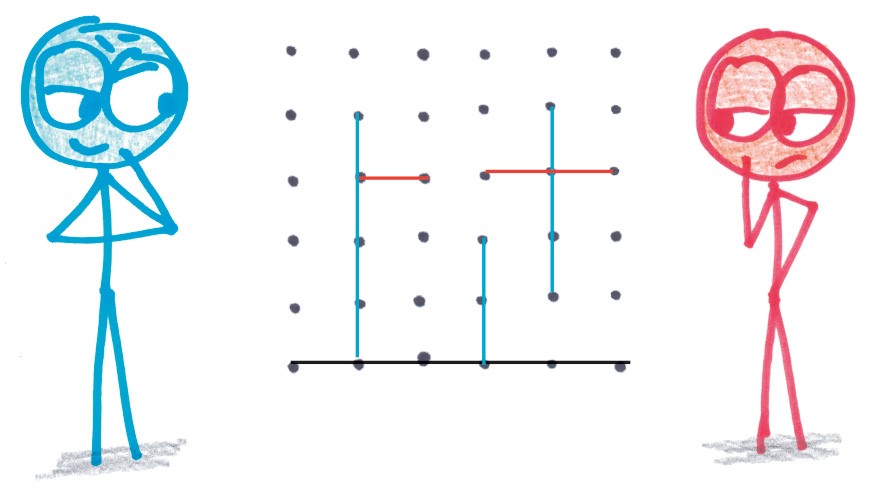
Назарено. В этом усовершенствованном варианте игры из книги Андреа Анджолино «Отточенный карандаш и игры на бумаге» меняются два правила. Во-первых, вы можете проводить прямую линию любой длины, если она не пересекает уже начерченные линии. (Таким образом, вы можете дорисовать несколько квадратов сразу.) Во-вторых, если вы дорисовали квадрат, то не получаете дополнительный ход.

Если новое правило в «Точках-треугольничках» меняет вид знакомой игры, то в «Назарено» все наоборот: в знакомой игре открываются новые горизонты.

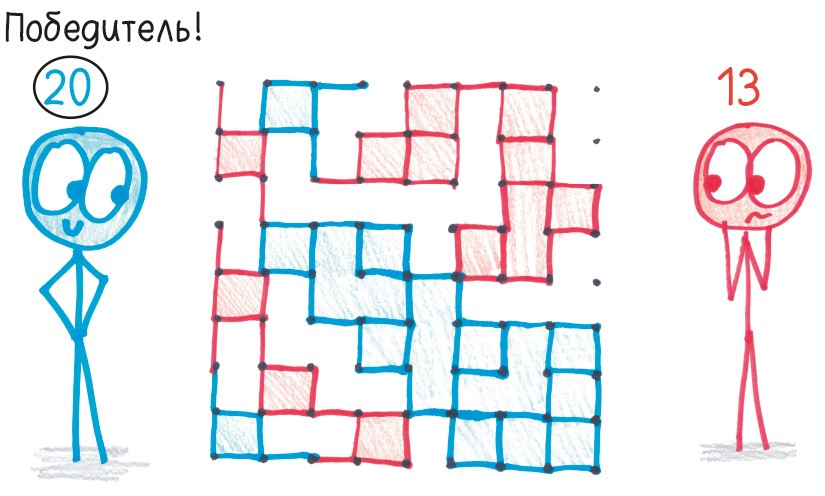
Квадратный полип. Свихнувшийся визионер Уолтер Джорис в книге «Сто стратегических игр с карандашом и бумагой» предлагает несколько игр, напоминающих «Точки-клеточки». Моя любимая – 90-я по счету: «Квадратный полип». Участвуют два игрока. Понадобятся цветные карандаши.

1. Нарисуйте поле 9 × 9 точек (или поменьше, если вы новичок; или побольше, если вы знаток) и по очереди рисуйте квадратные полипы. Это квадраты с двумя ответвлениями, например:

2. Стремитесь захватить как можно больше квадратов. Каждый полип автоматически занимает квадрат 1 × 1, но умелый игрок может получить области покрупнее и более причудливой формы.

3. Линии не должны пересекаться[10]. Это правило позволяет сорвать планы противника, выпустив одно-единственное смертоносное щупальце (но будьте осторожны: противник может настолько же легко сорвать ваши планы).

4. Играйте до тех пор, пока не останется ни одного хода. Выигрывает тот, кто занял наибольшую часть поля.

Ростки

ИГРА С «ЛЮБОПЫТНЫМ ТОПОЛОГИЧЕСКИМ КОЛОРИТОМ»

Из школьной геометрии мы выносим одну пренеприятную истину: размер имеет значение. И в самом деле, размер – одно из основополагающих свойств в материальном мире. Углы бывают острыми, прямыми или тупыми. Фигуры имеют длину, площадь или объем. Порция мокко с соленой карамелью может быть большой, маленькой или средней. Так или иначе все сводится к размеру. Черт возьми, само название школьного предмета недвусмысленно об этом говорит: в переводе с древнегреческого оно означает «землемерие».

Вас раздражает такая зацикленная на размере философия? Тогда вам понравится топология. Там фигуры растягиваются, словно резина, податливы, словно пластилин, раздуваются, словно воздушные шары. Не фигуры, а трансформеры! В этом текучем мире лавовых ламп размер не имеет значения. По сути, о размерах там не идет и речи.

Топология ищет более глубокие истины.

Хотите узнать какие? Для первого знакомства лучше всего подойдет игра «Ростки». Какие точки можно соединить? Сколько областей возникнет? В чем разница между «внутри» и «снаружи»? Придержите свои шляпы – или их топологические эквиваленты – и наслаждайтесь игрой, правила которой легко поймет любой ребенок, но перебрать варианты развития событий не под силу ни одному суперкомпьютеру.

КАК ИГРАТЬ

Сколько игроков? Двое (или больше).

Что потребуется? Разноцветные карандаши и бумага. Вначале нарисуйте несколько точек. На первое время ограничьтесь тремя-четырьмя.

В чем цель? Побеждает тот, кто сделает последний ход в игре, не оставив противнику ни одного варианта.

Какие правила?

1. Во время каждого хода рисуйте одну линию (прямую или кривую), соединяющую две точки либо возвращающуюся к исходной точке, и ставьте новую точку где-нибудь на этой линии.

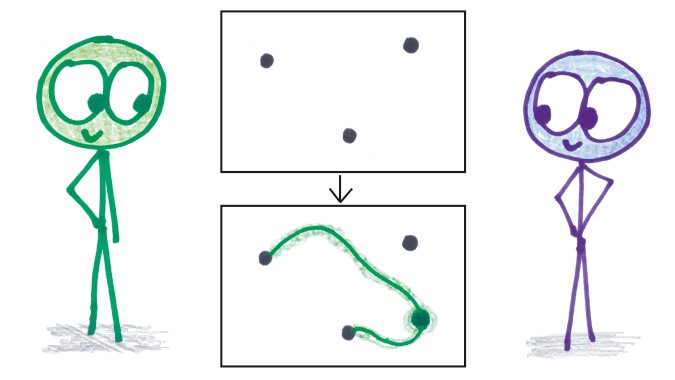
2. Всего два ограничения: (1) линии не могут пересекать себя или друг друга; (2) из каждой точки может исходить не более трех линий.

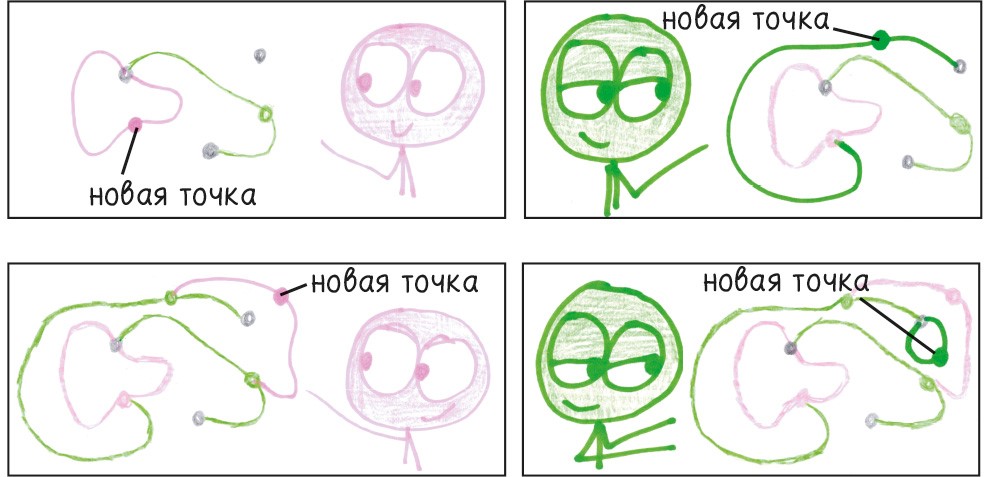
3. В конце концов все возможности будут исчерпаны. Выигрывает тот, кто сделает последний ход.

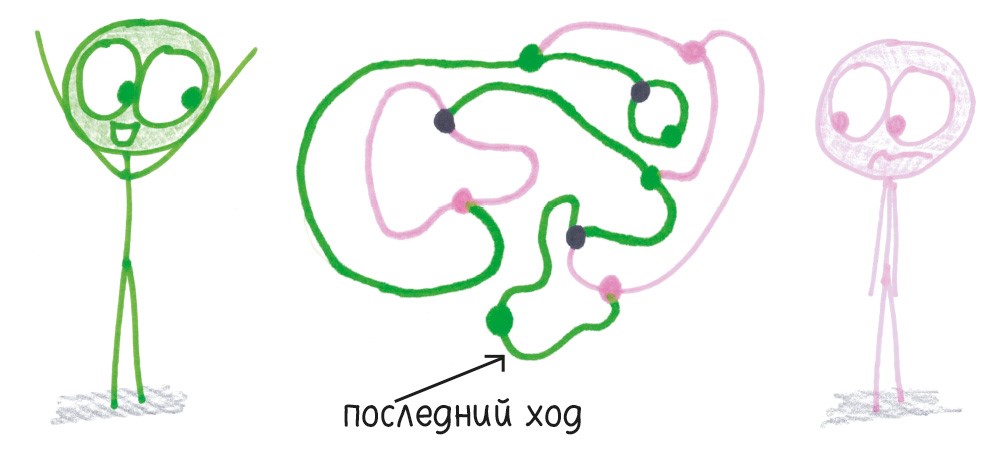
ЗАМЕТКИ ДЕГУСТАТОРА

Прелесть «Ростков» в гибкости линий. Неважно, какие они: прямые, плавные кривые или витиеватые спирали; значение имеют только соединяемые точки. Можете даже изобразить свою подпись. Шестиклассница Анджела так и поступила, когда мы попробовали сыграть, и, хотя в принципе она нарушила правило (линии самопересекались), это настолько впечатляло, что я не возражал.

Такая гибкость отражает суть топологии: вещи могут быть совершенно непохожими друг на друга, но иметь одинаковый функционал.

Рассмотрим вариант, где вначале на игровом поле всего одна точка. Первый игрок волей-неволей рисует петлю и ставит новую точку на ней. Второй игрок должен соединить две точки. Кажется, возможны два варианта: нарисовать линию внутри петли или снаружи.

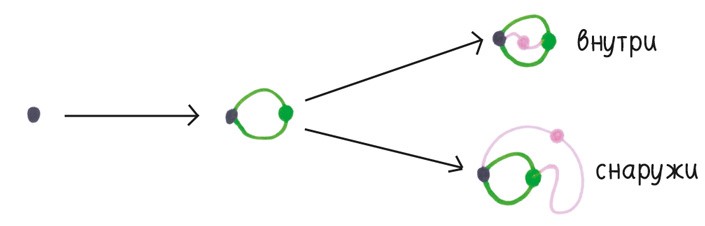
Но погодите-ка. Представьте, что вы чертите линии на сфере. Особо ничего не меняется, но теперь неважно, рисуете ли вы вторую линию «внутри» или «снаружи». С точки зрения топологии эти два хода идентичны. Таким образом, в действительности у второго игрока нет выбора.

А как насчет игры, которая начинается с двух точек? У первого игрока есть лишь два варианта: соединить эти две точки или нарисовать петлю. Неважно, будет ли вторая точка «внутри» или «снаружи» петли. Топологически нет разницы.

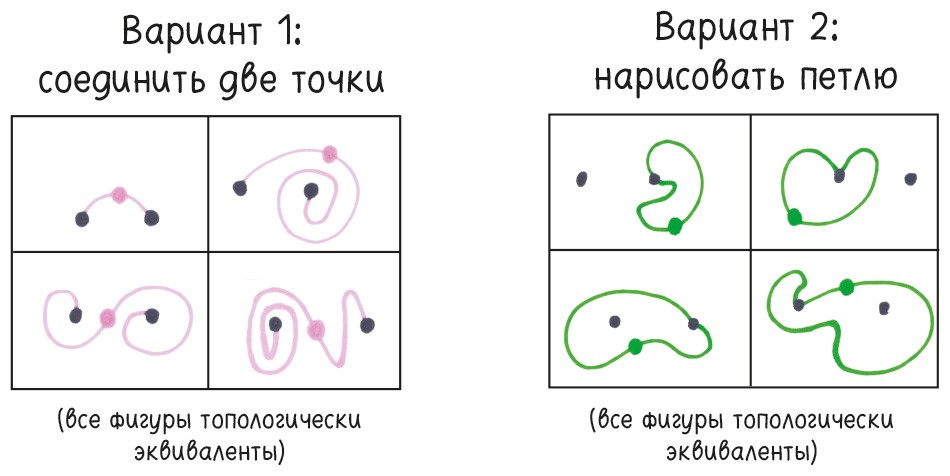
Неужели топологи не замечают различий и все вещи для них на одно лицо? «Победа» топологически равноценна «поражению»? «Хорошо» топологически то же самое, что «плохо»? Кошка топологически эквивалентна рыбке и в аквариум нужно поставить маленький кошачий лоток?

Решайте сами, если у вас есть домашние питомцы. Но, играя в «Ростки», не стоит беспокоиться. Не все ходы эквивалентны. По сути дела, когда все начинается с двух точек, уже ко второму ходу возникает шесть топологически разных вариантов. Свободы становится все больше.

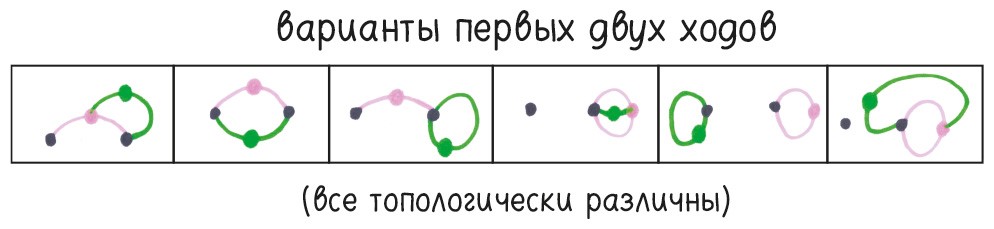
В «Точках-клеточках» мы имели дело с жесткой, прямолинейной геометрией, подобной градостроительному плану. «Ростки», напротив, свободолюбивая игра, похожая на хаос карнавального шествия.

ГЕНЕАЛОГИЯ ИГРЫ

Место и время рождения «Ростков» точно известны: Великобритания, Кембридж, вторая половина дня во вторник 21 февраля 1967 года.

Родители игры, кибернетик Майк Патерсон и математик Джон Конвей, рисовали закорючки на листе бумаги, пытаясь изобрести новую игру. Майк предложил правило с добавлением новой точки, Джон предложил название. Так родились «Ростки»[11]. Они поделили честь открытия в соотношении 60/40 в пользу Майка: эта честная и точная пропорция впечатляет не меньше, чем само рождение игры.

В «Ростки» просто играть, но сложно перебрать все варианты. Анализ игры, начинающейся с шести точек, занял у Дениса Моллисона 47 страниц. Никто не превысил эту планку до 1990 года, когда компьютер Bell Labs перебрал все варианты игры, начинающейся с 11 точек. На момент написания этой главы перебраны все варианты для игры, начинающейся с 40 точек, хотя Конвей перед кончиной в 2020 году скептически высказался на сей счет: «Вы поверите, услышав, что кто-то изобрел машину, которая может сочинить пьесу, достойную пера Шекспира? Это слишком сложно».

Отпугнула ли эта сложность игроков-любителей? Ничуть.

«На следующий день после того, как проросли "Ростки", – пишет Конвей, – в них стали играть все подряд. За чаем и кофе небольшие компании не могли взгляда оторвать от нелепых или фантастических вариантов развития игры… Общему поветрию поддались и секретари… Рисунки с "Ростками" можно было обнаружить в самых неожиданных местах… Даже мои дочки, которым три и четыре года, играли в них, хотя обычно я выигрывал».

ПОЧЕМУ ЭТА ИГРА ВАЖНА?

Потому что среди разделов современной математики топология – одна из наиболее (1) динамичных, (2) причудливых, (3) полезных и (4) красивых.

Эпитетов много, так что разберем их по порядку.

Топология динамична. Топологи живут в изменчивом мире растягивающейся резины, расплавленного металла и тающего мороженого. Они постоянно ищут инварианты: свойства, которые остаются неизменными, несмотря на все перипетии.

Наиболее известный инвариант – эйлерова характеристика. Для «Ростков» все сводится к простому уравнению (это заметил Эрик Соломон): точки + области = линии + фигуры.

Это уравнение верно на любом этапе игры для всех возможных сценариев, от простейшего до сложнейшего, независимо от того, начинаете ли вы с двух точек или с двух миллионов. В любой ситуации количество точек плюс количество замкнутых областей будет равно количеству линий, соединяющих точки, плюс количество отдельных фигур[12].

Это типично для топологии: в необузданно меняющемся мире мы находим стройные закономерности.

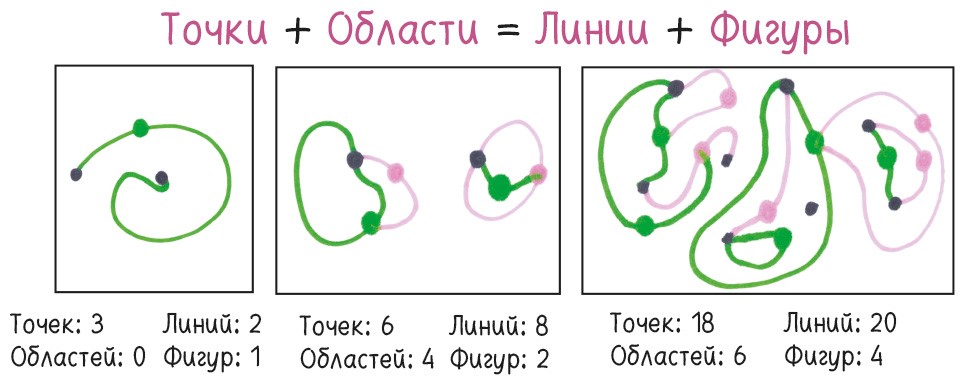
Топология причудлива. Вот забавное открытие Джона Конвея. Если количество ходов минимально, то в конце концов вы получите (грубо говоря) одну из этих фигур:

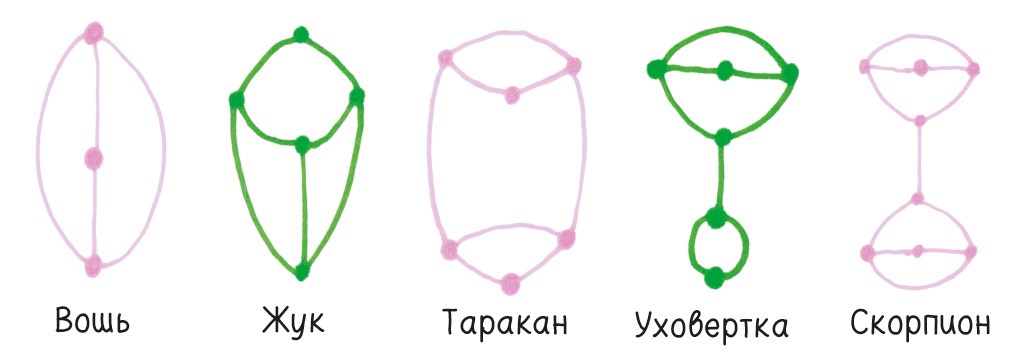
В классическом пособии «Выигрышные стратегии математических игр» объясняется, что окончательная конфигурация «будет представлять собой одно из этих насекомых (возможно, вывернутое наизнанку), к которому присосалось произвольное количество вшей (к некоторым вшам могут присосаться другие)».

В общем, вшей довольно много. Причем одни конфигурации, по замечанию Конвея, «вшивее» других.

Топология полезна. Несмотря на балаган с уховертками и вшами, топология помогает разобраться с самыми разными вещами, от запутанности ДНК до запутанности социальных сетей, не говоря уже о космологии и квантовой теории поля.

Рассмотрим знаменитую топологическую проблему: изоморфизм графов. Мы уже знаем, что две конфигурации в «Ростках» могут выглядеть по-разному, но быть структурно одинаковыми. Как определить, различаются ли две сети или они идентичны, хотя на первый взгляд непохожи?

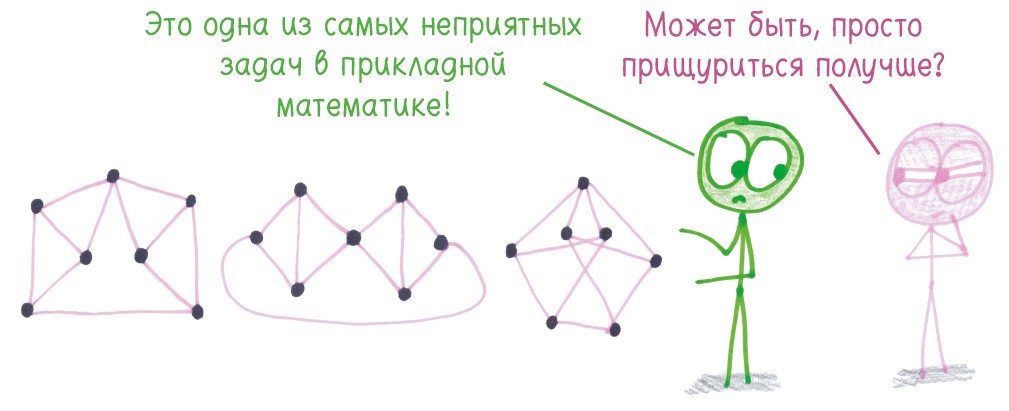
Этот вопрос тревожит инженеров, сопоставляющих электрические схемы, компьютерщиков, кодирующих визуальную информацию, и химиков, ищущих соединения в базах данных. По сути дела, все эти серьезные люди играют в свои версии «Ростков».

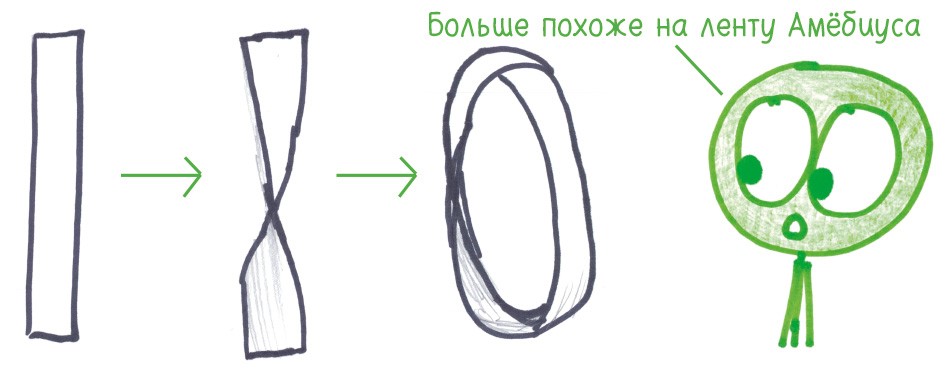
Топология красива. Для многих знакомство с топологией начинается с ленты Мёбиуса. Возьмите полоску бумаги, перекрутите ее и склейте концы.

У ленты Мёбиуса всего одна поверхность: нет дихотомии «внутри» и «снаружи». Если вы решите использовать ее в качестве браслета и попытаетесь покрасить внутреннюю сторону в синий, а внешнюю в красный, ничего не получится. И это лишь одна из странностей. Что будет, если разрезать ленту Мёбиуса вдоль? А если попытаться разрезать ее на три части?

Математик Дэвид Ричесон в книге «Жемчужина Эйлера» подсчитал, сколько медалей Филдса (самая престижная награда в области математики) досталось топологам. «Из 48 лауреатов, – пишет он, – примерно треть были награждены за работы в области топологии, и еще больше – за вклад в тесно связанные с ней области».

Если красота – дочь сложности и простоты, то «Ростки» – настоящее дитя любви.

ВАРИАЦИИ И РОДСТВЕННЫЕ ИГРЫ

Сорняки. Автор – Владимир Игнатович. Игроки могут рисовать на своей линии одну точку, две или ни одной.

Набери очки. Автор – Уолтер Джорис. Правила те же, что в «Ростках», но ведется подсчет очков. Если в результате вашего хода образуется замкнутая область, пометьте ее инициалами или цветом и подсчитайте количество точек на границе области (одна точка – одно очко). Рисовать новые линии внутри этой области запрещено. Когда все ходы будут исчерпаны, побеждает тот, у кого больше очков[13].

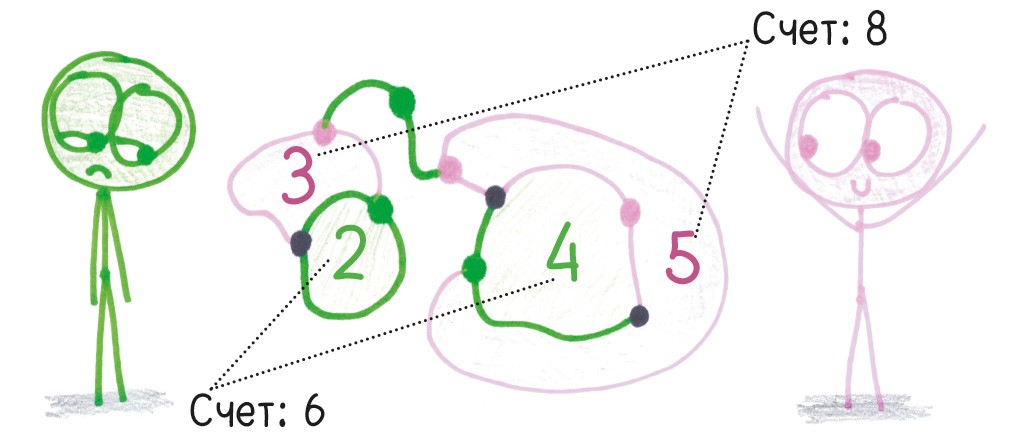
Брюссельская капуста. Эта скверная сестра-близнец «Ростков» на первый взгляд кажется такой же многовариантной и требующей стратегического мышления. Но это не так. Скорее это не игра, а какая-то пародия.

Вначале нарисуйте несколько крестиков. Соединяйте любые два свободных конца и ставьте черточку на новой линии, чтобы получилось еще два свободных конца. Линии не должны пересекаться. Выигрывает тот, кто делает последний ход, когда больше ходов не осталось.

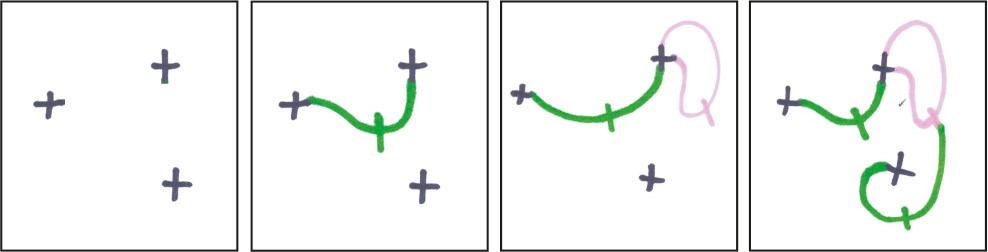
Почему пародия? Дело в том, что исход игры предрешен независимо от действий игроков. Если в начале было нечетное число крестиков, выигрывает первый игрок; если четное – второй. Можете выстраивать какие угодно хитроумные стратегические схемы, всем им грош цена. С тем же успехом можно воображать себя гонщиком «Формулы-1», вращая руль игрушечного автомобиля.

Как это получается? Обратите внимание на то, что количество свободных концов не меняется. Каждый ход уменьшает их на два, а новая черточка добавляет два. Меняется лишь количество областей. После каждого хода, за малым исключением, появляется новая область. В игре с n крестиками на n – 1 ходу нельзя создать ни одну область, соединяя несвязанные крестики.

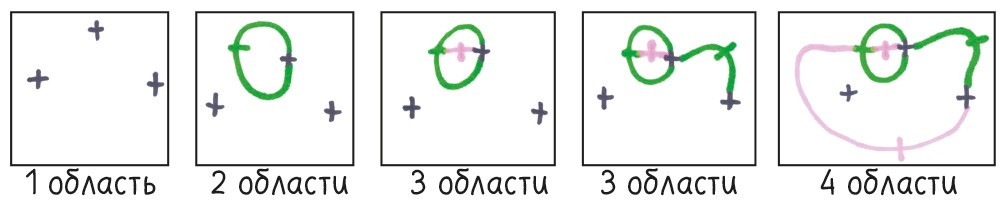
Игра заканчивается, когда количество областей становится равно количеству свободных концов. Для этого требуется 4n – 1 ходов, создающих новые области, плюс n – 1 ход, не увеличивающий количество областей, то есть всего 5n – 2 хода.

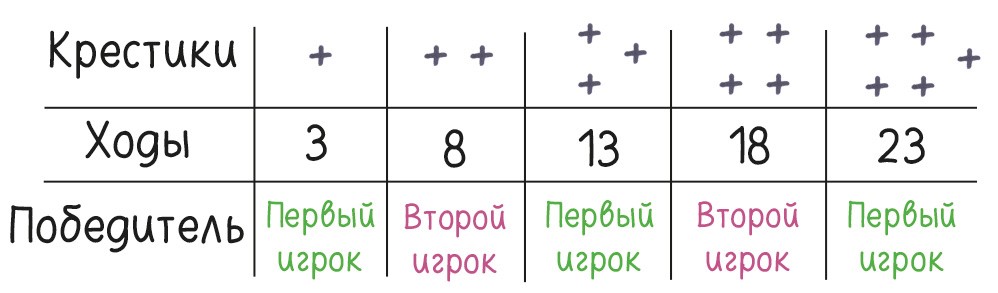
Разыграйте приятеля: предложите сыграть на поле с двумя, четырьмя и шестью крестиками, каждый раз великодушно уступая право первого хода. Когда противник почует подвох и потребует, чтобы вы ходили первым, незаметно переключитесь на игру с тремя или пятью крестиками. Конечно, обманывать нехорошо, особенно друзей… Но пошутить-то можно.

Супер-крестики-нолики

ИГРА С ФРАКТАЛЬНОЙ СТРУКТУРОЙ

В 2013 году, узнав о существовании этой игры на пикнике математиков с нашего факультета, я написал краткий пост в своем блоге. Он вызвал настоящий ажиотаж в интернете, угодив в топ сайта Hacker News[14] и на главную страницу Reddit[15], а кроме того, породил целый букет приложений для смартфонов[16]. Поскольку взлет моей карьеры в немалой мере связан с этой игрой, я много размышлял о том, что делает ее особенной. Элегантность правил? Легкость измышления стратегических идей? Подсознательная ассоциация с «Суперфрисби»?