 полная версия
полная версияNotes and Queries, Number 57, November 30, 1850

Various
Notes and Queries, Number 57, November 30, 1850
NOTES
PORTRAIT OF CARDINAL BEATON
A portrait of this eminent Man was engraved by Pennant, from a picture at Holyrood House, in Part II. of his Tour in Scotland, p. 243. 4to. Lond. 1776. Lodge has an engraving from the same portrait in his collection of Illustrious Personages. This is a strange circumstance; because, when Pinkerton was about to include this portrait in his collection, Pennant wrote to him, on 30th April, 1796, as follows:
"Give me leave to say, that I suspect the authenticity of my Cardinal Beaton. I fear it is Cardinal Falconer or Falconieri. I think there is a genuine one somewhere in Scotland. It will be worth your while to inquire if there be one, and engrave it, and add my suspicions, which induce you do it."—Pinkerton's Correspondence, vol. i. p. 402. 8vo. Lond. 1830.
Pinkerton made inquiry, and on Dec. 1st, 1797, writes to the Earl of Buchan:
"Mr. Pennant informs me the Cardinal Beaton is false. It is, indeed, too modern. A real Beaton is said to exist in Fife."—Pinkerton's Correspondence, vol. ii. p. 17.
Lord Buchan writes to him that Mr. Beaton, of Balfour, believes himself to have a genuine portrait of the Cardinal, and offers it for engraving. The authenticity of this portrait, however, appears not to have been established, and it was not engraved. Another was found at Yester, and was at first concluded to be a genuine original: but Lady Ancram soon discovered that it possessed no marks of originality, but might be a good copy: it was, however, certainly not one of the six cardinals purchased by the third Earl of Lothian. Finally, it was rejected altogether. A copy of a portrait from the Vatican was also rejected as undoubtedly spurious. It appears, therefore, that Pinkerton, in this case at least, exercised caution in the selection of his subject for engraving, so far as concerned authenticity. His criticism, that the Holyrood House portrait is "too modern," will be agreed in by all who will take the trouble to compare the portrait in Lodge with undoubted portraits of the time: the style is too modern by a hundred years. But the portrait is of a man upwards of sixty years old: Beaton was murdered in 1546, in the fiftieth year of his age. The portrait is of a dark haired man without beard.
I now come to a portrait of Beaton which there appears reason to think is genuine, and I beg the favour of your correspondents to give me any information in their power regarding it. This portrait is in the Roman Catholic College at Blairs, near Aberdeen. It was in the Scotch College at Rome down to the period of the French occupation of that city in 1798, and formed part of the plunder from that college. It was subsequently discovered in a sale-room by the late Abbé Macpherson, rector of the same college, who purchased it and sent it to Blairs, where it has been for, now, a good many years. That it is a portrait of Beaton's time is certain; but the artist is unknown, and the picture has sustained damage. It is attributed, by a competent judge, who has himself painted two careful copies of it, to Titian, not only from its general style and handling, but from certain peculiarities of canvas, &c., on which latter circumstances, however, he does not lay much stress, taking them only as adminicles in proof. The portrait is a half-length, about 2 ft. 6 in. by 2 ft.: it is that of a fresh-coloured, intellectual man, of forty-five or upwards; hazel eyes; hair slightly reddish, or auburn, just becoming tinged with grey; a thin small beard; costume similar to that of Holbein's Cardinal Wolsey, in the hall of Christchurch, Oxford. It bears this inscription, painted at the bottom of the portrait, and over the original finished painting, and therefore of a subsequent date:
"David Betonius, S.R.E., Card. Archiep. S. Andreæ in Scotia, ab Hostibus Fidei Barbare Trucidatus."
Beaton was elected to the Cardinalate in Dec. 1538; did he visit Rome after that? He was at all events in Paris. The Scotch College at Rome was a natural habitat for a portrait of a Scottish churchman so famous as Cardinal Beaton, and it would be strange indeed if they had not one of him where they affected a collecion of portraits of British prelates. I propose to have this portrait engraved, if its probable authenticity cannot be shaken. Did Pinkerton engrave any portrait of Beaton? There is none in my copies of his Iconographia Scotica, 1797, and his Scottish Gallery, 1799. These contain several duplicates; but it is rare to meet with copies that can be warranted perfect. If the portrait be published, it will probably be accompanied by a short memoir, correcting from authentic documents some of the statements of his biographers: any information either as to the portrait or his life will be thankfully acknowledged. One or two letters from Lord Buchan, on the subject of Scottish Portraits, appeared in the Gentleman's Magazine, vol. lxv., but not relating to this particular one.
SCOTUS.ON THE POINTING OF A PASSAGE IN "ALL'S WELL THAT ENDS WELL."
Lafeu. "They say miracles are past: and we have our philosophical persons, to make modern and familiar, things, supernatural and causeless."—Act ii. Scene 3.
So the passage is pointed in Johnson and Steevens, that is, with a comma after the word "things;" and the same pointing is used in the recent editions of Mr. Knight, Barry Cornwall, and Mr. Collier.
It occurred to me that this pointing gave a meaning quite out of harmony with what directly follows, and also with the spirit in which Lafeu speaks. Let the comma be placed after "familiar", and the whole passage be read thus:
Lafeu. "They say miracles are past; and we have our philosophical persons to make modern and familiar, things supernatural and causeless. Hence is it, that we make trifles of terrors; ensconcing ourselves into seeming knowledge, when we should submit ourselves to an unknown fear."
Lafeu apparently is speaking somewhat sarcastically of those who say miracles are past, and who endeavour to explain away the wonderful into something common and well-known. Subsequently I found that Mr. Coleridge, in his Literary Remains (vol. ii. p. 121.), had adduced the above-mentioned passage, placing the comma after "familiar." He does not, however, make any observation on the other pointing; but remarking, that Shakspeare often uses "modern" for "common," proceeds thus:
"Shakspeare, inspired, as it might seem, with all knowledge, here uses the word causeless in its strict philosophical sense; cause being truly predicable only of phenomena,—that is, things natural, and not of noumena, or things supernatural."
It is, perhaps, rather curious, that although Mr. Collier, in his note on Lafeu's speech, has quoted the above from Mr. Coleridge, the improved pointing should have escaped that gentleman's notice.
Looking into Theobald's Shakspeare, I find that he also had placed the comma as Mr. Coleridge has. Mr. Theobald adds this note:
"This, as it has hitherto been printed, is directly opposite to our poet's and his speaker's meaning. As I have stopped it, the sense quadrates with the context: and surely it is one unalterable property of philosophy to make seeming strange and preternatural phenomena familiar and reducible to cause and reason."
Does not Mr. Theobald, in his closing remark, turn what in Lafeu is really an ironical outburst on would-be philosophers, into something like a serious common-place?
A. ROFFE.Query, In a work entitled Philosophy of Shakspeare, by W.H. Roukin, Lafeu's speech is quoted, and one word changed; "and we have our philosophical persons," &c., becomes "yet we have," &c. Is there any authority for such a change?
A.R.FOLK LORE
The bigger the Ring, the nearer the Wet.—On Sunday evening, the 20th Oct., the moon had a very fine ring round it, which apparently was based near the horizon, and spread over a considerable area of the heavens. This was noticed by myself and others as we returned home from church; and upon my mentioning it to my man-servant, who is a countryman, he said he had been noticing it, and that it reminded him of the old saying, "the bigger the ring, the nearer the wet." On the next day, however, it was fine and windy, and my faith began to be shaken as to the truth of the saying; but the almost incessant rain of the four or five subsequent days fully proved its correctness.
J.A.Power of prophesying before Death.—To the passages on this subject lately supplied by your correspondents (Vol. ii., pp. 116. 196.) may be added the following from Tertullian, De Anima, c. 53. (vol. ii. col. 741., ed. Migne, Paris, 1844):
"Evenit sæpe animam in ipso divortio potentius agitari, sollicitiore obtutu, extraordinariâ loquacitate, dum ex majori suggestu, jam in libero constituta, per superfluum quod adhuc cunctatur in corpore enuntiat quæ videt, quæ audit, quæ incipit nosse."
J.C.R.Change in the Appearance of the Dead.—A woman near Maidstone, who had had much experience as a sick-nurse, told me some years ago that she had always noticed in corpses a change to a more placid expression on the third day after death; and she supposed this to be connected with our Lord's resurrection. I omitted to ask her whether the belief were wholly the result of her own observation, or whether it had been taught her by others, and were common among her neighbours.
J.C.R.Strange Remedies.—I find some curious prescriptions in an old book entitled The Pathway to Health, &c. (I will not trouble you with the full title), "by Peter Levens, Master of Arts in Oxford, and Student in Physick and Chirurgery."… "Printed for J.W., and are to bee sold by Charles Tym, at the Three Bibles on London Bridge, MDCLXIV." The first is a charm
For all manner of falling evils.—Take the blood of his little finger that is sick, and write these three verses following, and hang it about his neck:
'Jasper fert Mirrham, Thus Melchior Balthazar Aurum,
Hæc quicum secum portat tria nomina regum,Soleitur à morbo, Domini pietate, caduca.'and it shall help the party so grieved."
"For a man or woman that is in a consumption.—Take a brasse pot, and fill it with water, and set it on the fire, and put a great earthen pot within that pot, and then put in these parcels following:—Take a cock and pull him alive, then flea off his skin, then beat him in pieces; take dates a pound, and slit out the stones, and lay a layer of them in the bottom of the pot, and then lay a piece of the cock, and upon that some more of the dates, and take succory, endive, and parsley roots, and so every layer one upon another, and put in fine gold and some pearl, and cover the pot as close as may bee with coarse dow, and so let it distill a good while, and so reserve it for your use till such time as you have need thereof."
I could select some exceedingly ludicrous prescriptions (for the book contains 400 pages), but the most curious unfortunately happen to be the most indelicate. Besides this, I am afraid the subject is scarcely worthy of much space in such an important and useful work as "NOTES AND QUERIES."
ALEXANDER ANDREWS.Abridge, Essex.
Mice as a Medicine (Vol. i., p. 397.).—An old woman lately recommended an occasional roast mouse as a certain cure for a little boy who wetted his bed at night. Her own son, she said, had got over this weakness by eating three roast mice. I am told that the Faculty employ this remedy, and that it has been prescribed in the Oxford Infirmary.
J.W.H.Omens from Birds.—It is said that for a bird to fly into a room, and out again, by an open window, surely indicates the decease of some inmate. Is this belief local?
J.W.H.MODE OF COMPUTING INTEREST
The mode of computing interest among the ancient Greeks appears to have been in many respects the same as that now prevailing in India, which has probably undergone no change from a very remote period. Precisely the same term, too, is used to denote the rate of interest, namely, τοκος in Greek and taka or tuka in the languages of Western India. Τοκοε επιδεκατοι in Greek, and dus také in Hindostanee, respectively denote ten per cent. At Athens, the rate of interest might be calculated either by the month or by the year—each being expressed by different terms (Böckh. Pub. Econ. of Athens, i. 165.). Precisely the same system prevails here. Pono taka, that is, three quarters of a taka, denotes ¾ per cent. per month. Nau také, that is, nine také, denotes nine per cent. per annum. For the Greek mode of reckoning interest by the month, see Smith's Dictionary of Greek and Roman Antiquities, p. 524. At Athens, the year, in calculating interest, was reckoned at 360 days (Böckh, i. 183.). Here also, in all native accounts-current, the year is reckoned at 360 days.
The word τοκος, as applied to interest, was understood by the Greeks themselves to be derived from τικτω, "to produce," i.e. money begetting money; the offspring or produce of money lent out. Whether its identity may not be established with the word in current use for thousands of years in this country to express precisely the same meaning, is a question I should like to see discussed by some of your correspondents. The word taka signifies any thing pressed or stamped, anything on which an impression is made hence a coin; and is derived from the Sanscrit root
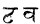
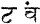
ON THE CULTIVATION OF GEOMETRY IN LANCASHIRE
If our Queries on this subject be productive of no other result than that of eliciting the able and judicious analysis subsequently given by MR. WILKINSON (Vol. ii., p. 57.), they will have been of no ordinary utility. The silent early progress of any strong, moral, social, or intellectual phenomenon amongst a large mass of people, is always difficult to trace: for it is not thought worthy of record at the time, and before it becomes so distinctly marked as to attract attention, even tradition has for the most part died away. It then becomes a work of great difficulty, from the few scattered indications in print (the books themselves being often so rare1 that "money will not purchase them"), with perhaps here and there a stray letter, or a metamorphosed tradition, to offer even a probable account of the circumstances. It requires not only an intimate knowledge of the subject-matter which forms the groundwork of the inquiry, both in its antecedent and cotemporary states, and likewise in its most improved state at the present time; it also requires an analytical mind of no ordinary powers, to separate the necessary from the probable; and these again from the irrelevant and merely collateral.
MR. WILKINSON has shown himself to possess so many of the qualities essential to the historian of mathematical science, that we trust he will continue his valuable researches in this direction still further.
It cannot be doubted that MR. WILKINSON has traced with singular acumen the manner in which the spirit of geometrical research was diffused amongst the operative classes, and the class immediately above them—the exciseman and the country schoolmaster. Still it is not to be inferred, that even these classes did not contain a considerable number of able geometers anterior to the period embraced in his discussion. The Mathematical Society of Spitalfields existed more than half a century before the Oldham Society was formed. The sameness of pursuit, combined with the sameness of employment, would rather lead us to infer that geometry was transplanted from Spitalfields to Manchester or Oldham. Simpson found his way from the country to London; and some other Simpson as great as Thomas (though less favourably looked upon by fortune in furnishing stimulus and opportunity) might have migrated from London to Oldham. Or, again, some Lancashire weaver might have adventured to London (a very common case with country artisans after the expiration of apprenticeship); and, there having acquired a taste for mathematics, as well as improvement in his mechanical skill, have returned into the country, and diffused the knowledge and the tastes he took home with him amongst his fellows. The very name betokens Jeremiah Ainsworth to have been of a Lancashire family.
But was Ainsworth really the earliest mathematician of his district? Or, was he merely the first that made any figure in print as a correspondent of the mathematical periodicals of that day? This question is worthy of MR. WILKINSON's further inquiry; and probably some light may be thrown upon it by a careful examination of the original Ladies' and Gentleman's Diaries of the period. In the reprints of these works, only the names, real or assumed, of those whose contributions were actually printed, are inserted—not the list of all correspondents.
Now one would be led to suppose that the study of mathematics was peculiarly suited to the daily mode of life and occupation of these men. Their employment was monotonous; their life sedentary; and their minds were left perfectly free from any contemplative purpose they might choose. Algebraic investigation required writing: but the weaver's hands being engaged he could not write. A diagram, on the contrary, might lie before him, and be carefully studied, whilst his hands and feet may be performing their functions with an accuracy almost instinctive. Nay more: an exceedingly complicated diagram which has grown up gradually as the result of investigations successively made, may be carried in the memory and become the subject of successful peripatetic contemplation. On this point a decided experimental opinion is here expressed: but were further instances asked for, they may be found in Stewart, Monge, and Chasles, all of whom possessed this power in an eminent degree. Indeed, without it, all attempts to study the geometry of space (even the very elements of descriptive geometry, to say nothing of the more recondite investigations of the science) would be entirely unproductive. It is, moreover, a power capable of being acquired by men of average intellect without extreme difficulty; and that even to the extent of "mentally seeing" the constituent parts of figures which have never been exhibited to the eye either by drawings or models.
That such men, if once imbued with a love for geometry, and having once got over the drudgery of elementary acquisition, should be favourably situated for its cultivation, follows as a matter of course. The great difficulty lay in finding sufficient stimulus for their ambition, good models for their imitation, and adequate facilities for publishing the results at which they had arrived. The admirable history of the contents of their scanty libraries, given by MR. WILKINSON, leaves nothing more to be said on that head; except, perhaps, that he attributes rather more to the influences of Emerson's writings than I am able to do.2 As regards their facilities for publication, these were few, the periods of publication being rarely shorter than annual; and amongst so many competitors, the space which could be allotted to each (even to "the best men") was extremely limited. Yet, contracted as the means of publication were, the spirit of emulation did something; from the belief that insertion was an admitted test of superiority, it was as much an object of ambition amongst these men to solve the "prize question" as it was by philosophers of higher social standing to gain the "prize" conferred by the Académie des Sciences, or any other continental society under the wing of Royalty, at the same period. The prize (half a dozen or a dozen copies of the work itself) was not less an object of triumph, than a Copley or a Royal medal is in our own time amongst the philosophers of the Royal Society.
These men, from similarity of employment and inevitable contiguity of position, were brought into intercourse almost of necessity, and the formation of a little society (such as the "Oldham") the natural result—the older and more experienced men taking the lead in it. At the same time, there can be little doubt that the Spitalfields Society was the pattern after which it was formed; and there can be as little doubt that one or more of its founders had resided in London, and "wrought" in the metropolitan workshops. Could the records of the "Mathematical Society of London" (now in the archives of the Royal Astronomical Society) be carefully examined, some light might be thrown upon this question. A list of members attending every weekly meeting, as well as of visitors, was always kept; and these lists (I have been informed) have been carefully preserved. No doubt any one interested in the question would, upon application to the secretary (Professor De Morgan), obtain ready access to these documents.
The preceding remarks will, in some degree, furnish the elements of an answer to the inquiry, "Why did geometrical speculation take so much deeper root amongst the Lancashire weavers, than amongst any other classes of artisans?" The subject was better adapted to the weaver's mechanical life than any other that could be named; for even the other favourite subjects, botany and entomology, required the suspension of their proper employment at the loom. The formation of the Oldham Society was calculated to keep alive the aspiration for distinction, as well as to introduce novices into the arcanium of geometry. There was generous co-operation, and there was keen competition,—the sure stimulants to eminent success. The unadulterated love of any intellectual pursuit, apart from the love of fame or the hope of emolument, is a rare quality in all stages of society. Few men, however, seem to have realised Basil Montagu's idea of being governed by "a love of excellence rather than the pride of excelling," so closely as the Lancashire geometers of that period—uncultivated as was the age in which they lived, rude as was the society in which their lives were passed, and selfish as the brutal treatment received in those days by mechanics from their employers, was calculated to render them. They were surrounded, enveloped, by the worst social and moral influences; yet, so far as can now be gathered from isolated remarks in the periodicals of the time, they may be held up as a pattern worthy of the imitation of the philosophers of our own time in respect to the generosity and strict honour which marked their intercourse with one another.
Mathematicians seldom grow up solitarily in any locality. When one arises, the absence of all external and social incentives to the study can only betoken an inherent propensity and constitutional fitness for it. Such a man is too much in earnest to keep his knowledge to himself, or to wish to stand alone. He makes disciples,—he aids, encourages, guides them. His own researches are fully communicated; and this with a prodigality proportioned to his own great resources. He feels no jealousy of competition, and is always gratified by seeing others successful. Thus such bodies of men are created in wonderfully short periods by the magnanimous labours of one ardent spirit. These are the men that found societies, schools, sects; wherever one unselfish and earnest man settles down, there we invariably find a cluster of students of his subject, that often lasts for ages. Take, for instance, Leeds. There we see that John Ryley created, at a later period, the Yorkshire school of geometers; comprising amongst its members such men as Swale, Whitley, Ryley ("Sam"), Gawthorp, Settle, and John Baines. This, too, was in a district in many respects very analogous to Lancashire, but especially in the one to which the argument more immediately relates:—it was a district of weavers, only substituting wool for cotton, as cotton had in the other case been substituted for the silk of Spitalfields.









