Революция разума: на подступах к Сингулярности. Как технологии изменят общество и сознание

Исследователей необычайно воодушевила новая научная формулировка давнего философского вопроса. В 1956 году математик Джон Маккарти (1927–2011) предложил провести двухмесячное исследование в Дартмутском колледже в Гановере, Нью-Гэпмшир, силами группы из десяти специалистов3. Вот как была сформулирована задача:

Исследование имеет своей целью проверить гипотезу, что способность к обучению или любое другое свойство интеллекта могут быть настолько тщательно формализованы, что машина сможет их имитировать. Будет предпринята попытка заставить компьютер пользоваться письменной речью, оперировать абстрактными понятиями, решать задачи, с которыми на данный момент может справиться только человек, а также научить программу совершенствовать саму себя4.

В преддверии конференции Маккарти предложил назвать новую область науки, благодаря которой впоследствии будут автоматизированы многие процессы, «искусственным интеллектом»5. Я не большой поклонник этого названия, поскольку из-за него создаваемый нами разум кажется как будто ненастоящим, но именно этот термин прижился в компьютерных науках.

Исследование провели, но цели, а именно: создать вычислительную машину, способную решить задачу, сформулированную на простом человеческом языке, конечно, за отведенные два месяца не достигли. Собственно, мы до сих пор занимаемся созданием такого компьютера, причем гораздо большими силами, чем десять исследователей. По данным китайского технологического гиганта Tencent, в 2017 году количество специалистов в области искусственного интеллекта во всем мире достигло 300 0006, а в 2019 году в «Обзоре специалистов в области ИИ по всему миру» его авторы Жан-Франсуа Ганье, Грейс Кизер и Йоан Манта насчитали 22 400 экспертов, публикующих статьи с оригинальными исследованиями в области ИИ, из которых 4000 были признаны весьма влиятельными7. По данным Стэнфордского института искусственного интеллекта, ориентированного на человека (Stanford HAI), в 2021 году разработчики ИИ опубликовали более 496 000 статей и подали более 141 000 заявок на патенты8. В 2022 году корпоративные инвестиции в ИИ по всему миру составили 189 миллиардов долларов, увеличившись в 13 раз за прошедшее десятилетие9. К моменту выхода этой книги суммы будут еще более внушительными.

Все это сложно было себе представить в 1956-м, когда участники Дартмутской конференции поставили перед собой задачу, которая не уступала по сложности созданию ИИ, способного пройти тест Тьюринга. Я уверен, что мы достигнем этого уже к 2029 году, и я не изменил своего прогноза, который опубликовал в 1999 году в книге «Век духовных машин»10. В те времена многие обозреватели сходились во мнении, что такого уровня технологий мы не достигнем никогда. Даже совсем недавно коллеги по отрасли считали мой прогноз чересчур оптимистичным. Например, опрос, проведенный в 2018 году, показал, что в среднем эксперты в сфере ИИ считают, что вычислительные машины не достигнут уровня человеческого интеллекта раньше 2060 года11. Однако в свете последних успехов в разработке больших языковых моделей многие ученые скорректировали свои ожидания. Когда я писал черновик этой книги, на сайте платформы для прогнозов Metaculus мнения относительно времени создания достаточно мощного ИИ колебались от 2040-х до 2050-х годов. Но темпы прогресса в последние два года вновь превзошли ожидания, и к маю 2022 года консенсус среди участников на Metaculus стал соответствовать обозначенной мной дате: 2029 год12. С тех пор высказывались и более смелые мнения, в частности, говорили о 2026 годе, так что технически мой изначальный прогноз теперь можно считать консервативным13.

Последнее время новые достижения в сфере ИИ поражают даже экспертов. Открытия не только происходят раньше, чем ожидалось, но главное, что они случаются внезапно, а не назревают в течение долгого времени. Например, в октябре 2014-го Томазо Поджио, эксперт по ИИ и когнитивной нейробиологии из Массачусетского технологического института, отвечая на вопрос журналиста, сказал: «Задача описать, что изображено на картинке, будет одной из самых сложных для искусственного интеллекта. Чтобы приблизиться к ее решению, нам потребуется провести еще множество фундаментальных исследований»14. Согласно оценке Поджио, этот рубеж должен был покориться нам лет через двадцать. Через месяц после этого интервью компания Google представила ИИ, умеющий решать ровно эту задачу – распознавать объекты на изображении. Когда обозреватель журнала New Yorker Раффи Хачадурян попросил Поджио прокомментировать это событие, тот в ответ высказал сомнение, что эта способность отражает наличие истинного интеллекта. Я пишу это не в качестве критики, а как пример общей тенденции. А именно: пока у ИИ не получается решить определенную задачу, нам кажется, что она необычайно сложна и под силу только человеку. Однако как только компьютер с ней справляется, мы склонны обесценивать это достижение. Иначе говоря, мы добились гораздо больших успехов, чем нам самим кажется задним числом. Это одна из причин, почему я не теряю веры в свой прогноз насчет 2029 года.

Почему эти открытия оказались столь неожиданными? Чтобы ответить на этот вопрос, нужно вспомнить одну дилемму, стоявшую перед теоретиками на заре развития отрасли. В 1964 году, еще будучи школьником, я познакомился с двумя выдающимися представителями направления ИИ: Марвином Минским (1927–2016), который был одним из организаторов той лаборатории по ИИ в Дартмутском колледже, и Фрэнком Розенблаттом (1928–1971). В 1965 году я поступил в МТИ, где моим научным руководителем стал Минский. В то время он занимался фундаментальными исследованиями, которые и заложили основы для резкого скачка в развитии нейросетей, произошедшего в последние годы. От него я узнал, что существуют два подхода к автоматизации решения задач: символьный и нейросетевой (так называемый «коннекционизм»).

Символьный подход опирается на перечисление правил, по которым человек, являющийся экспертом, решал бы поставленную задачу. Иногда такой подход себя оправдывает. Например, в 1959 году корпорация RAND представила «Универсальный решатель задач» – компьютерную программу, способную оперировать простыми математическими аксиомами и находить решение логических задач15. Герберт Саймон, Клиффорд Шоу и Аллен Ньюэлл разработали «Универсальный решатель», чтобы получить возможность решать любую задачу, которую можно сформулировать в терминах нормальных форм алгебры высказываний. Чтобы решить задачу, программа обрабатывала одну формулу (аксиому) на каждом этапе процесса, постепенно выстраивая с их помощью доказательство теоремы.

Даже если вы не знакомы с формальной логикой или теорией доказательств, понять этот принцип можно на примере алгебры. Если известно, что 2 + 7 = 9 и что к неизвестному числу прибавили 7 и получили 10, можно показать, что искомое число равно 3. Но таким путем можно получать и более сложные результаты. Когда мы задаемся вопросом, соответствует ли некий объект заданному определению, то руководствуемся такой же логикой, даже не отдавая себе в этом отчета. Допустим, мы знаем, что простое число не имеет делителей, кроме 1 и самого себя, а также, что число 11 делит число 22 пополам. Учитывая, что 1 не равно 11, мы можем заключить, что 22 не является простым числом. Имея в распоряжении самые простые и фундаментальные аксиомы, УРЗ может применить подобные рассуждения к существенно более сложным задачам. Математики, строго говоря, именно этим и занимаются, только компьютер в поисках ответа в состоянии (теоретически, по крайней мере) сопоставить аксиомы друг с другом всеми возможными способами.

Представим для наглядности, что у нас есть 10 аксиом, а для решения задачи нужно выбрать одну из них на каждом из 20 шагов. В таком случае существует 1020, то есть миллиард раз по 100 миллиардов возможных вариантов решения. В настоящее время мы можем работать с такими величинами, но у компьютеров 1959 года шансов справиться не было. Электронная вычислительная машина DEC PDP-1 могла выполнять 100 000 операций в секунду16. В 2023-м облачный сервер Cloud A3 компании Google способен совершать примерно 26 000 000 000 000 000 000 операций в секунду17. Сейчас один доллар обеспечит в 1,6 триллиона раз больше вычислительной мощности, чем во времена УРЗ18. На решение задач, с которыми современные домашние компьютеры справляются за несколько минут, у машин 1959 года ушли бы десятки тысяч лет. В попытке преодолеть вычислительные ограничения в УРЗ встроили эвристические алгоритмы, которые ранжировали возможные решения, отдавая приоритет наиболее перспективным. Иногда это срабатывало, и каждый успех вселял надежду, что рано или поздно компьютер сможет решить любую должным образом сформулированную задачу.

Еще одним примером может служить система МИЦИН, разработанная в 1970-х годах для диагностики инфекционных заболеваний и выдачи рекомендаций по лечению. В 1979 году группа экспертов сравнила результаты этой программы с назначениями докторов, и оказалось, что МИЦИН справилась с задачей как минимум не хуже, а иногда и более успешно, чем настоящий врач19.

Типичное «правило» в программе МИЦИН выглядело так:

ЕСЛИ:

1) Заболевание, требующее лечения, – это менингит, и

2) тип инфекции – грибковая, и

3) посев не выявил роста микроорганизмов, и

4) пациент не является ослабленным, и

5) пациент побывал в районе, эндемичном по кокцидиомикозам, и

6) пациент принадлежит к одной из следующих расовых групп: афроамериканцы, азиаты, индейцы, и

7) анализ ликвора на криптококковый антиген не был положительным,

ТОГДА:

Предположительно (с вероятностью 50 %) криптококк не является одним из организмов (помимо тех, которые обнаружились в посевах или мазках), вызвавших заболевание20.

К концу 1980-х годов так называемые «экспертные системы», подобные МИЦИН, начали использовать вероятностные модели и стали учитывать множество источников информации при принятии решений21. В сложных случаях одним правилом типа «если… то» не обойтись, но, скомбинировав тысячи таких логических утверждений, в рамках определенного класса задач система могла предложить достаточно надежное решение.

В рамках символьного подхода исследователи работали более полувека, но не нашли способа преодолеть «потолок сложности»22. Когда МИЦИН или подобные системы допускали ошибку, она поддавалась исправлению, но решение одной проблемы порождало три новые ошибки в других ситуациях. Усложнять экспертную систему удавалось лишь до определенного предела, из-за чего диапазон реальных задач, которые с таким подходом можно было решать, оказывался весьма узким.

Можно рассматривать сложность экспертных систем на основе правил с точки зрения точек отказа. Известно, что количество подмножеств у множества из n-элементов составляет 2n – 1 (не считая пустое множество). Если набор правил ИИ состоит из одного закона, то существует всего одна точка отказа: корректно это правило само по себе или нет. Если правила два, точек отказа будет уже три: две соответствуют каждому из правил в отдельности, а третья относится к их комбинации. С ростом количества правил число возможных точек отказа растет экспоненциально. Пять правил порождают 31 точку отказа, 10 правил – 1023; 100 правил – и точек отказа уже больше тысячи миллиардов умножить на миллиард и еще раз умножить на миллиард, а 1000 правил дают больше гугол умножить на гугол умножить на гугол точек отказа. Из этого, в частности, следует, что чем больше у вас в системе правил, тем больше возможных точек отказа добавит каждое дополнительное правило. Даже если ничтожно малая доля комбинаций из правил работает некорректно, рано или поздно наступит момент (когда конкретно, зависит от задачи), когда добавление нового правила, которое решает проблемную ситуацию, приведет к появлению более одной новой проблемы. Такую ситуацию и называют потолком сложности.

Вероятно, из подобных экспертных систем дольше всего разрабатывалась Cyc (от слова encyclopedic – «энциклопедический»), созданная Дугласом Ленатом и его коллегами по компании Cycorp в 1984 году23. Разработчики преследовали цель зафиксировать все соображения здравого смысла, которые известны людям, например, «брошенное на пол яйцо разобьется» или «ребенок, бегающий по кухне в грязной обуви, вызовет недовольство родителей». Миллионы соображений подобного рода нигде не зафиксированы, но при этом необходимы для понимания того, чем руководствуется среднестатистический человек. Однако, поскольку Cyc хранила эти знания в виде набора правил, она также оказалась подвержена проблеме потолка сложности.

В 1960-х годах мы с Минским обсуждали достоинства и недостатки символьного подхода к созданию ИИ, и в сравнении я начал осознавать преимущества сетевой парадигмы. Коннекционизм подразумевает использование сети простых узлов, которая приобретает функции интеллекта благодаря своей структуре, а не информации в отдельных узлах. Вместо сложных правил система опирается на узлы, которые сами по себе почти ничего не умеют, но, объединенные в большую сеть, способны извлекать информацию из поступающих данных. Благодаря этому такие сети способны находить закономерности, которые никогда не пришли бы в голову программистам, если бы те попытались применить символьный подход. Одним из основных преимуществ сетевого подхода является то, что с его помощью можно решать задачи, не имея готового метода. Ведь даже если бы мы в совершенстве владели навыком правильно формулировать и безошибочно переносить в программу необходимые для работы ИИ правила (а это большое «если»), нам бы все равно мешало отсутствие четкого понимания, какие из них стоит вносить в программу.

Нейронная сеть – это мощный инструмент для решения сложных задач, однако он не лишен недостатков. Построенный по такому принципу искусственный интеллект имеет обыкновение превращаться в «черный ящик». ИИ дает нам ответ, но не в состоянии пояснить, как он пришел именно к такому варианту24. Это свойство угрожает стать серьезной проблемой, поскольку людям хочется знать обоснование принятых решений по важным вопросам, таким как выбор метода лечения, обеспечение соблюдения норм правопорядка, гигиенический надзор, управление рисками. Вот почему в настоящее время ряд экспертов в области ИИ работает над повышением «прозрачности» результатов работы нейросетей (так называемой «механистической интерпретабельности»), иначе говоря, возможности раскрыть причинно-следственные связи, стоящие за их решениями25. Пока неясно, насколько эта цель достижима, учитывая, что многослойные нейросети становятся все более сложными и мощными.

Когда я начинал работать с нейронными сетями, их устройство было гораздо более простым. В основе технологии лежала идея создать компьютерную модель того, как работает центральная нервная система человека. Поначалу это было довольно туманное соображение, потому что моделирование началось еще до того, как ученые смогли более-менее подробно изучить, каким образом организованы сети нейронов в биологическом мозге.

Схема простой нейронной сети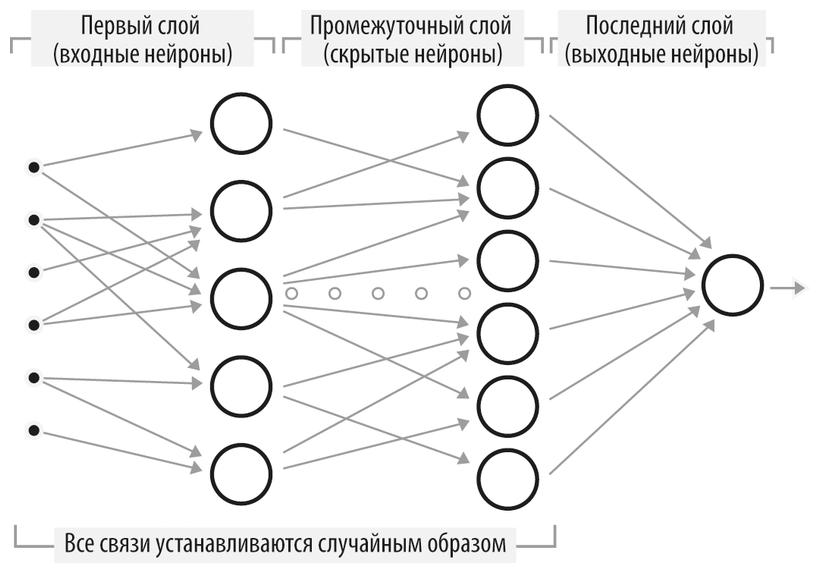

Приведем описание типичного алгоритма на основе нейронной сети. В зависимости от конкретной задачи этот алгоритм может принимать множество форм, но в любом случае при создании системы необходимо выбрать подходящие методы и установить значения ключевых параметров.

Чтобы создать решение на основе нейронной сети, нужно пройти через несколько этапов:

– Определить, какие данные будут использоваться в качестве входных.

– Разработать структуру нейронной сети (то есть задать количество и размеры слоев, а также связи между нейронами).

– Обучить нейросеть на данных с известными ответами.

– Использовать нейросеть для решения новых задач.

– Опубликовать результаты и открыть доступ к своему сервису.

Рассмотрим каждый из этих шагов (кроме последнего) подробнее.

Входные данные

Входные данные задачи, поступающие в нейронную сеть, состоят из ряда чисел. Нейросеть может обрабатывать:

– В задачах распознавания визуальных образов: изображения, представленные в виде двумерного массива чисел, соответствующих пикселям.

– В задачах обработки аудиосигнала (например, речи): звук, представленный в виде двумерного массива чисел, одно измерение в котором соответствует точкам на временной шкале, а второе – характеристикам звука (например, частотным составляющим).

– В задачах распознавания образов произвольной природы: многомерный массив чисел, характеризующих входной образ.

Определение структуры сети

Архитектура нейронной сети определяется связями каждого из нейронов:

– Каждое «входящее» соединение нейрона обычно связано с «исходящим» соединением другого нейрона либо с одним из входных значений набора данных.

– Как правило, единственное «исходящее» соединение служит для передачи результата работы данного нейрона другому, находящемуся в более высоком слое, либо сообщает результат работы всей нейронной сети.

Создание входного слоя нейронов

– Первый слой содержит N0 входных нейронов. Входящие соединения каждого из них связаны с «точками» (то есть числами) из массива входных данных. Количество и структура этих связей могут быть установлены произвольно либо определены с помощью генетического алгоритма (см. описание ниже).

– Для каждого соединения необходимо задать «силу синаптической связи». Начальные значения «весов» связей могут быть равны какому-то одному числу, или заданы случайным образом, или определены каким-либо еще способом.

Создание внутренних слоев нейронов

Необходимо создать M скрытых слоев. В каждом из внутренних слоев:

– Создается Ni нейронов (где i – номер слоя). Входящие соединения каждого из них связываются с исходящими соединениями нейронов в предыдущем слое (см. также раздел «Вариации»).

– Задаются начальные значения «весов» связей, равные какому-то одному числу, определенные случайным образом или другим способом (см. ниже).

– Выходные соединения нейронов в слое с номером M передают итоговый результат работы нейронной сети (см. раздел «Вариации»).

Процесс распознавания

Принцип работы нейрона

Каждый нейрон по ходу одного цикла работы нейросети совершает следующие операции:

– Умножает каждый входящий сигнал (то есть числовое значение, поступившее от нейрона в предыдущем слое либо из массива входных данных) на вес соответствующей синаптической связи.

– Суммирует все входящие взвешенные сигналы.

– Если полученная сумма больше порога активации данного нейрона, нейрон возбуждается и посылает исходящий сигнал, равный единице, иначе исходящий сигнал равен нулю (см. раздел «Вариации» ниже).

Получение результата работы нейросети

Во всех слоях от входного до выходного каждый нейрон выполняет следующие действия:

– Вычисляет взвешенную сумму входящих сигналов (то есть исходящих сигналов нейронов предыдущего слоя либо чисел из массива входных данных).

– Если взвешенная сумма входящих сигналов больше порогового значения для нейрона, исходящий сигнал принимается равным единице, иначе нулю.

Процесс обучения нейронной сети

– Раз за разом проводится процесс распознавания на примерах из обучающей выборки.

– После каждого цикла работы нейросети веса синаптических связей между всеми нейронами корректируются так, чтобы улучшить точность ответов нейросети на данной выборке примеров (о том, как это происходит, рассказано далее).

– Обучение продолжается до тех пор, пока точность работы нейросети на обучающей выборке не перестанет расти (то есть не приблизится к предельным для данных условий значениям).

Ключевые аспекты проектирования

Приведенная выше простая схема требует от разработчика принятия нескольких решений в самом начале работы:

– Каким аспектам задачи будут соответствовать числа, подаваемые на вход нейронной сети.

– Каким будет количество слоев.

– Сколько нейронов будет в каждом слое (это число может быть различным для разных слоев).

– Сколько входящих соединений будет у нейронов в каждом слое. Это количество тоже может отличаться от слоя к слою и даже от нейрона к нейрону внутри одного слоя.

– Какой будет сама структура связей. Для каждого нейрона необходимо составить список нейронов, исходящие соединения которых будут являться входящими для данного. Это одна из самых важных задач при проектировании. Ее можно решить разными путями:

1. Назначить соединения случайным образом.

2. Использовать генетический алгоритм (см. ниже) для определения оптимальной схемы.

3. Задать топологию на усмотрение разработчика.

– Какими будут начальные значения весов всех синаптических связей. Они могут быть определены разными способами:

1. Установлены равными какому-то одному значению.

2. Определены случайным образом.

3. Найдены с помощью генетического алгоритма.

4. Установлены согласно представлениям разработчика.

– Каков будет порог активации для каждого нейрона.

– В какой форме нейросеть будет давать ответ. Результатом ее работы может быть:

1. Массив сигналов нейронов выходного слоя.

2. Исходящий сигнал единственного нейрона, на вход которому подаются сигналы последнего слоя нейронов.

3. Результат вычисления определенной функции от исходящих сигналов нейронов последнего слоя, например, их сумма.

4. Результат вычисления определенной функции от исходящих сигналов нейронов нескольких слоев.

– Каким методом будут корректироваться синаптические веса в ходе обучения нейросети. Это один из ключевых моментов, которому посвящены многочисленные исследования и дискуссии. Отметим ряд важных моментов:

1. После каждого цикла работы нейросети можно поочередно увеличивать или уменьшать вес каждого соединения на малую величину и проверять, какое из этих изменений увеличивает точность работы. Это требует больших временных затрат, поэтому были разработаны способы предсказать сторону, в которую следует изменить вес конкретной связи.

2. Существуют специальные статистические методы коррекции весов после каждого цикла работы сети, позволяющие добиться того, чтобы сеть давала более точный ответ для текущего примера.

3. Заметим, что нейросеть может успешно обучаться даже при наличии ошибок в обучающей выборке примеров. Это позволяет использовать данные, собранные в реальном мире, в которых неизбежно присутствует доля ошибочно размеченных. Для достижения хотя бы удовлетворительных результатов обучения нейросети распознаванию образов очень важным условием является наличие большого количества тренировочных данных. Как и в случае с человеком, время, затраченное на обучение, имеет большое значение для качества итогового результата.

Вариации

Существует множество вариаций приведенной выше схемы:

– Топологию сети можно выбрать случайным образом или найти оптимальную схему связей между нейронами, применив генетический алгоритм, в котором используется подобие мутации и естественного отбора применительно к структуре сети.

– Веса можно устанавливать в соответствии с различными соображениями.

– Нейрон может получать сигналы не только с предыдущего уровня, но и от нейронов, находящихся на других уровнях, как выше, так и ниже его.

– Выходной сигнал нейросети может быть определен по-разному.

– В приведенном выше описании нейросети использована нелинейная функция активации нейрона, работающая по принципу «все или ничего». Существуют и другие варианты нелинейных функций активации. Обычно используется функция, при которой выходной сигнал также лежит в диапазоне от нуля до единицы, но его значение меняется немного плавнее, и, кроме того, он может принимать значения, отличные от 0 и 1.

– Разные методы корректировки весов в процессе обучения существенно влияют на работу нейросети.

Приведенная нами схема описывает функционирование «синхронной» нейронной сети. Каждый цикл ее работы состоит в последовательном вычислении сигналов нейронов, начиная с входного слоя и заканчивая выходным. В по-настоящему параллельных системах, в которых нейроны работают независимо друг от друга, работа идет в «асинхронном» режиме. При этом каждый нейрон непрерывно обрабатывает поступающие на вход сигналы, и как только их взвешенная сумма превысит пороговое значение (или будет выполнено другое заданное условие), срабатывает функция активации.

После того как мы спроектировали нейронную сеть, нам необходимо найти обучающую выборку, работая с которой нейронная сеть поймет, как решать задачу. Как правило, начальные значения весов и карта связей между нейронами задаются случайным образом. Поэтому ответы, которые дает эта необученная нейросеть, полностью бессистемны. Основная задача нейронных сетей – учиться работать с поступающей информацией. В этом смысле они похожи (хотя бы в первом приближении) на мозг млекопитающих, по аналогии с которым и разрабатывались. Сначала нейросеть абсолютно некомпетентна, единственное, на что она запрограммирована – добиваться максимального значения «функции вознаграждения». Ей на вход подаются обучающие данные, например, заранее отсортированные человеком фотографии, на которых есть корги, и те, на которых нет. Когда нейросеть дает верный ответ на вопрос, есть ли на изображении корги, она получает положительную обратную связь в виде более высоких значений функции вознаграждения. Исходя из этого нейросеть модифицирует силу взаимодействия между различными парами нейронов. Связи, которые способствовали получению верного ответа, становятся сильнее, а те, которые приводили к ошибкам, ослабляются.