Матрицы и программирование

Николай Морозов

Матрицы и программирование

Введение

Этой книгой я начинаю курс практических занятий по Линейной алгебре, которые я проводил со студентами университета культуры и искусств в городе Санкт – Петербурге. Параллельно с этим, на порталах «Инфоурок « и «Знание» появились и мои авторские материалы в виде статей, презентаций, рабочих программ и т. д.

1. Основные понятия

Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий.

Элементами матрицы могут являться числа, алгебраические символы или математические функции.

Матрицы широко используются для решения систем алгебраических и дифференциальных уравнений, шифрования сообщений в Интернете и т. д.

Таким образом, матрица обозначается одной из заглавных букв латинского алфавита, например A, а набор ее элементов помещается в круглые скобки:

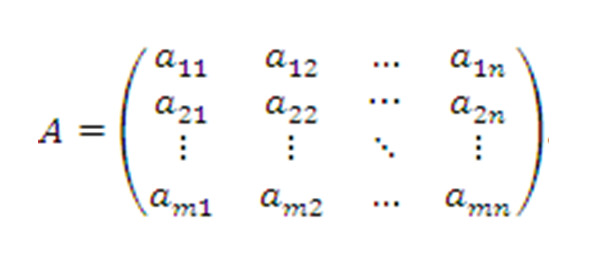
Формула матрицы

Представленная формулой (1) матрица A имеет m строк и n столбцов и называется m×n матрицей или матрицей размера m×n.

Строки матрицы нумеруются сверху вниз, а столбцы – слева направо (см. рис.1):

Рис.1.

Матричный элемент, расположенный на пересечении i-ой строки и j-го столбца, называется i,j-м элементом и записывается в виде aij, а выражение A = || ai ||j означает, что матрица A составлена из элементов aij. (см. рис.2):

Рис.2.

Матрица (см. рис.2.) размера 1×n называется матрицей-строкой или вектором-строкой.

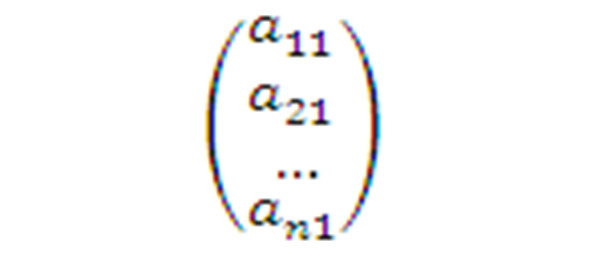
Рис.3.

Матрица (см. рис.3.) размера n×1 называется матрицей-столбцом или вектором-столбцом.

Для краткости вектор-строку и вектор-столбец обычно называют просто векторами.

Особую роль играют матрицы, у которых число строк совпадает с числом столбцов, то есть матрицы размера n×n. Такие матрицы называются квадратными (см. рис.4).

Рис.4.

При ссылке на квадратную матрицу достаточно указать ее порядок. Например, матрица третьего порядка имеет размер 3x3 (см. рис.5)

Рис.5.

Главная и побочная диагонали квадратной матрицы (рис.6).

Рис.6.

Примеры диагональных матриц второго и третьего порядков (рис.7)

Если у диагональной матрицы n – го порядка E все диагональные элементы = 1, то такая матрица называется единичной матрицей n – го порядка.

Если все недиагональные элементы квадратной матрицы = 0, то такая матрица называется диагональной.

Единичную матрицу обозначают буквой E или I (рис.8).

Рис.8.

Понятие нулевой или нуль – матрицы

Рис.9.

1.1.Равенство матриц

Матрицы A = || aij || и B = || aij || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:

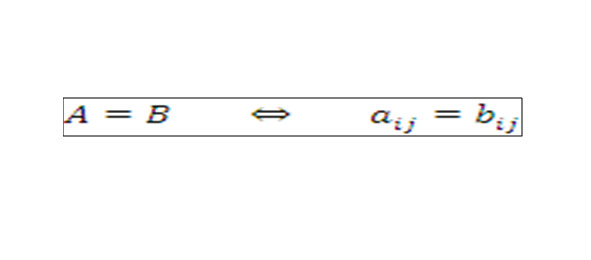
для любых допустимых значений индексов i и j.

1.2. Умножение матрицы на число

Умножать на число можно матрицу любого размера. При умножении матрицы A на число λ каждый ее матричный элемент умножается на это число (для любых допустимых значений индексов i и j).:

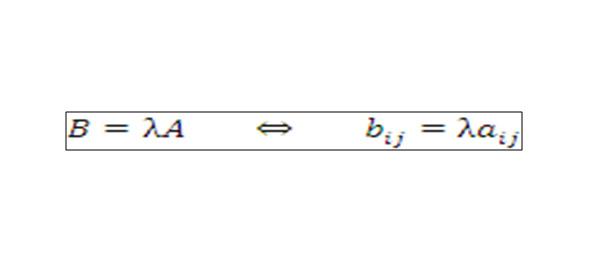
В результате получим новую матрицу В.

Нахождение новой матрицы путем умножения на число:

В результате получим матрицу 3A.

Вынесение общего можителя за знак матрицы.

1.3.Сложение матриц

Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || aij || и B = || bij || является матрица C = || cij ||, элементы которой равны сумме соответствующих матричных элементов:

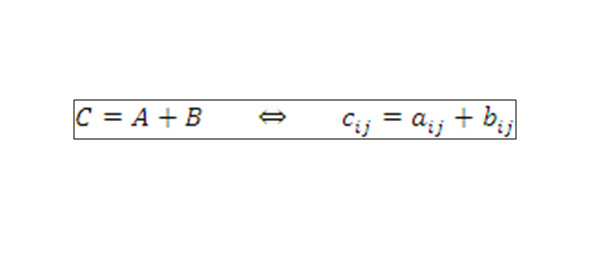
Результат сложения двух матриц.

Складывать (и вычитать) можно матрицы только одного размера!

Результат сложения двух матриц с учетом правила

A + 0 = A.

1.4.Вычитание матриц

Формула вычитания двух матриц иллюстрируется примерами 2.4 и 2.5.

1.5.Умножение строки на столбец

Пусть А = – матрица-строка размера 1×n, и пусть В – матрица-столбец размера n×1. (Иначе говоря, пусть число элементов в строке матрицы A совпадает с числом элементов в столбце матрицы B.)

Тогда произведением AB называется число, равное сумме попарных произведений соответствующих матричных элементов:

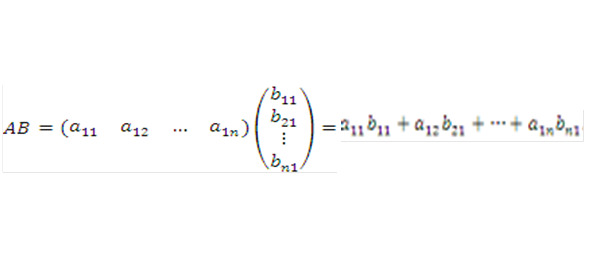
Формула является правилом умножения строки на столбец.

Если матрица A содержит m строк, а матрица B – n столбцов, то произведение AB представляет собой m×n матрицу, i,j-ый элемент которой вычисляется по правилу умножения i-ой строки матрицы A на j-ый столбец матрицы B. Например, при умножении двухстроковой матрицы:

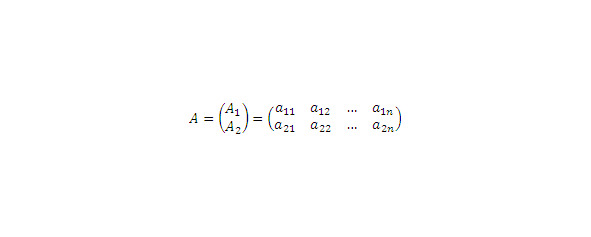
на матрицу-столбец B (см.рис.3) каждая из строк (A1 и A2) матрицы A поочередно умножается на столбец B.

Результатом произведения AB является матрица размера 2×1

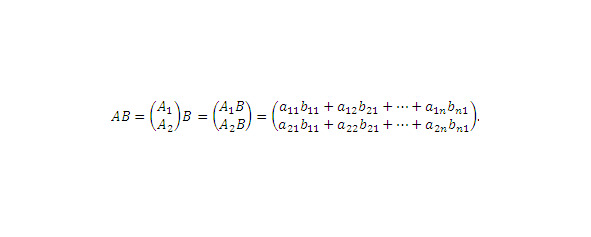
Результат произведения AB.

1.6. Умножение матриц

Перемножать матрицы можно только, если число столбцов первой матрицы равно числу строк второй!

Пусть – m×l матрица и пусть – l×n матрица.

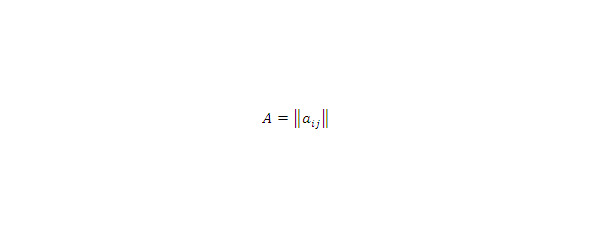
Матрица A.

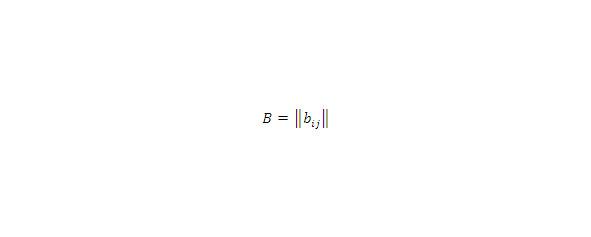
Матрица B.