Gold Trader. Связь между чётными степенями интеграла Гаусса, гамма-функцией и уровнями Фибоначчи

2. Разложение в цепную дробь

Число π можно представить в виде цепной дроби (continued fraction), что раскрывает его слоистую приближенную структуру:

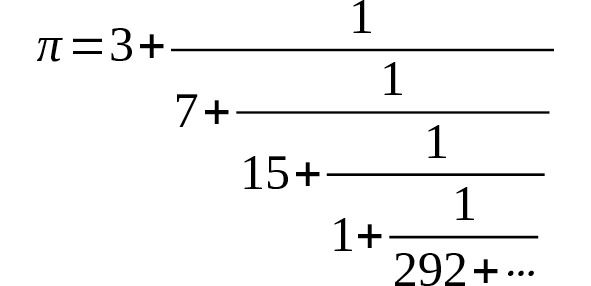
Этот ряд важен, потому что даёт лучшее из возможных приближений числом (например, 22/7, 333/106 и т.д.) [20] [21].

3. Разложения через бесконечные ряды

Существует множество разложений π в виде бесконечных рядов. Так, например, формула Лейбница:

или формула Грегори:

Того же типа – формулы Рамануджана, Чудновских и др., часто включающие факториалы, радикалы и числа Гамма-функции [22] [23].

4. Расслоение через интегралы и связанные функции

π можно определять как значение определённого интеграла, что приводит к его представлению через «слоистую» структуру функций:

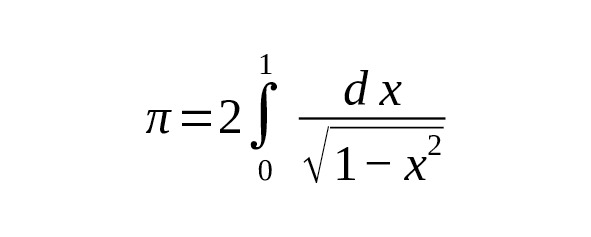
или

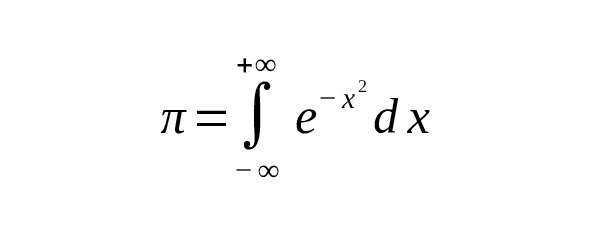
где роль слоёв играют элементарные и специальные функции – экспоненциальные, тригонометрические, а также Гамма-функция (например,) [22].

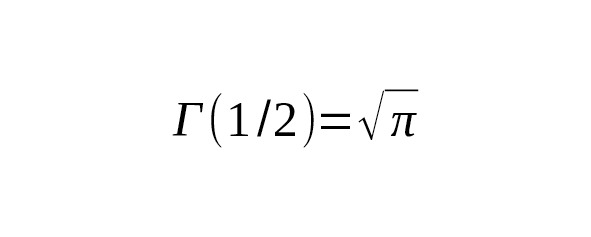
5. Связь с Гамма-функцией и функциональным анализом

Обобщённые разложения позволяют представить π как результат действия определённых операторов и преобразований:

– — связь с интегралом Гаусса.

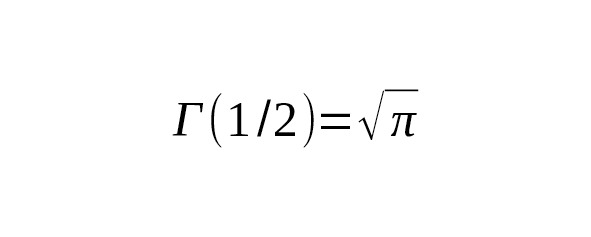
– Появление π в резонансных условиях (спектры колец, круговые интегралы и др.).

6. Алгебраическая и топологическая «структура» π

– Иррациональность: у π нет алгебраического представления в виде дроби (это иррациональное и, более того, трансцендентное число), его слой – вне «простых» чисел.

– Трансцендентность: π нельзя выразить с помощью корней и целых коэффициентов – это слой более высокой сложности, чем у большинства чисел [24] [22].