
Полная версия
Математика для тех, кто боится математики: Еще одна книга с дурацкими рисунками
Вот, например, отрицательные числа. Нельзя насчитать –3 собаки, пройти –3 километра или проспать –3 часа. В действительности никакое измерение никогда не даст результата в –3 (если только мы не смухлевали, написав «–3» на шкале термометра, хотя ртуть поднимается на положительное расстояние).
Если числа возникают в результате измерений, откуда тогда берется –3?

То же относится к иррациональным числам, таким как
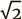
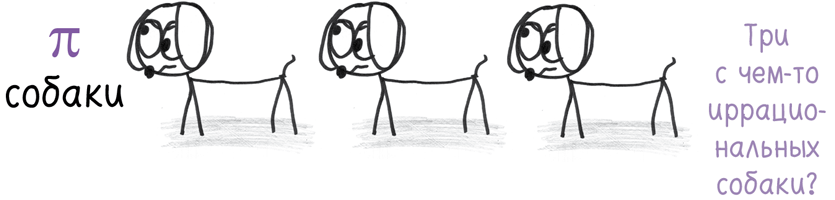
А есть еще мнимые числа (такие как i, квадратный корень из –1). Название «мнимые» первоначально возникло как бранное – его придумал математик, отказывавшийся верить, что такие числа существуют[11]. Их можно найти не только на числовой оси, но также над ней и под ней. Странно, правда? Это уж точно не результаты измерений. И все-таки это числа.
Или нет?
Да, числа. Отрицательные, иррациональные и мнимые числа возникают вполне естественным путем – не в результате самих измерений, а из закономерностей и расчетов, связанных с измерениями. Вычтите из пяти восемь, и – бам! – получится отрицательное число. Рассчитайте длину диагонали квадрата, и – бум! – длина выйдет иррациональной. Решите простое уравнение типа х2 = –1, и – бряк! – решением окажется мнимое число. Хотя язык чисел начинается с измерений, числа быстро начинают жить собственной жизнью.
Когда-нибудь моя дочь познает весь причудливый зоопарк неизмерительных чисел. Чуть раньше ей придется усвоить, что температура под мышкой не слишком точна, особенно в том, что касается определения роста и веса. Но пока я рад, что она уловила элементарную истину: математический язык начинается с того, что вы суете термометр под мышку реальности и вынимаете его, чтобы объявить число.
Отрицательные числа
В старшей школе у меня был одноклассник, печально известный своими дикими выходками, срывавшими нам уроки. «Смотрите, – однажды сказал он, – я кое-что привношу в наше обучение. Может быть, это и отрицательное число, но, как по мне, перед ним все равно стоит знак сложения»[12].
Мне всегда нравилась эта его реплика. Она передает дух отрицательных чисел: присутствие отсутствия. Избыток недостатка.
Отрицательные числа – лингвистический фокус, способ соединения противоположностей. Алиса говорит Черной Королеве: «Холм никак не долина. Это полная чепуха»[13][14]. Однако в случае с отрицательными числами холм и есть долина – точнее, долина и есть отрицательный холм. Вместо «100 м ниже уровня моря» или «5000 м над уровнем моря» можно назвать высоты –100 и +5000 (порой опуская плюс). Аналогичным образом, вместо «через 8 минут после запуска ракеты» или «за 15 минут до запуска» можно сказать «+8:00» и «–15:00». Некоторые слова («после», «выше», «вперед», «более») преобразуются в +, а их антонимы («до», «ниже», «назад», «менее») оборачиваются –.
Положительные и отрицательные числа представляют собой зеркальные отображения, которые соединяются и образуют совокупность, известную как числовая ось. Так как понятие числовой оси возникло в XVII в., новизна его теперь померкла – но не его значение[15].
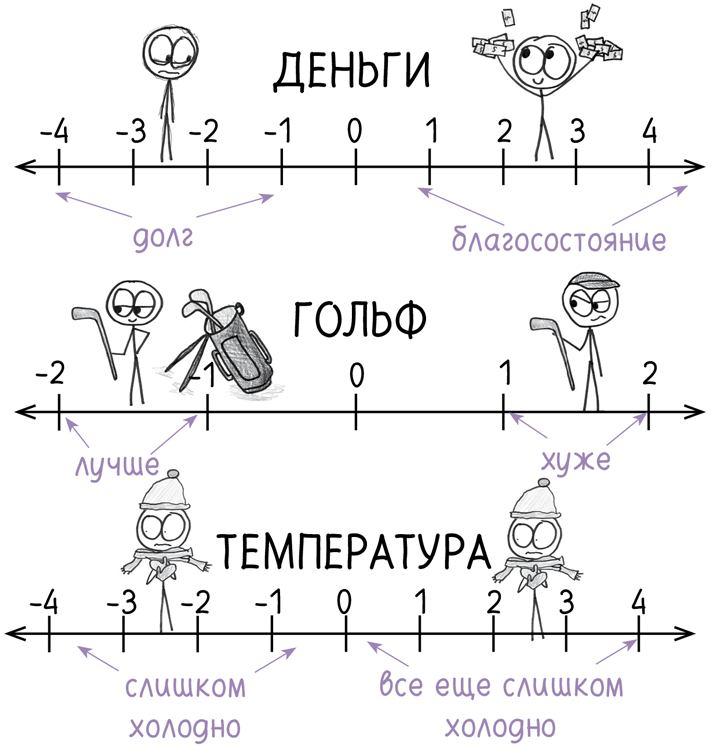
Ныне мы называем счетные числа (1, 2, 3 и т. д.) натуральными. Добавим сюда ноль и числа, противоположные натуральным (–1, –2, –3 и т. д.), и мы получим группу, которую называют целыми числами. Это все несложно. Так почему же математики веками отказывались признать отрицательные числа за настоящие? Почему Михаэль Штифель называл их «нелепыми» и «выдуманными»[16]? Почему Бхаскара отмечал, что «людям они не нравятся»[17]? Почему Фрэнсис Мейзерис считал их «полной чепухой или невразумительным жаргоном»[18]
Конец ознакомительного фрагмента.
Текст предоставлен ООО «Литрес».
Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Notes
1
Перевод А. Н. Анваера. – Прим. пер.
2
Oliver Sacks, Seeing Voices: A Journey into the World of the Deaf (Berkeley: University of California Press, 1989). Сакс говорит не конкретно о математическом языке, но о природе владения любым языком.
3
Albert Einstein, “The Late Emmy Noether,” The New York Times, May 4, 1935.
4
Karen Olsson, The Weil Conjectures: On Math and the Pursuit of the Unknown (New York: Farrar, Straus and Giroux, 2019).
5
Сноудония – горный регион и национальный парк в Северном Уэльсе. – Прим. пер.
6
Jorge Luis Borges, Collected Fictions (London: Penguin Putnam, 1998).
7
Перевод Е. М. Лысенко. – Прим. пер.
8
Перевод Л. Н. Ляховой. – Прим. пер.
9
Ursula Le Guin, A Wizard of Earthsea (New York: Houghton Mifflin, 1968).
10
См., например, Alice Clapman and Ben Goldstein, “Hand-Counting Votes: A Proven Bad Idea,” Brennan Center for Justice, November 23, 2022, https://www.brennancenter.org/our-work/analysis-opinion/hand-counting-votes-proven-bad-idea.
11
Этим математиком был Рене Декарт. См. David Wells, The Penguin Dictionary of Curious and Interesting Numbers (London: Penguin, 1997).
12
Этого одноклассника звали Уильям Коллинз. Кстати, его лекция на конференции TED, набравшая более 1,5 млн просмотров, называется «Как навыки видеоигр могут помочь в жизни». “How Video Game Skills Can Get You Ahead in Life.” Posted March 2021, https://www.ted.com/talks/william_collis _how_video_game_skills_can_get_you_ahead_in_life.
13
Перевод В. А. Азова и Т. Л. Щепкиной-Куперник. – Прим. пер.
14
Lewis Carroll, Through the Looking Glass (1871), Project Gutenberg, https://www.gutenberg.org/files/12/12-h/12-h.htm.
15
Charalampos Lemonidis and Anastasios Gkolfos, “Number Line in the History and the Education of Mathematics,” Inovacije UNastavi 33 (March 2020): 36–56, 10.5937/inovacije2001036L.
16
Wells, Penguin Dictionary of Curious and Interesting Numbers.
17
Там же.
18
J. J. O’Connor and E. F. Robertson, “Frances Maseres,” MacTutor History of Mathematics Archive, accessed May 15, 2023, last updated 2004, https://mathshistory.st-andrews.ac.uk/Biographies/Maseres/.




