Функционально-активные контактные материалы и системы: Теория и инновационные применения в энергетике и электронике

VAB(t) = ΦB(t) − ΦA(t) e + dVfluct(t),

Где:

dVfluct(t) – вклад флуктуаций, зависящий от типа возмущения.

2.2.2. Модель динамической асимметрии КРП.

Динамическая асимметрия КРП возникает из-за временных изменений работы выхода под воздействием флуктуаций. Рассмотрим систему из двух 1 металлов с контактной границей, подверженной тепловым флуктуациям. Температурные колебания вызывают локальные изменения концентрации носителей заряда и уровней Ферми.

Для описания этого процесса используем уравнение Ланжевена:

dΦA(t) dt = − ΦA(t) − ΦA0 τ + ξ(t),

Где:

ΦA0 – равновесная работа выхода,

τ – время релаксации,

ξ(t) – случайная сила, моделирующая тепловые флуктуации с корреляцией:

⟨ξ(t)ξ(t1)⟩ = 2kTΓd(t – t1),

Где:

k – постоянная Больцмана,

T – температура,

Γ – коэффициент диссипации.

Ток, вызванный динамической асимметрией, можно выразить через разность потенциалов:

I(t) = VAB(t) R + Rint,

Где:

R – внешнее сопротивление,

Rint – внутреннее сопротивление контакта.

Средняя мощность, выделяемая в нагрузке, определяется как:

P = (I(t) 2 )R.

Эта модель показывает, что асимметричные барьеры на межфазной границе могут преобразовывать случайные флуктуации в направленный ток, что согласуется с исследованиями по тепловым расчётам.

2.2.3. Преобразование тепловых флуктуаций.

Преобразование тепловых флуктуаций в электрическую энергию – один из ключевых механизмов ФКА. Рассмотрим контакт двух металлов с различными термоэлектрическими коэффициентами Зеебека (SA, SB). При локальном нагреве границы раздела возникает термоэлектрическая ЭДС:

Vthermo = (SB − SA)dT,

Где:

dT – температурный градиент.

В системах ФКА dT может быть вызван тепловыми флуктуациями, а не внешним источником. Для оценки тока используем модель переноса заряда через асимметричный барьер:

I = q kT интеграл J(E)f(E, T)A(E) dE,

Где:

J(E) – спектральная плотность тока,

f(E, T) – функция распределения Ферми-Дирака,

A(E) – коэффициент пропускания барьера, зависящий от его асимметрии.

Для количественной оценки эффективности преобразования рассмотрим энергетический баланс.

Входная энергия тепловых флуктуаций определяется как:

Qfluct = kT * df, 2

Где:

df – полоса частот флуктуаций.

КПД преобразования:

η = Pout Qfluct = (I 2)R kT * df .

Эта модель подтверждает, что преобразование возможно только при наличии асимметричных барьеров и неравновесных условий, что согласуется со вторым началом термодинамики.

2.2.4. Емкостная термоэлектрическая батарея.

Емкостная термоэлектрическая батарея (раздел 5.7) комбинирует термоэлектрический эффект с накоплением заряда. Рассмотрим систему из N металлических термопар, соединённых с конденсатором емкостью C. Термоэлектрическая ЭДС каждой пары:

Vi = (SB,i − SA,i)dTi .

Общая ЭДС системы:

Vtotal = сумма N i=1 Vi .

Заряд, накопленный на конденсаторе:

Q = CVtotal

а энергия:

E = 1 2 CV 2 total.

КПД системы определяется как: η = E Qin ,

Где:

Qin – входная тепловая энергия.

Для металлических термопар (S = 1−10 µV/K) и dT = 1−10 K выходная мощность ограничена, но использование емкостных накопителей позволяет интегрировать энергию во времени, повышая эффективность.

2.2.5. Соответствие законам термодинамики.

Критика ФКА часто связана с возможным нарушением закона Вольта и второго начала термодинамики. Однако предложенные механизмы не противоречат этим законам, так как:

1. Генерация ЭДС происходит за счет неравновесных состояний, вызванных внешними или внутренними флуктуациями, а не в равновесной системе.

2. Преобразование флуктуаций требует асимметричных барьеров, что соответствует принципу расчёта и не нарушает энтропийный баланс.

3. Энергия, преобразованная в электрическую, извлекается из окружающей среды (тепловые, механические или электромагнитные поля), что согласуется с первым началом термодинамики.

Для строгого доказательства рассмотрим энтропийный баланс. Изменение энтропии системы: dS = Qfluct T − Pout Teff ,

Где:

Teff – эффективная температура нагрузки.

При n < 1 энтропия возрастает, что удовлетворяет второму началу.

2.2.6 Выводы.

Предложенные модели демонстрируют, что ФКА основана на использовании неравновесных процессов и асимметричных барьеров для преобразования флуктуаций в полезную энергию. Математическое описание динамической асимметрии КРП, термоэлектрических эффектов и емкостного накопления энергии подтверждает физическую реализуемость предложенных механизмов. Эти модели требуют дальнейшей экспериментальной верификации, но они обеспечивают прочную основу для понимания ФКА в рамках классической физики.

Глава 3. Функционально – активные контактные материалы и системы

В предыдущих разделах мы заложили теоретические основы концепции функциональной контактной активности (ФКА), представляющей собой принципиально новый взгляд на электропроводящие материалы как на активные и интеллектуальные компоненты, способные к самогенерации энергии и адаптации. Глава 3 посвящена детальному рассмотрению практической реализации этих идей – функционально-активным контактным материалам и системам, которые воплощают принципы ФКА.

Здесь будут подробно изучены две основные категории таких систем: металлические проводники с функциональной контактной активностью и гибридные системы с функциональной контактной активностью. Мы разберем их уникальные свойства, механизмы работы, основанные на динамической асимметрии множества контактных разностей потенциалов, а также их способность преобразовывать различные виды внешних флуктуаций в полезную электрическую энергию. Кроме того, в главе будут представлены способы управления функциональной контактной активностью, что открывает широкие перспективы для создания инновационных, энергоэффективных и автономных устройств и систем в различных областях науки и техники.

3.1. Металлический проводник с функциональной контактной активностью

Проводник с последовательной знакопеременной контактной разностью потенциалов – это инновационное техническое решение, состоящее из последовательно соединенных сегментов разнородных металлов, см. Рис. 1.

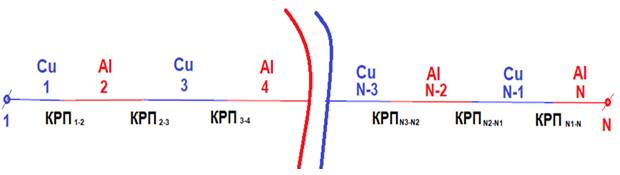
Рис. 1. Схема проводника с знакопеременной контактной разностью потенциалов.

Работа проводника основывается на уникальных свойствах переходов между разнородными металлами, которые в такой структуре становятся чувствительными к внешним воздействиям, таким как тепло, электромагнитные и электростатические поля.

Вариант исполнения проводника с последовательной знакопеременной контактной разностью потенциалов представлено на следующем Рис.унке.

Рис. 2. Проводник с знакопеременной контактной разностью потенциалов.

Механизм работы

Работа проводника с последовательной знакопеременной контактной разностью потенциалов основывается на сложных взаимодействиях, внутри переходов между разнородными материалами и между такими переходами, которые перераспределением потенциалов откликаются на внешние температурные, электромагнитные или электростатические поля. В таком проводнике проявляются следующие интереснейшие свойства:

Проводник без внешнего теплового воздействия проявляет термоэлектрические эффекты благодаря внутреннему перераспределению тока и местным изменениям температуры. Это позволяет системе адаптивно собирать естественный тепловой шум и использовать его для генерации напряжения.

Контур из такого проводника при взаимодействии с электромагнитными полями увеличивает выходное напряжение на величину, зависящую от перераспределения токов между переходами разнородных материалов.

Замкнутый контур такого проводника проявляет небольшой градиент напряжений и температур в замкнутой структуре проводника. Это противоречит классической теории, которая предполагает нулевую ЭДС в замкнутом контуре, и подтверждает, что в системе происходит стохастическое перераспределение микроскопических тепловых флуктуаций.

Взаимодействие с электростатическими полями приводит к перераспределению потенциалов меду переходами, что проявляется в наведении дополнительной ЭДС на границах контактов различных металлов.

Большое количество точек с контактной разностью потенциалов на единице длинны проводника позволяет определять место изменения термодинамического равновесия на поверхности или в объёме. Для этого в проводник подают электрический импульс с известными временными и амплитудными характеристиками и сверяют его с выходным импульсом.

Большое количество точек с контактной разностью потенциалов на единице длинны проводника позволяет управлять небольшим локальным изменением температуры отдельных контактных разностей потенциалов на плоскости или в объёме. Для этого в проводник подают с обоих сторон электрические импульсы с определёнными фазовыми соотношениями.

Заключение.

Благодаря сложным взаимодействиям тепловых, электронных и электромагнитных процессов на границах контактов различных металлов, металлический проводник с знакопеременной контактной разностью потенциалов способен генерировать микровольты напряжения, используя не только внутренние, но и внешние энергии, что открывает новые перспективы для создания энергоэффективных устройств и систем, а также управлять или диагностировать локальными изменениями температур на плоскостях или в объёме.

3.2. Гибридные системы с функциональной контактной активностью

В предыдущем разделе мы подробно рассмотрели принципы работы и уникальные свойства металлических проводников со знакопеременной контактной разностью потенциалов, демонстрирующих способность к генерации энергии и сенсингу на основе динамических контактных явлений. Развивая эту концепцию, гибридные системы с функциональной контактной активностью представляют собой следующий шаг в эволюции ФКА-материалов. Они расширяют диапазон используемых интерфейсов, включая контакты "полупроводник – металл" и "полупроводник – полупроводник", что открывает новые возможности для управления энергетическими и сенсорными характеристиками, а также для интеграции в более сложные электронные архитектуры "Полупроводник – Металл" и "Полупроводник – Полупроводник" .

Направление "Полупроводник – Металл" фокусируется на использовании интерфейсов между полупроводниками и различными металлами для создания активных систем, способных генерировать электрическую энергию и проявлять сенсорные свойства в условиях, ранее считавшихся статическими.

Рассмотрим альтернативу последовательному соединению КРП – гексагональную топологию гибридной системы с узловыми точками КРП.

Узловые точки в гексагональной топологии функционируют как критические интерфейсы, формируя контактные разности потенциалов между тремя различными материалами. Эти точки обеспечивают множественное сопряжение, генерируя контактные потенциалы одновременно для нескольких соседних контуров (например, для шести), что является основой для функциональной активности системы.

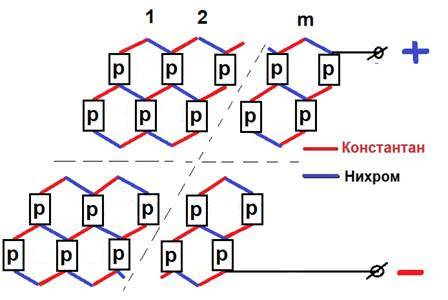
Рис. № 3. Гексагональная топология направления "полупроводник – металл"

Традиционная физика утверждает, что в условиях термодинамического равновесия сумма контактных разностей потенциалов в замкнутой цепи равна нулю (закон Вольта), и они не могут служить источником энергии. Однако, как показывает практика, материалы с функциональной контактной активностью способны обходить эти ограничения, создавая временные токовые асимметрии и генерируя устойчивую ЭДС. В полупроводниках это достигается не только за счет микроразниц температур или градиентов, но и благодаря уникальной способности их объемного заряда взаимодействовать с внешними полями.

Ключевая роль в полупроводниках с функциональной контактной активностью отводится:

1. Барьерной и диффузионной емкостям p-n перехода.

2. Переход – металл-полупроводник.

Рассмотрим эти направления подробно.

1. Барьерная и диффузионная емкости p-n перехода.

Направление "Полупроводник – Полупроводник" предполагает создание активных систем, где основными функциональными элементами являются непосредственные контакты между различными полупроводниковыми материалами, интегрированными в аналогичную гексагональную топологию.

Барьерная и диффузионная емкости p-n перехода способны накапливать электрический заряд из окружающей среды, например, от электрического поля Земли, не на обкладках, как это происходит в классическом конденсаторе, а непосредственно в объеме p-n перехода.

Воздействие внешних электрических и/или магнитных полей приводит к изменению работы выхода полупроводников и металлов на контактных границах. Это, в свою очередь, формирует динамическую, временную асимметрию в распределении зарядов и потенциалов внутри системы. Такая асимметрия позволяет создавать направленное движение электрических зарядов и генерировать ЭДС, даже когда система находится в условиях кажущегося термодинамического равновесия, без необходимости внешнего температурного градиента, как у элементов Пельтье. Таким образом, энергия извлекается из флуктуаций или постоянного внешнего поля, которое переводит систему в неравновесное состояние на микроуровне, поддерживая макроскопический ток.

2. Переход – металл-полупроводник.

Это направление исследует "непрямляющие" омические контакты между металлами (константан, нихром, медь) и полупроводниками p-типа, такими как оксид меди (CuO). В отличие от систем с p-n переходами, сам по себе полупроводник p-типа не образует барьерную или диффузионную емкость p-n перехода. Однако эксперименты показывают, что и в таких системах возникают временные токовые асимметрии под воздействием внешних электрических и магнитных полей, а также отдельных электрических зарядов.

Отмечена электростатическая аномалия, проявляющаяся в сильной зависимости выходного напряжения от местоположения наблюдателя и ориентации системы в магнитном поле Земли. В некоторых случаях наблюдались переменные компоненты выходного напряжения с частотой 0.5–1 Гц. Эти наблюдения указывают на активное взаимодействие контактной активности с окружающим электростатическим полем, что приводит к формированию асимметрий.

3.3. Способы управления функциональной контактной активности

Для полной реализации потенциала функциональной контактной активности (ФКА), особенно в приложениях, связанных с точным сенсорингом и локализованным воздействием, необходимо разработать методы адресного управления и диагностики отдельных контактных областей в сложной многоконтактной системе. Традиционные подходы часто сталкиваются с трудностями при локализации эффектов на микроскопическом уровне. Предложенный способ развертки питающего/диагностического напряжения открывает новые возможности для решения этой задачи.

Принцип работы и техническая реализация.

Схематически, способ развертки управляющего/диагностического напряжения в длинном проводнике (электрической цепи) представлен на следующем рисунке.

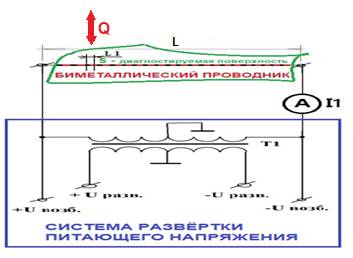
Рис. № 4. Схема реализации способа способ развертки управляющего/диагностического напряжения в длинном проводнике (электрической цепи).

Длинный проводник с знакопеременной контактной разностью потенциалов имеет

большое количество точек с контактной разностью потенциалов на единице длинны.

Большое количество точек с контактной разностью потенциалов на единице длины диагностического проводника (L) позволяет точно определять сегмент с КРП с выходом из термодинамического равновесия (нагрев или охлаждение) или наоборот, управлять нагревом или охлаждением заданных сегментов КРП.

Для сканирования каждой точки КРП в биметаллический проводник с знакопеременной контактной разностью потенциалов, с обоих сторон подают возбуждающие напряжениях противоположной полярности от выходной обмотки специального сканирующего трансформатора Т1.

Управлении фазовыми соотношениями двух возбуждающих напряжениях противоположной полярности , прикладываемые с обоих сторон проводника с КРП происходит в сканирующем трансформаторе Т1 с двумя обмотками со средними точками.

Частота возбуждающих напряжений Uвозб. противоположной полярности равной: