400 математических графиков. Школа, колледж, вуз

400 математических графиков

Школа, колледж, вуз

С. Н. Старков

© С. Н. Старков, 2025

ISBN 978-5-0067-2135-7

Создано в интеллектуальной издательской системе Ridero

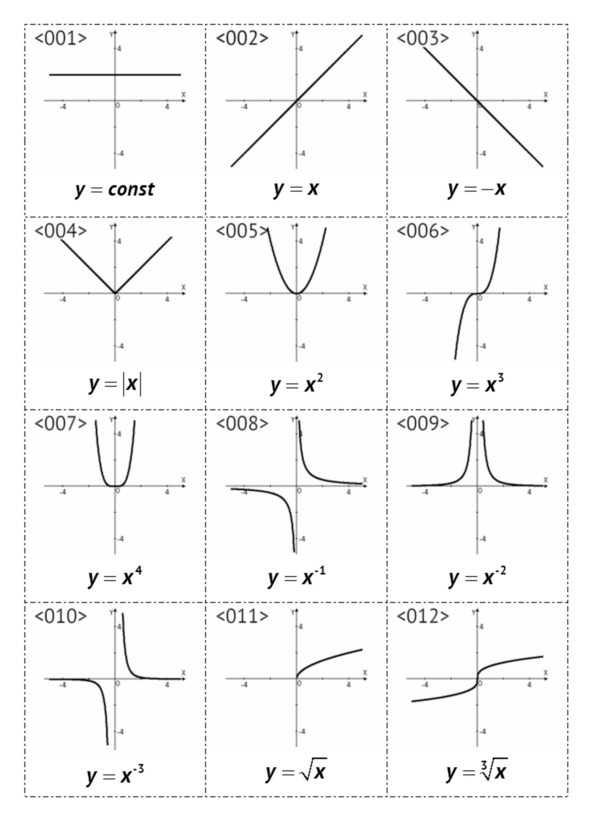
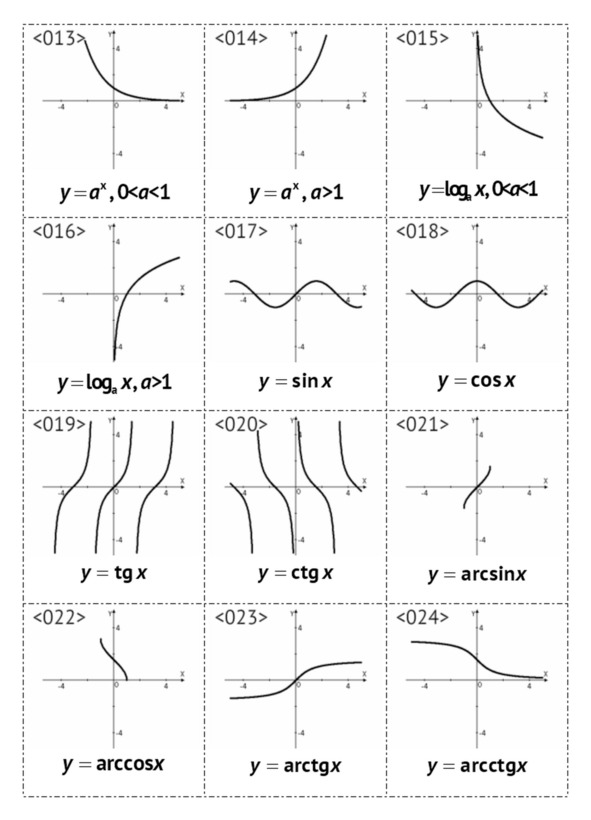
§1. Графики основных элементарных функций, <001> – <024>

В данном параграфе рассмотрены основные элементарные функции следующего вида:

– степенные y=xr,

– показательные y=ax,

– логарифмические logax,

– тригонометрические: sinx, cosx, tgx, ctgx,

– обратные тригонометрические: arcsinx, arccosx, arctgx, arcctgx.

Всего приведено 24 примера графиков.

Здесь и далее (до §8) используется

явный способ задания функций

в прямоугольной системе координат.

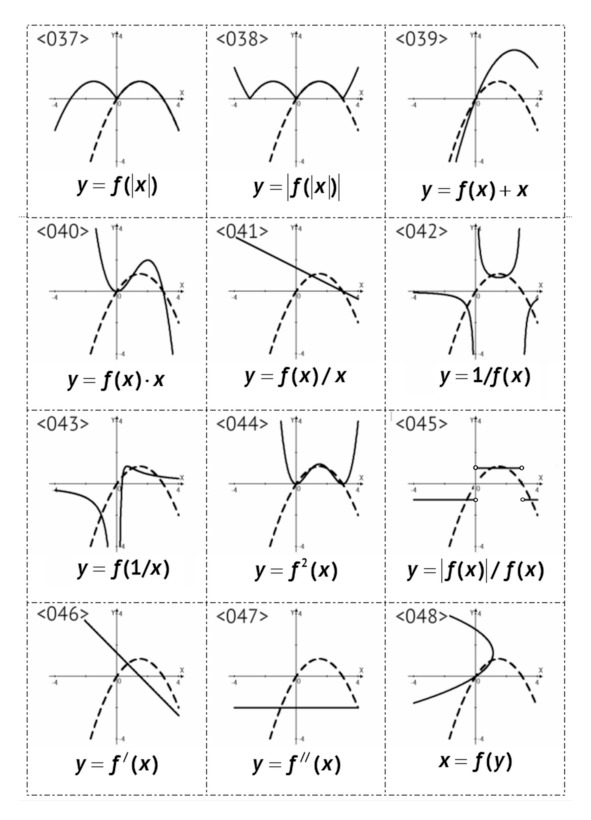
§2. Преобразования графиков, <025> – <048>

В данном параграфе рассмотрены преобразования графиков следующих типов:

– параллельный перенос: y=f (x+a), y=f (x) +a;

– растяжение и сжатие: y=f (kx), y=kf (x);

– симметричное отражение: y=f (-x), y=-f (x);

– инверсия: y=1/f (x), y=f (1/x);

– сложение y=f (x) +g (x);

– умножение y=f (x) g (x);

– деление y=f (x) /g (x);

– суперпозиция y=f (g (x)).

Всего приведено 24 примера преобразований.

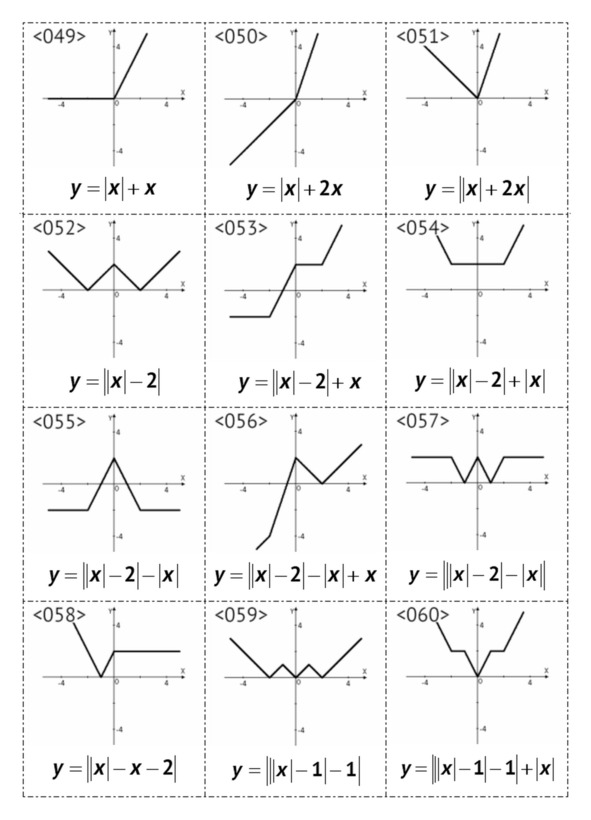
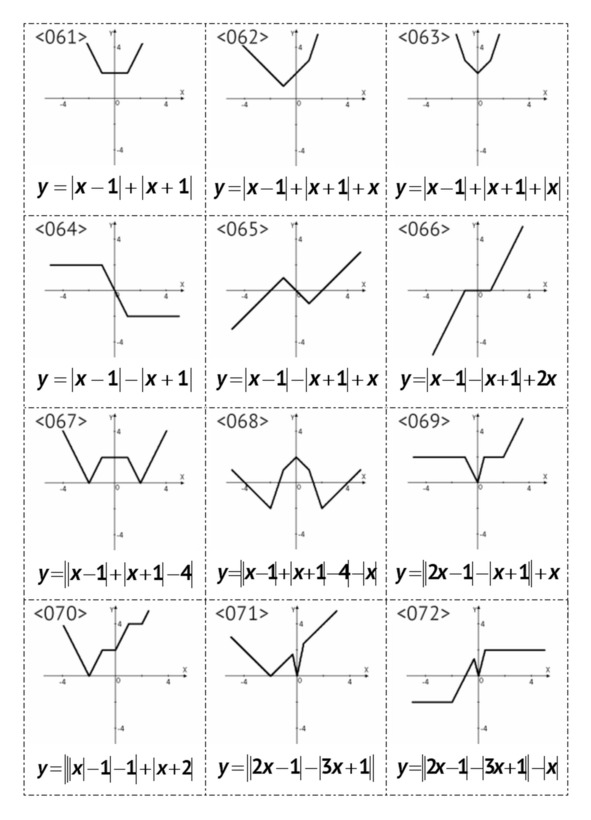
§3. Графики линейных функций, <049> – <072>

В данном параграфе рассмотрены линейные и кусочно-линейные графики функций, содержащих знак модуля.

Линейные функции и графики находят широкое применение для точного и приближенного моделирования явлений. Их применяют при решении задач:

– аппроксимации,

– интерполяции,

– экстраполяции,

– оптимизации.

§4. Графики многочленов различных степеней, <073> – <096>

В данном параграфе рассмотрены графики многочленов 2-й, 3-й, 4-й, 5-й и 6-й степени.

В общем виде многочлен n-й степени от одной переменной может быть задан формулой

y=Pn (x) = a0xn+a1xn-1+a2xn-2+ … +an-1x+an.

Известно, что многочлен может иметь не более n действительных корней. Если многочлен имеет m действительных корней xi кратности mk, то он может быть представлен в виде разложения на множители:

y=Pn (x) =a0 (x-x1) m1 … (x-xm) mk (x2+px+q) l1 … (x2+rx+s) lr,

где квадратичные множители не имеют действительных корней. В такой форме можно увидеть точки пересечении графика с осью OX и примерный эскиз графика в окрестностях этих точек.