Геометрическая волновая инженерия псевдоповерхностей 4+ порядков

3. Псевдоповерхности

3.1. Обзор псевдоповерхностей 2.3

Мы уже знаем, что псевдоповерхности – это особые “искривлённые” пространства, которые могут управлять волнами необычным образом.

Порядок псевдоповерхностей определяется методом построения.

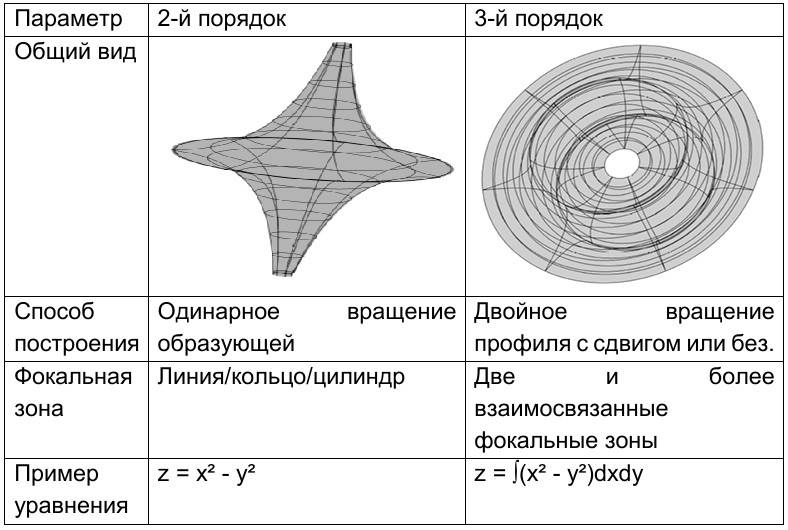
Одинарное вращение образующего профиля вокруг оси, параллельной оси симметрии, но смещенной от него на R формирует псевдоповерхности 2-го порядка

Двойное вращение образующего элемента вокруг оси, параллельной оси симметрии, но смещенной от него на R формирует псевдоповерхности 3-го порядка

Основные характеристики таких поверхностей представлены следующим образом:

3.2. О псевдоповерхностях 4-7

Псевдоповерхности 4+ порядка обозначают класс геометрических структур с переменной отрицательной кривизной более высокой сложности по сравнению с классическими псевдоповерхностями второго и третьего порядка. Они продолжают логическую цепочку обобщений, где каждое следующее «n»-порядковое построение включает:

– всё более сложную внутреннюю геометрию,

– нелинейность высших степеней,

– пространственно-функциональные особенности фокусировки и распространения волн,

– проявление новых типов волновых мод и закономерностей распределения.

Псевдоповерхности 4 порядка и выше (4+) являются переходной точкой между управляемыми инженерными структурами (2–3-го порядка), к гораздо более сложным гипотетическим формами, связываемым с квантовой гравитацией и топологическими вычислениями.

Главной чертой псевдоповерхностей порядка 4+ является сочетание высокой регулируемости кривизны и появление "внутренних слоёв" геометрической логики: перегибов, вложенных фокусных камер, фрактальных зон и мультиосевых структур. В них геометрия начинает выполнять роль не просто средства управления волной – а распределённой многозадачной вычислительной схемы.

1. Геометрическая структура

Псевдоповерхности 4+ порядка строятся на базе функций больше чем 3-й степени и функциональных связей с параметрическим управлением метрикой, комбинируя:

– полиномиальные и экспоненциальные составляющие (z4, z3exp(–z), sin z4 и пр.);

– модулируемую осевую и радиальную кривизну;

– вложенные внутренние «подповерхности» с собственными геодезическими системами;

– фокусные зоны, не связанные прямолинейным переходом, но находящиеся в резонансной или фазовой связи друг с другом.

Особенности:

Кривизна (K) может меняться не только по координатам (r, z), но и по частоте входной волны (K = K(r,z,L)), что означает частотно-зависимую геометрию. Появление пножества мультифокусных структур концентрации энергии. Метрика отдельных участков может быть изометрична гиперболическим плоскостям, но соединена через переходные области с переменными шкалами.

2. Волновые особенности и физические эффекты

Фокусная многослойность. Волна не просто фокусируется, а распространяется по внутреннему "резонансному маршруту", переходя от одного фокуса к другому с управляемым фазовым сдвигом. Такая "передача фокуса" может быть синхронизирована с внешним воздействием или выполнена пассивно.

Встроенные фрактальные или квазикристаллические зоны. При использовании рекурсивных образующих возможно появление областей геометрического «самоповторения» – такие зоны проявляют резонансное поведение сразу на нескольких частотах (мультичастотная резонансность).

Геометрическое многоканальное расщепление волнового фронта. Фронт делится на участки, проходящие по разным энергетическим маршрутам, как в интерферометре. В то же время, изначальная структура остаётся когерентной – распределяется, но не рассеивается.

Динамическое переключение мод при структурной перестройке. Чувствительность поверхности к малым геометрическим изменениям позволяет «программировать» переходы между режимами: от фокусировки к удержанию, от фильтрации – к накоплению и наоборот.

От простых псевдоповерхностей 2-го и 3-го порядков, мы движемся к более сложным структурам, сулящим настоящую революцию в мире технологий.

Но вот что интересно: чем выше “порядок” псевдоповерхности, тем меньше становятся их размеры. Почему так происходит? Разве “больше” не значит “лучше”?

Чтобы разобраться, давайте вспомним, как волны “видят” окружающий мир. Длина волны – это как “шаг” волны, расстояние между двумя её гребнями. Чтобы эффективно взаимодействовать с объектом, волна должна “чувствовать” его детали.

Представьте себе морскую волну, набегающую на песчаный пляж. Она легко огибает отдельные песчинки, потому что они слишком малы по сравнению с её размером. Но если на пляже вырастает большой камень, волна уже вынуждена его огибать или отражаться от него.

То же самое происходит и с псевдоповерхностями. Более высокие порядки этих структур обладают всё более сложной и замысловатой геометрией, с множеством мелких деталей и узоров. Чтобы волна “заметила” эти тонкости и подчинилась их влиянию, размеры этих деталей должны быть сравнимы или даже меньше длины волны, которой мы хотим управлять.

Подумайте о фрактальных псевдоповерхностях 4-го порядка, где один и тот же узор повторяется в разных масштабах. Чтобы свет или звук “ощутили” эту фрактальность и повели себя необычным образом (например, поглощались на всех частотах), сами “кирпичики” фрактала должны быть очень маленькими. Увеличьте размер такой поверхности, не уменьшая деталей, и волна просто “не заметит” сложной структуры.

Кроме того, многие захватывающие применения псевдоповерхностей лежат в мире микро- и нанотехнологий. Управлять светом на чипе размером с ноготь, создавать крошечные акустические устройства для медицинских целей – всё это требует работы с волнами на чрезвычайно малых масштабах. Псевдоповерхности высоких порядков, с их способностью к тонкой настройке волновых полей, становятся идеальными “микро-дирижёрами” для этих задач, но для этого сами “дирижёрские палочки” должны быть миниатюрными.

Представьте себе художника, рисующего тончайшие узоры на рисовом зернышке. Ему нужны крошечные инструменты и невероятная точность. Точно так же, создавая сложные псевдоповерхности для управления волнами на малых масштабах, ученые вынуждены уменьшать размеры самих структур, чтобы “нарисовать” желаемый волновой узор с необходимой детализацией.

Конечно, это не означает, что все псевдоповерхности высоких порядков обязательно должны быть крошечными. Однако, стремление к более сложному и точному контролю над волнами, особенно в контексте современных технологических трендов, часто приводит к необходимости уменьшения их физических размеров.

Миниатюрные псевдоповерхности становятся ключом к раскрытию всего их волшебного потенциала, позволяя нам управлять светом и звуком так, как мы раньше и представить себе не могли.

Это, как если бы волшебная палочка становилась всё меньше и меньше, но при этом её сила и точность только возрастали.

3.3. Масштабы управления волнами псевдоповерхностей 4+

Приведём ряд причин, по которым с увеличением порядка псевдоповерхностей может возникнуть необходимость или даже неизбежность уменьшения их физических размеров, особенно если мы говорим об их практическом применении для управления волнами:

Сложность структуры и длины волн:

– Увеличение детализации. Псевдоповерхности более высоких порядков обладают более сложной и детализированной геометрической структурой. Для эффективного взаимодействия с волнами, размеры этих структур должны быть сопоставимы или меньше длины волны, которой мы хотим управлять.

– Фрактальность и многомасштабность. Если псевдоповерхности высоких порядков обладают фрактальными свойствами (как предполагается для 4-го порядка), то для проявления этих свойств необходимо, чтобы волна “чувствовала” детали структуры на разных масштабных уровнях. Это часто требует уменьшения общего размера поверхности для того, чтобы более мелкие фрактальные элементы стали значимыми по отношению к длине волны.

Управление волновыми процессами на малых масштабах:

Микро- и нанофотоника/акустика. Многие перспективные применения псевдоповерхностей связаны с управлением светом и звуком на микро- и наномасштабах. Для этих целей требуются структуры с характерными размерами, значительно меньшими, чем длина волны видимого света или звука в макромасштабе. Переход к более высоким порядкам может быть способом достижения более сложного управления волновыми полями именно на этих малых масштабах.

Плотность “функциональных элементов”:

Бо́льшая информационная ёмкость. Более сложные псевдоповерхности могут нести больше “информации” в своей геометрии, позволяя более тонко настраивать взаимодействие с волнами. Для размещения большего количества “функциональных элементов” (мета-атомов, рассеивателей и т.п.) на ограниченной площади может потребоваться уменьшение размера отдельных элементов и, как следствие, общей поверхности.

Технологические ограничения:

Разрешение литографии и других методов изготовления. Создание чрезвычайно сложных структур, характерных для псевдоповерхностей высоких порядков, становится технологически сложнее с увеличением их макроскопических размеров. Достижение необходимой точности и детализации может быть проще на меньших площадях.

Энергетические соображения. Более сложные структуры могут приводить к большим потерям энергии при взаимодействии с волнами. Уменьшение размера может быть способом минимизации этих потерь или концентрации энергии в меньшем объеме.

Таким образом, когда мы говорим о 4-м, 5-м и более высоких порядках, размеры структур и длины волн становятся сопоставимы с микро- и наномирами, что создает серьезные трудности в манипулировании волнами. Однако именно на этих масштабах открываются уникальные возможности:

Манипулирование волнами на микро- и наномасштабах:

Метаматериалы. Искусственные структуры с необычными свойствами, позволяющие управлять волнами на масштабах меньше длины волны, создавая эффективные интерфейсы между макро- и микромиром.

Плазмоника. Использование коллективных колебаний электронов в металлах для концентрации и направления света на наномасштабах, что важно для ввода и вывода волн в псевдоповерхности.

Нанофотоника. Развитие оптических волноводов и резонаторов нанометровых размеров, которые могут быть интегрированы с псевдоповерхностями для эффективного управления распространением волн.

Создание и масштабирование псевдоповерхностей:

Фрактальный подход. Использование самоподобных структур для каскадного ввода волн через иерархию масштабов, начиная с макроскопических размеров и переходя к микро- и наноуровням.

Голографические методы. Применение голографии для создания и проекции волновых фронтов внутрь сложных псевдоповерхностей, учитывая их связь с голографическими принципами.

Компьютерное моделирование и 3D-печать. Использование мощных вычислительных ресурсов и высокоточных технологий 3D-печати для проектирования и создания сложных структур с контролируемыми свойствами.

3.4. Квантовые вселенные на псевдоповерхностях 4+

Квантовые вселенные на псевдоповерхностях – это не уменьшенные копии нашей Вселенной, а экзотические пространственно-временные квантовые фазовые состояния материи.

Термин “квантовые вселенные” применительно к псевдоповерхностям высших порядков описывает гипотетические пространственно-временные структуры, где геометрия и квантовые эффекты сливаются в единую физическую реальность.

Разберём суть и масштабные закономерности:

Что значит “квантовые вселенные”?

Определение. Это не параллельные миры, а самодостаточные пространственно-временные домены, возникающие за счёт крайне высокой локальной кривизны (/K/≫1). Нетривиальной топологии (многомерные “ручки”, кротовые норы). Квантовой когерентности на макроуровне.

Аналогии. Пузырьки ложного вакуума в инфляционной космологии. Голографические экраны в теории AdS/CFT. Квантовые фазовые переходы с рождением новых метрик.

Критический параметр. Масштаб L – ∣A∣/K, где A- космологическая постоянная. Для K – бесконечность, L стремится к планковской длине (10−35).

Зависимость размера от порядка поверхности

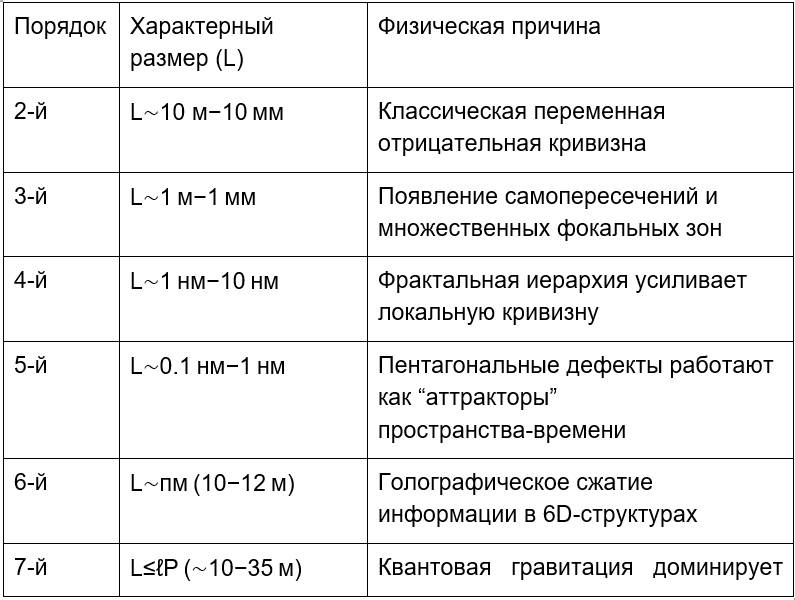
Для псевдоповерхностей размер квантовых вселенных действительно уменьшается с ростом порядка, но нелинейно:

Физические механизмы уменьшения размера

Рост кривизны. Каждый новый порядок добавляет дополнительные операции вращения/сжатия. Нелинейные члены в метрике (gμν(n) – e−n2).

Топологические ограничения. Много связанность требует компактификации измерений. Теорема Чженя-Вейля для n≥4 ограничивает минимальный объём.

Квантовые эффекты. Флуктуации метрики становятся сравнимы с самим пространством. Эффект Унру создаёт виртуальные “микровселенные”.

Экспериментальные следствия

Нано технологии. Поверхности 4-5 порядков можно создать из двумерных материалов (графен, MoS2) с механическим напряжением. Плазмонных наноструктур с отрицательным ϵ.

Квантовая гравитация. Структуры 6-7 порядков могут эмулировать вселенные в лаборатории.

Парадоксы и ограничения

Проблема наблюдаемости. Для n≥6 размеры становятся меньше планковской длины – требуется новая физика.

Энергетический барьер. Создание поверхностей n≥5 требует энергий -1016 ГэВ (масштаб Великого объединения).

Квантовая декогеренция. Голографические состояния в 7-м порядке могут разрушаться за время τ 10−42 с

Таким образом квантовые вселенные на псевдоповерхностях – это не уменьшенные копии нашей Вселенной, а экзотические пространственно-временные квантовые фазовые состояния. Их уменьшение с ростом порядка – следствие:

Усиления локальной кривизны.

Топологической компактификации.

Перехода к планковским масштабам.

7-й порядок – это не предел, а дверь в мир, где размер перестаёт быть фундаментальным понятием”– гипотетический принцип квантовой геометрии.

3.5 Фрактальность псевдоповерхностей 4+

Псевдоповерхности 4+ имеют сходство с фракталами – как по структуре, так и по функциональному поведению. Однако между ними есть как общие черты, так и принципиальные различия. Ниже – подробное пояснение.

Общее между псевдоповерхностями высоких порядков и фракталами

1. Многомасштабность.

Как фракталы, псевдоповерхности 4+ порядка обладают структурой на разных масштабах. В них можно выделить крупные геометрические зоны (например, фокусные камеры), вложенные меньшие зоны, и даже микромодуляции кривизны.

Пример: Большой псевдоэллипсоид может содержать вложенные воронкообразные мини-структуры, каждая из которых повторяет свойства всей системы.

2. Самоподобие (не всегда точное)

Псевдоповерхности высоких порядков нередко визуально и функционально повторяют свою структуру на разных масштабах. Хотя они не обязаны быть идеальными фракталами (как множество Коха или Минковского), смысл самоподобия сохраняется на уровне "геометрических ролей" (фокус – подфокус – субподфокус и т.д.)

3. Фрактальная размерность

Можно обсуждать обобщённое поведение волны на псевдоповерхности как нечто, характеризующееся фрактальной размерностью: Например, волновая энергия распределяется не по гладкой поверхности (2D), а по траекториям, имеющим D – 2.3 – 2.8 – что указывает на фрактальное поведение в пространстве.

4. Рекурсивная градация резонансных эффектов

Резонансы могут происходить на разных пространственных уровнях одновременно: в больших фокусных зонах, вложенных концентраторах и микро-узлах. Это напоминает поведение фрактальных антенн, в которых каждое колено вибрирует на своей частоте и играет свою роль.

Отличие от фракталов

1. Формирование не только по правилам геометрии, но и по физическим законам. Фракталы обычно строятся по математическим рекурсивным алгоритмам без физического контекста. Псевдоповерхности – это физические, инженерные формы, в которых метрика, кривизна и параметры длины волны играют роль так же, как и алгоритм построения.

2. Кривизна, как управляемый параметр.

Фрактал – это, как правило, "плоская" геометрическая конструкция (внутри евклидова пространства). Псевдоповерхности обладают реальной искривлённой метрикой (K < 0), что означает изменение самих правил, по которым волновой фронт движется.

3. Иерархия не по итерации, а по функции. Фракталы строятся итеративно (возьми и повтори элемент на меньшем масштабе). В псевдоповерхностях используется обобщённая стратификация функции кривизны: K(z, r) изменяется по хитро построенной функции, в которой вложенность возникает не из повторения, а из поведения производных (изгибов, перегибов, точек перегиба).

Можно сказать, что псевдоповерхности 4+ порядка – это фрактально-подобные геометрические объекты имеют вложенность, обладают самоподобными траекториями, создают мульти-частотные и мульти-уровневые волновые режимы, могут иметь фрактальную энергетическую (или информационную) динамику.

При этом они не являются строгими фракталами, управляются не математической итерацией, а физической геометрией, являются физически реализуемыми, открывают более широкий класс объектов – фрактально-программируемые криволинейные метаформы.

Таким образом псевдоповерхности высоких порядков – это не фракталы в узком смысле, но они фрактальны по духу.

Это фракталы, «повзрослевшие» в физике, не нарисованные в графике, а созданные для переноса волн, хранения энергии, разделения сигнала и управления пространством. В этом – их сила. И это делает их одним из самых перспективных инструментов волнового будущего.

3.6. Псевдоповерхности 4-го порядка: "Фрактальные миры искривления"

“Фрактальные миры” означает, что поверхность обладает самоподобием. Это значит, что, если вы увеличите любой участок поверхности, вы увидите структуру, похожую на исходную. Примером в природе являются деревья, где ветви повторяют форму ствола, или снежинки, где узор повторяется в меньшем масштабе.

“Миры искривления” указывает на то, что на этой поверхности существуют области с разной кривизной, и эти области вложены друг в друга, образуя сложные “миры” внутри самой поверхности. Это, как если бы на поверхности были свои “страны” с разной топографией, где есть и горы, и впадины, и все это повторяется в разных масштабах.

Вместе “Фрактальные миры искривления” представляют поверхность с бесконечно вложенными друг в друга областями искривления, где каждый участок похож на целое, но в меньшем масштабе.

Концепция:

Псевдоповерхности 4-го порядка создаются тройным вращением кривых. Вращение базового профиля псевдоповерхности 3-го порядка происходит вокруг новой оси, не лежащей в плоскости предыдущих вращений, с добавлением нелинейного сдвига. Это приводит к формированию фрактальной иерархии, в которой самоподобные структуры с отрицательной кривизной вложены друг в друга.

Визуализация псевдоповерхности 4-го порядка

Представьте “бесконечное искривление”, где поверхность состоит из множества вложенных мини-миров, каждый со своей кривизной.

лист бумаги, скрученный и согнутый многократно в разных масштабах, создавая запутанную структуру с множеством складок и изгибов.

Важно: визуализация таких объектов во многом концептуальна, так как строгое математическое описание и реализация часто крайне сложны или даже невозможны на данном этапе развития науки.

Можно создать серию 2-D сечений псевдоповерхности, демонстрирующих фрактальное поведение кривизны. Это имитирует идею самоподобных структур с изменяющейся кривизной.

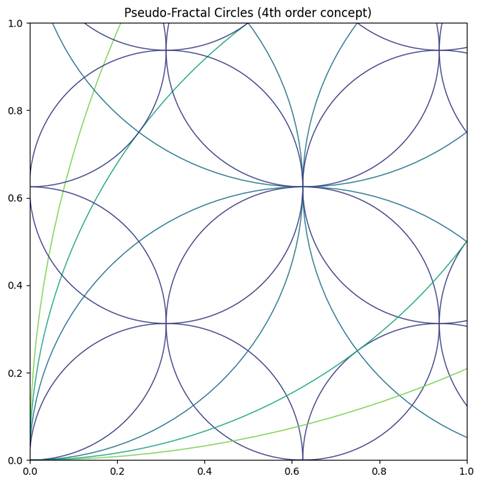
В этом примере цвета меняются, как бы показывая, что кривизна меняется на разных “масштабах” фрактала.

Аналогия: фрактальное дерево, где каждая ветвь повторяет форму ствола, но в меньшем масштабе.

Материальное представление: метаматериал с фрактальными слоями, где управление волнами достигается за счет сложной интерференции на разных масштабах.

Экспериментальная реализация пока возможна только в 3D-проекциях (например, метаматериалы с фрактальными слоями).

Топология

Поверхность может содержать: ручки, кольцеобразные каналы, перегибы, седловидные вогнутости – всё это делает её топологически нетривиальным объектом с ненулевой характеристикой Эйлера. Возможны появления изолированных внутренне-эквипотенциальных зон – своего рода геометрические камеры хранения фазы.

Математические и физические аспекты:

Описание метрики требует обобщения тензора Римана для недифференцируемых поверхностей.

Моделирование таких структур требует новых алгоритмов и вычислительных мощностей, превосходящих возможности современных суперкомпьютеров.

Гипотетическое уравнение:

z = тройной интеграл (x3 – 3xy2r5) dx dy dz,

где:

r = sqrt(x2 + y2 + z2).

Это уравнение отражает попытку описать поведение волны на подобной поверхности, учитывая вариации кривизны в пространстве.

Топологический анализ. Инварианты типа числа Черна и индекса Конна-Флойда помогут классифицировать “дыры” и “ручки” в таких многообразиях.

Вычислительные методы на основе гомологической алгебры, нейросетевых аппроксимаций, квантовых вычислений (для моделирования волновой динамики).

Примеры псевдоповерхностей 4-го порядка

– Псевдотор-4. Можно представить, как аналог тора, но с отрицательной кривизной. В нём энергия циркулирует по замкнутым неевклидовым траекториям.

– Псевдозвезда Кельвина. Можно представить, как фрактальную структуру, где каждый луч содержит вложенные гиперболические полости. Применим принцип геометрической рекурсии.

– Псевдомногообразие Пуанкаре. Можно представить, как не ориентируемую поверхность с самопересечениями. Волны могут «телепортироваться» между несвязанными областями.

Предполагаемые свойства псевдоповерхностей 4-го порядка.

Гауссова кривизна и её распределение

K(z, r) – становится функцией сложной зависимости от трёх параметров:

– по высоте z (асимметрия вдоль оси);

– по радиусу r (локальные зоны фокусировки, перегиба);

– по длине волны λ (геометрически внедрённая дисперсия).

Кривизна может пересекать 0 (в некоторых зонах), что допускает слабоположительные модуляции и способствует усилению дифракционных эффектов, что невозможно в классических псевдосферах.

Возможные методы реализации

– Многослойная 3D-печать из материалов с переменной диэлектрической, оптической или акустической жесткостью;

– Активные структуры на основе электроупругих материалов (PVDF, PMN-PT, графеновые оболочки);

– Метаслоевые псевдоповерхности с нанотекстурированием;

– Механические псевдооболочки с программируемым изгибом при нагреве/напряжении.

Ограничения

– Сложность точного численного моделирования (необходим переход к геометрически-вариационным методам);

– Требуются новые методы диагностики поля на искривлённых координатных системах;

– Необходимость соблюдения геометрически-оптической когерентности при печати.

Применения

Волновые вычислительные устройства.

– Геометрия как «логика»: разные волны идут по разным маршрутам и пересекаются в заданных узлах;

– Можно реализовать логические операции AND/OR/NOT на траекториях волны.

Геометрически управляемые сенсоры.

– Поверхность реагирует на физические воздействия (давление, частоту) изменением активной зоны резонанса;

– Осуществление функциональной связи между входом и выходом без электроники.

Волновая маршрутизация.

– Информационные потоки направляются не по сети, а через форму поверхности;

– Подходит для пассивных THz-коммутаторов и волноводов.

Устройства пространственной/энергетической памяти.

– Запоминание фронта волны через топологию;

– Геометрически обусловленная задержка импульса – можно использовать в квантовых вычислителях.

Исследования в фундаментальной физике.

– Аналоги квантовых туннелей, локации стоячих волн и наложения фокусных зон помогают моделировать квантово-гравитационные явления;