Геометрическая волновая инженерия псевдоповерхностей 2-го и 3-го порядков

3. Псевдоповерхности с отрицательной кривизной 2-го порядка

3.1. Обзор известных псевдоповерхностей с отрицательной кривизной и их междисциплинарное значение

Представьте себе математиков XIX века, таких как Лобачевский и Бойяи, которые смело вышли за рамки привычной евклидовой геометрии, создавая целые новые миры в своем воображении, где параллельные прямые могли расходиться. Их работы по неевклидовой геометрии поначалу казались чистой абстракцией, игрой разума. Однако появление псевдосферы Бельтрами стало своего рода триумфом этих идей, продемонстрировав, что такие "странные" геометрии могут существовать и в нашем, пусть и искривленном, трехмерном мире. Псевдосфера стала первым конкретным примером поверхности, обладающей свойствами неевклидовой плоскости, связав абстрактную математику с потенциальной физической реальностью.

Понятие кривизны поверхности является фундаментальным в дифференциальной геометрии, описывая степень отклонения поверхности от плоскости. Кривизна может быть положительной, как у сферы, нулевой, как у плоскости или цилиндра, или отрицательной, как у седла. Поверхности с постоянной отрицательной кривизной сыграли ключевую роль в развитии неевклидовой геометрии. В частности, работы Николая Лобачевского, Яноша Бойяи и Карла Фридриха Гаусса заложили основы для понимания пространств, отличных от евклидова. Эудженио Бельтрами первым доказал непротиворечивость неевклидовой геометрии, смоделировав ее на псевдосфере. Гаусс также изучал поверхность вращения трактрисы, отмечая ее постоянную отрицательную гауссову кривизну в неопубликованных заметках.

Псевдосфера Бельтрами (2-го порядка)

Псевдосфера Бельтрами стала отправной точкой для последующих исследований, направленных на создание новых классов псевдоповерхностей, но уже с переменной отрицательной кривизной. Таких как псевдопараболоид, псевдогиперболоид и псевдоэллипсоид.

Фундаментальная псевдосфера Бельтрами с постоянной отрицательной кривизной

Псевдосфера определяется как поверхность с постоянной отрицательной гауссовой кривизной, что противоположно сфере, имеющей положительную кривизну. Величина постоянной отрицательной гауссовой кривизны составляет K = -1/R2,

где R – псевдорадиус поверхности.

Псевдосфера образуется вращением трактрисы, также известной как трактоида или эквитангенциальная кривая. Трактриса представляет собой путь объекта, который тянут за нить постоянной длины по прямой горизонтальной линии, причем нить всегда остается касательной к траектории.

Существует несколько параметрических уравнений трактрисы, в зависимости от выбранной параметризации:

– с использованием параметра t: x(t) = a (t – tanht), y(t) = a secht.

– с использованием угла Q: x = a(ln[tan(Q/2)] + cosQ), y = a sinQ.

– с использованием обратной функции Гудермана gd-1Q: x = a gd-1Q – sinQ, y = a cosQ.

другие формы, включающие гиперболические функции и логарифмы.

Дифференциальное уравнение трактрисы имеет вид: dydx = − Sqrt (a2−x2)/x. Геометрия псевдосферы представляет собой поверхность вращения трактрисы вокруг ее асимптоты, причем асимптота становится осью вращения.

Первая фундаментальная форма (метрический тензор) псевдосферы может быть записана как ds2 = du2 + dv2/v2 в подходящей параметризации, или ds2 = a2 sech2(v) dv2 + a2 sech4(v) du2.

Полная кривизна (гауссова кривизна) K = -1/R2 постоянна, что определяет внутреннюю геометрию поверхности, где в каждой точке псевдосфера обладает отрицательно искривленной геометрией седла.

Важно отметить, что псевдосфера локально изометрична плоскости Лобачевского (гиперболической плоскости), что означает, что локально расстояния и углы на псевдосфере такие же, как и на гиперболической плоскости.

Визуальные представления и 3D-модели.

Характерная форма псевдосферы – это форма рога, часто изображаемая как поверхность с заострением и сингулярностью на экваторе. Существуют визуализации, демонстрирующие геодезические линии на псевдосфере, которые при отображении на модель Пуанкаре верхней полуплоскости соответствуют прямым линиям или дугам окружностей, перпендикулярным вещественной оси. Встречаются 3D-модели и скульптуры, вдохновленные псевдосферой, например, мемориал Бойяи и модели из бумаги или других материалов. Следует также отметить существование «дышащих псевдосфер» и других связанных псевдосферических поверхностей, получаемых из решений уравнения синус-Гордона, которые могут иметь более сложную и «дышащую» форму.

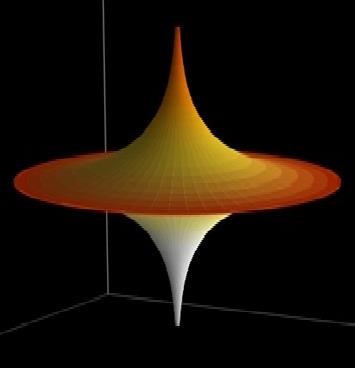
Рис. № 1. 3D-модель псевдосферы Бельтрами с постоянной отрицательной кривизной.

В псевдосфере (сферической полости) энергия концентрируется в геометрическом центре. Физически это происходит потому, что:

Механизм концентрации:

Все лучи, исходящие из центра, отражаются от стенок и возвращаются обратно в центр.

После многократных отражений возникает стоячая волна с максимумом энергии в центре.

Аналогично звуковым волнам в сферическом помещении.

Математическое обоснование:

В сферических координатах решение волнового уравнения дает максимум амплитуды при r=0.

Условие резонанса: диаметр сферы = n·L/2,

где n – целое число.

Применение в электромагнитных и акустических резонаторах

Псевдосфера обладает потенциалом для моделирования замкнутых резонаторов для электромагнитных и акустических волн, особенно благодаря своей способности удерживать энергию за счет своей геометрии. Исследования показывают поведение электромагнитных волн и частиц (например, электронов в графене) на псевдосфере Бельтрами, изучаются такие явления, как релятивистские уровни Ландау и квантовый эффект Холла в присутствии магнитных и электрических полей.

Также изучается использование графеновых листов в форме псевдосферы Бельтрами в качестве аналогов искривленных пространств-времен для обнаружения эффектов Хокинга-Унру. В акустических резонаторах псевдосферическая геометрия также демонстрирует интересные свойства, спектральное упорядочение собственных мод выявляет отрицательную кривизну, подтверждая, что звук гиперболического барабана отличается от звука евклидова барабана.

Аналогии в волновой динамике с явлениями черных дыр

Существует аналогия между волновой динамикой на псевдосфере и явлениями черных дыр, особенно в отношении «захвата» энергии из-за хаотического рассеяния, где геодезические линии ведут себя как в гиперболическом пространстве. Высокая добротность (Q-фактор) резонаторов может быть обусловлена многократными отражениями внутри искривленной структуры.

Проводится аналогия с горизонтом событий черной дыры, где энергия, попавшая внутрь псевдосферы, может с трудом покинуть ее из-за геометрии. Исследования графена в форме псевдосферы Бельтрами также проводятся как аналог черной дыры для обнаружения излучения, подобного излучению Хокинга.

3.2. Новый класс псевдоповерхностей с переменной отрицательной кривизной 2-го порядка

Одним из ключевых достижений геометрической волновой инженерии (ГВИ) стало формирование нового класса псевдоповерхностей, обладающих переменной (то есть не постоянной) отрицательной Гауссовой кривизной и аксиальной симметрией. Эти поверхности представляют собой обобщения классической псевдосферы Бельтрами и реализуются путём вращения специально сконструированного профиля вокруг оси, смещённой относительно оси симметрии. В результате формируются сложные геометрические тела, способные управлять волновым фронтом не только глобально, но и на локальных участках, что создаёт новые возможности фокусировки, направленной передачи и пространственной локализации волн.

К данному классу относятся:

– Псевдопараболоид 2-го порядка.

– Псевдогиперболоид 2-го порядка.

– Псевдоэллипсоид 2-го порядка.

Каждая из этих поверхностей сохраняет ключевые принципы нелокальной геометрии гиперболических (K < 0) структур, но дополнительно вводит асимметрию, масштабируемость и возможность вариативного управления геодезическими траекториями. Они не являются поверхностями постоянной отрицательной кривизны, как в случае идеальной псевдосферы, однако их пространственная структура тщательно спроектирована таким образом, чтобы сохранять основные гиперболические свойства с добавлением новых функциональных характеристик.

Общие геометрические и функциональные черты представителей этого класса:

– Все поверхности формируются вращением образующего профиля, представляющего собой композицию двух кривых, обеспечивающих плавное, но контролируемое изменение кривизны по высоте и радиусу.

Образующий профиль, который определяется комбинацией двух кривых.

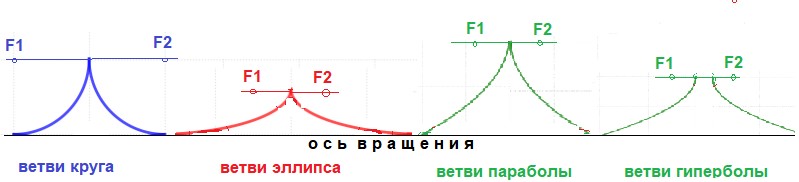
Рис. № 2. Образующий профиль

– Геометрическая метрика задаётся не только радиальной функцией R(z), но и её первой и второй производными (определяющими главные кривизны κ₁ и κ₂).

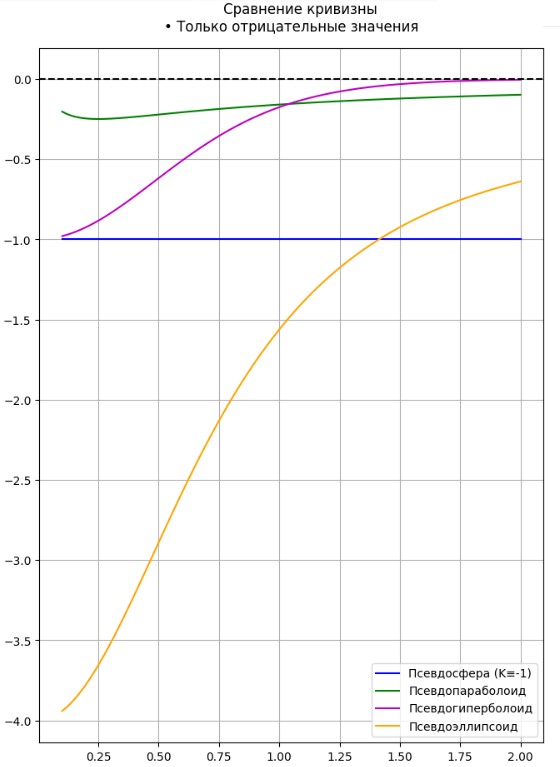
Рис. № 3. Сравнительные кривизны всех псевдоповерхностей

– Отрицательная Гауссова кривизна и фокусы исходных кривых (эллипс, парабола, гирпебола) позволяют добиваться сложных траекторий в концентрации и распространении волн.

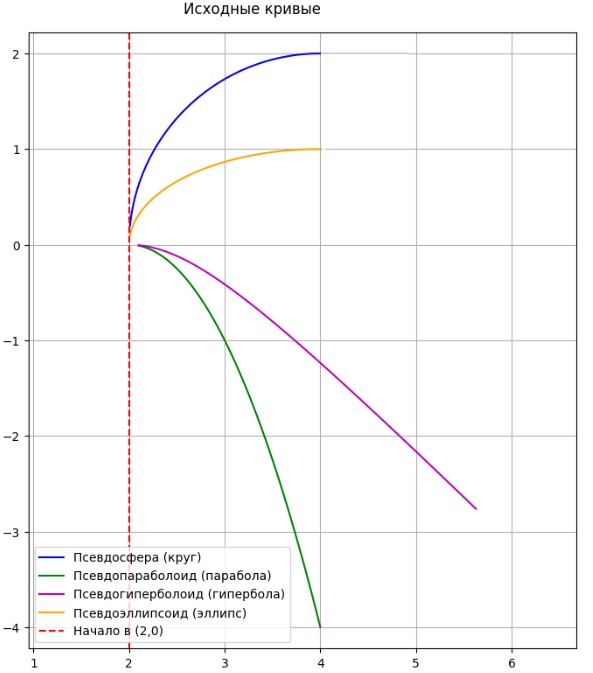
Рис. № 4. Исходные кривые для построения псевдоповерхностей

Примеры псевдоповерхностей с открытым верхом и низом

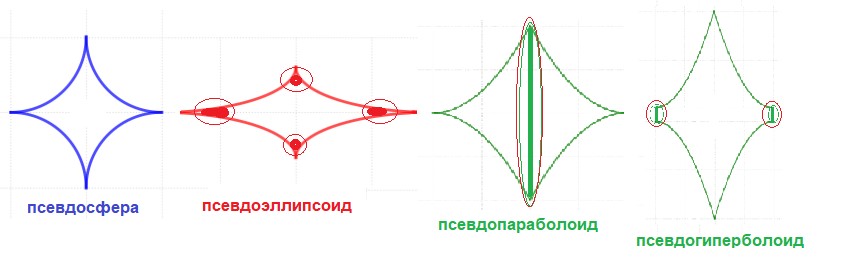
Рис. № 5. Фокальные места псевдоповерхностей

Рис. № 6. Общая форма для всех псевдоповерхностей

– Центральное тело имеет форму колоколообразной или двойной воронкообразной полости с замкнутыми или открытыми краями, создающей условия для циркуляции и усиления волн вдоль поверхности.

Уникальность данных структур состоит в том, что распространение волн приобретает уникальные свойства, выходящие за рамки классических моделей линзовой фокусировки. Волна, попав внутрь такой структуры, начинает распространяться по сложной геодезической сети, кратно отражаясь и преломляясь в процессе взаимодействия с искривлёнными границами. Каждое отражение сопровождается изменением направления, фазы и локальной плотности энергии фронта, что формирует состояние когерентной суперпозиции множества частично пересекающихся и интерферирующих волн. В результате формируются устойчивые энергетические паттерны – так называемые фокусные зоны обратной геометрической связи.

1. Образование нескольких устойчивых фокусных зон

Отличительной особенностью волн на поверхностях с переменной отрицательной кривизной является возможность возникновения не одного, а нескольких пространственно разделённых, но энергетически взаимосвязанных фокусных областей. По мере накопления отражений и дифракций волна стабилизируется в виде циркулирующих мод, распределённых между двумя и более фокусами. Эти фокусные точки соединены друг с другом нелинейными геометрическими каналами – перешейками, горловинами, кольцевыми переходами. Их форма и глубина задают траекторию энергии и обеспечивают мгновенную ответную реакцию одного фокуса на возмущение в другом.

Таким образом, попавший внутрь псевдоповерхности сигнал ведёт себя подобно жидкости в замкнутой системе – он спонтанно настраивается, перераспределяется и циркулирует между зонами концентрации. Это приводит к уникальному режиму геометрически индуцированной самоорганизации, при котором:

– происходит резкое усиление устойчивых пространственно-фазовых мод;

– наблюдается динамика быстрого обмена энергией между удалёнными зонами;

– устанавливается локальная стабильность на фоне глобальных колебаний.

2. Физические механизмы пространственной кооперации волн

– Феномен быстрой связи:

Изменение энергетического баланса в одной фокусной области практически мгновенно сказывается на потенциале остальных. Передача не требует линейных или проводящих соединений – она выражается через форму пространства и геометрию распространения волн. Это напоминает аналог нелинейной квантовой связи, но с чисто классическим вкладыванием энергии в фазовую карту поверхности.

– Режимы коллективного возбуждения:

При возбуждении одного фокуса остальные зоны могут переходить в согласованный режим автоколебаний или резонанса. Такие состояния аналогичны эффектам коллективной модовой синхронизации в резонансных кристаллах, но реализуются через кривизну, а не регулярную структуру.

– Геометрическая настройка резонансов:

Небольшое изменение угла кривизны, глубины седловины или длины перешейка между участками влияет на частоту резонансного состояния поверхности. Это обеспечивает возможность спектральной или частотной перенастройки без изменения состава среды – исключительно за счёт геометрической модификации. Таким образом, предлагаемые псевдоповерхности являются естественным продолжением и углублением классического представления о псевдосфере, открывающим новые горизонты в сфере волновой инженерии.

3.2.1 Псевдопараболоид 2-го порядка

Псевдопараболоид 2-го порядка представляет собой один из базовых представителей нового класса аксиально-симметричных псевдоповерхностей с переменной отрицательной Гауссовой кривизной (K < 0), активно применяемых в геометрической волновой инженерии (ГВИ). Он является обобщением и геометрическим усложнением классического параболоида вращения, но – в отличие от него – построен так, чтобы обеспечить не локальную (точечную), а распределённую фокусировку волновых фронтов без возникновения концентрированной каустической области.

Благодаря сочетанию отрицательной кривизны и направленной симметрии, псевдопараболоид 2-го порядка демонстрирует уникальное поведение волн: постепенное сжатие волнового фронта, усиление плотности энергии по направленной оси и формирование устойчивых фокусных зон вдоль контура, а не исключительно в фокусе, как в обычной положительной кривизне.

1. Геометрическая структура

Псевдопараболоид строится вращением специально подобранной кривой вокруг оси, смещённой относительно её оси симметрии.

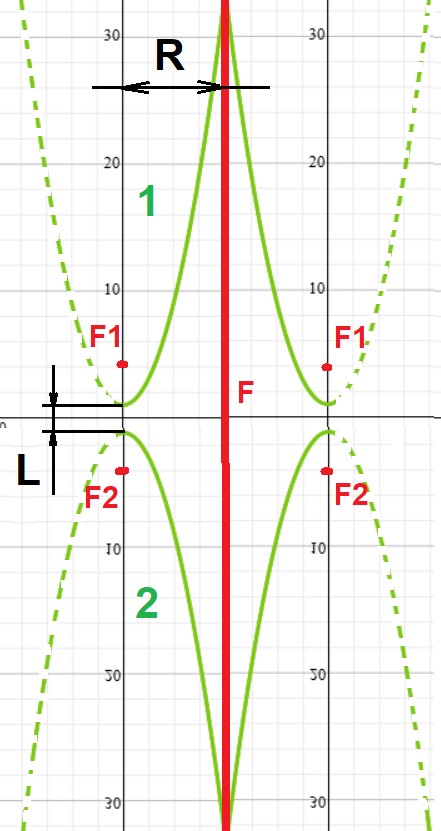
Рис. 7. Образующий профиль псевдопараболоида

– Образующая линия представляет собой модифицированную параболу, в которую введена отрицательная кривизна за счёт "седлового" изгиба или вложенной гиперболической компоненты.

– Метод построения: вращение профиля r(z) вокруг оси, смещённой от центра на d ≠ 0. Это создает асимметричную поверхность, в которой кривизна меняется по высоте и радиусу.

– Виден ярко выраженный центральный канал, сужающийся к основанию, и расширяющаяся верхняя часть, формирующая геометрическое "горло" – аналог входного объектива в волновом смысле.

– Гауссова кривизна в каждой точке:

K(z, r) = κ1(z, r) × κ2(z, r),

где κ1 > 0, κ2 < 0

Это гарантирует, что поверхность обладает седлообразной геометрией в каждой точке.

2. Волновые свойства

Благодаря гиперболической геометрии, псевдопараболоид 2-го порядка оказывает сложное воздействие на волновые фронты:

– Направленная фокусировка: волна, попадающая на область с плавным градиентом кривизны, постепенно сужается в одном направлении (как в параболе), но без образования физической точки фокуса. Вместо этого создаётся линейная или кольцевая область максимальной интенсивности.

– Зонная фокусировка: вместо простой точки фокусировки формируется вытянутая вдоль оси область, содержащая энергетически насыщенные линии волн – оптимально для стабилизации мод и защиты от аберраций.

– Подавление возвратных каустик: в отличие от обычных линз, в которых малейшая погрешность нарушает фокус, здесь волна естественным образом «размазывается» вдоль фокусной зоны, что делает такие структуры устойчивыми к внешним возмущениям и допускающими широкополосные режимы.

– Волновая ловушка: при заданных граничных условиях (например, открытость снизу и закрытость сверху) волна может реверсировать и многократно отражаться вдоль центральной оси, создавая условия для резонансной задержки.

– Интерференционные моды: за счёт повторных отражений и фазовых сдвигов между внутренними кольцевыми траекториями возникают устойчивые стоячие волновые структуры, аналогичные модам ВЧ-резонаторов.

3. Сравнение с классическими параболоидальными системами

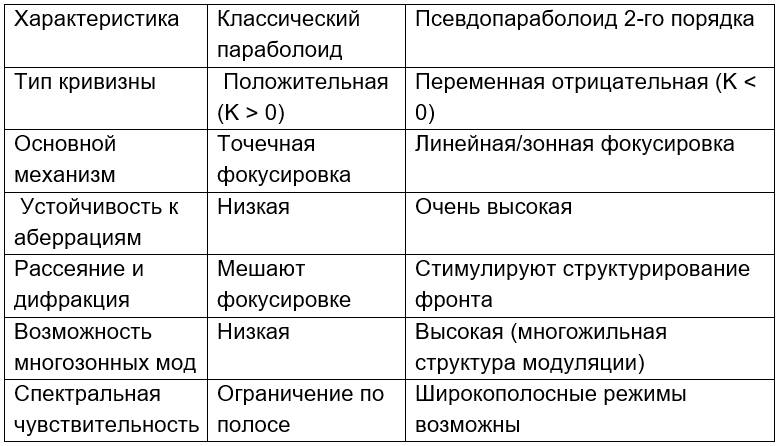
4. Применения

Благодаря своим уникальным свойствам псевдопараболоид 2-го порядка находит применение в самых различных направлениях науки и техники:

– Терагерцовые и СВЧ-антенны: возможность направленного излучения с апертурой, не привязанной к стандартной геометрии линз.

– Волновые концентраторы: создание зон усиления поля без необходимости во внешнем напряжении – оптимально для датчиков, плазмонов и нанофотонных устройств.

– Акустика и вибрационные системы: локализация звукового давления вдоль направляющих каналов без классических резонаторных эффектов.

– Лабораторные резонаторы: для изучения мод Гельмгольца в замкнутых или открытых областях с геометрической самофокусировкой.

– Оптоакустические и биосенсорные платформы: локализация, усиление и контроль волновых взаимодействий на нано- и микроскопическом уровне.

5. Технологические перспективы

Как и другие псевдоповерхности, псевдопараболоид может быть реализован с использованием аддитивных технологий (3D-печать, фото полимеризация), формирования плазмонных/метаслоёв с вариативной толщиной и нано структурирования диэлектриков и проводящих пленок. Возможны версии:

– из диэлектрических и фотонных кристаллов;

– из акустически поглощающих/отражающих композитов;

– из гибких подложек с настраиваемой геометрией;

– нано литографические реализации с точной кривизной на масштабе L.

Таким образом псевдопараболоид 2-го порядка – это геометрическая инновация, воплощающая принципы гиперболической оптики и акустики в инженерную практику. Его возможность формировать устойчивую фокусировку без жёсткого ограничения на точку, а также переносить волновую энергию в распределённые зоны без потерь, делает его универсальным и высокоинтеллектуальным компонентом будущих волновых систем.

Это не просто «объектив без линзы», а интеллектуальное геометрическое устройство, в котором форма задаёт функциональность. В контексте ГВИ он представляет собой одну из наиболее сбалансированных поверхностей по характеристикам: направленность, устойчивость, спектральная гибкость и технологическая реализуемость.

3.2.2 Псевдогиперболоид 2-го порядка

Псевдогиперболоид 2-го порядка представляет собой одну из наиболее выразительных и функционально насыщенных форм в классе псевдоповерхностей с переменной отрицательной кривизной, используемых в геометрической волновой инженерии (ГВИ).

Этот объект наследует черты классического гиперболоида однополостного, но его геометрия целенаправленно модифицирована с включением переменной (градиентной) отрицательной Гауссовой кривизны (K < 0), что придаёт ему уникальные волновые свойства – способность к удержанию, перенаправлению и пространственной организации волн различных типов.

Псевдогиперболоид 2-го порядка – это не просто обобщение геометрической формы, но и функциональный «волновой инструмент», в котором кривизна становится управляющим параметром локализации, циркуляции и обмена энергии.

1. Геометрическая структура

Псевдогиперболоид формируется вращением усечённой гиперболы вокруг оси, смещённой относительно центра симметрии.

Основные особенности конструкции:

– Образующая линия: усечённая гипербола;

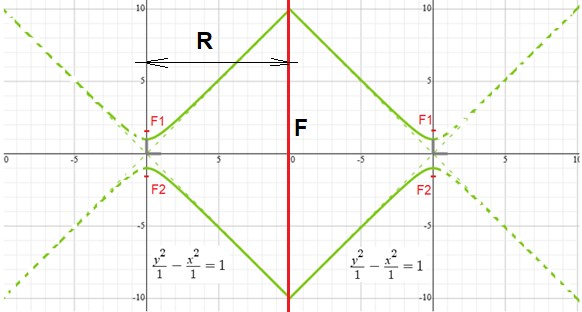
Рис. № 8. Образующий профиль псевдогиперболоида

– Метод построения: вращение образующей относительно оси Z, проходящей не через вершину фигуры, как в классическом гиперболоиде, а со смещением. Это создаёт асимметрию и вариативность кривизны.

– Гауссова кривизна: переменная, отрицательная во всём объёме структуры:

K(z, r) = κ1(z, r) × κ2(z, r) < 0

где κ1, κ2 – главные кривизны, имеющие противоположные знаки и меняющиеся по z и r.

– Общая форма: тело вращения с характерной воронкообразной геометрией, сужающееся к центру и расширяющееся к верхней и нижней части, формируя две открытые «воронки», соединённые каналом.

Такая структура напоминает двойное гиперболическое «горлышко» песочных часов и используется для создания спонтанно циркулирующих волновых полей.

2. Волновые свойства и физические эффекты

Благодаря геометрии с двойной воронкой и переменной отрицательной кривизной, псевдогиперболоид эффективно управляет поведением волн по целому спектру параметров:

– Циркуляционная траектория фронта

Волна, входящая с одной стороны, по мере приближения к горловине претерпевает ускоренное преломление и появляется возможность полного внутреннего распространения без выхода наружу. Волна проходит через горло, многократно отражается от внутренних стенок по экспоненциально расходящимся геодезическим, после чего-либо выходит в другую воронку, либо возвращается к первой – создавая условия для циркуляции аналогично кольцевым резонаторам.

– Фокусная динамика двойного типа

Фокусировка может происходить одновременно или в цилиндрической оси фокусов или в двух симметричных относительных точках – на входе и выходе горловины. Таким образом, вместо точечной фокусировки (как у линзы), псевдогиперболоид создает многозонную, пространственно фокусную структуру.