
Полная версия
Маркант

Михаил Масленников
Маркант
Предисловие
Нынешнему молодому поколению трудно в это поверить, но в середине 70-х годов прошлого века в СССР не было никаких компьютеров. Практически никаких, из тех, про которые можно было бы сказать, что они сделаны по-человечески. В своей книге КиС (Криптография и Свобода – см. https://mikhailmasl.livejournal.com/4852.html) я приводил пример компьютера (ни в коей мере не персонального!) Рута 110, стоявшего на первом этаже здания по адресу Большой Кисельный переулок, дом 11, в котором в то время размещался 4 (Технический) факультет Высшей Краснознаменной школы КГБ СССР имени Ф.Э.Дзержинского. Заметьте: не в комнате, а именно в здании, ибо Рута 110 занимала несколько комнат. Нас, молодых слушателей 4 факультета середины 70-х годов особенно умилял предбанничек к этому комплексу комнат, в котором требовалось перед входом в эту сокровищницу советской электроники одеть на сапоги музейные тряпочные тапочки. От пыли и грязи Рута 110 часто ломалась, да и от множества других явных и неявных причин тоже.
Уровень интеллекта и образованности большинства преподавателей 4 факультета был намного выше, чем возможности, которыми обладала Рута 110. Они прекрасно понимали, что будущее – за интегральными микросхемами, многоразрядными процессорами, за миниатюризацией и автоматизацией производства элементной базы будущих вычислительных устройств и не только вычислительных. На 4 факультете готовили специалистов-криптографов, которые в дальнейшем будут иметь дело с шифровальной техникой. Тогда, в середине 70-х, шифровальная техника в чем-то была похожа на Руту 110: громоздкая, неудобная, часто ломающаяся. А на западе уже стали появляться первые признаки научно-технической революции в виде надежной и миниатюрной микроэлектроники.
Анекдот советского времени. Военный парад на Красной площади. Перед мавзолеем проходят бронетранспортеры, пушки, танки, ракеты. И вдруг на огромном тягаче везут что-то непонятное.
Брежнев спрашивает у министра обороны
– Что это?
– Это наша большая интегральная схема, самая большая в мире!
НИР «Проба»
Первому начальнику 4 факультета Ивану Яковлевичу Верченко удалось собрать на факультете целую плеяду замечательных преподавателей, которые были нашими учителями и наставниками в середине 70-х. Иван Яковлевич надеялся, что факультет со временем должен был стать центром научной мысли в определенных областях специальных исследований.
В 1977 году под руководством замечательного преподавателя, начальника специальной кафедры СК-13 (кафедры высшей математики) доктора физико-математических наук, профессора Михаила Михайловича Глухова открыли НИР «Проба», в которой пытались применить западный прогресс в микроэлектронике для построения шифров, кардинально отличающихся от большинства советских шифров того времени. Они получили название «Шифры на новой элементной базе». В чем же заключалось это отличие? Давайте проведем небольшой экскурс в историю криптографии.
Начнем с дисковых шифраторов. Первый дисковый шифратор «Энигма» запатентовал в 1918 году немец Артур Шербиус. По своим функциональным возможностям и, если так можно сказать современным языком, интерфейсу он был похож на телеграфный аппарат. Разница в том, что при нажатии на клавишу с какой-то буквой открытого текста на входе на выходе появлялась другая буква шифрованного текста. Но это фактически был телеграфный аппарат, большие объемы информации передать по нему сложно, ввод – ручной.
С появлением первых, пусть даже самых примитивных ЭВМ становится понятно, что принципы шифрования информации надо изменить. Перед шифрованием надо провести оцифровку информации, т.е. перевести всю шифруемую информацию в бинарный вид, включающий в себя только два символа: 0 и 1, а затем уже шифровать полученную бинарную информацию. Такие шифраторы в середине 70-х годов называли электронными, теории электронных шифраторов на 4 факультете была посвящена специальная дисциплина СД – 7 В. Говоря специфическим криптографическим языком, в электронных шифраторах осуществлялось преобразование символов бинарного алфавита, состоящего только из двух символов: 0 и 1. А если еще более научно – над полем Галуа GF(2) из двух элементов.
Существующая в те времена в СССР элементная база, на основе которой строились шифраторы, была ориентирована на советскую электронику того времени, на диоды, транзисторы, конденсаторы и прочую подобную продукцию, которая занимала, как и в случае с Рутой 110, много места, была ненадежной и прихотливой. А на западе сначала осторожно, а потом все смелее и шире, стали появляться интегральные микросхемы. Нам, слушателям 4 факультета, в середине 70-х рассказывали о том, что сначала стоимость чипа интегральной микросхемы была сопоставима со стоимостью аналогичного по размеру куска золота. Но такие чипы оказались настолько востребованными, что среди их производителей появилась сильная конкуренция за рынки, за потребителей, все, что и должно было произойти в условиях развитого капитализма. Как следствие такой конкуренции – стремительное удешевление чипов и расширение их функциональных возможностей.
Обрабатывать информацию побитно – неэффективно. Гораздо более эффективно обрабатывать информацию сразу целыми векторами из N бит. Вектор из 8 бит называется байтом и принципиальным отличием микропроцессоров сразу после их появления стала обработка информации не битами, а байтами. Такие микропроцессоры получили название 8 разрядных. Довольно быстро после 8 разрядных стали появляться 16 разрядные, затем 32 разрядные. В настоящее время наиболее распространенными в компьютерах являются 64 разрядные микропроцессоры.
В НИР «Проба» была поставлена задача создания и анализа узлов для криптосхем, работающих не с битами, а с байтами. Формально каждый байт является 8 битовым вектором и с ним можно работать так же, как и раньше работали с электронными шифраторами. Но будет ли такая работа наиболее эффективной? Можно ли найти для шифраторов, работающих с байтами, специфические методы построения более высокоскоростных и более стойких шифраторов, чем традиционные электронные?
Как я писал в КиС, большинство советских шифраторов того времени состояли из «балалаек». Так криптографы прозвали типовой узел тех шифраторов, состоящий из регистра сдвига над GF(2) и его функции обратной связи. А что будет, если ячейками регистра сдвига будут не биты, а байты? Или, опять переходя к математическому языку, регистр сдвига будет над Z/256 – кольцом вычетов по модулю 256. Появляются два интересных момента.
Сложение байт можно проводить как покоординатное сложение по модулю 2 без переноса, а можно как сложение в кольце Z/256 – с переносом;
К содержимому ячейки можно применять подстановку из симметрической группы S256.
В НИР «Проба» сфокусировали внимание именно на этих двух особенностях перехода от бит к байтам. Как и во всякой серьезной НИР, начали с изучения простейших свойств, не пытаясь сразу объять необъятное. Первый отчет по НИР «Проба» вышел в 1977 году, с тех пор прошло уже свыше 40 лет.
Сейчас результаты НИР «Проба» позволяют понять, чем же интересовались в середине 70-х годов прошлого века советские криптографы, каковы были тогда основные направления развития криптографии, как специфического раздела математики. Я, естественно, не могу в точности помнить все эти результаты, полученные свыше 40 лет назад, но постараюсь здесь вкратце описать их общими словами.
Ключевым словом в НИР «Проба» было слово подстановка. В математике так принято называть взаимно-однозначное отображение некоторого множества в себя. Множество всевозможных подстановок принято называть симметрической группой. Так, любая подстановка из симметрической группы S256 – это взаимно-однозначное отображение кольца вычетов Z/256 в себя.
Имея всего 256 байт памяти легко реализовать на них любую подстановку π из S256. Для этого для любого x ϵ Z/256 в ячейку памяти по адресу x надо записать значение π(x).
В алгебре под произведением подстановок понимают их последовательное применение слева направо.
Операцию сложения с переносом двух байт x и y тоже можно рассматривать как подстановку gx ϵ S256: gx(y) = (x + y)mod 256. Если через g обозначить полноцикловую подстановку g = g1 = (0,1,2,…,255), то, полагая, что g0 – это единичная подстановка, когда все элементы отображаются сами в себя, получаем, что при любом x ϵ Z/256 gx = gx .
Множество всевозможных преобразований {g0, g1,…,g255} образуют циклическую группу, которую в НИР «Проба» было принято обозначать G =
Предположим, что у нас есть цепочка байт x1, x2,…xk и произвольная подстановка π из S256. Что можно сказать о подстановках gx1π gx2π… gxkπ?
Одним из первых и очень важным результатом НИР «Проба» было доказательство, что при случайном и равновероятном выборе π из S256 группа, порожденная множеством Gπ, с большой вероятностью совпадает со всей симметрической группой S256. Что это означало на практике?
Возьмем простейший типовой узел, реализованный с помощью побайтных преобразований.
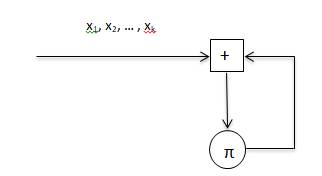
Рис. 1. Типовой узел (Gπ)k
На вход узла подается входное слово – цепочка из k байт, каждый байт складывается по модулю 256 с результатом обработки предыдущих байт и заменяется по подстановке π. Таким образом, этот узел работает циклами, в каждом цикле по k тактов. Если предположить, что цепочка X = x1,x2,..,xk из k байт является ключом, то с помощью этого узла можно реализовать подстановку π1 = gx1π gx2π… gxkπ, зависящую от ключа X. Результаты НИР «Проба» показывают, что таким путем можно реализовать практически любую подстановку из S256.
Здесь хотелось бы обратить внимание на то, что группа
А теперь давайте вернемся ко второй мировой войне и немецкому дисковому шифратору «Энигма». В нем было два типа ключей: долговременные и одноразовые. Долговременные ключи – это коммутации вращающихся роторов, а одноразовые – их начальное положение. Если коммутации вращающихся роторов неизвестны, то в этом случае криптографы бессильны. Коммутации роторов – это фактически подстановки на множестве букв немецкого алфавита. Число всевозможных подстановок в симметрической группе SN равно N! – N факториал, произведение всех чисел от 1 до N. При N = 26 имеем N! = 403 291 461 126 605 635 584 000 000 ≈ 4 * 1026. Если предположить, что в «Энигме» коммутации роторов выбирались случайно и равновероятно, то для перебора всевозможных значений коммутации только одного ротора потребовалась бы трудоемкость, непосильная даже для современных ЭВМ. Поэтому англичане могли читать «Энигму» только при условии, что какими-то путями им удалось захватить хотя бы один ее экземпляр и определить коммутации всех роторов.
Роторы в «Энигме» нельзя было сделать одноразовыми ключами по объективным причинам – это слишком сложно. А в НИР «Проба» показали, что в шифрах на новой элементной базе это сделать несложно.
Итак, неограниченно увеличивая k – длину входного слова, с помощью цепочек gx1π gx2π… gxkπ можно получить любую подстановку из S256. Но это – абстрактный результат, а хотелось бы знать, что за подстановки будут при каком-нибудь фиксированном k. Какими свойствами будет обладать при фиксированном k множество таких подстановок при всевозможных x1, x2,…,xk? Такое множество принято обозначать (Gπ)k.
Во многих криптографических задачах важную роль играет свойство 2-транзитивности некоторого множества подстановок. Множество подстановок (Gπ)k является 2-транзитивным, если для любых двух пар (x1,y1) и (x2,y2), таких что x1 ≠ y1 и x2 ≠ y2, найдется подстановка, переводящая пару (x1,y1) в (x2,y2).
В НИР «Проба» получили следующие результаты.
Минимальное значение k, при котором (Gπ)k является 2-транзитивным, равно 3.
При случайном и равновероятном выборе π из S256 с вероятностью, близкой к 1, множество (Gπ)3 будет 2-транзитивным.
Для любой подстановки π из S256 можно определить ее так называемую матрицу частот P(π) размера 255 х 255, у которой на пересечении строки с номером i со столбцом с номером j, i,j ϵ {1,2,…,255}, находится число решений системы
x – y = i (mod 256)
π(x) – π(y) = j (mod 256)
относительно неизвестных x, y ϵ Z/256.
В НИР «Проба» показали, что множество (Gπ)3 является 2-транзитивным тогда и только тогда, когда возведенная в квадрат матрица P(π) не содержит нулевых элементов. Чуть позже было доказано, что при случайном и равновероятном выборе π в матрице P(π) примерно 2/3 элементов – ненулевые, 1/3 – нули.
Темой моей дипломной работы в 1979 году было построение и анализ матриц P(π) для всех π из симметрической группы S8. Это 8! = 40320 подстановок. Такое построение позволяло подтвердить приведенные выше теоретические результаты.
Для Руты – 110, если она к тому времени была еще жива (сейчас точно не помню), это явно непосильная задача, матрицы строились вручную. Все теоретические результаты были подтверждены.
Ангстрем – 3
После изучения в НИР «Проба» математического аппарата для шифров на новой элементной базе естественно встал вопрос о построении простейшего примера такого шифра.
Здесь мне хотелось бы сказать несколько слов о том, кто тогда, на рубеже 80-х годов прошлого века, занимался в СССР криптографией и шифрами.
Специалистов-криптографов готовили только на 4 факультете ВКШ. Их отбирали и направляли на учебу 3 ведомства: КГБ, Министерство обороны и НИИ Автоматики. После окончания 4 факультета выпускники направлялись на службу в то ведомство, которое их набирало на учебу. Выпускники от КГБ и МО становились действующими офицерами, хотя военную форму в КГБ не носили, а выпускники от НИИ Автоматики – офицерами запаса, не получающими льгот и выплат, положенных действующим офицерам, хотя во время учебы на 4 факультете были военнослужащими и ходили в военной форме. В прошлом НИИ Автоматики – спецтюрьма № 16 МВД СССР, в 1948 году преобразована в спецтюрьму № 1 МГБ СССР, эта спецтюрьма известна по роману А.И.Соженицына «В круге первом».
Разработкой новых советских шифров должно было заниматься НИИ Автоматики, а Спецуправление 8 ГУ КГБ СССР – проводить их экспертизу. В реальной жизни разработка и экспертиза тесно переплетались и превращались в совместную работу криптографов, закончивших 4 факультет.
После окончания 4 факультета в 1979 году я попал на работу в 5 (Теоретический) отдел Спецуправления 8 ГУ КГБ СССР. Там тогда тоже интересовались шифрами на новой элементной базе, поддерживали тесные связи с НИИ Автоматики. В группе Валерия Владимировича Ященко, в которую я попал, вели следующий, если так можно выразиться, «анализ идеи» построения шифра на новой элементной базе с помощью неавтономного регулярного регистра сдвига над Z/256, которую принесли в 5 отдел Владимир Владимирович Седов и Борис Владимирович Березин из НИИ Автоматики.
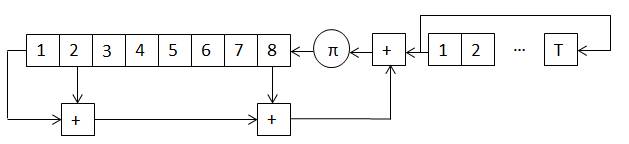
Рис. 2. Шифратор «Ангстрем – 3»
В этой идее самое привлекательное – простота ее реализации. В НИИ Автоматики, по-видимому, поддерживали связи с заводом «Ангстрем» в Зеленограде, который в то время являлся ведущим предприятием по выпуску советской электроники. В.В.Седов и Б.В.Березин заканчивали 4 факультет, знали о НИР «Проба» и пытались перейти от чисто абстрактных математических результатов к конкретным шифраторам. Изображенный выше неавтономный регулярный регистр сдвига над Z/256 получил название шифратор «Ангстрем – 3». Слово «Ангстрем», по-видимому, предполагало, что он будет реализован на элементной базе завода Ангстрем, а цифра 3 – что это была не первая такая попытка.
Я подробно описывал в КиС, как мне удалось взломать «Ангстрем – 3» при T = 16 и как к этому отнеслись мои новые начальники. «Ангстрем – 3» взламывался на спор, я этот спор выиграл и получил за это прибавку к жалованию. Дальше, естественно, встал вопрос: а как можно модифицировать «Ангстрем – 3» так, чтобы сделать его стойким и сохранить простоту реализации?
Первая и самая необходимая модернизация – переставить подстановку.
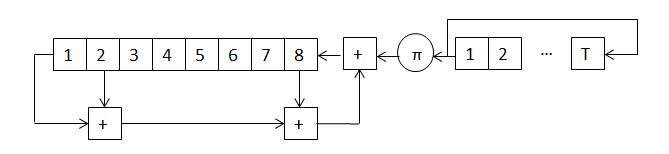
Рис. 3. Шифратор «Ангстрем – 3 М»
Почему использование подстановки π до, а не после операции сложения с функцией обратной связи более целесообразно? Давайте немного окунемся в математику и в проведенный в 5 отделе СУ 8 ГУ КГБ СССР «анализ идеи» шифратора «Ангстрем – 3». Я неспроста употребил здесь такой странный термин, как «анализ идеи». Сам шифратор может строиться по-разному, это может быть блочный шифр (простая замена большой степени), а может быть шифр гаммирования. Но анализ в любом случае проводится в следующих предположениях.
Ключом является входное слово (последовательность байт) x1,x2,…,xT, записанное в правом регистре;
Цикл работы состоит из T тактов, за каждый такт состояние левого регистра сдвигается на одну ячейку влево и в крайнюю правую ячейку добавляется функция обратной связи, зависящая от состояния и очередного байта ключа;
Подстановка π – известна;
Известны несколько начальных и соответствующих им конечных состояний левого регистра.
При таких предположениях ставится задача: определить неизвестный ключ, т.е. входное слово x1,x2,…,xT.
Обозначим состояния левого регистра.
– y1,y2,…,y8 начальное состояние;
– y9,y10,…,yT промежуточное состояние;
– yT+1,yT+2,…,yT+8 конечное состояние.
При T ≤ 8 промежуточное состояние отсутствует.
Для шифратора «Ангстрем – 3» при любом i ϵ {1,2,…,T} будет справедливо следующее соотношение:
y8+i = π(yi + y1+i + y7+i + xi) =>
π-1(y8+i) = yi + y1+i + y7+i + xi =>
π-1(y8+i) = ππ-1(yi) + ππ-1(y1+i) + ππ-1(y7+i)+ xi.
Заменив в этих соотношениях π-1(yi) на zi при всех i от 1 до T+8, получаем систему уравнений, в которую ключевые параметры xi входят линейно. Для криптографа это – катастрофа, как конкретно взламывается «Ангстрем -3» при T = 16 можно прочитать в КиС.
Если подстановку π переставить и использовать до, а не после операции сложения с функцией обратной связи, то такого линейного вхождения знаков ключа уже не будет.
Изучению шифраторов типа «Ангстрем – 3» в начале 80-х годов в 5 отделе СУ 8 ГУ КГБ СССР была посвящена НИР «Мотив». Закончилась она созданием заявки на изобретение.

Рис.4. Авторское свидетельство на шифратор «Ангстрем – 3».
17 мгновений весны
Сцена из культового советского сериала «17 мгновений весны».
«Мюллер только что получил сообщение из центра дешифровки о событиях на конспиративной явке гестапо в Берне. Сравнивая эти два шифра, он сейчас сделал неожиданное, но чрезвычайно существенное открытие. От предчувствия удачи у него даже заболела голова. Шифр русской радистки совпадал с шифром связника из Берна.»
Смех душит меня от этой умилительной сцены. Генерал Мюллер не спит, а занимается тем, что должен был для него сделать молоденький лейтенант – первичным криптоанализом шифртекста.
А теперь взглянем на «шифр русской радистки» и сравним его с «шифром связника из Берна».
Точнее – посмотрим на все то, что в сериале выдается за шифры.

Рис. 5. Шифровка 1. Подлинник шифровки русской радистки.

Рис. 6. Шифровка 2.

Рис. 7. Шифровка 3.
Я не знаю, смотрел ли до меня кто-нибудь внимательно на эти «шифровки».
Не две, а три, все разные.
Все почему-то содержат ровно 15 групп из 5 цифр.
Все начинаются с одной и той же группы 51123, что заметил Мюллер.
В шифровках 2 и 3 первые группы второй строки очень похожи: 62345 и 63452. Этого Мюллер не заметил, а если бы первичный криптоанализ проводил не генерал, а молодой лейтенант, то уж он-то это сходство подметил бы.
И так далее.
Вывод можно сделать только один. В тех шифрсообщениях, которые в сериале «17 мгновений весны» преподносятся зрителю как шифровки, составленные русским агентом Штирлицем, нарушено самое фундаментальное правило криптографии: шифрсообщения не должны отличаться от набора случайных и равновероятных значений.
Если это правило нарушено, то шифровки такого агента могут выделяться при проведении первичного криптоанализа, что грозит агенту провалом.
Неужели Штирлиц, проработавший в разведке много лет, не понимал, что если все его шифровки начинаются с 51123, то это для него смертельно опасно? Просил ли он Центр сменить такой никудышный шифр?
Можно придумать множество способов шифрования, точнее даже не шифрования, а кодирования секретных сообщений. При кодировании, наряду с сокрытием содержимого сообщения, можно сокращать его длину, ставя в соответствие каким-то длинным и часто используемым фразам короткие кодовые значения. Но после кодирования необходимо перешифровать закодированный текст с помощью случайной и равновероятной гаммы наложения.
Забегая вперед и чтобы заинтриговать читателя могу сказать, что именно необходимость перешифровки закодированного текста спасла в 1992 году Россию от потока фальшивых чеченских авизо.
Просил ли Штирлиц Центр сменить свой квази-шифр на что-то более стойкое, я не знаю. Но современные Штирлицы просили и просили очень настойчиво. Люди, работавшие на Первое Главное управление КГБ СССР в капиталистических странах, в середине 80-х годов уже стали привыкать к западному научно-техническому прогрессу, к первым персональным компьютерам и даже к портативным персональным компьютерам, помещавшимся в портфель. И они никак не могли понять: почему в условиях такого стремительного прогресса они должны использовать такие допотопные шифры 30-летней давности? Неужели в СССР не могут сделать шифр для портативного компьютера?
1987 год. Я закончил аспирантуру 4 факультета, защитил кандидатскую диссертацию и в конечном счете попал в 4 отдел Спецуправления 8 ГУ КГБ СССР. 5 отдел, где я работал до аспирантуры, был теоретический, а 4 – практический. Можно даже сказать, что специфический, в чем именно заключалась его специфичность – оставляю эту тему для размышления читателю.
Диссертация, которую я защитил, была целиком посвящена шифрам на новой элементной базе. Идей для их построения – масса, как бы теперь реализовать что-нибудь на практике. На советской элементной базе того времени? Рута 110, за что ей спасибо, надолго отбила всякую охоту к подобным изысканиям. А на чем?
В 4 отделе я получил должность небольшого начальничка. За время учебы на 4 факультете, глядя на нашего начальника курса (см. КиС), у меня сложилось отвращение к административной работе, ко всем большим и малым начальничкам, считавшим эту работу важнее научной. А тут – сам стал начальничком. Но бонусом к должности начальничка были две неоценимые вещи: почти отдельный кабинет и чудо техники в то время – портативный персональный компьютер.
Образовалась гремучая смесь: молодому и полному идей кандидату наук дали истинно персональный, да еще и портативный компьютер и создали условия для работы, чтобы современные Штирлицы не пользовались больше всякими пещерными шифрами 30-летней давности.
Больше на эту тему говорить не буду. Перейдем к побочной продукции 4 отдела Спецуправления 8 ГУ КГБ СССР.
Побочная продукция
Побочной продукцией 4 отдела СУ 8 ГУ КГБ СССР были ручные шифры для Советской Армии. Такие огромные переговорные таблицы, тоже пещерная продукция, которой пользовались люди попроще, чем Штирлицы – солдаты Советской Армии.
В 1979 году началась война в Афганистане. Сотрудник 4 отдела СУ 8 ГУ КГБ СССР Вячеслав Шеремета побывал на ней в командировке и увидел своими глазами проблему: в боевых условиях солдаты часто игнорировали эти громоздкие переговорные таблицы и передавали по рации команды открытым текстом, что приводило к их перехвату противником и неоправданным потерям. Что-то надо было делать с этими таблицами…
Вот тут уже не обойтись без советской электроники. Точнее – западной, но освоенной заводом Ангстрем в Зеленограде.
Для точности приведу цитату из Википедии.
«В 1984 году Министерство электронной промышленности дало задание на проектирование аналога карманного персонального компьютера Casio FX-700P. Разработчики предложили использовать 16-битный процессор Н1806ВМ2, основанный на технологии КМОП аналог К1801ВМ2, процессора с системой команд популярной в СССР архитектуры PDP-11, и базовый матричный кристалл Н1515ХМ1. Несмотря на иную схемотехнику, в министерстве настояли на полном внешнем сходстве с прототипом Casio, хотя это вызвало затруднения, в частности, со схемой выключения. Переработанный для калькулятора процессор получил обозначение Т243-2, а на базовом матричном кристалле были созданы контроллер ОЗУ, ПЗУ и клавиатуры T241-2-015 и контроллер дисплея T241-2-014. Прототип на базе этих элементов серийно не выпускался, однако несколько экземпляров попали к потребителям. Для серийного образца на базе К1801ВМ2 была разработана оригинальная микросхема процессора, включившая в себя часть контролеров периферийных устройств и получившая обозначение Т36ВМ1-2, и переработанные варианты трассировки базового матричного кристалла периферийных микросхем.»








