ЕГЭ 2025. Информатика и ИКТ. Значения логических выражений. 15

Лада Есакова

ЕГЭ 2025. Информатика и ИКТ. Значения логических выражений. 15

От автора

Приветствую вас, дорогие ученики, родители, преподаватели, методисты, репетиторы! Все вместе мы начинаем подготовку к ЕГЭ по Информатике и ИКТ 2025 г.

В 2025 году структура экзаменационной работы осталась без изменений. Всего в работе 27 заданий. В экзаменационной работе, с одной стороны, присутствуют задания, требующие хорошего знания математики, логики, умения анализировать и абстрактно мыслить, с другой стороны, – задания, основанные на аккуратном, монотонном исполнении алгоритма, переборе вариантов (ученику предоставляется возможность поработать, как компьютер).

Задания 1-25 оцениваются в 1 балл, задания 26, 27 – в 2 балла. Таким образом, при абсолютно правильном решении всех задач можно заработать 29 первичных баллов. .

Экзаменационная работа по информатике очень объемная. Практика показывает, что даже сильным ученикам просто не хватает времени на решение всех задач. Многие задачи довольно простые для большей части учеников, но они часто требуют аккуратного перебора и анализа большого объема данных. Даже в случае отличного понимания предмета требования почти невыполнимые! При полном понимании хода решения задачи Вам просто не хватит времени. Здесь понимания недостаточно, важна практика, безошибочность действий, почти автоматизм в решении конкретного типа задач. А такую практику, как известно, можно получить только большим количеством повторений одинаковых, монотонных действий.

Итак, рецепт достижения нужных временных характеристик есть, но методических материалов, подборок всех типов задач, к сожалению, практически нет. Поэтому в данное методическое пособие (позадачный тренинг) я включила авторские задачи абсолютно всех типов, которые встречались в тренировочных, репетиционных и диагностических работах, в вариантах ЕГЭ по Информатике и ИКТ основной и досрочной волны 2013-2025 гг. Блоки задач расположены по возрастанию сложности. Для закрепления каждой темы в книге представлены тренировочные работы. В конце книги приведены ответы ко всем заданиям.

Отработав каждый тип заданий, научившись решать их быстро и безошибочно, вы обеспечите себе высокий балл на ЕГЭ.

Искренне желаю успехов!

Аналитическая справка

При всем кажущемся разнообразии заданий 15 (числовые отрезки, делимость, конъюнкция и пр.) все они сводятся к поиску значения параметра A, для которого указанное логическое выражение истинно (или ложно) для всех значений переменной x. А потому и решать все типы этого задания мы будем практически одинаково.

Рекомендую следующий порядок действий:

1). Вводим более короткие и понятные обозначения

Это очень важный шаг, поскольку исходное выражение может быть громоздким, преобразовать его без ошибок очень сложно.

2). Приводим выражение к виду P(x) ∨ A(x) = 1

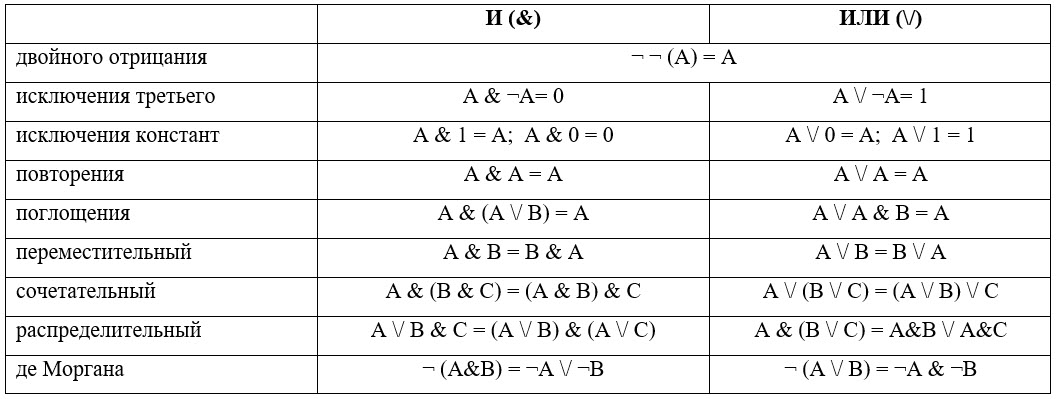
Используя приведенные ниже законы алгебры логики преобразуем исходное выражение в логическую сумму P(x) – выражение с известными значениями и A(x) – выражение с искомым параметром.

3). Заменяем исходное выражение эквивалентной системой

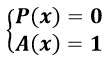
Если P(x) = 1, то логическая сумма P(x) ∨ A(x) принимает значение 1 при любом A(x) и мы не сможем его найти. Если P(x) = 0, то логическая сумма P(x) ∨ A(x) принимает значение 1 только при A(x) = 1.

4). Решаем уравнение P(x) = 0

Т.е. находим множество значений переменной х, для которых выполняется условие этого уравнения.

5). Подставляем решение первого уравнения в уравнение A(x) = 1 и находим значение A.

Можно решить эту задачу программным способом. Для этого напишем программу, которая:

1). В цикле перебирает достаточно большой диапазон возможных значений параметра A.

2). Во вложенном цикле для каждого из значений A перебирает достаточно большой диапазон значений переменной x (или переменных x, y) и подставляет в исходное выражение.

3). Если выражение принимает значений 1 для всех значений x (или переменных x, y), программа делает вывод, что текущее значение A «хорошее».

4). Из «хороших» значений A выбирает удовлетворяющее условию задачи (наибольшее, наименьшее).

Логическим операциям соответствуют следующие операции в языках программирования:

ЧИСЛОВЫЕ ОТРЕЗКИ

Тренировочная работа 1

1.      На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула

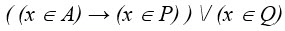
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 11]      2) [6, 10]      3) [8, 16]      4) [17, 23]

2.      На числовой прямой даны три отрезка: P = [10, 50], Q = [15, 20] и R = [30, 80]. Выберите такой отрезок A, что формула

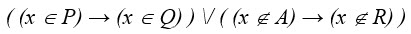
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 25]            2) [25, 50]            3) [40, 60]            4) [50, 80]

3.      На числовой прямой даны три отрезка: P = [15, 30], Q = [5, 10] и R = [20, 25]. Выберите такой отрезок A, что формула

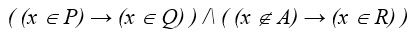
тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 20]            2) [0, 10]            3) [10, 15]            4) [25, 30]

4.      На числовой прямой даны два отрезка: P = [44; 49] и Q = [28; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула

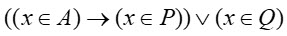
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

5.      На числовой прямой даны два отрезка: P = [15; 39] и Q = [44; 57]. Укажите наибольшую возможную длину такого отрезка A, что формула

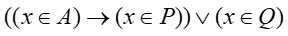
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

6.      На числовой прямой даны два отрезка: P = [25, 50] и Q = [32, 47]. Отрезок A таков, что формула

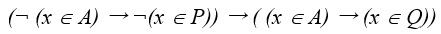
тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?

7.      На числовой прямой даны два отрезка: P = [130; 171] и Q = [150; 185]. Укажите наименьшую возможную длину такого отрезка A, что формула

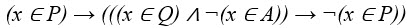
истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х.

8.      На числовой прямой даны два отрезка: P = [17, 40] и Q = [20, 57]. Отрезок A таков, что приведённая ниже формула истинна при любом значении переменной х:

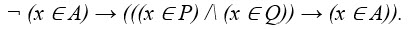
Какова наименьшая возможная длина отрезка A?

Решение тренировочной работы 1

1.      На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула

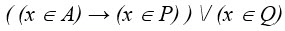
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 11]      2) [6, 10]      3) [8, 16]      4) [17, 23]

Решение:

Введем обозначения:

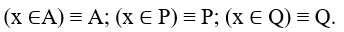
Применив преобразование импликации и заменив знак отрицания, получаем:

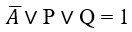
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

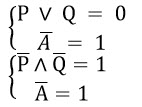
Изобразим на числовой прямой решение первого уравнения:

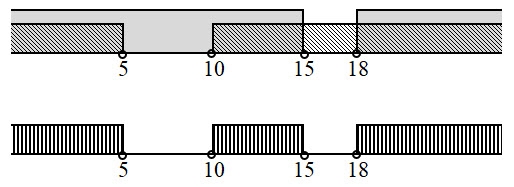
Это интервалы (-∞, 5); (10, 15); (18, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами.

Из всех отрезков только отрезок [6, 10] удовлетворяет этим условиям:

Правильный ответ указан под номером 2.

Ответ: 2

2.      На числовой прямой даны три отрезка: P = [10, 50], Q = [15, 20] и R = [30, 80]. Выберите такой отрезок A, что формула

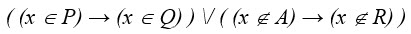
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 25]            2) [25, 50]            3) [40, 60]            4) [50, 80]

Решение:

Введем обозначения:

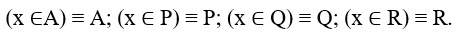
Применив преобразование импликации и заменив знак отрицания, получаем:

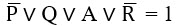
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

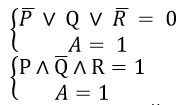
Изобразим на числовой прямой решение первого уравнения:

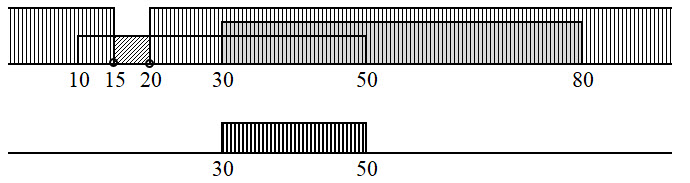
Это отрезок [30, 50]

Для него должно выполнятся условие второго уравнения. Т.е. все выделенные точки должны принадлежать отрезку A. Значит, отрезок [30, 50] полностью содержится в отрезке A.

Из всех отрезков только отрезок [25, 50] удовлетворяет этим условиям:

Правильный ответ указан под номером 2.

Ответ: 2

3.      На числовой прямой даны три отрезка: P = [15, 30], Q = [5, 10] и R = [20, 25]. Выберите такой отрезок A, что формула

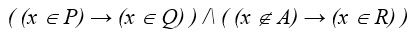
тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 20]            2) [0, 10]            3) [10, 15]            4) [25, 30]

Решение:

Введем обозначения:

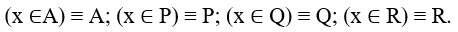
Применив преобразование импликации и заменив знак отрицания, получаем:

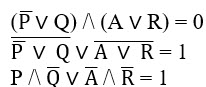
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

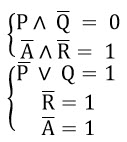
Изобразим на числовой прямой решение первого уравнения:

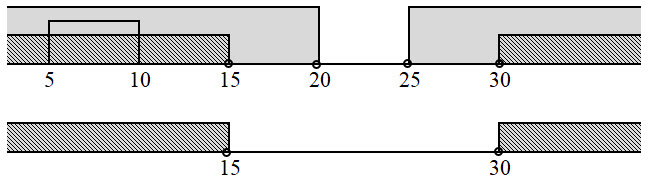
Это интервалы (-∞, 15); (30, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами.

Из всех отрезков только отрезок [25, 30] удовлетворяет этим условиям:

Правильный ответ указан под номером 4.

Ответ: 4

4.      На числовой прямой даны два отрезка: P = [44; 49] и Q = [28; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула

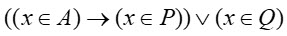
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение:

Введем обозначения:

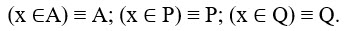
Применив преобразование импликации и заменив знак отрицания, получаем:

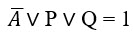
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

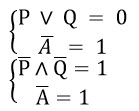
Изобразим на числовой прямой решение первого уравнения:

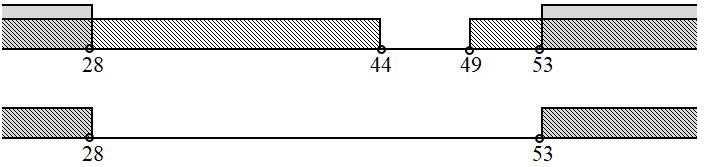
Это интервалы (-∞, 28); (53, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами. Наибольшая возможная длина такого отрезка 53 – 28 = 25. Это интервалы (-∞, 28); (53, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами. Наибольшая возможная длина такого отрезка 53 – 28 = 25.

Программный способ решения:

Ответ: 25

5.      На числовой прямой даны два отрезка: P = [15; 39] и Q = [44; 57]. Укажите наибольшую возможную длину такого отрезка A, что формула

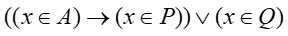
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение:

Введем обозначения:

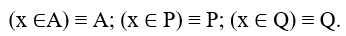
Применив преобразование импликации и заменив знак отрицания, получаем:

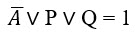
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

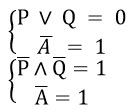
Изобразим на числовой прямой решение первого уравнения:

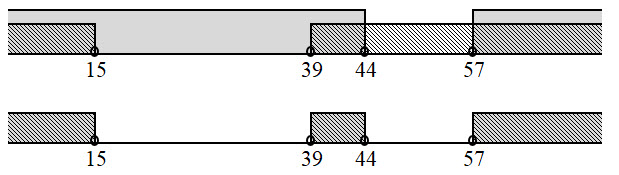
Это интервалы (-∞, 15); (39, 44); (57, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами. Выберем из отрезков [15, 39] и [44, 57] тот, который имеет большую длину. Это отрезок [15, 39]. 39 – 15 = 24.

Программный способ решения:

Ответ: 24

6.      На числовой прямой даны два отрезка: P = [25, 50] и Q = [32, 47]. Отрезок A таков, что формула

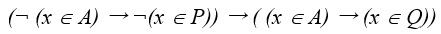
тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?

Решение:

Введем обозначения:

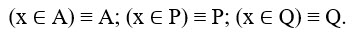
Применив преобразование импликации и заменив знак отрицания, получаем:

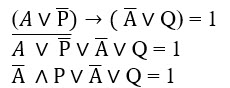
Вынесем A ̅ за скобки:

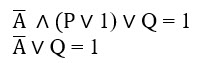
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

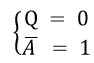
Изобразим на числовой прямой решение первого уравнения:

Это интервалы (-∞, 32); (47, +∞).

Для них должно выполнятся условие второго уравнения. Т.е. никакие из выделенных точек не должны принадлежать отрезку A. Значит, отрезок A не имеет общих точек с указанными интервалами. Максимальную длину имеет отрезок [32, 47]. 47 – 32 = 15.

Программный способ решения:

Ответ: 15

7.      На числовой прямой даны два отрезка: P = [130; 171] и Q = [150; 185]. Укажите наименьшую возможную длину такого отрезка A, что формула

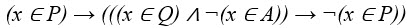
истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х.

Решение:

Введем обозначения:

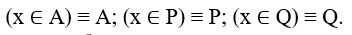
Применив преобразование импликации и заменив знак отрицания, получаем:

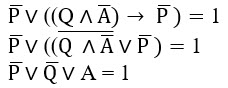
Рассмотрим случай, когда известная часть ложна, тогда искомая должна быть истинной:

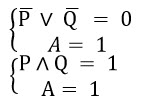
Изобразим на числовой прямой решение первого уравнения:

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.