Интегрирование и нейросети

Николай Морозов

Интегрирование и нейросети

В то время, как основной задачей дифференциального исчисления является нахождение производной, основной задачей интегрального исчисления является нахождение функции по заданной ее производной. Говоря иными словами, в случае интегрального исчисления, мы имеем дело с обратной задачей.

I.Первообразная и неопределенный интеграл

1.1.Основные понятия и определения

Определение первообразной (см.рис.1):

Рис.1.

Определение неопределенного интеграла (рис.2):

Рис.2.

Давайте попробуем основные понятия, связанные с интегральным исчислением, помочь нам сформулировать нейросети.

GPTutor

Неопределённый интеграл – это понятие математического анализа, используемое для нахождения первообразной. Неопределённый интеграл обозначается следующим образом:

∫f(x) dx

Здесь f(x) – подинтегральная функция, dx – дифференциал переменной x, а ∫ – знак интеграла. Результатом вычисления неопределенного интеграла является множество функций, отличающихся на константу.

Например, если дана функция f(x) = x^2, то её неопределённым интегралом будет F(x) = (1/3) x^3 + C, где C – произвольная постоянная.

Автор

Дайте определение первообразной

GPTutor

Первообразная функции f(x) – это функция ( F(x) ), производная которой равна данной функции f(x) . Математически это выражается следующим образом:

Если F'(x) = f(x) для всех ( x ) из некоторого интервала, то функция F(x) называется первообразной функции ( f(x) ).

Таким образом, первообразная функции f(x) является решением задачи нахождения функции F(x). Важно помнить, что первообразная не единственна, так как любая первообразная может быть получена путём добавления произвольной постоянной.

Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют любую ее первообразную функцию.

ChatGPT на русском: вход в ChatGPT онлайн MashaGPT

Неопределенный интеграл функции \( f(x) \) обозначается как \( \int f(x) \, dx \) и представляет собой множество всех первообразных этой функции. Это означает, что неопределенный интеграл возвращает функцию \( F(x) \), производная которой равна \( f(x) \):

\[F'(x) = f(x)\]

При этом к результату добавляется константа интегрирования \( C \), так как производные констант равны нулю:

\[\int f(x) \, dx = F(x) + C\]

Основные свойства неопределенных интегралов:

1. **Линейность**:

\[ \int (af(x) + bg(x)) \, dx = a \int f(x) \, dx + b \int g(x) \, dx \]

где \( a \) и \( b \) – произвольные константы.

2. **Сложение**:

\[ \int f(x) \, dx + \int g(x) \, dx = \int (f(x) + g(x)) \, dx \]

3. **Замена переменной**: Если \( u = g(x) \), то:

\[ \int f(g(x)) g'(x) \, dx = \int f(u) \, du \]

Неопределенные интегралы широко используются в математике, физике и инженерии для решения различных задач.

Первообразная функции \( f(x) \) – это такая функция \( F(x) \), производная которой равна исходной функции \( f(x) \):

\[F'(x) = f(x)\]

То есть, если мы берём производную от \( F(x) \), мы получаем \( f(x) \). Первообразная определяет неопределённый интеграл, и к ней добавляется произвольная константа \( C \):

\[\int f(x) \, dx = F(x) + C\]

Первообразная играет ключевую роль в интегрировании, позволяя находить площади под графиками функций и решать множество задач в математике и физике.

Думаю, что с определениями неопределенного интеграла и первообразной. которые дают две нейросети GPTutor и MashaGPT можно согласиться.

Все. выше сказанное.можно подтвердить примерами.

Пример 1.

Найти первообразную функции f(x) = x^2.

GPTutor

Чтобы найти первообразную функции ( f(x) = x^2 ), необходимо вычислить неопределенный интеграл этой функции:

[\int f(x) , dx = \int x^2 , dx]

Согласно правилу интегрирования степенной функции, мы прибавляем 1 к степени и делим на новую степень:

[\int x^n , dx = \frac{x^{n+1}}{n+1} + C]

где ( n \neq -1 ) и ( C ) – произвольная константа интегрирования.

В нашем случае ( n = 2 ):

[\int x^2 , dx = \frac{x^{2+1}}{2+1} + C = \frac{x^3}{3} + C]

Таким образом, первообразная функции ( f(x) = x^2 ) равна:

[F(x) = \frac{x^3}{3} + C], где ( C ) – произвольная константа.

ChatGPT Online – AI Chat GPT

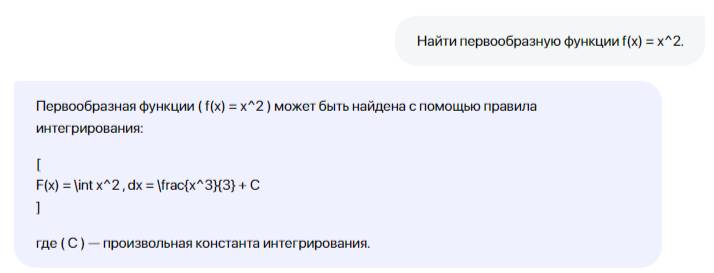
Нейросети GPTutor и GPT-4о правильно решили этот пример. Нейросеть ChatGPT ошиблась, перепутав делимое и делитель.

Но все три нейросети абсолютно правильно отметили очень важную особенность процесса нахождения первообразной, называемого интегрированием:

Если для данной функции f(x) существует первообразная, то она не является единственной.

Так, в примере 1 можно было взять в качестве первообразных следующие функции: F(x) = x^3/3 + 3; F(x) = x^3/3 + 13; F(x) = x^3/3 + 33 или вообще F(x) = x^3/3 + С, где С – произвольная постоянная (константа, как называют ее нейросети). Таки образом, если функция имеет первообразную, то она имеет их бесчисленное множество.

Все множество первообразных F(x) +C называется неопределенным интегралом от функции f(x) обозначается символом ∫f(x)dx.

При этом. функцию f(x)называют подынтегральной функцией, f(x)dx – подынтегральным выражением ,а знак ∫ – знаком интеграла.

Продолжим диалог с нейросетями.

Автор

Расскажите о свойствах интеграла.

Неросеть

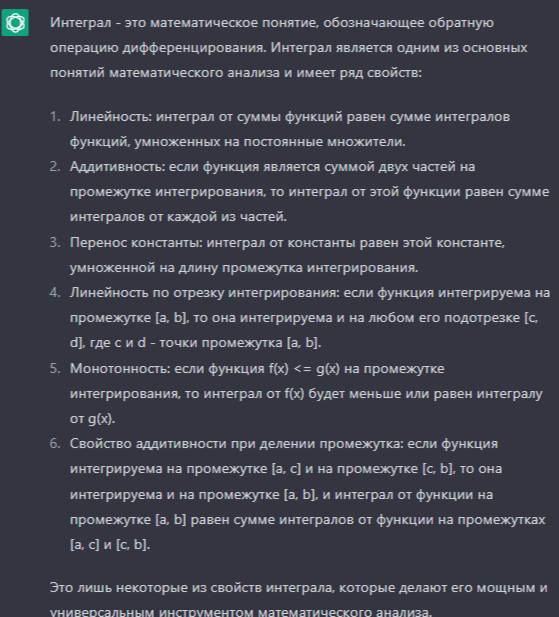
Автор

Расскажите о свойствах неопределенного интеграла.

Неросеть

1.2.Свойства неопределенного интеграла.

Неросеть

GPTutor

Неопределенный интеграл – это функция, которая показывает обобщение накопления (или суммы) значений некоторой функции. Основные свойства неопределенного интеграла включают:

Линейность:

[\int [a f(x) + b g(x)] , dx = a \int f(x) , dx + b \int g(x) , dx],

где (a) и (b) – константы, а (f(x)) и (g(x)) – функции.

Свойство постоянной функции:

[\int k , dx = kx + C].

где (k) – постоянная, а (C) – произвольная постоянная интегрирования.

Свойство замены переменной (подстановка):

Если (u = g(x)) – дифференцируемая функция, то:

[\int f(g(x)) g'(x) , dx = \int f(u) , du]

Свойство интегрирования по частям:

[\int u , dv = uv – \int v , du].

где (u) и (v) – функции, которые выбираются в зависимости от конкретной задачи.

Собственное значение интеграла:

Если (F(x)) – первообразная функции (f(x)) (то есть (F'(x) = f(x))), то:

[\int f(x) , dx = F(x) + C]

Интеграл по области:

Если (a < b), то:

[\int_a^b f(x) , dx = F(b) – F(a)].

где (F(x)) – первообразная функции (f(x)).

Эти свойства полезны для упрощения интегралов и решения интегральных уравнений. Если тебе нужны примеры или объяснения конкретных свойств, дай знать!

Автор

Таким образом:

II.Таблица интегралов

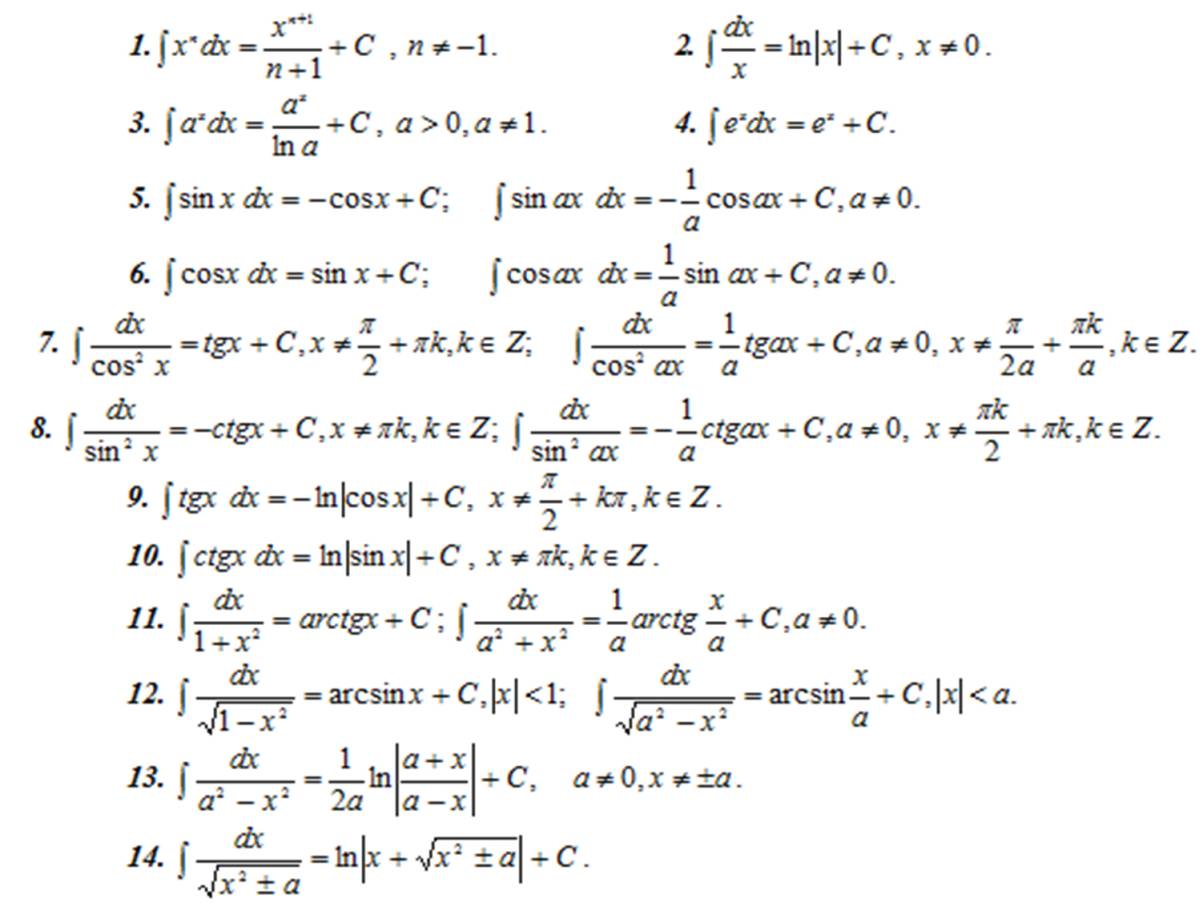
III.Методы интегрирования

3.1. С использованием таблицы интегралов.

Пример 2. Вычислить интеграл функции f(x) = x^2(1+2x)dx.

Попросим решить этот пример нейросеть:

GPTutor

Для вычисления интеграла функции ( f(x) = x^2(1 + 2x) ), начнем с раскрытия скобок:

[f(x) = x^2 + 2x^3.]

Теперь мы можем интегрировать каждое слагаемое по отдельности:

[\int f(x) , dx = \int (x^2 + 2x^3) , dx = \int x^2 , dx + \int 2x^3 , dx.]

Выполним интегрирование для каждого слагаемого:

(\int x^2 , dx = \frac{x^3}{3} + C_1),

(\int 2x^3 , dx = 2 \cdot \frac{x^4}{4} + C_2 = \frac{x^4}{2} + C_2).

Сложим результаты:

[\int f(x) , dx = \frac{x^3}{3} + \frac{x^4}{2} + C,]

где ( C = C_1 + C_2 ) – произвольная константа интегрирования.

Таким образом, окончательный ответ:

[\int x^2(1 + 2x) , dx = \frac{x^3}{3} + \frac{x^4}{2} + C.]

Ответ: (х^3)/3 + (x^4)/2 + C

Все правильно. Замечаний нет.

Пример 3.Вычислить интеграл функции f(x) = (5/x^(1/2) – x)dx.

GPTutor

Для вычисления интеграла функции ( f(x) = \left( \frac{5}{x^{1/2}} – x \right) ), мы можем записать его как:

[\int f(x) , dx = \int \left( \frac{5}{x^{1/2}} – x \right) , dx.]

Теперь разобьем интеграл на две части:

[\int f(x) , dx = \int \frac{5}{x^{1/2}} , dx – \int x , dx.]

Решим каждый из интегралов по отдельности:

Для первого интеграла:

[\int \frac{5}{x^{1/2}} , dx = 5 \int x^{-1/2} , dx = 5 \cdot \frac{x^{1/2}}{1/2} = 5 \cdot 2 x^{1/2} = 10 x^{1/2} = 10 \sqrt{x}.]

Для второго интеграла:

[\int x , dx = \frac{x^2}{2}.]

Теперь объединим результаты:

[\int f(x) , dx = 10 \sqrt{x} – \frac{x^2}{2} + C,]

где ( C ) – произвольная константа интегрирования.

Таким образом, окончательный ответ:

[\int \left( \frac{5}{x^{1/2}} – x \right) , dx = 10 \sqrt{x} – \frac{x^2}{2} + C.]

Ответ: 10*(х^1/2) – (x^2)/2 + C

Пример 4. Вычислить интеграл функции f(x) = (6x^2 + x – 1)dx.

Посмотрим, как с этим примером справится нейросеть GPTutor

Для вычисления интеграла функции ( f(x) = 6x^2 + x – 1 ) используем правила интегрирования.

Интеграл можно записать следующим образом:

[\int (6x^2 + x – 1) , dx = \int 6x^2 , dx + \int x , dx – \int 1 , dx]

Решая каждый интеграл по отдельности:

( \int 6x^2 , dx = 2x^3 + C_1 )

( \int x , dx = \frac{x^2}{2} + C_2 )

( \int 1 , dx = x + C_3 )

Складываем результаты:

[\int (6x^2 + x – 1) , dx = 2x^3 + \frac{x^2}{2} – x + C\]

где \( C = C_1 + C_2 – C_3 \) – произвольная константа интегрирования.

Итак, окончательный ответ:

\[\int (6x^2 + x – 1) \, dx = 2x^3 + \frac{x^2}{2} – x + C\].