Путешествие в квантовую механику

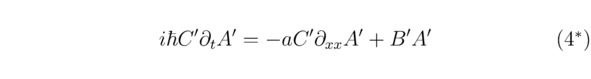
Примечательно, что в равенстве (4*) присутствуют общие экспоненциальные множители e-2iπ∞x/Rxe-2iπ∞x/Rx,…,e2iπmxx/Rxe2iπnxx/Rx,…,e2iπ∞x/Rxe2iπ∞x/Rx, от которых необходимо избавиться, оставив в результате только несокращаемые коэффициенты Фурье H`, H`` и H```. Теперь выполним несколько математических преобразований:

После чего разделим безразмерные переменные в уравнении (4``) относительно комплексного параметра Ψp (t, nx, mx), тогда:

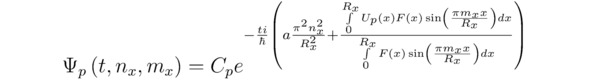
Напоследок, прибегая к тождеству ограниченности вероятности ∫-Rx0Rx0ΨΨ*dx=1, возьмём определённый интеграл ∫-Rx0Rx0ΨΨ*dx. В рассматриваемом примере подобранные коэффициенты Cp и Cp* не будут зависеть от времени t, поскольку сумма ∑p|Cp|2 останется постоянной ∑p|Cp|2=∑pCpCp*=1 в том случае, когда t=0 и/или все Ep∈R. Бесспорно, область определения действительной части волновой функции Re (Ψ) расположится на отрезке [0,Rx]. Вместе с тем для математической константы Rx возможно задать абсолютно любое положительное значение, удовлетворяющее равенству Rx=2Rx0/Ox. Неудивительно, что в рамках настоящей теории непрерывные выражения Ψ и Ψ* являются периодическими, а их графики y=Ψ (x) и y=Ψ* (x) симметричными или асимметричными относительно оси ординат y, следовательно:

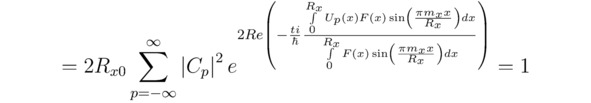
Наконец, отталкиваясь от выведенного ранее одномерного нестационарного линейного уравнения Шрёдингера, рассчитаем полную энергию Ep находящегося в состоянии Ψp электрона, тогда:

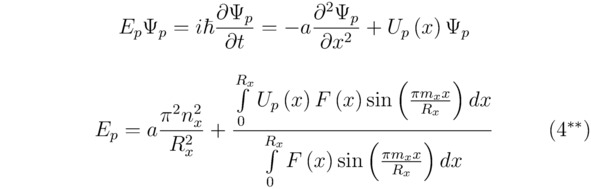
Для трёхмерного базиса (x,y,z) интересующая нас величина Ep составит:

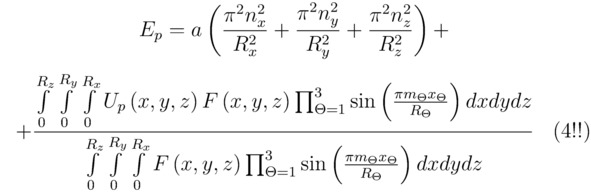
Если в формуле (4**), полученной для полной энергии Ep, произвольная функция F (x) не сократится, то найденный параметр Ep по факту окажется неопределённым (при Up (x) ≠const). Таким образом, опираясь на предложенную в данном параграфе методику, можно констатировать, что абсолютно все выраженные в общем виде соотношения E1, Ep и другие, похожие на эти, будут зависеть в том числе и от степени вариативности случайных процессов, протекающих в исследуемой физической системе. В стационарных условиях, когда Ep=const, левые и правые части тождеств (4**) и (4!!) примут фиксированные во времени t значения.

4.2 Кот Шрёдингера. Коллапс волновой функции

Если функции ψ1 и ψ2 являются волновыми, то их линейная суперпозиция ψ3 = c1ψ1 + c2ψ2 описывает некоторое состояние изолированной от внешнего воздействия квантовой системы. В том случае, когда измерение определённой физической величины f` в состоянии ψ1 приводит к результату f1, а в состоянии ψ2 – к результату f2, тогда измерение состояния ψ3 приведёт к результатам f1 или f2 с вероятностями |c1|2 и |c2|2 соответственно. Конечно, произвольно заданная комбинация частных аналитических решений того или иного нестационарного линейного уравнения Шрёдингера c1ψ1, c2ψ2, cpψp и всех оставшихся всегда может быть представлена как сумма эквивалентных им волновых функций ∑pΨp.

Совершенно ясно, что концепция мысленного эксперимента, связанного с котом Шрёдингера, заключается в следующей идее. Сперва в ящик помещаются банка с ядом, молоточный механизм с детектором и изначально живой кот. Естественно, что в ходе ядерной реакции срабатывает детектор, приводящий в движение разбивающий сосуд с ядом молоточный механизм, после чего кот умирает. Согласно квантовой механике, если над ядром не производится наблюдение, то его состояние описывается суперпозицией 2-х состояний: распавшегося и нераспавшегося. Между тем кот, сидящий в ящике, окажется и живым, и мёртвым одновременно. Если же ящик открыть, то экспериментатор сможет обнаружить только какое-нибудь одно конкретное состояние: «ядро распалось, кот мёртв» или «ядро не распалось, кот жив».

Немаловажно отметить, что в квантовой механике коллапс волновой функции Ψ возникает тогда и только тогда, когда обобщённая комплекснозначная величина Ψ (первоначально выраженная в виде суперпозиции нескольких собственных состояний Ψ=∑pΨp) сводится к одному собственному состоянию Ψp по причине взаимодействия изучаемой здесь физической системы с внешним миром. В дальнейшем это взаимодействие мы будем называть «наблюдением» или «измерением». Под нормированной суперпозицией ∫-Rx0Rx0ΨΨ*dx=1 понимается приравненная к единице сумма проинтегрированных по dx надлежащих плотностей вероятностей ∑p∫-Rx0Rx0ΨpΨp*dx=1, которые допустимо считать взаимно зависимыми. Безусловно, всякая объединённая волновая функция ∑pΨp, несмотря ни на какие обстоятельства, будет продолжать подчиняться тому или иному линейному нестационарному уравнению Шрёдингера, точно так же как и сама величина Ψp.

В 1927 году Вернер Гейзенберг использовал идею редукции волновой функции ψ для объяснения квантового измерения искомой нормированной вероятности |cp|2. Однако в этом параграфе будет показано, что коллапс – это фундаментальное физическое явление, которое возможно обосновать математически, опираясь на общее аналитическое решение того или иного нестационарного линейного уравнения Шрёдингера Ψ. Кстати говоря, сами вычисления нужно производить в трёхмерном комплексном пространстве. Тем не менее для упрощения расчётов мы выберем одномерный случай. Пусть F (x) =d (x) +ib (x), следовательно:

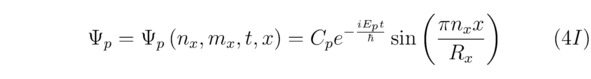
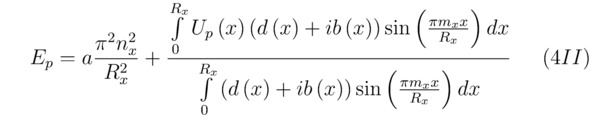
Несомненно, квадрат модуля коэффициента |Cp|2 будет определять начальную нормированную вероятность |cp|2 локализации соответствующей частицы в состоянии ψp. Действительно, постоянный член aπ2nx2/Rx2, входящий в состав формулы (4II), всегда можно опустить, поскольку выше было положено условие зависимости полной энергии Ep от произвольно заданной функции F (x). Для того чтобы осуществить дальнейшие математические преобразования, необходимо в первую очередь выделить вещественную часть Re (iEp) из отыщенного ранее выражения (4II). Допустим, что E*p=Re (-iEp), тогда:

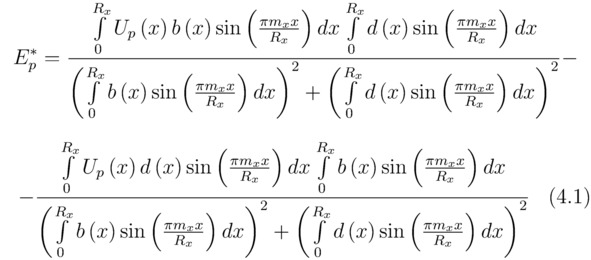
Суперпозицию квантовых состояний Ψ=∑p=1S`Ψp удобно представить так:

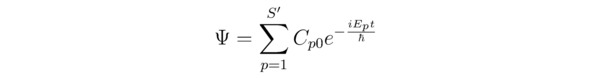
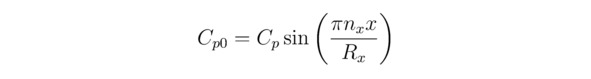
где S` – полное количество возможных состояний изучаемой в данный момент физической системы C10