
Полная версия
Нейросети. Обработка аудиоданных
signal = np.sin(2 * np.pi * frequency * t)
# Выполняем Преобразование Фурье
fft_result = np.fft.fft(signal)
freqs = np.fft.fftfreq(len(fft_result), 1 / sample_rate) # Частоты
# Визуализируем спектральное представление
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.plot(t, signal)
plt.title('Временное представление аудиосигнала')
plt.xlabel('Время (с)')
plt.ylabel('Амплитуда')
plt.subplot(122)
plt.plot(freqs, np.abs(fft_result))
plt.title('Спектральное представление аудиосигнала')
plt.xlabel('Частота (Гц)')
plt.ylabel('Амплитуда')
plt.xlim(0, 20) # Ограничиваем частотный диапазон
plt.show()
```
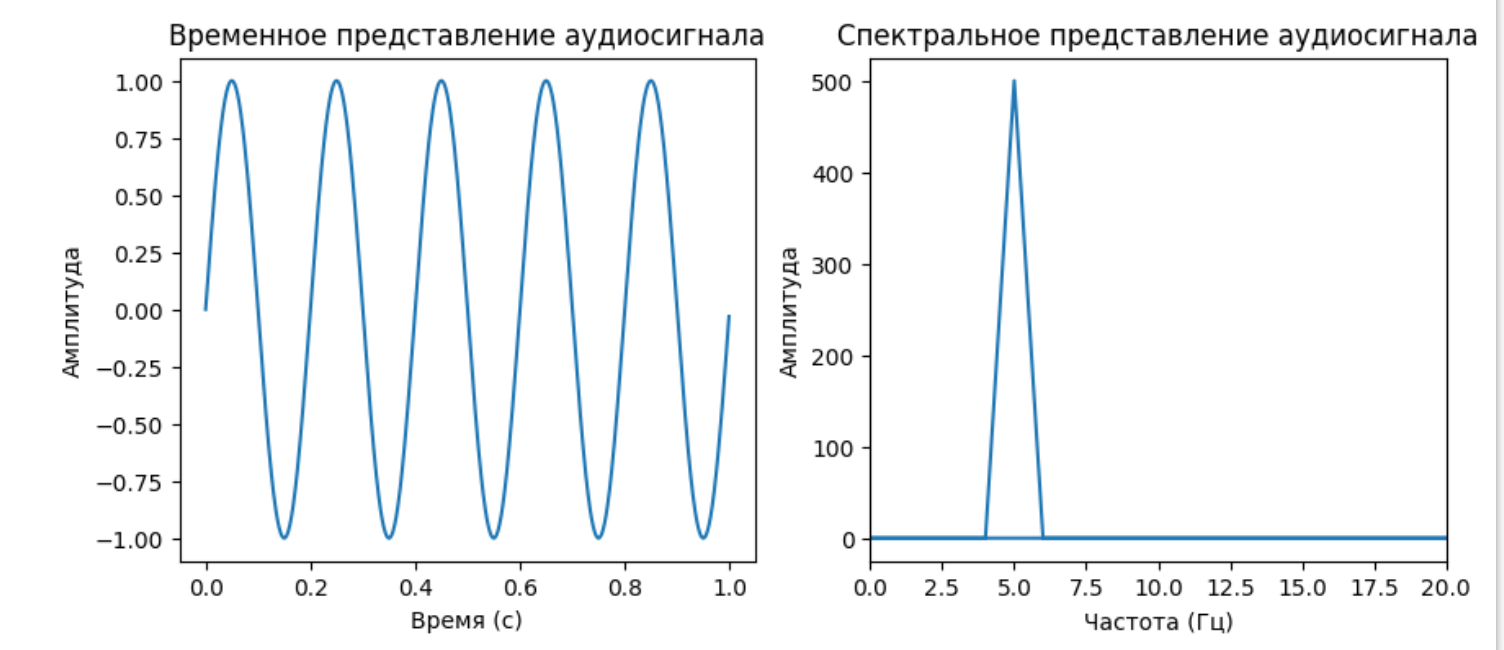
В этом примере мы создаем синусоидальный аудиосигнал, выполняем Преобразование Фурье для анализа его спектральных компонент, и визуализируем результаты. Первый график показывает временное представление сигнала, а второй график показывает спектральное представление, выделяя основную частоту синусоиды.
Вы можете экспериментировать с различными сигналами и частотами, чтобы лучше понять, как Преобразование Фурье позволяет анализировать аудиосигналы в
Преобразование Фурье в аудиотехнологиях:
В аудиотехнологиях часто используется быстрое преобразование Фурье (FFT), что позволяет эффективно вычислять спектр аудиосигнала в реальном времени. Оно является основой для многих алгоритмов аудиообработки, таких как эквалайзеры, компрессоры, реверберации и другие аудиоэффекты.
Преобразование Фурье играет важную роль в анализе и обработке аудиосигналов, обеспечивая возможность изучать и манипулировать спектральными характеристиками звуковых записей и создавать разнообразные аудиоэффекты.
Вейвлет-преобразование – это более продвинутый метод, который позволяет анализировать аудиосигналы на разных временных и частотных масштабах. Вейвлет-преобразование разлагает сигнал, используя вейвлет-функции, которые могут быть масштабированы и сдвинуты. Это позволяет выделять как быстрые, так и медленные изменения в сигнале, что особенно полезно при анализе звука с переменной частотой и интенсивностью.
Концепция Вейвлет-преобразования включает в себя несколько шагов, которые позволяют анализировать аудиосигналы на различных временных и частотных масштабах. Рассмотрим эти шаги более подробно:
1. Выбор вейвлета: Первым шагом является выбор подходящего вейвлета. Вейвлет – это специальная функция, которая используется для разложения сигнала. Разные вейвлеты могут быть более или менее подходящими для различных типов сигналов. Например, вейвлет Добеши (Daubechies) часто используется в аудиообработке.

2. Разложение сигнала: Сигнал разлагается на вейвлет-коэффициенты, используя выбранный вейвлет. Этот шаг включает в себя свертку сигнала с вейвлет-функцией и вычисление коэффициентов на разных масштабах и позициях во времени.

3. Выбор временных и частотных масштабов: Вейвлет-преобразование позволяет анализировать сигнал на различных временных и частотных масштабах. Это достигается за счет масштабирования и сдвига вейвлет-функции. Выбор конкретных масштабов зависит от задачи анализа.
4. Интерпретация коэффициентов: Полученные вейвлет-коэффициенты представляют собой информацию о том, какие временные и частотные компоненты присутствуют в сигнале. Это позволяет анализировать изменения в сигнале на разных временных и частотных масштабах.
5. Визуализация и интерпретация: Результаты Вейвлет-преобразования могут быть визуализированы, например, в виде спектрограммы вейвлет-коэффициентов. Это позволяет аналитику или исследователю видеть, какие частоты и временные изменения доминируют в сигнале.
Пример на Python для анализа аудиосигнала с использованием библиотеки PyWavelets:
```python
import pywt
import pywt.data
import numpy as np
import matplotlib.pyplot as plt
# Создаем пример аудиосигнала
signal = np.sin(2 * np.pi * np.linspace(0, 1, 1000))
# Выполняем Вейвлет-преобразование
coeffs = pywt.wavedec(signal, 'db1', level=5)
# Визуализируем результат
plt.figure(figsize=(12, 4))
plt.subplot(121)
plt.plot(signal)
plt.title('Исходный аудиосигнал')
plt.subplot(122)
plt.plot(coeffs[0]) # Детализирующие коэффициенты
plt.title('Вейвлет-коэффициенты')
plt.show()
```
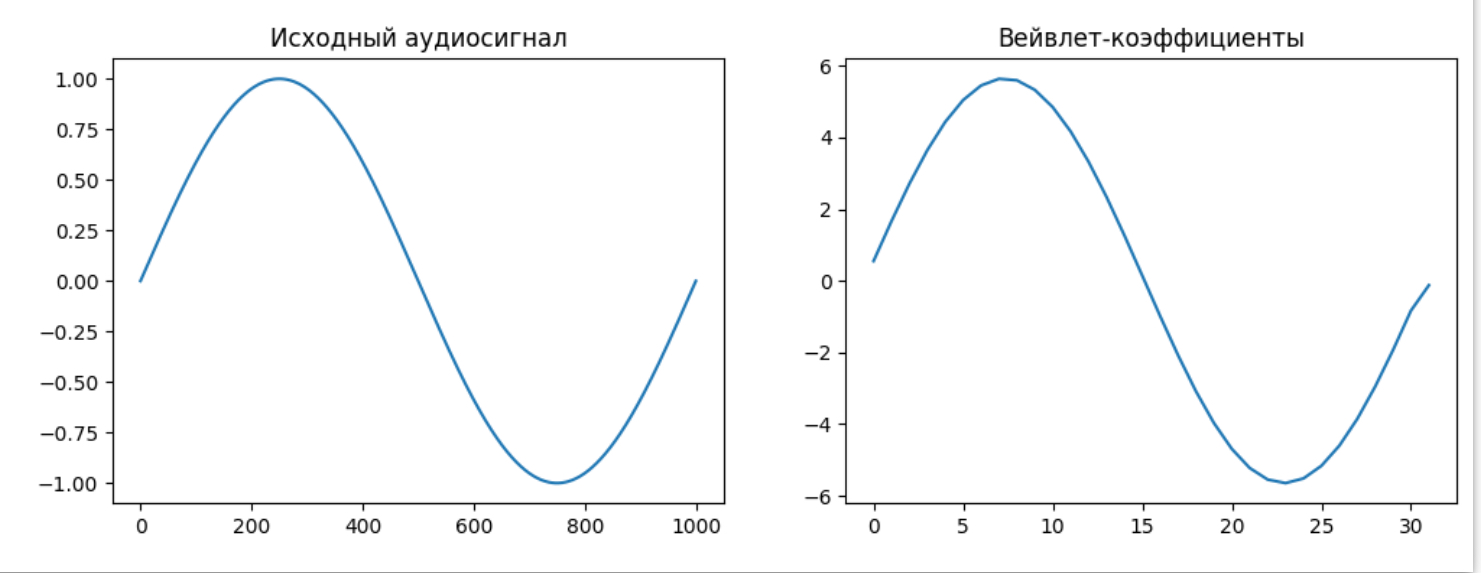
В этом примере мы создаем простой синусоидальный аудиосигнал и выполняем Вейвлет-преобразование, используя вейвлет Добеши первого уровня. Полученные коэффициенты представляют информацию о различных временных и частотных компонентах сигнала.
Используя Вейвлет-преобразование, вы можете анализировать аудиосигналы на различных временных и частотных масштабах, что делает его мощным инструментом в аудиообработке и анализе звука.
Оба метода, преобразование Фурье и вейвлет-преобразование, имеют свои собственные преимущества и применения. Преобразование Фурье обеспечивает хороший спектральный анализ и используется в задачах, таких как эквалайзинг и анализ спектра. Вейвлет-преобразование более гибкое и позволяет анализировать сигналы с разной временной и частотной структурой, что полезно в аудиоинженерии и обнаружении аномалий.
В зависимости от конкретной задачи и требований анализа аудиосигнала, один из этих методов может быть более предпочтителен.
Глава 3: Основы нейросетей и глубокого обучения
3.1. Обзор архитектур нейросетей, включая сверточные и рекуррентные нейронные сети
Обзор архитектур нейронных сетей включает в себя разнообразные архитектуры, разработанные для решения различных задач машинного обучения. Среди них особенно выделяются сверточные и рекуррентные нейронные сети.
Сверточные нейронные сети (Convolutional Neural Networks, CNN)
Основное применение: Обработка изображений и видео, распознавание объектов, классификация и сегментация изображений.
Основные элементы: Сверточные слои, пулинг слои и полносвязные слои.
Принцип работы: Сверточные нейронные сети (CNN) – это специализированный вид нейронных сетей, разработанный для обработки изображений и других данных с сетчатой структурой, таких как видео или звук. Основной принцип работы CNN заключается в использовании сверточных слоев для извлечения признаков и пулинг слоев для уменьшения размерности данных.
Сверточные слои работают с помощью ядер свертки, которые скользят по входным данным и вычисляют взвешенную сумму значений в заданной области. Это позволяет выделить локальные шаблоны и структуры в данных, создавая карты признаков. После свертки применяется функция активации, обычно ReLU, чтобы внедрить нелинейность в модель.
Пулинг слои применяются после сверточных слоев и служат для уменьшения размерности карт признаков. Это повышает эффективность работы сети и сокращает количество параметров. Операции пулинга могут быть максимальными (Max Pooling) или средними (Average Pooling), и они выполняются на каждом канале и в каждой области данных. Совместное использование сверточных и пулинг слоев позволяет CNN автоматически извлекать важные признаки на разных уровнях абстракции, что делает их мощными инструментами для обработки изображений и других структурированных данных.
2. Рекуррентные нейронные сети (Recurrent Neural Networks, RNN)
Основное применение: Обработка последовательных данных, таких как текст, речь, временные ряды.
Основные элементы: Рекуррентные слои, включая LSTM (Long Short-Term Memory) и GRU (Gated Recurrent Unit).
Принцип работы: Рекуррентные нейронные сети (RNN) представляют собой класс нейронных сетей, специально разработанных для работы с последовательными данных, такими как текст, речь, временные ряды и другие. Принцип работы рекуррентных слоев в RNN заключается в том, что они обладают памятью и способностью учитывать предыдущее состояние при обработке текущего входа, что делает их идеальными для моделирования зависимостей и контекста в последовательных данных.
Рекуррентный слой обрабатывает входные данные поэлементно, и каждый элемент (например, слово в предложении или отсчет временного ряда) обрабатывается с учетом предыдущего состояния. Это позволяет сети учитывать и использовать информацию из прошлого при анализе текущей части последовательности.
Основные архитектуры рекуррентных слоев включают в себя стандартные RNN, LSTM (Long Short-Term Memory) и GRU (Gated Recurrent Unit). LSTM и GRU являются более продвинутыми версиями рекуррентных слоев и решают проблему затухания и взрыва градиентов, что часто встречается при обучении стандартных RNN.
Преимущество RNN заключается в их способности захватывать долгосрочные зависимости в данных и моделировать контекст. Они применяются в задачах машинного перевода, анализа текста, генерации текста, распознавания речи и других задачах, где важен анализ последовательных данных. Однако они также имеют свои ограничения, такие как ограниченная параллельность в обучении, что привело к разработке более сложных архитектур, таких как сверточные рекуррентные сети (CRNN) и трансформеры, которые спроектированы для более эффективной обработки последовательных данных в контексте современных задач машинного обучения.
3. Сети с долгой краткосрочной памятью (LSTM)
Особенности: Люди часто взаимодействуют с данными, обладая долгосрочной памятью, которая позволяет им запоминать и учитывать информацию, полученную на протяжении длительных временных интервалов. Рекуррентные нейронные сети (RNN) были разработаны для моделирования подобного поведения, но стандартные RNN имеют ограничения в способности улавливать долгосрочные зависимости в данных из-за проблемы затухания градиентов.
В ответ на это ограничение были созданы сети долгой краткосрочной памяти (LSTM). LSTM представляют собой особый тип рекуррентных нейронных сетей, которые обладают способностью эффективно улавливать долгосрочные зависимости в данных благодаря механизмам забывания и хранения информации в памяти.
Основные черты LSTM включают в себя:
Механизм забывания: LSTM обладают специальным механизмом, который позволяет им забывать ненужные информации и сохранять важные. Это механизм помогает устранить проблему затухания градиентов, позволяя сети сохранять и обновлять состояние памяти на протяжении длительных последовательностей данных.
Хранение долгосрочных зависимостей: LSTM способны запоминать информацию на долгосрочный период, что делает их подходящими для задач, где важны долгосрочные зависимости, такие как обработка текстовых последовательностей и анализ временных рядов.
Универсальность: LSTM могут использоваться в различных областях, включая обработку естественного языка, генерацию текста, распознавание речи, управление временными рядами и многое другое. Их уникальная способность к моделированию долгосрочных зависимостей делает их неотъемлемой частью современных задач машинного обучения.
С использованием механизмов LSTM, нейронные сети способны учитывать более сложные и долгосрочные зависимости в данных, что делает их мощными инструментами для моделирования и предсказания в различных областях и задачах.
4. Сети с управляемой памятью (Memory Networks)
Особенности: Сети долгой краткосрочной памяти с внешней памятью (LSTM с External Memory) представляют собой продвинутую версию рекуррентных нейронных сетей (LSTM), которые обладают уникальной способностью моделировать и взаимодействовать с внешней памятью. Это делает их идеальными для задач, связанных с обработкой текстовой информации и вопрос-ответ.
Особенности таких сетей включают в себя:
Внешняя память: LSTM с External Memory обладают дополнительной памятью, которую они могут читать и записывать. Эта внешняя память позволяет им хранить информацию, необходимую для решения сложных задач, где контекст и взаимосвязь между разными частями текста играют важную роль.
Обработка текста и вопрос-ответ: Благодаря способности взаимодействия с внешней памятью, LSTM с External Memory могут успешно решать задачи вопрос-ответ, где необходимо анализировать текстовые вопросы и извлекать информацию из текстовых источников, чтобы предоставить информативные ответы.
Моделирование сложных зависимостей: Эти сети способны моделировать сложные и долгосрочные зависимости в текстовых данных, что делает их идеальными для задач, таких как машинный перевод, анализ текста и анализ тональности, где важна интерпретация и понимание контекста.
Сети LSTM с External Memory представляют собой мощный инструмент для обработки текстовой информации и вопросов, что делает их полезными в таких приложениях, как чат-боты, виртуальные ассистенты, поисковые системы и многие другие задачи, где требуется анализ и взаимодействие с текстовыми данными. Эти сети позволяют моделировать более сложные и информативные зависимости в тексте, что делает их незаменимыми в задачах обработки текстовой информации.
5. Сети глубокого обучения (Deep Learning)
Особенности: Глубокие нейронные сети (Deep Neural Networks, DNNs) представляют собой класс мощных моделей, характеризующихся большим количеством слоев, что делает их способными автоматически извлекать сложные и абстрактные признаки из данных. Это их главная особенность, которая сделала их важными инструментами в области машинного обучения и искусственного интеллекта.
Особенности глубоких нейронных сетей включают:
Глубокая структура: DNNs включают множество слоев, составляющих структуру модели. Эти слои образуют цепочку, где каждый слой обрабатывает данные на разных уровнях абстракции. Благодаря большому количеству слоев, сети могут автоматически извлекать признаки на разных уровнях сложности.
Автоматическое извлечение признаков: Одной из ключевых сил глубоких нейронных сетей является их способность автоматически извлекать признаки из данных. Например, в обработке изображений они могут выявлять края, текстуры, объекты и даже абстрактные концепции, не требуя ручного создания признаков.
Применение в различных областях: Глубокие нейронные сети нашли применение в различных областях машинного обучения, включая обработку изображений, аудиоанализ, обработку текста, генеративное моделирование и многие другие. Они использовались для создания передовых систем распознавания объектов, автономных автомобилей, систем распознавания речи, а также в нейронном машинном переводе и виртуальной реальности.
Глубокие нейронные сети, включая такие архитектуры как сверточные нейронные сети (CNNs) и рекуррентные нейронные сети (RNNs), представляют собой ключевой компонент современных искусственных интеллектуальных систем. Их способность автоматически извлекать сложные признаки из данных и решать разнообразные задачи делает их незаменимыми инструментами в множестве приложений, где необходим анализ и обработка данных.
6. Сети автокодировщиков (Autoencoders)
Особенности: Сети автокодировщиков (Autoencoders) представляют собой класс нейронных сетей, который призван решать задачу обучения компактных представлений данных. Основными особенностями автокодировщиков являются их способность сжимать и кодировать данные, а также восстанавливать исходные данные с минимальными потерями информации. Архитектура автокодировщиков состоит из двух основных компонентов: кодировщика и декодировщика.
Кодировщик (Encoder): Кодировщик принимает на вход данные и преобразует их в более компактное представление, называемое кодом или латентным представлением. Это сжатое представление содержит наиболее важные признаки и характеристики данных. Кодировщик обучается извлекать эти признаки автоматически, что позволяет сократить размерность данных.
Декодировщик (Decoder): Декодировщик выполняет обратную операцию. Он принимает код или латентное представление и восстанавливает исходные данные из него. Это восстановление происходит с минимальными потерями информации, и задача декодировщика – максимально приблизить восстановленные данные к исходным.
Процесс обучения автокодировщика заключается в минимизации разницы между входными данными и восстановленными данными. Это требует оптимального кодирования информации, чтобы она могла быть успешно восстановлена из латентного представления. В результате, автокодировщики выучивают компактные и информативные представления данных, которые могут быть полезными в различных задачах, таких как снижение размерности данных, извлечение признаков, а также визуализация и генерация данных.
Автокодировщики также имеют множество вариаций и применяются в различных областях машинного обучения, включая анализ изображений, обработку текста и рекомендательные системы. Эти сети представляют собой мощный инструмент для извлечения и представления информации в данных в более компактной и удобной форме.
7. Сети генеративных адверсариальных сетей (GANs)
Основное применение: Создание и модификация данных, генерация изображений, видео, музыки и других медиа-контента.
Особенности: GANs включают генератор и дискриминатор, которые соревнуются между собой. Это позволяет создавать новые данные, неотличимые от реальных.
Сети генеративных адверсариальных сетей (GANs) представляют собой инновационный и мощный класс нейронных сетей, разработанный для задач генерации данных. Одной из ключевых особенностей GANs является их структура, состоящая из двух основных компонентов: генератора и дискриминатора. Эти две сети соревнуются между собой в процессе обучения, что позволяет создавать новые данные, которые могут быть практически неотличимы от реальных.
Генератор (Generator): Главная задача генератора в GANs заключается в создании данных, которые максимально похожи на настоящие. Генератор принимает на вход случайный шумовой вектор и постепенно преобразует его в данные, которые он создает. В процессе обучения генератор стремится создавать данные так, чтобы они обманывали дискриминатор и были классифицированы как реальные.
Дискриминатор (Discriminator): Дискриминатор является второй важной частью GANs. Его задача – отличать сгенерированные данные от настоящих данных. Дискриминатор принимает на вход как сгенерированные данные от генератора, так и настоящие данные, и старается правильно классифицировать их. В процессе обучения дискриминатор улучшает свои способности различать поддельные и реальные данные.
Соревнование между генератором и дискриминатором: Важной особенностью GANs является их обучение через игру. Генератор и дискриминатор соревнуются друг с другом: генератор старается создавать данные, которые обманут дискриминатор, а дискриминатор старается лучше различать сгенерированные данные от реальных. Этот процесс итеративно повышает качество сгенерированных данных, и с течением времени генератор становится все более и более умелым в создании данных, неотличимых от реальных.
GANs нашли применение в различных областях, включая генерацию изображений, видео, музыки, текста и многих других типов данных. Они также используются для усовершенствования существующих данных и для создания аугментированных данных для обучения моделей машинного обучения. Эти сети представляют собой мощный инструмент для генерации и модификации данных, и их потенциал в мире искусственного интеллекта продолжает расти.
8. Сети долгой краткосрочной памяти с вниманием (LSTM с Attention)
Особенности: Сети с долгой краткосрочной памятью с вниманием (LSTM с Attention) представляют собой эволюцию рекуррентных нейронных сетей (LSTM), которые дополняются механизмами внимания. Они обладают уникальными особенностями, которые делают их мощными для обработки последовательных данных, таких как текст и речь.
Основной элемент сетей LSTM с вниманием – это LSTM, которые предоставляют сети возможность учитывать долгосрочные зависимости в данных и сохранять информацию в долгосрочной и краткосрочной памяти. Важно, что они также способны учитывать предыдущее состояние при анализе текущего входа.
Однако основной силой сетей LSTM с вниманием является механизм внимания. Этот механизм позволяет модели определять, на какие части входных данных следует обратить особое внимание, присваивая различные веса элементам последовательности. Благодаря этому, сеть способна фокусироваться на наиболее важных частях данных, улучшая анализ контекста и зависимостей в последовательных данных. Это делает сети LSTM с вниманием весьма эффективными инструментами для задач обработки естественного языка, машинного перевода и других задач, где понимание контекста играет важную роль.
Это небольшой обзор различных типов архитектур нейронных сетей. Каждая из них имеет свои преимущества и недостатки и может быть настроена для конкретной задачи машинного обучения.
3.2. Обучение нейросетей и выбор оптимальных функций потерь
Обучение нейронных сетей – это процесс, в ходе которого сеть настраивается на определенную задачу путем адаптации своих весов и параметров. Важной частью этого процесса является выбор и оптимизация функции потерь (loss function), которая измеряет разницу между предсказаниями модели и фактическими данными. Выбор оптимальной функции потерь зависит от конкретной задачи машинного обучения, и разные функции потерь применяются в разных сценариях. В этом разделе рассмотрим основы обучения нейросетей и рассмотрим выбор функций потерь.
Процесс обучения нейронной сети:
1. Подготовка данных: Перед началом обучения нейросети данные должны быть правильно подготовлены. Это включает в себя предобработку данных, такую как масштабирование, нормализацию и кодирование категориальных переменных. Данные также разделяются на обучающий, валидационный и тестовый наборы.
2. Выбор архитектуры сети: В зависимости от задачи выбирается архитектура нейросети, включая количество слоев, количество нейронов в каждом слое и типы слоев (например, сверточные, рекуррентные и полносвязанные).
3. Определение функции потерь: Функция потерь является ключевой частью обучения. Она измеряет разницу между предсказаниями модели и фактическими данными. Выбор правильной функции потерь зависит от задачи: для задачи регрессии часто используется среднеквадратичная ошибка (MSE), а для задачи классификации – кросс-энтропия.
4. Оптимизация: Для настройки параметров сети минимизируется функция потерь. Это делается с использованием методов оптимизации, таких как стохастический градиентный спуск (SGD) или его варианты, включая Adam и RMSprop.
5. Обучение и валидация: Нейронная сеть обучается на обучающем наборе данных, и ее производительность оценивается на валидационном наборе данных. Это позволяет отслеживать процесс обучения и избегать переобучения.
6. Тестирование: После завершения обучения сети ее производительность проверяется на тестовом наборе данных, чтобы оценить ее способность к обобщению.
Выбор оптимальной функции потерь
Выбор функции потерь зависит от конкретной задачи машинного обучения. Рассмотрим распространенные функции потерь:
–
Среднеквадратичная ошибка
(MSE
):
Используется в задачах регрессии для измерения средней квадратичной разницы между предсказанными и фактическими значениями
.
Среднеквадратичная ошибка (Mean Squared Error, MSE) – это одна из наиболее распространенных и широко используемых функций потерь в задачах регрессии в машинном обучении. Ее основное назначение – измерять среднюю квадратичную разницу между предсказанными значениями модели и фактическими значениями в данных. MSE является метрикой, которая позволяет оценить, насколько хорошо модель соответствует данным, и какие ошибки она допускает в своих предсказаниях.
Принцип работы MSE заключается в следующем:
1. Для каждого примера в обучающем наборе данных модель делает предсказание. Это предсказание может быть числовым значением, таким как цена дома или температура, и модель пытается предсказать это значение на основе входных признаков.
2. Разница между предсказанным значением и фактическим значением (истинным ответом) для каждого примера вычисляется. Эта разница называется "остатком" или "ошибкой" и может быть положительной или отрицательной.









