Альтернативный волновой анализ. Новые горизонты

Валерий Борискин

Альтернативный волновой анализ. Новые горизонты

Введение

Материал, изложенный в этой книге, представляет собой дальнейшее развитие идей, рассмотренных мною в предыдущей книге «Альтернативный волновой анализ».

Базисом теории является предположение о том, что в основе развития ценового графика любого финансового инструмента лежит геометрический фрактал – дерево Пифагора (Мировое Древо). Ну или, если говорить точнее, его основа – Пифагоровы штаны, которые, как известно, во все стороны равны. Отсюда, кстати, и симметрия.

Так вот, ключевая идея заключается в том, что по мере развития (усложнения структуры) ценового дерева путем вычислений мы можем точно зафиксировать только те моменты, когда происходит выполнение условия равенства площадей на разных уровнях детализации фрактальной модели – дерева Пифагора. Это и есть циклы.

Именно в эти моменты на рынке возникает симметрия. Но симметрия не временная, а структурная (событийная). Симметрия, выраженная в равенстве площадей.

Именно в эти мгновения образуется циклы, которые рассматриваются затем как стоячие волны ценовых графиков, создающие устойчивую интерференционную картину распределения минимумов и максимумов.

Дальнейшее развитие теории уводит нас к такому фундаментальному физическому явлению, как интерференция волн.

Дело в том, что любая волновая модель в альтернативном волновом анализе рассматривается в качестве источника (центра) возмущения (излучения), порождающего когерентные волны, а результирующее поле в каждой точке ценового графика определяется интерференцией этих волн.

Таким образом, получается, что выделение волновых циклов в AWA является не чем иным, как анализом интерференционной картины ценового графика, которая постоянно меняется по мере появления все новых и новых источников когерентных волн (фрактальных элементов), то есть новых волновых моделей.

Теория

Различия между EWA и AWA

На сегодняшний день среди тех, кто использует в торговле на финансовых рынках волновой анализ, наиболее известной и чаще всего применяемой является классическая теория волн Эллиотта.

Поэтому книгу я решил начать с перечисления основных различий между теорией волн Эллиотта (EWA) и альтернативным волновым анализом (AWA).

Итак, в качестве постулатов AWA использованы следующие утверждения:

При этом базисом альтернативного волнового анализа является предположение о том, что в основе развития ценового графика финансового инструмента лежит геометрический фрактал – дерево Пифагора (Мировое Древо).

Ну или, если говорить точнее, его основа – Пифагоровы штаны, которые, как известно, во все стороны равны.

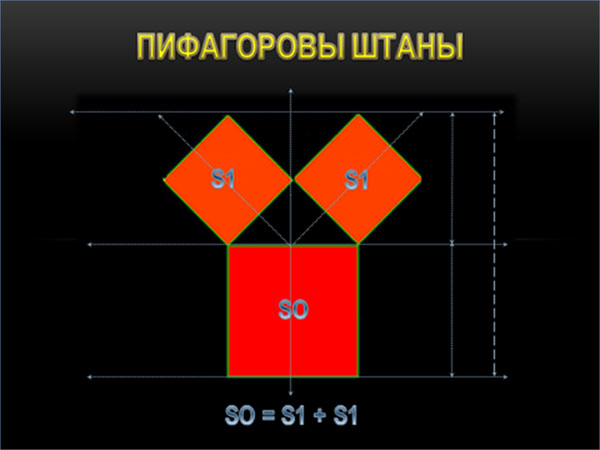
Так вот, ключевая идея альтернативного волнового анализа заключается в том, что по мере развития (усложнения структуры) ценового дерева путем вычислений мы можем точно зафиксировать только те моменты, когда происходит выполнение условия равенства площадей на разных уровнях детализации дерева Пифагора. Это и есть циклы.

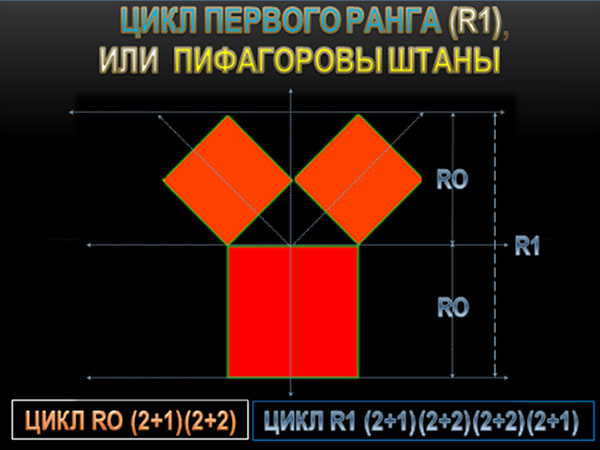
Именно в эти моменты на рынке и происходит возникновении симметрии. Но симметрии не временной, а структурной (событийной), симметрии, выраженной в равенстве площадей.

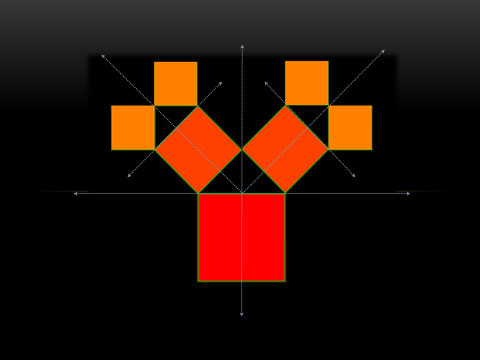
Однако AWA не может прогнозировать, когда именно возникнет новый цикл, так как последовательность формирования структуры ценового дерева является по своей сути процессом хаотическим, а значит, практически не поддающимся прогнозированию.

Но, несмотря на непредсказуемый процесс формирования дерева (цены), который можно сравнить со сборкой пазла, когда мы случайным образом достаем из набора все новые и новые элементы дерева, тем не менее, площади самих фигур вычислить мы можем.

Путем расчетов у нас всегда получится определить те ключевые моменты, когда происходит выполнение условия равенства площадей для различных уровней детализации нашей фрактальной модели.

Именно эти точки и можно считать моментами возникновения симметрии. Именно в эти мгновения образуются циклы, которые рассматриваются затем как стоячие волны ценовых графиков, создающие устойчивую интерференционную картину распределения минимумов и максимумов.

При этом, в отличие от EWA, где используется 2 разновидности волновых конструкций (пятиволновка и ABC-зигзаг), в AWA используется 3 вида волновых конструкций. Условно: S-пятиволновка (±2), X-зигзаг (±2) и антиX-зигзаг (±1).

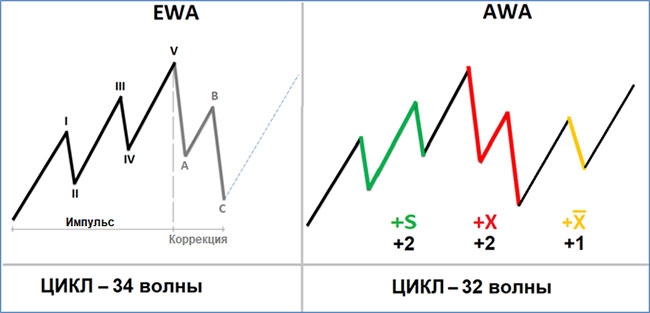
При этом AWA опирается на гармонический 32-волновой цикл, а не на классический 34-волновой цикл Эллиотта.

Более того, в альтернативном волновом анализе базовые эллиоттовские пятиволновка и ABC-зигзаг являются всего лишь разновидностями одной, общей для всех четной и полностью симметричной N-модели, представляя собой различные ее искажения вдоль спирали.

Поэтому если мы рассмотрим все возможные комбинации таких разновидностей, то обнаружим, что их может быть всего 8 (23). Отсюда и возник алфавит альтернативного волнового анализа – NASH FLEX.

Однако все модели из алфавита NASH FLEX – это только четные конструкции с параметром ±2. Но у нас есть еще нечетная модель антиX с параметром ±1.

Поэтому полная схема волновых формаций будет выглядеть следующим образом:

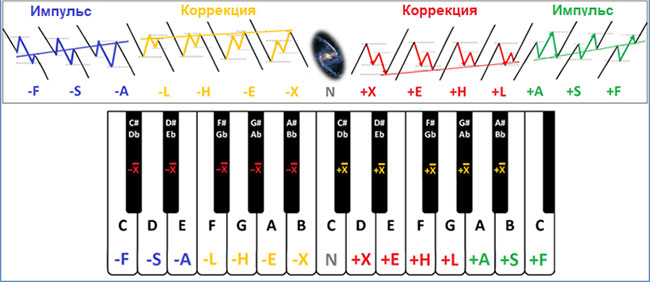
Все 8 четных моделей NASH FLEX плюс 1 нечетная модель антиX хорошо укладываются в 2 октавы, а сами волновые модели, по сути, представляют собой различные ноты.

Таким образом, AWA позволяет не только фиксировать волновые модели, но и записывать ценовой график в виде последовательности нот. Дальнейшее развитие теории уводит нас к такому фундаментальному физическому явлению, как интерференция волн.

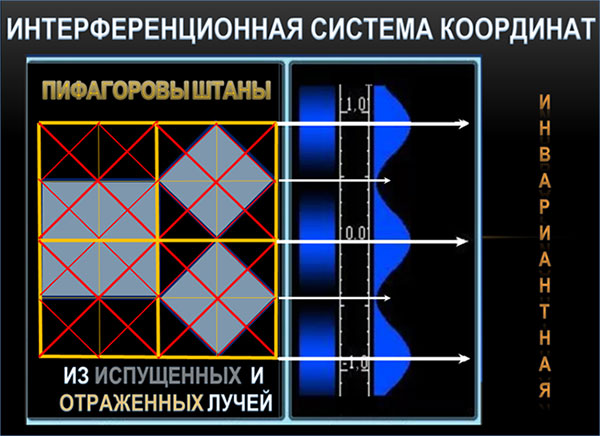
Дело в том, что любая волновая модель в альтернативном волновом анализе рассматривается в качестве источника (центра) возмущения (излучения), порождающего когерентные волны, а результирующее поле в каждой точке ценового графика определяется интерференцией этих волн.

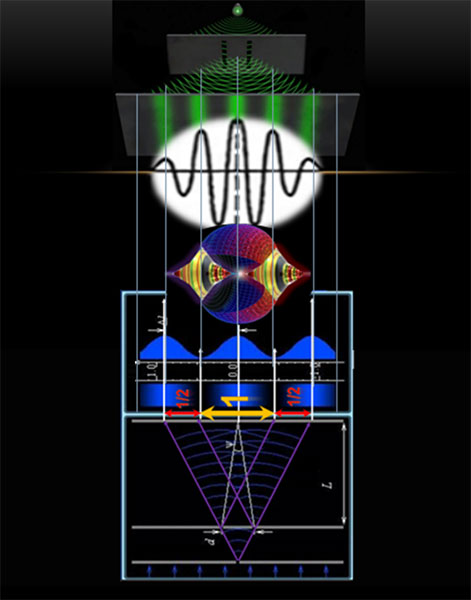
Таким образом, получается, что выделение волновых циклов в AWA является не чем иным, как анализом интерференционной картины, которая постоянно меняется по мере появления все новых и новых источников когерентных волн – волновых моделей.

Теперь становится понятным, почему играет большую роль понятие четности и нечетности моделей, пар и т. д.

Дело в том, что согласно классической физической теории:

• интерференционные минимумы возникают тогда, когда разность хода между источниками равна нечетному количеству полуволн;

• интерференционные максимумы образуются тогда, когда разность хода между источниками равна четному количеству полуволн.

Так определяется, сформирован ли сейчас узел или пучность стоячей волны.

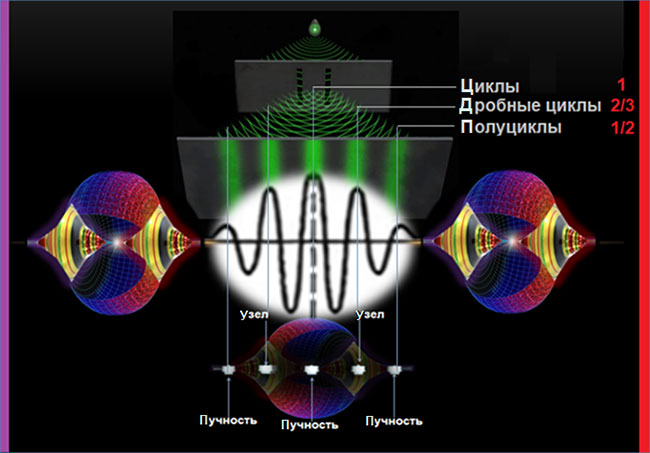
Циклы, полуциклы и дробные циклы

Циклы, полуциклы и дробные циклы являются главными комбинациями в альтернативном волновом анализе. Все они представляют собой различные резонансы и формируют своеобразные преграды на пути движения потока, которые ему необходимо преодолеть, чтобы у него была возможность двигаться далее.

Но давайте по порядку.

Четвертый постулат AWA гласит: все волновые модели (пакеты) должны повторить друг друга (создать пару). Под созданием пары подразумевается объединение двух последовательных волновых моделей.

Кроме волновых моделей из алфавита (NASH FLEX), которые являются четными конструкциями (±2), у нас еще имеется нечетная модель антиX (±1), поэтому полученные пары также могут быть либо четными, либо нечетными.

(В дальнейшем я буду рассматривать все комбинации на примере моделей роста, то есть со знаком плюс.)

Таким образом, мы можем получить самую простую (единичную) нечетную пару, которая будет иметь вид (+2+1), либо можем получить самую простую (единичную) четную пару, которая будет иметь вид (+2+2).

Здесь необходимо еще добавить (это понадобится нам в дальнейшем).

Нечетная пара (+2+1) имеет приоритет перед четной парой (+2+2). То есть если волновой пакет представлен последовательностью (+2+2+1),

то его мы должны будем представить как (+2(+2+1)). Иначе говоря, вынести нечетную пару (+2+1) отдельно, оставив в начале незакрытую двойку.

При этом необходимо отдельно отметить, что по мере усложнения волновой структуры рынка могут образовываться следующие, гораздо более сложные комбинации пар. Их можно назвать резонансами, так как они представляют собой симметрию.

Эта таблица устроена таким образом, что считает по отдельности общее количество пар. Другими словами, учитывает число нечетных пар (+2+1) и число четных пар (+2+2). Отсюда и получаются первая, вторая, четвертая и восьмая нечетная и четная пары.

Теперь давайте вспомним, что именно в AWA считается волновым циклом.

В альтернативном волновом анализе волновой цикл – это одновременная комбинация четных и нечетных пар одного порядка.

Например, базовый волновой цикл первого ранга (R1) будет соответствовать одновременному формированию второй (21) четной и второй (21) нечетной пары.

При этом цикл второго ранга (R2) будет соответствовать одновременному формированию четвертой (22) четной и четвертой (22) нечетной пары.

Кроме обозначения ранга волнового цикла нам еще понадобится система обозначения таких участков, как полуциклы.

Основное отличие полуциклов от циклов заключается в том, что полуциклы состоят либо только из четных пар, либо только из нечетных пар. Обратите внимание на позиционную структуру полуциклов – она полностью эквивалентна позиционной структуре самих циклов.

Но вернемся к нашим волновым полуциклам.

• Нечетные пары я обозначил буквой M (Men) – мужчины.

• Четные пары я обозначил буквой W (Women) – женщины.

Вот так выглядит сводная таблица полуциклов.

Именно их мы фиксируем в волновом балансе. Ведь именно эти комбинации, являясь симметричными, представляют собой своеобразные резонансы-всплески, создающие барьеры на пути ценового потока. В AWA полуциклы характеризуют форму рельефа русла.

Дробными циклами и полуциклами считаются те же самые комбинации, которые мы рассмотрели выше, но которые состоят при этом не из нецелого, а из дробного числа волновых пакетов.

Выделение циклов

В своей прошлой книге я выделял циклы при помощи дерева, которое я рисовал в волновом балансе.

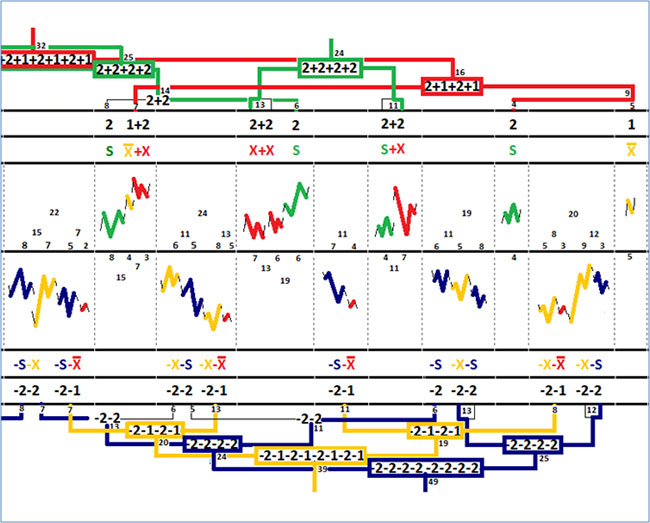
Сейчас я значительно упросил метод отображения и подсчета циклов – я просто выделяю соответствующие участки разными по цвету прямоугольниками. При этом я также указываю параметр интерференции и среднюю длительность цикла.

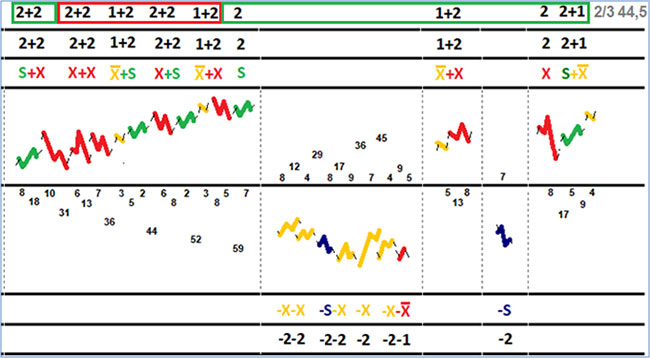
Однако давайте все по порядку.

Чтобы облегчить восприятие материала, я решил воспользоваться нестандартным подходом и в качестве наглядного пособия использовать плиточный шоколад. Да-да, вы не ослышались, именно плиточный шоколад, чтобы на его примере просто и наглядно постараться объяснить, что такое волновые циклы и как они образуются.

При этом рассказывать я буду не просто о плиточном шоколаде, а о том, как его можно делить. Ну что ж, поехали.

Но для начала напомню, что в AWA в качестве своеобразной базы использован простейший волновой цикл (R1).

По модулю он имеет структуру [(+2+1)(+2+2)(+2+2)(+2+1)]. Почему именно такая структура и как она появилась, вы можете прочитать в предыдущей моей книге.

Стоит также отметить, что здесь использована симметричная (относительно центра) структура построения цикла, хотя эта последовательность может быть абсолютно любой.

Главное условие – это определенное количество пар. В данном случае простейший цикл (R1) будет содержать 21 четных пар и столько же нечетных пар. Иначе говоря, две четные и две нечетные пары, а последовательность их расположения никакой роли не играет, так как это суперпозиция.

Но вернемся к шоколаду. Если говорить образно, то простейший цикл (R1) можно представить как своеобразную стандартную плитку шоколада, которую выпускает фабрика под названием «финансовый рынок».

На рисунке ниже вы как раз можете видеть вот такую вот стандартизированную шоколадную плитку, с идеальной центральной симметрией, которая состоит из одного элемента. Такая комбинация представляет собой 1 цикл, состоящий из 1 части (1/1), или просто камень.

Также обратите внимание, что эта стандартная шоколадная плитка разграничена на кусочки (плитки) меньшего размера. Разделена она так неслучайно: только на эти кусочки вы можете разделить шоколад, чтобы поделиться им со своими друзьями.

Смотрите, если разломить эту плитку ровно пополам, то получится два кусочка [(+2+1)(+2+2)] и [(+2+2)(+2+1)]. Такая комбинация представляет собой 1 цикл, состоящий из 2 частей (1/2).

Но эту плитку можно разделить и на две неравные части, например так: [(+2+1)(+2)] и [(+2)(+2+2)(+2+1)].

A можно и так: [(+2+1)] и [(+2+2)(+2+2)(+2+1)]. Но все равно эти комбинации будут представлять собой 1 цикл, состоящий из 2 частей (1/2).

А можно разделить нашу плитку и на три части, например так: [(2+1)(+2)] и [(+2+2)] и [(+2)(2+1)]. Тогда такая комбинация будет представлять собой уже 1 цикл, состоящий из 3 частей (1/3).

Или так: [(+2+1)] и [(+2+2)(+2+2)] и [(+2+1)].

В общем, как вы поняли, вариантов деления может быть много. Но обратите внимание, что нашу плитку можно разделить максимум только на 6 частей. Тогда такая комбинация будет представлять собой уже 1 цикл, состоящий из 6 частей (1/6).

При этом, чем на большее количество частей мы делим нашу плитку, тем меньшими по размеру становятся наши кусочки.

Другими словами, самой маленькой частью может быть [(+2)], чуть больше [(+2+1)], затем [(+1+2+1)], после [(+2+2)] и т. д.

Но в любом случае нашу шоколадную плитку можно разделить максимально только на 6 частей. Однако сей факт совершенно не означает, что вы можете пригласить только 6 друзей, с которыми можно поделиться этим замечательным шоколадом!

Дело в том, что шоколадная фабрика под названием «финансовый рынок» может выпускать шоколад и с большим, чем одна, количеством плиток внутри одной упаковки. Именно из-за этого на рынке могут формироваться достаточно сложные волновые образования, состоящие из нескольких циклов одновременно. Например, 2 цикла из 3 частей (2 цикла из последних 3 волновых пакетов) и т. д.

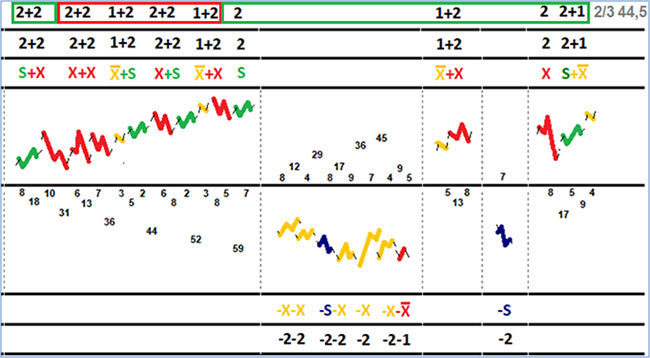
Однако это не самое главное. Основная проблема заключается в том, как именно объединять циклы. Но об этом далее.

О принципе суперпозиции

Принцип суперпозиции является основополагающим методом расчета циклов в альтернативном волновом анализе. Однако прежде, чем мы познакомимся с этим принципом, небольшое предисловие.

Дело в том, что только принцип суперпозиции позволяет вести учет циклов без ухода в бесконечность. Во всех остальных вариантах расчета возникает проблема бесконечности. Постараюсь объяснить, о чем идет речь.

С самого начала я считал циклы, складывая волновые пакеты последовательно, а именно слева направо.

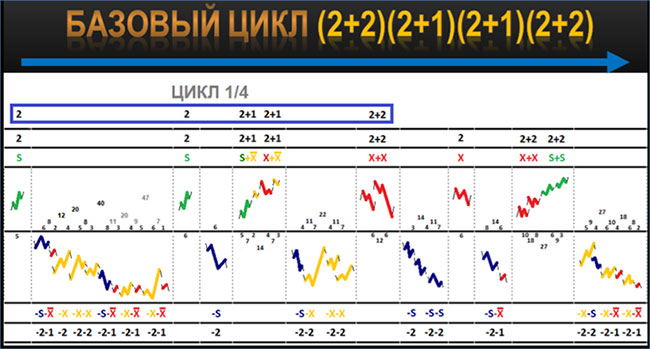
В общем, так, как это показано на изображении: по мере образования циклов слева направо, то есть из прошлого в будущее. Однако при таком подходе начинают оставаться незакрытые волновые пакеты, которые в конечном итоге приводят к проблеме бесконечности.

Суть этой проблемы заключается том, что если добавить к текущему волновому балансу дополнительный участок из прошлого, то общая картина волновых циклов меняется, так как некоторые волновые пакеты начинают образовывать новые циклы с предыдущими, вновь добавленными пакетами.

В результате такого добавления новых исторических данных к уже имеющейся статистике картина волновых циклов постоянно менялась, что приводило к полной неоднозначности процесса их вычислений.

В результате возникала проблема бесконечности, связанная с начальной точкой отсчета. Чисто теоретически получалось, что можно было до бесконечности добавлять все новые и новые участки исторических данных, и это постоянно приводило бы к изменению картины волновых циклов.

В общем, возникала полная неоднозначность, связанная с выбором точки отсчета, или нулевой точки.

Но была одна подсказка. Дело в том, что такая проблема отсутствовала в волновой разметке. Я имею в виду тот факт, что волновая разметка AWA давала абсолютно идентичную картину, как при традиционной разметке (то есть слева направо, иначе говоря, из прошлого в будущее), так и справа налево, то есть от текущего момента и далее в прошлое.

Эта инвариантность не давала мне покоя. Я точно знал, что, если свойства инвариантности проявляются на ценовом графике, значит, точно так же они должны проявляться и волновом балансе при выделении циклов. Дополнительное подтверждение этой идеи я получил, когда подробно ознакомился с принципом формирования стоячих волн в физике.

В общем-то, я и раньше предполагал, что аналогом циклов на финансовых рынках являются стоячие волны в физическом мире, но изучив и осмыслив теорию по ним, я сделал совершенно удивительное заключение: так как стоячие волны с точки зрения физики представляют собой суперпозицию двух противоположно направленных гармонических волн, бегущей и отраженной, то и в случае с финансовыми рынками также необходимо учитывать сразу два направления одновременно.

Бегущая (испущенная) волна – это движение из прошлого в будущее. Отраженная волна – это движение из будущего в прошлое. Другими словами, будущее есть отраженная волна прошлого. Поэтому в качестве эксперимента я решил попробовать провести выделение циклов справа налево, то есть из будущего (от текущей точки) и назад в прошлое.

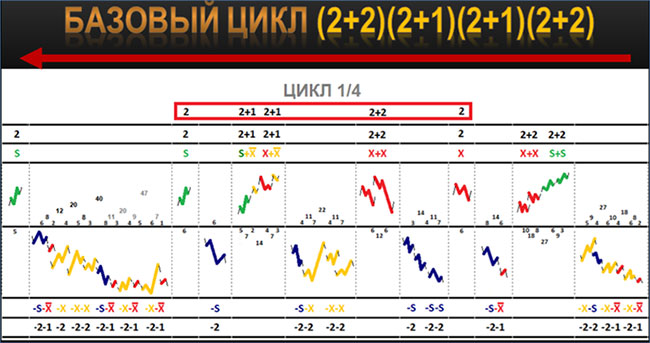
Картина циклов при таком выделении, естественно, отличалась от той, которая получалась в случае традиционного движения из прошлого в будущее (слева направо).

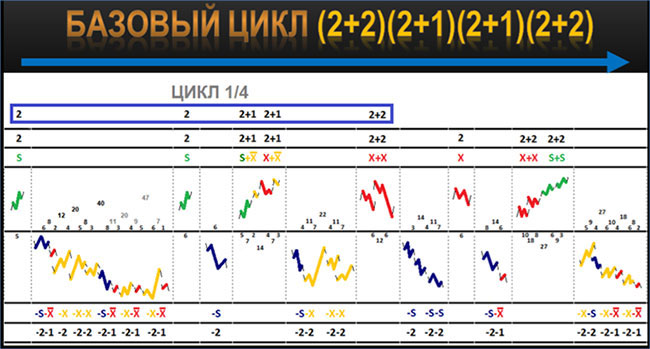
Но затем, разобрав принцип квантовой суперпозиции, я понял, что циклы необходимо формировать именно по этому принципу – другими словами, циклы существуют всегда во всех состояниях одновременно, то есть в суперпозиции, что слева направо, что справа налево по оси времени.

Другими словами, нужно по очереди анализировать – сначала последний волновой пакет, смотреть, не состоит ли он из любого целого числа циклов R1. Потом аналогичным образом анализируются два последних волновых пакета, потом три, четыре и т. д. И все время смотреть, не состоит ли текущая последовательность из любого целого числа циклов R1.

В основном я просчитываю от 1 до 16 последних волновых пакетов (как показывает опыт, этого достаточно). И если в любом из этих вариантов возникает цикл, значит, система фиксирует волновое препятствие, ведь суперпозиция представляет собой геометрическую сумму всех возможных состояний системы.

А теперь предлагаю подробнее познакомиться с понятием суперпозиции, которое используется в квантовой механике.

В классической физике объекты можно описывать, придавая им различные параметры, такие как:

• положение;

• скорость;

• масса.

Путем проведения измерений для каждого из объектов в любой момент времени можно точно вычислить значения этих параметров. Однако на уровне микромира все обстоит совсем по-другому.

Дело в том, что в микромире частицы нельзя описать законами классической физики. Связано это с тем, что на квантовом уровне частица может находиться в позиции А:

Или же в позиции В:

Либо в так называемой суперпозиции, которая представляет собой нечто среднее:

В такой суперпозиции положение частицы в позиции А и в позиции В может иметь одинаковую вероятность:

Но бывает суперпозиция, в которой вероятность того, что частица займет положение А, больше, чем вероятность того, что частица займет положение В:

Либо, наоборот, вероятность того, что частица займет положение В, больше, чем вероятность того, что частица займет положение А:

При этом в состоянии суперпозиции частица не находится ни в точке А, ни в точке В:

Она также не находится в двух точках одновременно:

Частица в этом состоянии как бы вообще не имеет позиции:

Она, получается, в своем роде размазана и образует некое облако состояний:

Но все меняется, как только появляется наблюдатель.

Частица начинает менять состояние.

Она может занимать позицию А или позицию В в совершенно случайном порядке:

Таким образом, проводимые наблюдения фиксируют, что частица находится либо в позиции А:

Или что частица находится в позиции В:

Но до того, как появится наблюдатель, невозможно определить, какую позицию займет частица:

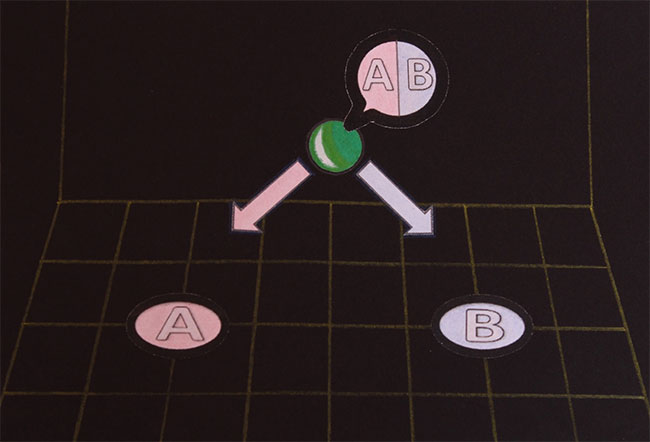
Наблюдение за частицей позволяет ей занять одну из доступных позиций. Хотя и невозможно заранее точно сказать, какую из двух позиций займет частица, тем не менее можно предсказать вероятность ее положения!