
Полная версия
Моделирование синергетических систем. Метод пропорций и другие математические методы. Монография

В. И. Шаповалов
Моделирование синергетических систем
Метод пропорций и другие математические методы
Монография

Предисловие
C середины 70-х годов прошлого века успешно развивается сравнительно молодая наука синергетика. Используя методы нелинейной динамики, она наряду с теорией неравновесных процессов изучает явление самоорганизации в открытых системах. Одним из главных результатов синергетики стало убедительная демонстрация универсальности математических моделей в самых разнообразных по своей природе системах: от физических до экономических и социальных. За последние годы эта наука доказала свою эффективность практически во всех сферах человеческой деятельности, связанных в той или иной степени с процессами самоорганизации. Недаром изучение синергетических принципов вошло в учебный план дисциплины «Концепции современного естествознания», преподаваемой на первых курсах высших учебных заведений.
Однако преимуществами этой науки на сегодняшний день мало кто смог воспользоваться на практике. Причиной этого является с одной стороны большая загруженность синергетики математическим аппаратом, а с другой стороны – неумение применять математические знания, полученные в вузе.
В то же время очевидно, что в современном усложняющемся обществе в любой сфере деятельности долгосрочное планирование невозможно без знаний количественных соотношений важнейших параметров. Разумеется, интуитивное предвидение по-прежнему играет не последнюю роль. Однако ставка только на него приводит к потере эффективности принятых мер. Несмотря на то что математические методы в биологии, социологии и экономике применялись учеными весьма давно (например, в начале прошлого столетия наблюдался бурный рост публикаций подобного рода), до сих пор многие специалисты, занимающиеся практической деятельностью, затрудняются, как уже было сказано, применять математические знания, полученные во время учебы в вузе.
Кроме того, тематически весьма насыщенные учебные программы при ограниченном числе учебных часов часто не позволяют останавливаться более подробно на практическом приложении теории. В результате у значительной части студентов – среди будущих экономистов и социологов – создается неверное представление об отрыве математической дисциплины, читаемой им несколько семестров, от реальной жизни. В жесткой же конкурентной борьбе неумение построить математическую модель (хотя бы простую) применительно к возникшей ситуации чревато заведомым проигрышем. Экономика с преобладанием таких специалистов вынуждена замыкаться на себя, поскольку за ее пределами является неконкурентоспособной.
В монографии подробно на конкретных примерах рассматривается методика построения математических моделей, позволяющих а) формулировать количественные соотношения важнейших параметров; б) прогнозировать тенденции; в) получить необходимое начальное представление о синергетическом моделировании процессов в природе и обществе.
Эта методика включает в себя как обязательный элемент составление так называемых главных пропорций. Под главной пропорцией понимается соотношение между изучаемыми величинами, взятое из опыта (сформулированное на основе практических наблюдений). Эффективность метода главных пропорций для создания математических моделей очень хорошо продемонстрирована в знаменитом труде В. Вольтерра «Математическая теория борьбы за существование», изданном во Франции еще в 1931 году [3]. Значительно позднее немецкий ученый Г. Хакен, основатель синергетики, показал эффективность этого метода при моделировании процессов самоорганизации в системах различной природы [18–20]. Одним из главных преимуществ метода главных пропорций является его сравнительная простота. Мы рассмотрим его приложение а) для составления обыкновенных дифференциальных уравнений, с помощью которых математическим языком можно описывать эволюцию интересующей нас системы; б) для составления точечных отображений (отображений Пуанкаре) с целью анализа устойчивости изучаемой системы, подчиняющейся марковским процессам (в частности, таким процессам подчиняется система «рынок товаров и услуг»). В монографии приведены детальный анализ и подробное решение целого ряда задач, которые могут быть использованы на практических занятиях учебных курсов «Математический анализ» и «Теория вероятностей и математическая статистика», читаемых в вузах как для гуманитарных, так и для технических специальностей.
Введение
Одним из основоположников современных представлений о самоорганизации является профессор Штуттгартского университета Г. Хакен. Еще в начале 1970-х годов Хакеном было замечено, какую важную роль в самоорганизующихся системах играют самосогласованные, коллективные движения частиц. Тогда же им был введен в современный научный язык термин «синергетика», которым теперь обозначается область науки, включающая в себя изучение любых кооперативных явлений природы.
По гречески слово synergeia означает коллективное (совместное) действие. Поэтому в своем названии синергетика как бы подчеркивает тот факт, что при объединении частиц в систему возникает новое качество, присущее только «коллективу» частиц. Заметим, что возникновение у системы нового качества означает, что появилась новая структура, порождающая это качество, т. е. произошла самоорганизация1. Поэтому синергетику часто называют наукой о самоорганизации.
Синергетические системы – это открытые (незамкнутые) системы2. В подавляющем числе случаев именно с такими системами нам приходится иметь дело. Характерной чертой современных исследований в области синергетики является упор на изучение нелинейного поведения. Под нелинейным поведением понимается неоднозначная реакция системы на внешнее воздействие. С математической точки зрения нелинейность возникает тогда, когда уравнение имеет несколько решений. Например, квадратное уравнение имеет два решения, кубическое – три, и т. д. В окружающем нас мире нелинейность проявляется в виде многовариантного поведения, т. е. когда у системы появляется возможность выбора из нескольких новых состояний.
Под внешним воздействием система становится открытой. В нелинейной динамике изменение внешнего воздействия соответствует изменению управляющих параметров. Управляющими параметрами называются константы (постоянные величины), входящие в эволюционное уравнение [2,14, 20]. В качестве последнего выступает уравнение вида
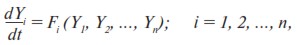
где Yi – переменные системы; t – время; Fi – функция переменных, вид которой определяется свойствами системы; n — количество переменных, минимально необходимое для описания исследуемого процесса.
Управляющие параметры представляют в эволюционном уравнении (1) внешние условия, которые система изменить не может, и поэтому вынуждена под них подстраиваться [20]. Например, если система движется по выпуклой или вогнутой поверхности и при этом на нее действует сила тяжести и сила сопротивления среды, то в правую часть уравнения (1) в качестве постоянных величин войдут кривизна поверхности, ускорение свободного падения и коэффициент сопротивления среды. Эти постоянные величины будут управляющими параметрами. Изменить их система не может, поэтому ей придется двигаться, подстраиваясь к ним. В частности, она будет двигаться в направлении от выпуклости к вогнутости. Если мы изменим кривизну поверхности, поменяв, например, выпуклое на вогнутое, то это сразу же скажется на движении системы – оно изменится на обратное. Другими словами, изменяя значения указанных параметров, внешний мир управляет поведением системы. Собственно, поэтому эти параметры и названы управляющими.
Эволюционными уравнениями вида (1) описываются объекты весьма широкого класса. В том числе и такие, какие не могут быть отнесены к системам, например материальная точка. Предметом же настоящей книги являются самоорганизующиеся системы. В связи с этим необходимо уточнить, что мы понимаем в (1) под переменными Yi.
Прежде всего, предполагается, что нам известно, какие части системы являются ее элементами. Отдельные группы элементов могут образовывать подсистемы данной системы (в предельном случае подсистема может быть одна, т. е. совпадать с самой системой). Так вот, переменные Yi в эволюционном уравнении – это переменные, описывающие связи между подсистемами. Иными словами, отдельная Yi символизирует некоторую обобщенную характеристику коллективного движения элементов подсистемы.
Только при таком понимании Yi эволюционное уравнение (1) может описывать самоорганизацию. Действительно, если внешний мир изменит управляющие параметры, то процесс подстраивания системы к новым их значениям проявится в том, что элементы подсистем, представленных в (1) в виде обобщенных переменных, изменят свое коллективное движение. Это следует из того, что в (1) изменение управляющих параметров непосредственно влияет на значения Yi, т. е. на подсистемы, а не на их элементы. Следовательно, элементам придется самопроизвольно изменить взаимодействие между собой, чтобы их коллективное движение стало соответствовать новым значениям управляющих параметров. Иначе говоря, в системе произойдет самоорганизация (см. определение самоорганизации в первой сноске на с. 5).
Итак, в данной книге под переменными Yi в (1) мы понимаем макроскопические переменные, соответствующие некоторым обобщенным характеристикам коллективного движения элементов системы. Напомним, что в синергетике такие переменные называются параметрами порядка [19].
Математически создание синергетической модели, как правило, начинается с выбора параметров порядка, т. е. с выбора макроскопических переменных, количественно характеризующих основные связи в системе. Следующий шаг заключается в составлении пропорций, формирующих эти связи. Правило составления пропорций подробно описано в [19] (см. также [3]). Согласно этому правилу, увеличение некоторой величины с течением времени пропорционально приросту этой величины минус ее потери. Затем эти пропорции преобразуются в эволюционное уравнение типа (1).
Глава 1
Применение некоторых известных дифференциальных уравнений для создания моделей социальных и экономических систем
1.1. Экстремальное поведение большой группы людей
Если какой-либо объект представляет собой систему, то он обязательно подчиняется универсальным системным закономерностям. Социальные системы не являются исключением. В частности, коллективное поведение людей в простейшей экстремальной ситуации наглядно демонстрирует качества, которые могут наблюдаться в поведении, например, физических систем.
Допустим, что в здании находится большая группа людей. В некоторый момент времени, принятый за начальный, все люди пытаются выйти из здания. Мы хотим получить закон, показывающий, как с течением времени уменьшается число людей в здании [28].
Введем обозначения: N – количество людей, находящихся в здании в произвольный момент времени t; dN – количество людей, вышедших из здания за время dt. Сформулируем начальное условие: в момент времени t = 0 количество людей в здании равнялось N0.
Составляем главную пропорцию задачи (см. введение, последний абзац). Делается это следующим образом. Из общих соображений можно предположить, что число людей, вышедших из здания за некоторый промежуток времени, пропорционально самому промежутку времени и количеству людей, находящихся в здании:
dN ~ dt, N.
Заменяя знак пропорции на коэффициент пропорциональности А, получим
dN = —ANdt,
или

Эволюционное уравнение данной задачи (сравните с (1)). Появление минуса объясняется тем, что с увеличением t уменьшается N (dN < 0).
Данное уравнение представляет собой известное дифференциальное уравнение с разделяющимися переменными. Поступаем согласно методу решения, описанному в разделе П1.2 Приложения. Сначала разделяем переменные по разные стороны уравнения, затем полученное выражение интегрируем:
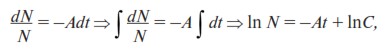
где C – постоянная интегрирования. Выразим N:
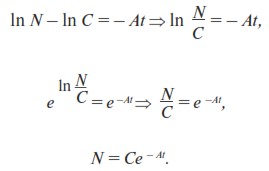
Постоянную C определим из начального условия. В нашей модели начальное условие будет выглядеть следующим образом (см. в Приложении формулу (П.1)):
N│t = 0 = N0.
В соответствии с этим условием мы в (2) подставим t = 0 и N0 вместо N:
N0 = Ce – A ∙ 0 = Ce0 = C.
Следовательно, C = N0. Тогда (2) примет окончательный вид
N = N0 e—At.
Итак, мы получили закон, показывающий, как с течением времени уменьшается количество людей в здании. Здесь постоянная А характеризует архитектурные особенности здания: количество этажей, количество выходов и т. п.
Как видим, поведение людей, покидающих в экстремальной ситуации здание, будет таким, чтобы совместными действиями реализовать закон экспоненциального уменьшения числа людей в здании.
Нетрудно заметить, что данный закон по своему математическому виду совпадает с известным в физике законом радиоактивного распада:
N = N0 e—At; N – число нераспавшихся атомов,
что наглядно демонстрирует универсальность системного подхода к явлениям в природе и обществе.
1.2. Модель воздействия рекламы на количество покупаемого товара
(Изложение данного раздела следует работам [23, 28].) Как и в предыдущем разделе, мы воспользуемся методом составления главных пропорций.
Пусть за время dt приобретается dy товара (y – количество некоторого товара). Наблюдение за применением рекламы показывает, что в результате действия рекламы происходит ускорение приобретения товара с течением времени. Математически ускорение представляет собой вторую производную по времени, поэтому предыдущее утверждение можно записать в виде следующей пропорции:
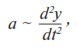
или
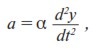
где a – потенциальное действие рекламы; α – коэффициент пропорциональности.
Уравнение (3) характеризует потенциальное действие рекламы. Однако на практике ее действие испытывает влияние различных факторов, как способствующих, так и мешающих восприятию рекламного материала. Все эти факторы разделяются на две основные группы: F1 – факторы, связанные с особенностями товара; и F2 – факторы, связанные с особенностями покупателя. Математически влияние этих групп можно учесть, добавив их в левую часть уравнения (3) (в левую, так как они влияют именно на действие рекламы a):
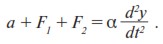
Перечень конкретных факторов, в той или иной степени имеющих отношение к группам F1 и F2, может быть очень велик. Из этого перечня, следуя идее метода основных пропорций, мы выберем главные факторы, обязательно присутствующие в любой операции купли-продажи.
В группе F1 среди качеств товара, влияющих на восприятие рекламы, определяющим является уровень его доступности для покупателя. Действительно, какими бы достоинствами ни обладал товар и как бы необходим он ни был, его широкая доступность снижает актуальность любой информации о нем. Поэтому для группы F1 в качестве определяющего фактора мы выбираем насыщенность рынка данным товаром. Соответствующая пропорция имеет вид:
F1 ~ y, откуда: F1 = – γy.
Здесь: γ – коэффициент пропорциональности, а минус указывает на то, что с увеличением количества товара на рынке снижается восприятие его рекламы (т. е. на то, что этот фактор должен уменьшать а в левой части уравнения (4)).
В группе F2 определяющим фактором является доход среднего покупателя. Это следует из того, что, каким бы желаемым ни был товар, если доход не позволяет его приобрести хотя бы в ближайшем будущем, то реакция на его рекламу будет снижена. На практике доход находит свое выражение через объем спроса. Последний же, как известно, представляет собой количество товара, который мог бы приобрести покупатель за определенный промежуток времени, что в математике соответствует первой производной по времени: dy/dt. Поэтому для этой группы факторов основная пропорция будет иметь вид:

Здесь: β – коэффициент пропорциональности; минус указывает на разные знаки у dt (t ↑, dt > 0) и dy (y ↓, dy < 0). Последнее следует из того, что в странах, в которых имеется инфляция, доход среднего покупателя с течением времени падает.
С учетом сказанного уравнение (4) запишется следующим образом:
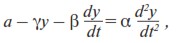
откуда

Это известное линейное неоднородное дифференциальное уравнение с постоянными коэффициентами (НОЛУ). Уравнение (5) решаем стандартными математическими методами (метод решения НОЛУ см. в Приложении, раздел П1.4):
y = y* + y1, (6)
где y* – общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (ОЛУ); y1 – частное решение НОЛУ.
Общее решение y* найдем из уравнения, в которое превращается (5) при замене правой части на 0. В этом случае НОЛУ переходит в ОЛУ (см. Приложение, раздел П1.3):

Воспользовавшись методикой решения ОЛУ, описанной в разделе П1.3 Приложения, составим и решим характеристическое уравнение:

Чтобы определить принадлежность корней k 1,2 к действительным или комплексным числам, необходимо знать знак разности β2 – 4αγ. Для этого раскроем смысл постоянных коэффициентов α, γ и β.
Постоянная α появляется как коэффициент пропорциональности в уравнении (3), отвечающим за потенциальное действие рекламы. Отсюда смыл этого коэффициента заключается в том, что он обобщает собой условия, благоприятные для создания рекламы. Благоприятные потому, что, как видно из (3), чем больше значение α, тем больше a – потенциальное действие рекламы. В частности, α будет иметь малое значение в том обществе, в котором не используются современные рекламные технологии, и большое значение в противоположном случае.
Постоянная γ появляется как коэффициент пропорциональности в группе факторов F1. Чем больше значение γ, тем больше влияние F1 на а, и наоборот. Поэтому γ должна характеризовать степень доступности товара в данном регионе.
Постоянная β является коэффициентом пропорциональности в группе факторов F2. От ее значения зависит, как изменение дохода (dy/dt) среднего покупателя сказывается на восприятии им (покупателем) рекламы. Если β мало, то это означает, что изменение дохода мало влияет на величину F2. В частности, в странах с высоким уровнем жизни большинства граждан значение β должно быть достаточно малым.
Таким образом, в экономически развитых регионах α и γ должны иметь сравнительно большие значения, а β – малое. Поэтому β2 – 4αγ < 0, т. е. в выражении для k1,2 разность под корнем имеет отрицательный знак. Следовательно, k1,2 – комплексные:
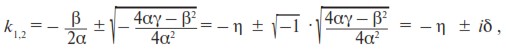
где
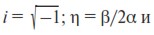

Как видим, k1,2 соответствуют 4-му типу решения ОЛУ (см. Приложение, раздел П1.3). В этом случае решением уравнения (7) является выражение
y* = е– ηt (A1 cos δt + A2 sin δt), (9)
где A1 и A2 − константы интегрирования.
Частное решение y1 определим по виду правой части уравнения, в качестве которой в (5) выступает a/α. Последнее соответствует первому виду правой части НОЛУ (см. Приложение, раздел П1.4), а именно
f (t) = p (t) e γt. (10)
Действительно, для уравнения (5) функцию f (t) можно записать как
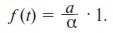
Сравнивая между собой (10) и (11), находим, что в нашей задаче
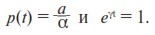
Напомним, что число, возведенное в степень, равно единице только в том случае, если степень равна нулю. Следовательно, γ = 0. Как видим, γ не совпадает с корнями характеристического уравнения k1,2. Поэтому для y1 выбираем первый тип решения (выбираем пункт 1.а из раздела П1.4 Приложения):
y1 = q(t) eγt = q(t)
(eγt = 1, см. (12)). Определим вид q (t). Для этого учтем, что: а) q (t) – многочлен той же степени, что и р (t); б) в нашем случае р (t) – многочлен нулевой степени:

Следовательно, и q(t) является многочленом нулевой степени, т. е. является постоянной величиной. Обозначим эту постоянную, например, с: q(t) = c. Тогда
y1 = q(t) = c. (13)
Постоянную с найдем, подставив y1 в (5):

Воспользуемся (13):
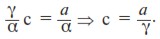
Здесь мы учли, что
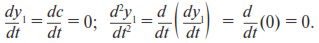
Найденное значение с подставим в (13):
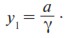
– частное решение уравнения (5). Его общее решение запишем по формуле (6) (y* возьмем из (9)):
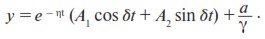
Выражение в скобках можно упростить, заменив постоянные A1 и A2 на новые постоянные A и φ0 по формулам
A1 = A sin φ0 и A2 = A cos φ0
(легко увидеть, что

A1 cos δt + A2 sin δt = A (sin φ0 cos δt + cos φ0 sin δt) = A sin (δt + φ0).
В результате (14) примет вид

Уравнение (15) представляет собой формулу зависимости от времени количества товара, приобретаемого благодаря действию рекламы.
Из (15) следует, что если рекламировать товар с постоянной интенсивностью достаточно долго (a = const), то начнутся колебания y вокруг постоянного значения a/γ, т. е. возникнет чередование периодов положительного и отрицательного восприятия рекламы (см. рис. 1).
Сравним (15) с известным законом колебательного движения
x = A sin (ωt + φ0).
Как видим, δ совпадает по смыслу с циклической частотой ω. Отсюда, воспользовавшись соотношением для периода колебаний T = 2π/ω, получаем формулу для промежутка времени положительного восприятия рекламы:
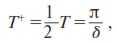
где δ вычисляется из (8). Для определения численных значений коэффициентов, входящих в (8), возможно использование эконометрических методов.

Рис. 1. Чередование периодов положительного и отрицательного восприятия рекламы

