Логика. Краткий конспект

Таким образом, современная логика была создана математиками для решения проблем, возникших в основаниях математики. Тем не менее достаточно скоро обнаружилось, что, во-первых, созданный математиками логический аппарат может найти применение не только в математике: многие философы попытались, и довольно успешно, по-новому взглянуть с его помощью на традиционные философские проблемы; затем он нашел довольно эффективное применение в информационных технологиях и кибернетике, в анализе естественного языка, во многих других сферах. Во-вторых, практически немедленно после его появления он сам стал предметом пристального внимания. Критическое обсуждение некоторых фундаментальных принципов новой логики уже в 1920-е гг. привело к тому, что начали формироваться различные направления неклассических логик, многие из которых не были связаны с проблемами обоснования математики. Поэтому не совсем правильно характеризовать современную логику как математическую логику, если под этим понимается не более чем один из разделов математики. Ее можно считать математической в смысле знаменитого афоризма, авторство которого приписывается П. С. Порецкому (1846–1907), автору первого в России лекционного курса по математической логике, согласно которому математическая логика, будучи «современной теорией правильного рассуждения», есть «логика по предмету и математика по методу».

1.3. ОБ ОСОБЕННОСТЯХ ФОРМАЛИЗОВАННЫХ ЯЗЫКОВ

Современные логические теории строятся на основе некоторого специально создаваемого для этих целей языка. Теория языка, даже если речь идет о формализованном языке логических теорий, строго говоря, не является разделом логики. Тем не менее, учитывая, что формализованный язык является необходимым условием для построения логической теории, мы не можем не уделить ему некоторого внимания.

Искусственные языки, используемые при построении логических теорий, называют формализованными, поскольку их цель состоит в том, чтобы точно отобразить логическую форму выражений, используемых в рассуждении. Это сразу позволяет нам указать первое отличие этих языков от естественных. В первом приближении можно выделить две функции языка: коммуникативную и репрезентативную. Язык может выступать, во-первых, как средство общения и, во-вторых, как средство выражения. Искусственные языки, создаваемые для научных целей, к которым относятся и языки логики, не предназначены для общения: они выполняет только вторую функцию – репрезентативную.

Язык конкретной теории называется объектным языком, или языком-объектом. Для описания такого языка требуется метаязык. По своим выразительным возможностям он должен быть, по крайней мере, не беднее объектного языка. При этом разделение на метаязык и язык-объект не является абсолютным: один и тот же язык может выступать как в роли метаязыка, так и в роли языка-объекта. Так, в русском учебнике немецкого языка русский язык будет являться метаязыком, а немецкий – объектным языком; в случае же немецкого учебника по русскому языку дела будут обстоять наоборот.

Построение языка начинается с задания его алфавита. В отличие от естественного языка алфавит формализованного языка представляет собой список всех базисных (или примитивных) символов, используемых в языке. Этот список варьируется в разных теориях в зависимости от того, какие именно свойства требуется формализовать в рамках той или иной теории. Для этого алфавита затем надо указать правила синтаксиса, семантики и прагматики. Необходимость этих трех теорий для полного описания языка установлена, в частности, в рамках семиотики – общей теории знаковых систем. Эти три стороны характеризуют любую знаковую систему.

Синтаксис исследует связи между знаками некоторого языка, правила их соединения. При этом не принимаются во внимание вопросы о том, что именно стоит за этими знаками, т. е. что они означают. Семантика исследует отношения между знаками и тем, что ими обозначается. Проще говоря, семантика – это описание смысла используемых в языке знаков, а также смысла сложных выражений, которые можно построить по законам синтаксиса. Прагматика занимается ситуативными параметрами, оказывающими влияние на семантические и синтаксические свойства выражений языка. Например, мы не можем установить, истинно ли предложение «Я сегодня счастлив», пока не выясним, кто именно скрывается за местоимением «я» и что именно за день обозначен словом «сегодня». Прагматика занимается формальными свойствами предложений, содержащих такого рода указатели, отсылающие к некоторой ситуации. Сразу отметим, что в нашем учебнике вопросы логической прагматики затрагиваться не будут.

Между естественными и искусственными языками можно заметить то различие, что, когда мы занимаемся, например, синтаксисом некоторого естественного языка, последний выступает перед нами как данность и наша задача – раскрыть присущие этому языку синтаксические закономерности. Искусственные же языки создаются для определенных целей, и в зависимости от этих целей мы сами задаем необходимые для их достижения правила синтаксиса. Поэтому искусственные языки значительно беднее естественных по широте выразительных возможностей, но позволяют достигать такой строгости и точности при описании стоящих перед ними задач, которые естественному языку либо недоступны, либо достигаются ценой невероятного многословия и (или) противоестественного искажения привычных способов выражения. Чтобы осознать, что это действительно так, попробуйте описать словами обычного русского языка какое-нибудь тригонометрическое уравнение третьей степени, не используя специальных математических терминов. Поэтому Лейбниц и Фреге любили уподоблять отношение между естественным и искусственным языком отношению между глазом и микроскопом: глаз несравненно гибче, чем микроскоп, он выполняет намного больше функций. Микроскоп же предназначен для решения едва ли не единственной задачи, но это такая задача, перед которой обычный человеческий глаз просто бессилен.

В примерах, рассмотренных в § 1.1 мы делали подстановки конкретных значений вместо переменных. При этом логическая форма рассуждения, как мы обратили внимание, оставалась неизменной. Это дает нам первую, простейшую и фундаментальную классификацию символов, используемых в формализованном языке.

Во-первых, это логические символы, которые задают логическую форму и должны оставаться постоянными. Во-вторых, нелогические – они должны обозначать элементы содержательного характера, которые допускают замену: президенты, города, числа и т. п. Такие символы обычно выступают в качестве переменных. В-третьих, для построения выражения языка требуются вспомогательные (технические) символы, которые сами по себе ничего не обозначают.

Некоторые основные понятия семантики

Некоторые базисные принципы логической семантики были заложены в работах Г. Фреге. В центре его внимания оказались семантические свойства категории «Имя». По его мнению, имя имеет две характеристики: смысл и значение. Значение – то, на что имя указывает, это предмет, для обозначения которого служит имя. Смысл – это информация, сообщаемая именем. Благодаря тому что имя имеет смысл, мы его понимаем. Принято говорить, что имя выражает смысл и указывает на значение. При этом не всякое имя, обладающее смыслом, имеет и значение. Таковы литературные персонажи, сказочные и мифические герои, а также выражения вида «круглый квадрат» и «самое большое натуральное число». Последние являются осмысленными – ведь именно благодаря этому мы их понимаем; в частности, мы понимаем, что предмета, обозначенного подобным именем, существовать не может. Таким образом, имя указывает на объект при посредстве смысла; при этом, двигаясь из пункта «имя» в пункт «значение», можно застрять в пункте «смысл» и не добраться до цели. Поэтому линия между именем и его значением на рис. 1.1 проведена пунктиром.

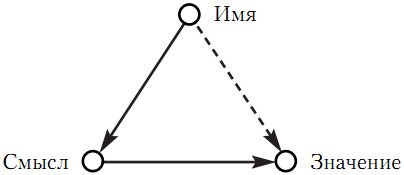
Рис. 1.1

Тот факт, что один и тот же предмет может обозначаться разными именами, возможен благодаря тому, что эти имена имеют одинаковые значения, но разные смыслы. Поэтому, считает Фреге, различение смысла и значения позволяет объяснить, почему мы можем ставить знак равенства в выражении «А = В», хотя А и В суть разные вещи. Мы вправе делать это тогда, когда А и В имеют одинаковые значения, несмотря на то что они имеют разные смыслы. Больше того, на этом основании мы вправе заменять А и В друг на друга, сохраняя при этом уверенность, что значение более сложного выражения, в рамках которого производится такая замена, не изменится.

Эта теория становится особенно продуктивной, если мы вслед за Фреге распространим ее на предложения. Фреге рассматривал последние как частный случай имен. Смыслом предложения он счел выражаемую им мысль, или то, что в логике обычно называется суждением, а вот значением – его истинностное значение, истину или ложь. Эта теория стала очень резонансной и широко обсуждаемой, причем не только в логике. Здесь мы отметим лишь, что она позволяет обосновать принципы дедуктивных переходов между высказываниями, выраженными в некотором языке. Мы можем переходить от высказывания А к высказыванию В на том основании, что они имеют одинаковые значения, будучи при этом различными по смыслу. Таким образом, понятие смысла как бы выносится за скобки, оно не принимается во внимание; логические связи и отношения устанавливаются и изучаются только на основе значения языковых выражений. По крайней мере, в классической логике дела обстоят именно так.

Существуют, тем не менее, контексты, в которых замена одного предложения на другое на том основании, что они имеют одинаковые значения, недопустимо. Например, в предложении «Колумб считал, что земля шарообразна» входящее в него предложение «Земля шарообразна» нельзя заменить на предложение «Петербург – город на Неве», хотя оба они имеют значение «истина». Ведь тогда вместо истинного исходного предложения мы получим ложное. В таких контекстах приходится принимать во внимание смыслы выражений. Подобного рода контексты называются интенсиональными, и их исследования осуществляются в рамках неклассических логик.

Надо сказать, что, когда мы пытаемся прилагать эту теорию к определенным видам имен, в нее приходится вносить изменения. Возьмем, например, собственное имя. Собственным именем называется имя, которое предназначено для указания на один, и только один объект. Многие собственные имена, которые мы встречаем в повседневной жизни, не удовлетворяют этому определению, т. е. они не являются собственными в логическом смысле. Действительно, возьмем ли мы имена или фамилии людей, клички животных, нередко даже названия населенных пунктов – эти имена, как правило, обозначают более чем один объект. Логические же собственные имена – это имена уникальных объектов, это своего рода ярлыки, которые приклеиваются к вещам: одна вещь – один ярлык. Обозначение объекта с помощью собственного имени можно уподобить указанию на него пальцем: в последнем случае мы не сообщаем о предмете никакой информации, мы только указываем на него. Исходя из подобных соображений Б. Рассел утверждал, что собственное имя имеет значение, но не имеет смысла.

Следующий вид имен – общие имена. Общими называются имена, предназначенные для указания на произвольный объект определенной области. Примерами общих имен могут служить такие имена, как «человек», «число», «закон». Для них уже сам Фреге усложнил свою схему. Он полагал, что эти имена указывают на объект не напрямую, но посредством такой сущности, как понятие. Именно понятие, по его мнению, является значением общего имени. Под понятие, в свою очередь, подпадают определенные объекты. При этом число объектов, подпадающих под понятие, может изменяться от нуля до бесконечности. Взаимосвязь общего имени с указанными компонентами иллюстрируется на рис. 1.2.

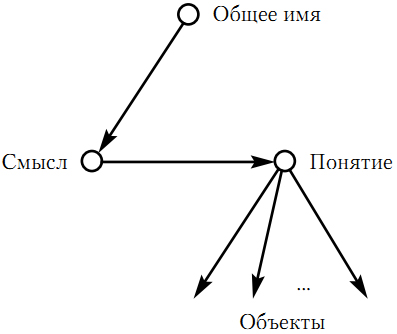
Рис. 1.2

Тем не менее, каковы бы ни были особенности этой теории применительно к различным видам имен, для всех них в классической логике имеют силу следующие принципы употребления имен:

1) всякое имя является именем предмета;

2) любое имя, являющееся частью более сложного имени, может быть заменено другим именем, имеющим такое же значение, и при этом значение сложного имени не изменится.

Первый из них является принципом предметности, второй – принципом взаимозаменимости.

Что понимать под значением имен, содержащих переменные? Предложение «5 >4» имеет значение «истина», предложение «3 >5», имеет значение «ложь», но каково значение «x >у»? Вопрос этот не праздный, поскольку отношение следования устанавливается между формами высказываний, которые, как мы выяснили выше (с. 5), содержат переменные. Но логические отношения между выражениями устанавливаются исходя из значений этих выражений. Для преодоления этой трудности вводится понятие интерпретации. Интерпретация – это некоторое произвольное присваивание значений переменным, входящим в данное выражение. Так, примеры 1.3 и 1.4 являются разными интерпретациями примера 1.2. Пример 1.3 получается в результате присвоения переменным х, у, и z значений 3, 5 и 4 соответственно. Предложение «Санкт-Петербург севернее Москвы» можно понимать как одну из интерпретаций выражения «х севернее у», а именно такую, где переменной х присвоено значение «Санкт-Петребург», а переменной у – значение «Москва». Очевидно, что на одних интерпретациях выражения, содержащие переменные, становятся истинными, а на других – ложными. Интерпретация, на которой выражение принимает значение «истина», называется моделью. С помощью этих понятий мы можем дать более точное определение отношению следования:

Высказывание А является логическим следствием из множества высказываний {X}, сокращенно {X} |= А, если и только если каждая интерпретация, делающая истинной все высказывания, входящие в {X}, делает истинным и высказывание А.

Или короче:

Высказывание А является логическим следствием из множества высказываний {X}, сокращенно {X} |= А, если и только если каждая модель {X} является моделью А.

Тема 2

ЛОГИКА ВЫСКАЗЫВАНИЙ

Первый, наиболее простой раздел современной логики – это логика высказываний. Простейшим элементом в этом разделе выступает высказывание. Сначала установим некоторые терминологические различения.

2.1. ВЫСКАЗЫВАНИЕ, СУЖДЕНИЕ, ПРЕДЛОЖЕНИЕ

Предложение – языковое средство выражения высказывания. Одно и то же высказывание может быть выражено разными предложениями. Например, предложение русского языка «Знание – сила» выражает то же самое высказывание, что и английское предложение «Knowledge is power» или латинское «Scientia potentia est».

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.