Все науки. №3, 2023. Международный научный журнал

Когда путь одного числа настолько сильно отличается даже от соседнего, как вообще подступиться к доказательству подобной гипотезы? Разумеется, все математики были в растерянности и абсолютно никто не мог решить эту задачу. Так Джефри Лагариас – мировой эксперт по этой проблеме, и он говорил, что никому не стоит браться за эту проблему, если он хочет стать математиком. Была проведена масштабная работа и изучено огромное количество чисел-градин, стараясь найти закономерность. Здесь можно утверждать, что все значения приходят к единице, однако, что можно сказать о пути, который совершают все числа? Интересно то, что этот путь абсолютно случаен.

Для примера можно привести график всех значений данного алгоритма от 1 до 100 (Рис. 2).

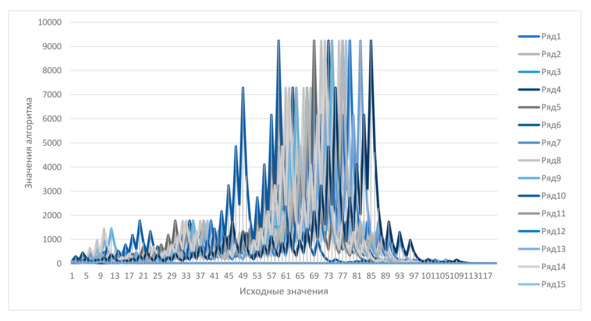
Рис. 2. График значений для чисел-гранул от 1 до 100

Как можно увидеть, чаще всего изначально начинается рост и после резкий спад, при этом значение числа просто не рассмотреть, однако, если сделать график логарифмическим, в его колебаниях прослеживается нисходящий тренд. Его также можно наблюдать на рынке акций в день обвала, что не случайно, ибо это примеры геометрического броуновского движения, то есть, если взять логарифмы и вычислить линейную компоненту, колебания кажутся случайными, как если бы на каждом шаге бросали монетку. И если рассматривать данный анализ функции, как часть математического анализа, то тут начинает прослеживаться явная связь с теорией вероятности. Откуда получается, что когда получается орёл – линия идёт вверх, а когда решка – вниз, откуда и получается особый график.

Если же рассматривать данный график при сопоставлении с той же биржей, то это скорее в краткосрочном анализе, хотя в долгосрочной перспективе, акции всё же растут, а «3x+1» падает. Ещё можно обратить внимание на старший разряд чисел градиент – это означает гистограмму, который получается, подсчитать количество цифр, с которых начинаются числа в ряде гранул для того или иного числа алгоритма. Если каждый раз добавлять эти значения, для 1, 2, 3 и т.д., получается всё больше и больше данных, при этом соотношение высоты столбиков становиться всё более упорядоченным.

Так для первого миллиарда последовательностей самым частым значением оказывается единица, 29,94% всех случаев, 2 – 17,47%, 3 – 12,09%, 4 – 10,63%, 5 – 7,94%, 6 – 6,16%, 7 – 5,76%, 8 – 5,31%, 9 – 4,7% и чем цифра больше, тем реже она оказывается впереди.

Подобный расклад характерен не только для чисел-градин, примером много, это и население стран, и стоимость компаний, все физические константы или числа Фибоначчи, и много чего ещё. Этот закон называется законом Бенфорда. Удивительно, но если проследить в налоговых декларациях нарушение закона Бенфорда, можно даже определить факт мошенничества. Этот закон также помогает определить аномалии при подсчёте голосов на выборах или многом другом.

Самое лучшее действие этого закона происходит тогда, когда числа, вводимые в нём, имеют разброс в несколько порядков, как в данном случае, но закон Бенфорда, к сожалению, не может сказать, все ли числа попадают в конце в цикл 4-2-1. Для этого нужно использовать другой метод. Изначально странно, что этот алгоритм приводит все числа к 1, учитывая, что чётных и не чётных чисел поровну и не чётные возрастают более чем в 3 раза, а чётные уменьшаются в 2 раза.

Тут напрашивается вывод о том, что все последовательности по идее должны идти вверх, а не вниз. Но стоит обратить внимание и на то, что всегда, когда производиться операция с не чётным числом, то есть, когда его умножают на 3 и прибавляют 1, оно обязательно превращается в чётное, следовательно, следующим шагом он всегда будет делиться на 2. Получается, что не чётные числа не утраиваются, а умножаются на (3x+1) /2 или точнее на 1,5, ибо 0,5 для больших чисел можно игнорировать. Значит максимальный рост из этого составляет именно 1,5.

Ранее уже был приведён график для всех чисел от 1 до 100, но стоит рассмотреть небольшой случай для всех не чётных чисел. Как известно, во втором шаге они превращаются в чётные значения, а затем ровно половина из них сразу приведён, после деления опять же к не чётному. Но каждое 4 число, придётся делить на 2 дважды, значит, уже эти не чётные числа это ¾ от предыдущего. Каждое 8-е число придётся делить на 2 трижды, чтобы получить не чётное. Каждое 16 четырежды и т. д.

Так взяв, среднее геометрическое, можно увидеть, что для того, чтобы добрать от одного не чётного числа до другого через все чётные числа, нужно умножить его на ¾, что меньше единицы, отсюда и получается, что статистически, эта последовательность уменьшается чаще, чем растёт.

Приведём пример для большого числа, к примеру 341. Его ряд выглядит следующим образом:

341 – 1024 – 512 – 256 – 128 – 64 – 32 – 16 – 8 – 4 – 2 – 1.

У него было только одно не чётное и все чётные числа, чем этот ряд и примечателен. Однако, можно их изображать, как в виде графиков, так и в виде деревьев, показывая, как одно из чисел связано с последующим в своей последовательности, создавая граф.

И если гипотеза верна, значит любое число должно оказаться в этом огромном графе, состоящее в бесконечном количестве «ручейков» образуя в одном потоке цикла 4-2-1. Существует интересная визуализация такого графа, в котором используется алгоритм того, что на не чётных числах, он поворачивается на выбранный угол по часовой стрелки, а на чётных – против часовой стрелки.

В итоге получается интересная изогнутая, чаще в одну сторону структура. Напоминающая коралл, водоросли или дерево на ветру. Но это лишь на малое количество чисел, для огромных массивов, меняя углы поворота можно создавать огромные и ослепительно красивые фигуры, словно порождённые природой.

Гипотеза кажется не верной только в 2 случаях:

1. Если будет найдено число, которое в алгоритме даст бесконечность, то есть на него по неизвестной причине эта «сила притяжения» к 4-2-1 не должно будет действовать;

2. Где-то есть последовательность, которое бы образовало собственный замкнутый цикл, и все числа в нём должны оказаться вне основного графа.

Однако, ни один из этих вариантов пока не найден, хотя уже простым перебором проверены все числа до 2 в 68 степени, что равняется 295 147 905 179 352 825 856 чисел. Точно известно, что все числа из этих значений приходят к циклу 4-2-1. Более того, на основе этих данных рассчитано, что даже если и существует такой особый цикл данных, он должен состоять как минимум из 186 миллиардов чисел. И получается, что все работы указывают на то, что гипотеза верна, но всё ещё не доказывает.

Избирался и другой путь. Был построен график рассеивания, взяв на одной оси сами числа, а на другой значения. Если можно доказать, что в любой последовательности алгоритма есть число меньшее исходного, можно подтвердить гипотезу Коллатца. Но любое исходное числа приведён к числу поменьше, которое по своей же последовательности приведёт к числу ещё меньше и т.д., вплоть до 1.

То есть единственный возможных исход для этого частного случая – это цикл 4-2-1, но доказать это до сих пор не удалось.

Хотя в 1976 году Рихо Террас показал, что почти все последовательности включают в себя значения ниже исходного. В 1979 году показали, что значения будут меньше исходных на эти значения, возведённые в степень 0,869. Позднее, в 1994 году, степень стала точнее – 0,7925. Здесь почти все числа означают, что при стремлении исходных значений к бесконечности, доля ограничивающей функции стремиться к 1. В 2019 же году, математик Терри Тао смог доказать, что этот алгоритм подчиняется ещё более строгим ограничениям.

Ему удалось показать, что все числа будут меньше, чем значения функции в любой точке, при условии, что предел функции, при стремлении переменной к бесконечности будет равна бесконечности. При этом функция может расти сколь угодно медленно, тот же логарифм, или логарифм логарифма, или логарифм логарифма-логарифма и т. д. Это позволяет утверждать, что сколь угодно малые числа есть в ряде любого исходного числа. И как было сказано в 2020 году, лучше этого может быть только прямое доказательство гипотезы.

Использованная литература

1. Хэйес, Брайан. Вздёты и падения чисел-градин. American. – 1984. – №3. – С. 102—107.

2. Стюарт, Иэн. Величайшие математические задачи. – М.: Альпина нон-фикшн, 2015. – 460 с.

3. Jeff Lagarias. The 3x+1 and its generalizations. American Mathematical Monthly. – 1985. – Vol. 92. – P. 3—23.

ОБЩЕЕ ПРЕДСТАВЛЕНИЕ ПОНЯТИЯ И ИСПОЛЬЗОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРИ ОПИСАНИИ НЕКОТОРЫХ ДИНАМИЧЕСКИЙ ЯВЛЕНИЙ

Алиев Ибратжон Хатамович

Студент 2 курса факультета математики-информатики Ферганского государственного университета

Ферганский государственный университет, Фергана, Узбекистан

Аннотация. Как некогда сказал Стивен Строгац: «Со времён Ньютона человечество пришло к осознанию того, что физики выражаются на языке дифференциальных уравнений». Разумеется, что данный язык используется далеко за пределами физики и талант использовать его, ровно, как и воспринимать, даёт новые краски при изучении окружающего мира. В настоящей работе описывается общее представление об этом методе и сам процесс его изучения.

Ключевые слова: дифференциальные уравнения, исчисления, алгоритмы, математическая физика.

Annotation. As Stephen Strogatz once said: «Since the time of Newton, mankind has come to realize that physicists are expressed in the language of differential equations.» Of course, this language is used far beyond physics and the talent to use it, exactly as to perceive it, gives new colors when studying the surrounding world. This paper describes a general idea of this method and the process of studying it.

Keywords: differential equations, calculus, algorithms, mathematical physics.

Сами по себе дифференциальные уравнения возникают каждый раз, когда описать изменение легче, чем абсолютные величины. Например, легче описать характер увеличения или сокращения роста или падения численности населения или популяции отдельного вида, чем описать те или иные значения в определённый момент времени. В физике, точнее в Ньютоновской механике, движение описывается благодаря силой, а сила определяется неизменной массой и меняющимся ускорением, что является утверждением об изменении.

Дифференциальные уравнения делятся на 2 большие категории – обыкновенные дифференциальные уравнения или ОДУ, включающие функции с одними переменными, чаще всего в лице времени и уравнения в частных производных с несколькими переменными. Если же уравнения в частных производных описывают более сложные характеристики, например изменение температуры в различных точках пространства, то обыкновенные дифференциальные уравнения описывают более статичные характеристики, изменяющиеся во времени.

В качестве не плохого примера можно рассмотреть процесс падения некоего объекта. Как известно, гравитационное ускорение равняется 9,81 м/с2, откуда получается, что если проанализировать положение тела в каждую секунду и перевести это состояние в векторы, то они будут накапливать дополнительную нисходящую 9,81 м/с2 ускорения каждую секунду. Это и даёт пример простейшего дифференциального уравнения, решением коего будет функция y (t), производная которой даёт вертикальную составляющую, а скорость даёт вертикальную составляющую ускорения (1).

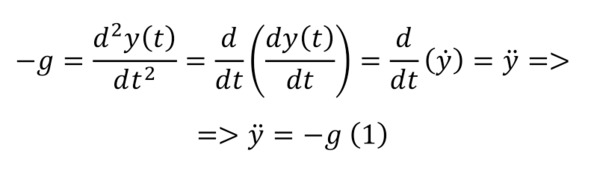
Это уравнение можно решить, выделив (2) для скорости и (3) для пути.

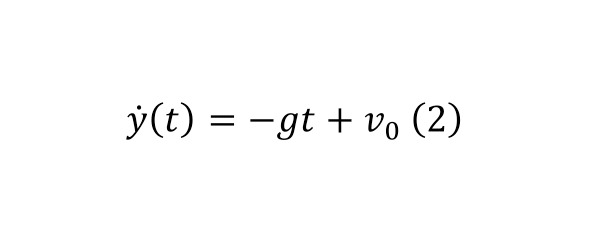
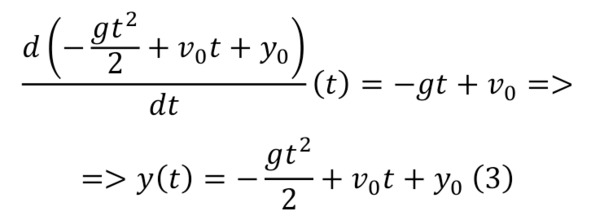
Интересен ещё тот момент, когда можно описывать движение небесных объектов в этом масштабе благодаря силе гравитации. Итак, даны два тела притяжение коего направлены в сторону друг друга с силой обратно пропорциональной квадрату расстояния между ними (4).

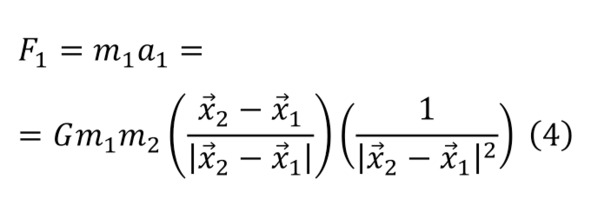
Известно, что производная координаты – скорость, производная скорости – ускорение и нужно получить функцию для движения, но по уравнению (4), известно только уравнение для ускорения (5).

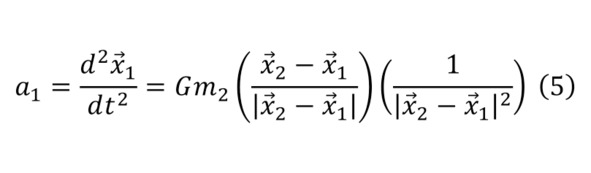
Здесь может быть странным, что производная равняется этой же функции, но это обычное явление, когда производная первого или высших порядков определяется значениями самих же себя. Но на практике, более часто приходиться работать с дифференциальными уравнениями второго порядка, как это можно увидеть и в предыдущих примерах.

Однако, существуют и дифференциальные уравнения с третьими (6) или четвёртыми (7) производными или более высокими (8) производными, что считаются дифференциальными уравнениями высшего порядка.

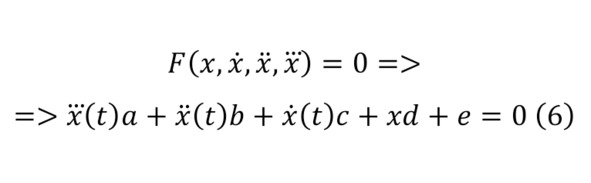
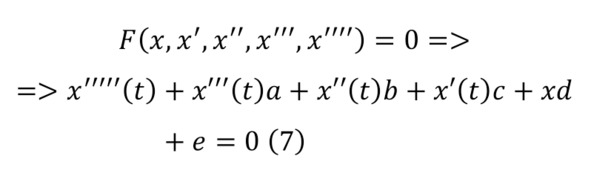
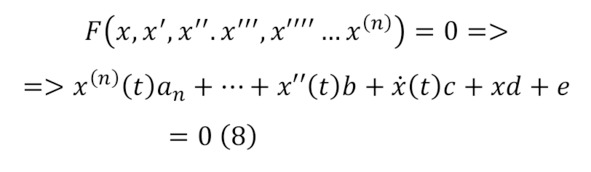
В некоем роде, получается, что нужно найти бесконечно много чисел, по одному на каждый момент времени, но в целом это и совпадает с описанием функции. И чаще всего, даже если во многих случаях можно применить классическое описание, то в большей мере использование технологии обычных математических преобразований уже не отвечают требованиям. Тому доказательством может случить обычное описание характеристики математического маятника.

Рассматривая реальный и идеализированный случай, можно отметить, что идеализация работает лишь на малых углах отклонения маятника, но когда же угол становиться достаточно большим, например равен полуокружности, то график описания его колебаний в целом перестают быть похожими на графики синуса или косинуса. Причиной тому является необходимость описания его движения исключительно при помощи не частных, а общих уравнений гармонических колебаний с дифференциальными уравнениями второго порядка.

Данную аналогию можно применить и для многих других физических, чаще всего реальных явлений.

Использованная литература

1. Потрягин Л. С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1974.

2. Тихонов А. Н., Самарский А. А. Уравнения математической физики. – М.: Наука, 1972.

3. Тихонов А. Н., Васильева А. Б., Свешников А. Г. Дифференциальные уравнения. – 4-е изд. – Фзиматлит, 2005.

4. Умнов А. Е., Умнов Е. А. Основы теории дифференциальных уравнений. – Изд. 2-е. – 2007. – 240 с.

5. Чарльз Генри Эдвардс, Дэвид Э. Пенни. Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. – 3-е изд. – М.: «Вильямс», 2007.

6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1969.

О ВОПРОСАХ ИССЛЕДОВАНИЯ ТРЁХКРАТНЫХ ИНТЕГРАЛОВ

Алиев Ибратжон Хатамович

Студент 2 курса факультета математики-информатики Ферганского государственного университета

Ферганский государственный университет, Фергана, Узбекистан

Аннотация. Изучение математической теории, способной в качестве отдельного инструмента описывать наблюдаемый мир весьма необходимо не только для исследователей в данной области, но и для всех представителей человеческой цивилизации, не говоря уже о тех, кто хочет производить описания математических теорий, ради этих же математических теорий. Особенной в данной части является такой метод исследования, как использование тройного или трёхкратного интеграла, наряду с отдельными операциями с элементами под знаком этого же тройного интеграла.

Ключевые слова: трёхкратные интегралы, математический анализ, исследования, определение, вычисление, научная новизна.

Annotation. The study of a mathematical theory capable of describing the observable world as a separate tool is very necessary not only for researchers in this field, but also for all representatives of human civilization, not to mention those who want to produce descriptions of mathematical theories for the sake of these same mathematical theories. Special in this part is such a method of research as the use of a triple or triple integral, along with separate operations with elements under the sign of the same triple integral.

Keywords: triple integrals, mathematical analysis, research, definition, calculation, scientific novelty.

Необходимость определения объёма, следовательно, исходя из плотности и массы, наряду с количеством составляющих и прочих производных от этих величин для объектов, которые невозможно определить практически, яркий тому пример определение массы горы, огромных деталей, для коих не представляется возможным или слишком затратным применение метода Архимеда, но необходимо вычисления объёма или даже при определении параметров целой планеты.

Объектом исследования является трёхкратный интеграл. Предметом исследования является процесс вычисления трёхкратного интеграла, а также оперирование с ним при замене переменных этого трёхкратного интеграла. В результате исследования выдвигается некоторая гипотеза, утверждающая о возможности использования трёхкратных интегралов при вычислении параметров линейных ускорителей относительно внутренних частиц гладких электромагнитных волноводов линейных ускорителей.

Целями исследования являются:

· Определение понятия трёхкратного интеграла;

· Исследование процесса замены переменных в трёхкратном интеграле;

· Показ модели вычисления параметров посредством трёхкратного интеграла для волновода линейного ускорителя.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.