
Полная версия
Все науки. №1, 2023. Международный научный журнал
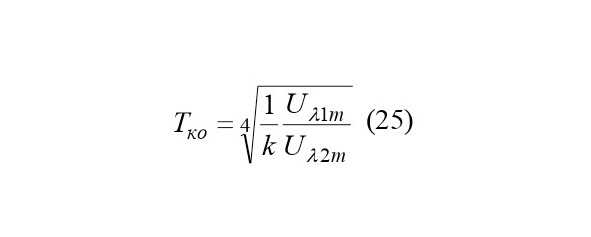
Таким образом, из последнего выражения видно, что температура в локальной фокусной зоне солнечных параболоцилиндрических концентраторов пропорциональна отношению напряжений Uλ1m и Uλ2m, которая регистрируется регистрирующим устройством, где учитывается.
Литература
1. Эргашев С. Ф., Кулдашов О. Х. Контроль концентрации газов в геотермальной энергетике. НТЖ ФерПИ, 2014.№3. с 105—109.
2. Далиев С. Х., Насриддинов С. С., Кулдашов О. Х. Использование светодиодов (1,94 µm) для измерения влажности хлопка-сырца. Материалы международной конференции «Oптические и фотоэлектрические явления в полупроводниковых микро- и наноструктурах». Фергана, 2020, С.426—427.
3. Кулдашов О. Х. Оптоэлектронное устройство для дистанционного контроля температуры бунтов хлопка – сырца. Международная конференция «Геоинформационное обеспечение аэрокосмического мониторинга опасных природных процессов». Иркутск, НИУ,2010.
4. Безъязычная Т. В., Богданович М. В., Кабанов В. В., Кабанов Д. М., Лебедок Е. В., Паращук В. В., Рябцев А. Г., Рябцев Г. И., Шпак П. В., Щемелев М. А., Андреев И. А., Куницына Е. В., Шерстнев В. В., Яковлев Ю. П. Оптоэлектронные пары светодиод-фотодиод на основе гетероструктуры InAs/InAsSb/InAsSbP для детектирования углекислого газа. Физика и техника полупроводников, 2015, том 49, вып. 7. С1003—1006.
5. Jha S. et al.«Violet-blue LEDs based on p-GaN/n-ZnO nanorods and their stability // Nanotechnology. – 2011, doi: 10.1088/0957—4484/22/24/245202.
МАТЕМАТИЧЕСКИЕ НАУКИ
ПОПУЛЯРНЫЕ В СОВРЕМЕННОЙ НАУКЕ ПАРАДОКСЫ МАТЕМАТИКИ
УДК 520.254
Алиев Ибратжон Хатамович
Студент 2 курса факультета математики-информатики Ферганского государственного университета
Арипова Сайёра Боходировна
Педагог общеобразовательной школы №1 города Фергана
Аннотация. В фундаменте математики есть слабое место, из-за чего нельзя знать всё наверняка, всегда будут истинные утверждения, которые нельзя доказать, никто точно не знает, что это за утверждения, но они похожи на гипотезу о «числах близнецах». Так пары простых чисел, где одна из них больше другого на 2, например 11 и 13 или 17 и 19. Если идти выше по числовой прямой простые числа встречаются всё реже, не говоря уже о таких парах. Но гипотеза о простых числах гласит, что их бесконечно много. До сих пор никто ещё не смог это доказать или опровергнуть.
Ключевые слова: математика, расчёты, дискретная математика, логика.
Annotation. There is a weak spot in the foundation of mathematics, because of which it is impossible to know everything for sure, there will always be true statements that cannot be proved, no one knows exactly what these statements are, but they are similar to the hypothesis of «twin numbers». So pairs of prime numbers, where one of them is larger than the other by 2, for example 11 and 13 or 17 and 19. If you go higher up the numerical line, prime numbers are becoming rarer, not to mention such pairs. But the hypothesis about prime numbers says that there are infinitely many of them. So far, no one has been able to prove or disprove this yet.
Keywords: mathematics, calculations, discrete mathematics, logic.
Но поражает то, что это вероятнее всего никто и никогда это попросту не сможет сделать. Ведь точно известно, что в любой математической системе, где определены операции, всегда будут истинные утверждения, которые невозможно доказать. Самым лучшим примером является математическая модель игры «Жизнь», созданная математиком Джоном Конвеем в 1970-м году.
«Жизнь» разворачивается на бесконечном поле из квадратных ячеек, каждая из которых либо «жива», либо «мертва», в игре всего 2 правила: любая мёртвая клетка, имеющая 3 соседей – оживает и любая живая клетка, у которой меньше 2 или больше 3 соседей – умирает. Так можно задать начальную конфигурацию расположения точек и модель создаёт первое, второе, третье и последующие поколения. Всё происходит автоматически хотя правила простые, они порождают довольно сложное поведение, где возникают следующие ситуации:
1. Стабильные состояния, которые застывают на месте;
2. Зацикливаются в бесконечной петле, постоянно мерцая;
3. Убегают в бесконечном поле, подобно глайдерам;
4. Попросту взаимно уничтожаются;
5. Живущие вечно и создающие новые клетки.
И смотря на такие условия хочется предположить, что любое поведение можно предсказать, придут ли они в покой или будут бесконечно расти в зависимости от начальных условий. Но как бы это не было странным, сделать это не представляется возможным. То есть нельзя создать алгоритм, который находил бы ответ за конечный промежуток времени, не выполняя сам алгоритм, до какого-то момента, но даже при этом, возможно говорить только о конечном счёте времени, то есть до какого-то числа поколений, а не о бесконечности.
Но что ещё более удивительно – это то, что подобные неразрешимые системы не единичны и явно не редки. Можно привести плитки Вана, квантовую физику, продажа авиабилетов или же карточные игры. Но чтобы понять, как возникает неразрешимость в этих случаях, придётся вернуться во времена XIX века, когда в математике и случился этот раскол.
В 1874 году немецкий математик Георг Кантор опубликовал свою работу, дав начало «Теории множеств». Множества – это точно описанное собрание чего либо, к которым можно отнести всё что угодно – обувь, планетарии мира, людей. Но среди таких множеств есть и пустые – в них попросту ничего нет, но также есть и множества содержащие абсолютно всё – это универсальные множества.
Но Кантора интересовали не сколько множества вещей, сколько множества чисел, а именно множества натуральных чисел – это все целые, рациональных чисел – все числа, которые можно представить в виде дроби, сюда же входят и целые, а также входящие в множество рациональных – множество иррациональных чисел – число «пи», Эйлера, корень из двух, а также любое другое число, которое можно представить как бесконечную десятичную дробь. Вопрос Кантора заключался в том, чтобы определить каких чисел больше – натуральных или вещественных в промежутке от 0 до 1. С одной стороны, ответ кажется очевидным – обоих по бесконечности, то есть множества равны, но для демонстрации этого была создана некоторая таблица.
Идея таблицы предельно проста – каждому натуральному числу пусть соответствует определённое вещественное число в промежутке от 0 до 1. Но поскольку это бесконечные десятичные дроби их можно записать в случайном порядке, но самое главное, чтобы присутствовали абсолютно все и не было ни единого повторения. Если же в результате лишних чисел не остаётся при проверке некой супермашиной, то получалось, что множества одинаковые.
И даже если допустить, что это так, Кантор предлагает придумать ещё одно вещественное число следующим образом. Он прибавляет к первой цифре после запятой первого числа единицу, затем единицу ко второй цифре второго числа, единицу третьей цифре третьего числа и т.д., если попадается 9 отнять единицу, и получившееся число находится всё в том же промежутке между 0 и 1, при этом ни разу не повторяясь во всём списке, ведь от первого числа оно отличается первым, от второго вторым, от третьего третьим и т. д. числами до самого конца.
То есть от каждого числа оно отличается как минимум одной диагональной цифрой, отсюда и название – Диагональный метод Кантора, который доказывает, что между 0 и 1 есть больше рациональных чисел, чем всех натуральных. Получается, что бесконечности могут быть разными, откуда и вытекают понятия континуума, а также счётного и несчётного множества. И признаться, эта работа стала не плохим стрессом для математиков того времени, ибо уже на протяжении 2000 лет считавшаяся идеальной Евклидова геометрия, итак, переживала трудные времена благодаря Лобачевскому и Гауссу, открывшие неевклидову геометрию, это приводило к плохому определению предела – основам математического анализа.
А теперь господин Кантор решил внести и свой вклад в эти процессы, показывая, что бесконечность гораздо сложнее чем казалось. Из-за этого разгорелись не малые споры, поделив математиков на 2 лагеря – интуиционистов, которые считали, что работа Кантора кошмарны, а математика – это изобретение человеческого ума, а Канторовы бесконечности не могут просто быть. К большому сожалению, к ним относился и Анри Пуанкаре, написавший: «Потомки прочитают о теории множеств, как о хвори, которую им удалось побороть», а Леопольд Кроникер называл Кантора учёным-шарлатаном и растлителем молодых умов. А также старательно мешал его карьере.
Им противостояли формалисты, которые считали, что теория множеств поставит математику на чисто логическую основу. И их не официальным лидером был немецкий математик Дэвид Гильберт, в то время ставший живой легендой, с работами практически во всех сферах математики, создав концепции, ставшие основой квантовой механики, и он прекрасно знал, что работа Кантора гениальна. Ведь такая идея, строгой и чёткой системы доказательств, опирающаяся на теорию множеств смогла бы решить все математические трудности, и многие с ним соглашались. Это также доказывают его слова: «Никто не сможет изгнать нас из Рая, который создал Кантор».
Но в 1901 году Бертран Рассел указал на серьёзную проблему в теории множеств, ведь если множество может содержать что угодно, оно также содержит и другие множества и даже себя. К примеру, множество всех множеств, должно содержать и себя, как и множество множеств с более чем 5-ю или 6-ю элементами или множество всех множеств, содержащих себя. И если это принять, получается странная проблема, ведь как поступить с множеством всех множеств, которые себя не содержат?
Ведь если это множество не содержит себя, оно должно содержать себя, а если оно не содержит себя, то по определению, оно должно содержать себя. Получается парадокс само-референции, где множество содержит себя, только если оно себя не содержит и не содержит себя, только когда содержит. Но более популярна его аллегория, с городом, где живут одни мужчины и брадобрей должен брить только тех мужчин, которые не бреются сами, но сам брадобрей тоже мужчина и там же живёт. Но если он не бреет себя, значит его должен брить брадобрей, но он не может брить себя, поскольку он не бреет тех, кто бреется сам, получается, он должен брить себя только если он не бреет себя. И разумеется, интуитивисты были рады этому парадоксу.
Но последователи Гильберта решили эту проблему просто изменив определение на то, что множество всех множеств – это не множество, как и множество множеств, которое не содержит себя. И хотя «битва» была выиграна, само-референция оставалась и ожидала своего реванша.
Эта проблема возродилась с 60-х годах XX века, когда математик Хао Ванг размышлял о способах разложения разноцветной плитки задав следующие условия – совмещать можно края одного цвета, но вращать или переворачивать клетку нельзя. И тогда встаёт вопрос, можно ли по случайному набору плиток сказать можно ли замостить всю плоскость? Получается ли это сделать до бесконечности и на удивление, эта задача стала не разрешимой, подобно игре «Жизнь» и вся проблема вновь свелась к уже знакомой само-референции, о которой ещё только предстояло узнать.
И тогда Гильберт решил создать надёжную систему доказательств. Основная идея такой модели была ещё в древней Греции, где какое-то изначальное утверждение принималось за истину без доказательств – аксиому, к примеру, то что между двумя точками можно провести только одну прямую и на основе этих утверждений строятся доказательства из следствий. Так получается сохранить истинность утверждений, где если верны исходные – верны и новые.
Так Гильберт хотел получить систему символов – язык со строгим набором операций, где математические и логические утверждения можно было бы перевести на этот язык, и фраза если бросить книгу – она упадёт сводиться к (1).
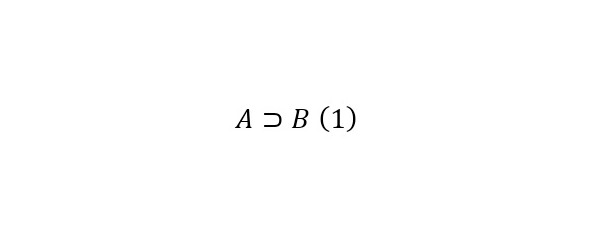
Которое читалось: «Если А, то В». А утверждение, что «Нет бессмертных людей» выглядела бы как (2).
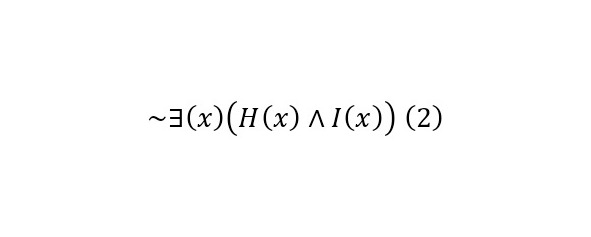
Так формалисты хотели придать математическим аксиомам форму символических утверждений и установить правило вывода в качестве математических операций в этой системе. Рассел вместе с Уайтхедом разложили и описали такую формальную систему в трёхтомнике «Принципы математики», опубликованная в 1913, ставший монументальным трудом в 2000 страниц плотного математического текста, где на 762 странице приводится доказательство, что 1+1=2, после чего констатируется, что «приведённое выше приложение иногда оказывается полезным» («The above proposition is occasionally useful»). Они планировали написать 4-й том, но кажется судьбе это не было угодно, говоря более образно и приводя не плохой пример.
Всё дело в том, что хоть такие математические записи слишком непривычны, но они кратки и точны, чем обычный язык, не оставляя место ошибкам или нечёткой логике, позволяя описывать свойства самой формальной системы. И если такая возможность наконец появилась, то это самое время для исследования самой математики, поставив три основных вопроса:
1. Полнота математики, то есть возможно ли доказать любое истинное утверждение?
2. Непротиворечивость, то есть свободна ли математика от противоречий? Ведь если можно сказать, что А – истинно и что А – ложно, одновременно, значит можно доказать что угодно и пропадает всякий смысл в самой науке.
3. Разрешимость математики, то есть ли такой алгоритм, который сказал бы – следует ли какой-то вывод из аксиом?
Гильберт был убеждён, что на все три вопроса можно ответить положительно, произнеся пламенную речь на конференции 30-го года, завершив фразой: «Пусть нашим лозунгом будет не ignorabimus, что значит „мы не узнаем“, а нечто совершенно иное: „мы должны знать – мы будем знать!“», эти слова и были высечены на его надгробии, но за день до выступления, на той же конференции, 24 летний логик Курт Гёдель рассказывал о том, что смог найти ответ на первый вопрос Гильберта о полноте и на удивление ответ был полностью отрицательным.
Неужели невозможно полностью сформулировать математику? И единственным, кто проявил интерес к юноше был Джон фон Нейман – бывший студент Гильберта, задавая различные уточняющие вопросы, после чего на следующий 1931-й год Гёдель опубликовал статью о неполноте и все, вместе с Гильбертом после этого обратили на него и его доказательство внимание.
А доказательство выглядело следующим образом. Он хотел использовать логику и математику, чтобы найти ответы на вопросы о том, как работают, логика и математика, для чего он взял все знаки математической системы и присвоил каждому из них свой номер, приводя нумерацию Гёделя.
Его система демонстрируется в (3—17).

Но если потратить на каждый знак числа, то для самих чисел, к примеру для 0 присваивается цифра – 6, а если написать 1, пишется «s0», что значит «следующее за 0», для 2 – ss0 и так можно выразить любое целое число, хоть и громоздко. Итак, если для обозначения и чисел ввели показатели, то можно записать и уравнения, к примеру «0=0», эти значениям присваиваются цифры 6, 5, 6, соответственно, но для уравнения «0=0», можно создать свою карточку, взять простые числа с 2 и они возводятся в степень числа элемента по системе Гёделя, а затем они перемножаются.
Так уравнение «0=0», записывается в (18).
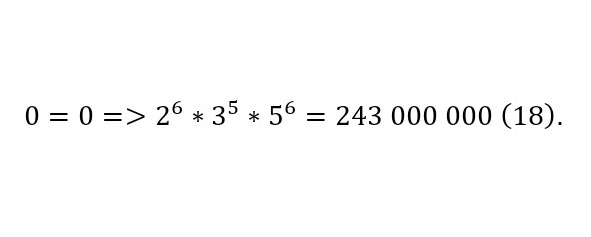
То есть, для уравнения «0=0», число Гёделя равно 243 000 000 и как можно видеть, подобные комбинации вполне можно получить для абсолютно любого уравнения, любой комбинации символов, и она словно бесконечная колода карт, где для любой комбинации существует персональная своя карта. А красота системы ещё заключается в том, что можно не только из уравнения получить число, но и из числа уравнение, для сравнения, можно взять любое число, попросту разложить его на простые множители, и в зависимости от степеней простых чисел получить уравнение.
Разумеется, что в этой колоде будут и истинные, и ложные утверждения, но для их доказательства, необходимо обратиться к аксиомам, которые тоже имеют свои номера Гёделя, к примеру, для аксиомы: «Нет любого числа за любым числом x, равным 0», ведь в этой системе нет 0. Записать такую аксиому можно в (19), а в (20), подставить под него 0, откуда следует, что 1=0.
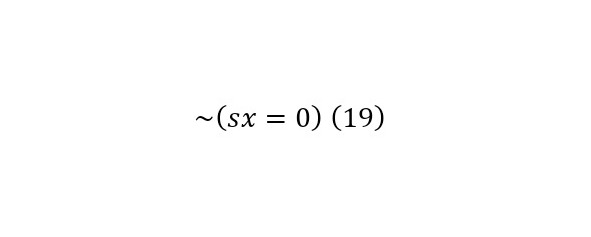
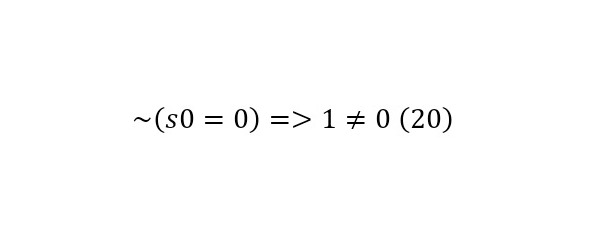
Именно так можно доказывать любое утверждение в системе Гёделя и конечно, это уравнение имеет своё число Гёделя (21).

Здесь два значения для доказательства и самой аксиомы разные. И как видно значения становятся всё больше и больше, поэтому просто необходимо ввести другие более ёмкие обозначения в виде букв, но получилось так, что для числа g, с уравнением (22):

доказательством стало само число g, то есть эти два числа совпали и получилось, что во всей колоде, нет ни одной карты, которая могла бы доказать такое утверждение. То есть если оно ложно и доказательство тому есть, то было доказано, что доказательства не существует. Это полный тупик, означающий противоречивость системы. Ведь даже если сказать, что это утверждение истинно, получалось бы, что есть утверждения, даже при наличии аксиом, что для них нет доказательств. И значит, система не полна, из этого следовало, что любая математическая система, способная к простым арифметическим вычислениям всегда будет содержать истинные утверждения, у которых нет доказательства.
Интересный тому пример приводится в цитате: «Джим мой враг, оказывается, что он злейший враг самому себе, а враг моего врага – мой друг, значит Джим – мой друг, но, если он враг самому себе, а враг моего друга мой враг, значит Джим – мой враг, но…» и эта череда может продолжаться бесконечно. И к сожалению, ответ на первый вопрос оказался отрицательным.
Если же вернуться ко второму вопросу, то непротиворечивость системы не может доказать сама же система, поэтому она остаётся под большим вопросом. И тогда разрешимость математики становится третьим вопросом, то есть существует ли алгоритм, который используя свои аксиомы точно покажет следующие из него утверждения? Решение вопроса было на стороне Алана Тьюринга в 1936-м году, для этого изобретя современный компьютер, хотя он хотел создать устройства с мощностью для решения задачи любой сложности с простым алгоритмов.
Он пришёл к мысли об устройстве, закреплённый на бесконечной ленте, с квадратными ячейками, содержащими либо 0, либо 1. Аппарат оснащён головкой чтения записи, за раз её считывая, а дальше может выполнить либо записать новое значение, перейти влево или вправо, либо остановиться. При этом остановка – это завершение программы, с выдачей результата. А программа – некоторый определённый алгоритм, указывающий машине, что делать и принимать какое решение, в зависимости от поступающей информации. Эту программу можно передать и на вторую машину Тьюринга, и она исправно будет её исполнять также как и первая, и это позволяет машинам выполнять всё что угодно, от сложения и вычитания, над сложнейшими алгоритмами современности, разрешая третью проблему Гильберта. Когда она останавливается – программа прекращается, а цифры на ленте – ответы.
Но порой можно вызвать случай, когда машина впадает в бесконечный цикл и тогда вопрос о том, можно ли зная исходные данные предсказать дальнейшее действие машины, становится весьма уместным. Тьюринг понял, что эта проблема не остановки похожа на проблему неразрешимости и, если понять, остановится ли машина, понять будет ли разрешима система не составит труда. Для примера можно взять гипотезу о числах близнецах, о которой говорилось ранее и тогда машина сформулировала бы при помощи аксиом все непосредственные вытекающие теоремы, построив все вытекающие теоремы, сравнивая каждую теорему из разных поколений, с гипотезой о числах-близнецах, это бы настоящая машина гениальности!
Решая проблему остановки, можно было бы решать всё и предсказывать всё что угодно и тогда Тьюринг решил сделать небольшую хитрость введя вторую машину, которая определяла бы остановку первой машины. То есть вводились бы исходные данные, описывался бы алгоритм машины и новая машина «б», выдавала бы, остановится или не остановится ли первая машина, при этом остановка через какое время уже не волновало, как и устройство обоих машин.
Но можно усовершенствовать эту машину «б», добавив к ней ещё два действия: если же первая машина остановится, пусть усовершенствованная версия машины «б» – машина «с» включит бесконечный цикл и, если выдаётся через внутренний «б», что «а» не остановится – остановку первой машины. Программу для новой машины можно задать как некий код, но что произойдёт если задать для неё этот же код и как алгоритм, и как код? Довольно интересный вопрос, получится что сама машина «с», симулирует как поведёт себя эта же машина «с», введя её собственной код, определив своё собственное поведение при каких-то обстоятельствах.
Тогда получится, что если каким-то образом машина «с» посчитает, что она никогда не остановится, она остановится, если она посчитает, что остановится, она никогда не остановится. Любые выходные данные получаются ложными и, следовательно, изначальной машины «б» попросту не может быть и невозможно предсказать, остановится ли первая машина Тьюринга «а».
Из этого следовало бы, что математика не разрешима, нет такого алгоритма, который выводил бы теоремы из аксиом самостоятельно. Но с одной стороны тут явно нет причины останавливаться или опускать руки, ведь все эти системы сами по себе полные, это означает, что они прекрасно функционируют, для примера вся современная вычислительная техника действует по принципу первой машины Тьюринга, но имеет слабое место в представлении самой же себя; квантовые системы полностью полны, но вопрос определения энергетических щелей или скорее вопрос неопределённости Гейзенберга или сводящиеся с ним вопросы также имеют слабые места; игра «Жизнь» также полна по Тьюрингу, но имеет слабое место – вопрос остановится ли игра или нет и таких систем огромное количество.
Ещё более удивительно то, что некоторые подобные системы можно создать в других, так в самой игре «Жизнь» можно создать машину Тьюринга, в которой уже запускается игра «Жизнь». Мечта Дэвида Гильберта относительно полноты действительно воплотилась в современных вычислительных машинах. И для него основной идеей стало: «Мы должны знать, и мы будем знать», но к сожалению, правда в том, что мы не можем знать, но в попытках разобраться, мы открываем новое, меняя наш окружающий мир, к примеру Тьюринг осуществил свои идеи во время Второй мировой войны, предугадав алгоритм работы машины «Энигма» фашисткой Германии, по некоторым оценкам, это приблизило конец войны на 2—4 года.
После войны Тьюринг и Джон фон Нейман создали первый программируемый компьютер «Эниак», на основе наработок Тьюринга, хоть он, к сожалению, не дожил до этих дней. Но он изменил наш мир, его называют самой влиятельной фигурой в кибернетическом мире, все его идеи до сих пор действуют в любой вычислительной машине, но они возникли в результате мысли о машине Тьюринга, а этому уже нужно сказать спасибо Гильберту и его вопросам о разрешимости математики, поэтому дешифровщики Тьюринга и вся компьютерная индустрия – плоды удивительных парадоксов в математике.
Поэтому в фундаменте математики по сей день имеется слабое место, из-за которого невозможно знать всё наверняка и будут утверждения, которые невозможно доказать, это обстоятельство могло бы свести математиков с ума и привести к краху дисциплины, но на удивление попытки решить эту проблему, изменили наше представление о бесконечности, переломили ход мировой войны и помогли создать устройства, которые способствуют развитию технологий сегодня.
И хотя это так, это по сей день служит для всех живущих и мыслящих ещё более лучшим знаком и намёком, а скорее утверждением, что нам нужно идти дальше, стараться развиваться, даже несмотря на то, что идеал недостижим…


