Полная версия
Частотный анализ числовых и текстовых данных. Учебное пособие

Частотный анализ числовых и текстовых данных
Учебное пособие
Валентин Юльевич Арьков
© Валентин Юльевич Арьков, 2023
ISBN 978-5-0059-8841-6
Создано в интеллектуальной издательской системе Ridero
Предисловие
Данная работа посвящена применению современных методов и технологий больших данных в курсе бизнес-аналитике и статистики. Анализ частоты появления различных значений – один из способов первоначальной обработки данных. Чаще всего его относят к описательной статистике (Descriptive Statistics). В последнее время также говорят об описательной аналитике (Descriptive Analytics). Подсчет частот имеет отношение распределению. Поэтому его восприятия материала желательно обладать пониманием основ теории вероятностей и математической статистики.
В данной работе мы рассмотрим примеры и приемы частотного анализа числовых и текстовых данных средствами Python.
К этому материалу следует относиться именно как к примерам. Потому что есть много способов выполнить одно и то же действие. Разные способы и разные алгоритмы могут дать в конечном счете один и тот же результат.
Данное пособие можно скачать совершенно бесплатно через сайт издательства Ридеро. Причем в разных форматах.
Введение
Частотный анализ – это изучение характеристик распределения случайной величины. Напомним, что распределение описывает вероятность (частоту) появления тех или иных значений статистического признака. Анализ формы и параметров распределения обычно относят к описательной статистике – Descriptive Statistics.
Язык Python во многом построен как объектно-ориентированный, поэтому мы имеем дело с объектами. А у объектов есть методы, которые соответствуют понятию функция и команда в традиционном программировании. Для упрощения мы будем говорить «функция», не углубляясь в технические подробности.
Мы будем выполнять работу в облачной среде Google Colab, но программу можно также использовать (с небольшими доработками) и в других средах. Основное преимущество Colab – это возможность приступить к работе, не занимаясь установкой программного обеспечения. Требования к компьютеру минимальные: наличие браузера и подключения к интернету.
1. Начало работы
1.1. Результаты и защита
Здесь мы обсудим первые шаги и основные моменты, касающиеся выполнения работы. В данной работе мы проводим обучение в режиме мастер-класса, когда студенты повторяют действия специалиста – «мастера своего дела». В данном выражении слово «класс» означает «занятия на выбранную тему». Это выражение позаимствовано из английского. Фактически, это английское выражение master class, записанное русскими буквами, а вовсе не перевод.
Программа на Python уже готова, её можно просмотреть, скачать и запустить. Мы обсуждаем её по частям, которые называются ячейками. Студентам нужно с этой программой ознакомиться и «поиграться», меняя некоторые параметры. В конечном счёте нужно достичь некоторого понимания и способности использовать и модифицировать эту готовую программу.
Поэтому в тексте даются пояснения и несложные задания. Во время защиты студент демонстрирует понимание материала и способность осмысленно использовать готовые команды и конструкции языка.
За счет такого подхода можно быстро войти в курс дела и сделать первые шаги в аналитике данных на Питоне.
Задание. Просмотрите в Википедии статью Мастер-класс.
1.2. Работа и отчет
Будем выполнять работу в облачном блокноте Jupyter Notebook в среде Google Colab.
https://colab.research.google.com/
Для работы понадобится подключение к интернет и учетная запись Google. Наш блокнот одновременно является инструментом для анализа данных и отчетом, в котором мы «документируем» все наши действия – шаг за шагом.
Для работы на локальном компьютере можно использовать бесплатную среду Anaconda с аналогичными возможностями.
https://www.anaconda.com/
Еще один вариант – это запуск на локальном компьютере контейнера с Anaconda и работа с ним через браузер.
1.3. Создание блокнота
При открытии страницы Colab выбираем создание нового блокнота: New Notebook. Задаём ему информативное название.
Блокнот состоит из ячеек, которые могут содержать программный код – Code — или текст – Text. Для создания очередной ячейки нажимаем соответствующую кнопку, см. рис.
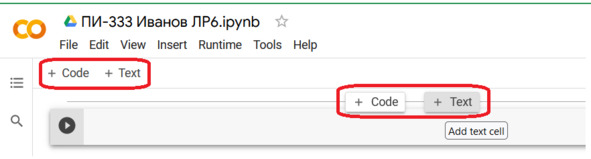
Рис. Создание ячейки
Отчёт по лабораторной работе традиционно начинается с титульного листа. В нашем примере это будет текстовая ячейка, содержащая основные данные о выполненной работе и исполнителе (студенте).
В начале каждого раздела создаём текстовую ячейку с соответствующим названием. Двойным щелчком левой кнопки мыши переходим к редактированию ячейки. Для заголовков первого верхнего уровня используем символ решетки. После ввода текста для «запуска» ячейки на выполнение нажимаем комбинацию клавиш [Shift + Enter]. При этом автоматически создаётся новая кодовая ячейка.
Чтобы раскрыть структуру документа, нажимаем кнопку содержание Table of contents, см рис.
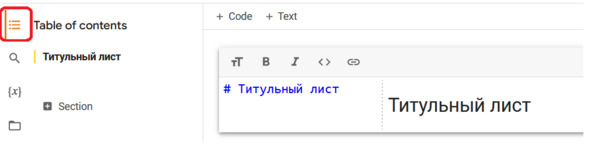
Рис. Заголовок раздела
Для оформления текста можно использовать разметку Markdown и HTML. При этом в правой половине ячейки открывается предварительный просмотр отформатированного текста, см. рис.
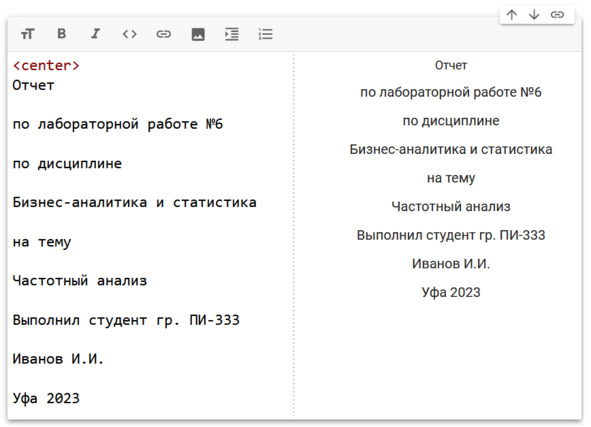
Рис. Титульный лист
2. Анализ числовых данных
2.1. Генерируем данные
В этой части работы мы познакомимся с возможностями анализа числовых данных.
Создадим новый раздел и озаглавим его: «Генерируем числовые данные». Обратим внимание, что мы можем перемещаться между разделами документа с помощью оглавления. Мы также можем сворачивать и разворачивать разделы, нажимая кнопку слева от заголовка раздела, см. рис.
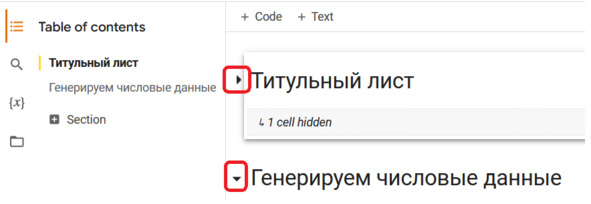
Рис. Управление разделами
Сгенерируем выборку, состоящую из случайных чисел с заданным распределением.
В начале импортируем загружаем библиотеку numpy – Numerical Python Extensions. Библиотека позволяет работать с числовыми массивами и содержит много полезных математических функций. Здесь же мы назначаем короткий псевдоним np для удобства вызова функций, см. рис.
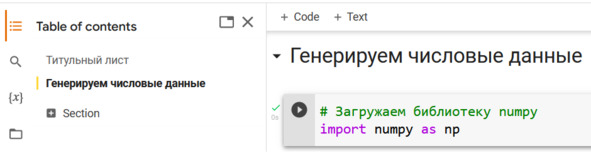
Рис. Загружаем библиотеку
По ходу выполнения работы вставляем комментарии. Это полезно и для себя, и для читателя. Комментарии начинаются с символа решетки #. Они сразу позволяют документировать ход работы. Так что у нас одновременно появляются и сама программа, и документация – описание к ней.
Зададим начальное состояние генератора случайных чисел. Вызываем функцию seed из встроенного модуля random. В качестве параметра укажем номер зачетной книжки, см. рис. Задавая одно и то же начальное состояние генератора, мы будет каждый раз получать один и тот же набор данных. На самом деле это псевдослучайные числа, которые получают путём вычислений. Внешне они выглядят как случайные.
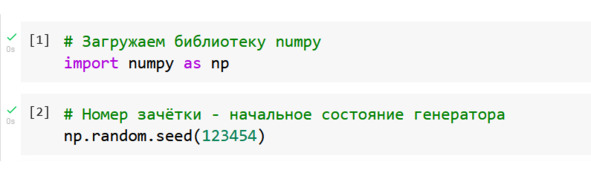
Рис. Инициализация генератора
После выполнения ячейки слева от неё появляется зеленый символ «галочка». Кроме того, в квадратных скобках указано число. Оно указывает, в каком порядке выполнялись ячейки. В блокноте Jupyter можно выполнять ячейки в любом порядке, причем можно запускать их много раз.
Во время работы с блокнотом советуем регулярно нажимать комбинацию клавиш [Ctrl + S] для сохранения. Блокнот сохраняется на вашем облачном диске Google Drive.
Теперь мы вызываем генератор случайных чисел и передаем ему параметры распределения и объем выборки, см. рис.

Рис. Генерируем выборку
Выводим на экран первые 10 элементов массива x. Мы не указываем начальный индекс, поэтому используется нулевой элемент. После символа двоеточия указан номер 10, но элемент с номером 10 не выводится. Мы увидим только элементы с номерами от нуля до девяти – это особенность Python.
При работе в блокноте нам не обязательно использовать функцию print. Достаточно указать имя переменной, см. рис.
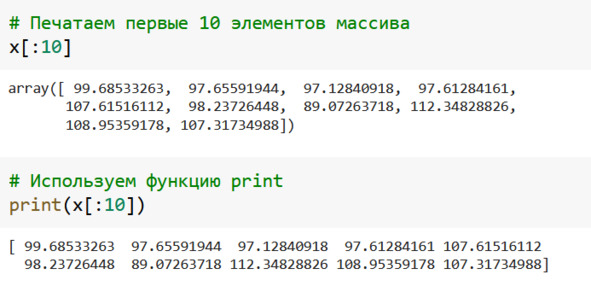
Рис. Начало массива
2.2. Гистограмма
Переходим к построению гистограммы.
Для создания графиков мы будем использовать библиотеку matplotlib. Из этой библиотеки мы загружаем модуль pyplot и назначаем ему псевдоним plt.
Теперь мы можем вызвать функцию построения гистограммы hist. В качестве параметра передаём имя нашего массива x. На экране появляется изображение гистограммы, причём количество интервалов группировки и их границы выбираются автоматически.
Над графиком выводится дополнительная информация: абсолютное частоты попадания в каждый интервал и границы интервалов группировки, см. рис.
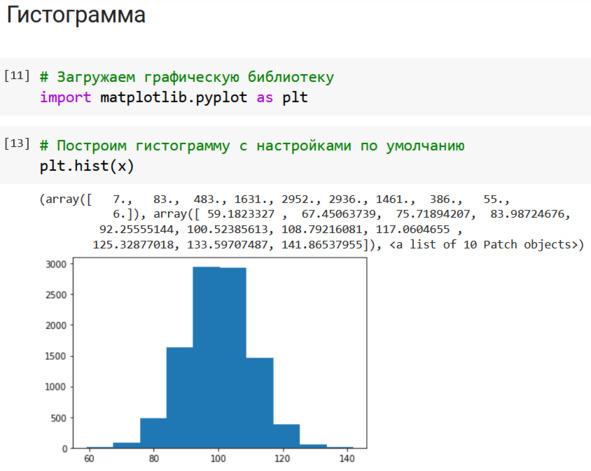
Рис. Гистограмма: настройки по умолчанию
При построении гистограммы мы не указали количество интервалов группировки. По умолчанию используется 10 интервалов. Чтобы задать другое значение, укажем параметр bins, см. рис. Нам нужно подобрать «приемлемое» количество интервалов – не слишком мало и не слишком много. Меняем значение n и запускаем нашу ячейку на выполнение.
Обратим внимание, что при вызове функций в Python мы можем передавать им параметры в любом порядке и даже можем их пропускать. Чтобы справиться с такими ситуациями, мы явно указываем название параметра, затем ставим знак равенства и даём его значение, например, bins=n.
Команда plt.show () подавляет вывод служебной информации на экран. В этом случае мы выводим на экран только сам график.
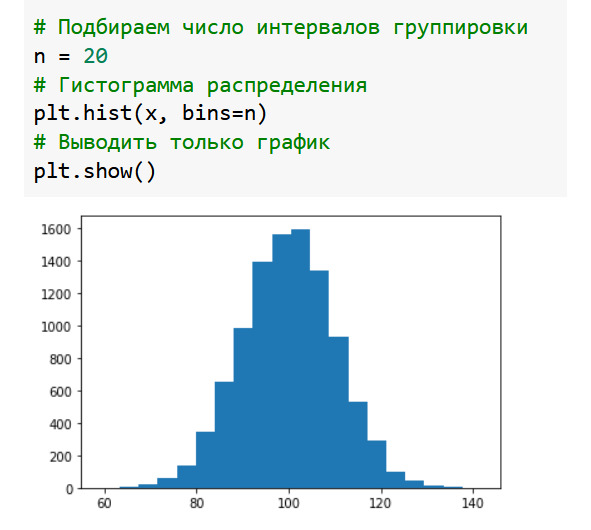
Рис. Настройка числа интервалов
Если задать слишком мало интервалов группировки, получается «грубая» картина с крупными «ступеньками», см. рис., слева. Слишком много интервалов дадут излишние подробности на графике – это просто случайный шум, за которым плохо просматривается форма распределения, см. рис, справа.
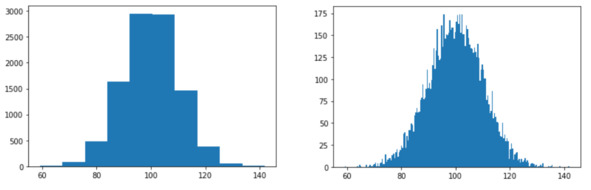
Рис. Подбираем число интервалов
Постепенно увеличиваем количество интервалов, пока не получим компромисс между грубыми ступеньками и случайными отклонениями. График должен получиться достаточно подробным, но не зашумлённым.
Теперь перейдём к оформлению графика, см. рис.
Настроим размеры изображения с помощью функции plt.figure (figsize= (12, 6)). Параметр figsize получает значения ширины и высоты изображения в дюймах.
Передадим дополнительные параметры функции plt. hist:
– edgecolor=’black’ – чёрные границы столбиков;
– linewidth=2 – толщина линий;
– facecolor=’white’ – заливка столбиков белым цветом;
– density=True – пересчитать результаты группировки как плотность вероятности.
Теперь площадь под графиком равна единице, и нашу гистограмму можно будет сравнивать с теоретической кривой нормального распределения.
Наконец, с помощью функции plt. title мы выводим заголовок графика.
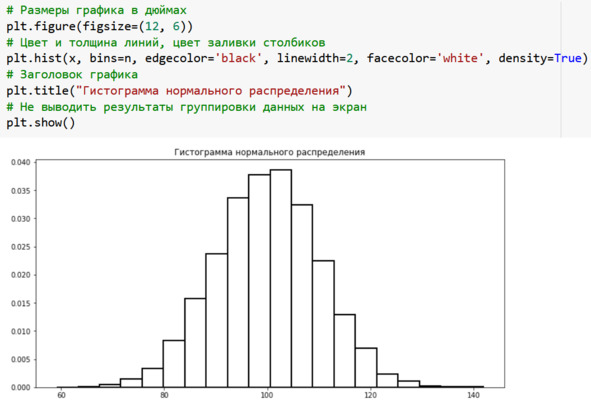
Рис. Оформление графика
2.3. Распределение
Рассчитаем теоретические значения плотности вероятности нормального распределения, см. рис.
Загружаем функцию нормального распределения norm из модуля stat библиотеки scipy.
Далее формируем одномерный массив (вектор) из 100 чисел в диапазоне от 60 до 140. В этих пределах расположена наша гистограмма. Для этого используем функцию linspace из библиотеки numpy.
Далее вычисляем значения плотности вероятности для нормального распределения с помощью функции norm. pdf. Название pdf в данном случае расшифровывается как probability density function – функция плотности вероятности. Задаем для этой функции те же параметры, что для генератора наших исходных данных:
– loc=mu – среднее значение (математическое ожидание);
– scale=sigma – стандартное отклонение («сигма»).
Здесь параметр loc означает location, то «расположение» среднего значения, то есть математического ожидания, которое обычно обозначается греческой буквой «мю».
Параметр scale определяет «размеры», или «размах» нашей кривой. Это среднее квадратическое отклонение, или С. К. О., или просто «сигма».
Строим график функции плотности с помощью функции plt.plot. Эта функция наносит на график точки и соединяет их прямыми отрезками. Поскольку точек и отрезков много, они сливаются и внешне выглядят как гладкая кривая.
Рассматриваем график и убеждаемся в правильности расчетов – обращаем внимание на среднее и разброс вокруг среднего (примерно три сигмы). В нашем примере это 100 плюс-минус 30, то есть от 70 до 130.
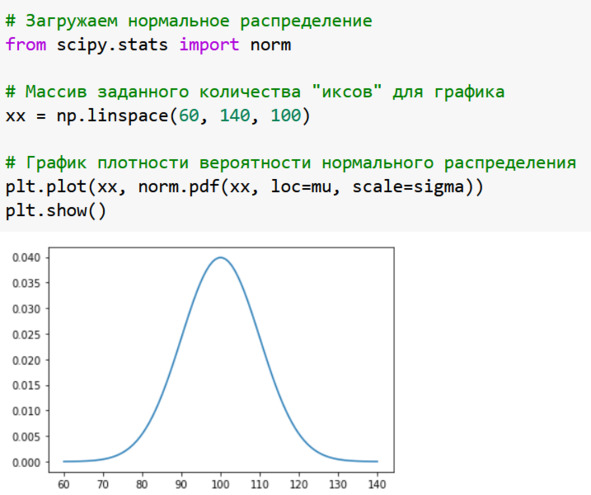
Рис. Плотность вероятности нормального распределения
Завершим оформление гистограммы – добавим теоретическую кривую и немного украсим изображение, см. рис.
При вызове функций plt. hist и plt.plot мы задаём параметр label. Это будет «метка» наших линий. Она нужна для оформления легенды, то есть вывода на график условных обозначений. Легенду мы выводим с помощью функции plt. legend () без параметров.
Для теоретического графика мы выбираем цвет с помощью параметра color. Линии разного цвета лучше воспринимаются, и эти цвета будут указаны в легенде.
Далее мы выводим заголовки по осям «икс» и «игрек»: plt. xlabel и plt. ylabel.
Наконец, на свободном месте графика выводим текст с помощью функции plt. text. Параметры этой функции следующие:
– x=130, y=0.033 – координаты левого нижнего угла текстового блока;
– s – строка текста для вывода на график (естественно, от английского слова string – строка).
Чтобы разобраться с этой строкой, придётся сосредоточиться. Итак, вначале указана буква f, что указывается на «форматированную строку», которая дана в кавычках. Далее мы выводим греческую букву «мю», для чего используем средства формул текстового редактора LaTeX: $\mu$. Формулы здесь вводятся в обрамлении символа «доллара». Затем мы выводим числовое значение переменной mu. Для этого используем фигурные скобки: {mu}. Затем используем символ перехода на новую строку \n – как и в стандартном формате вывода языка Си. Аналогично организуем вывод значения сигмы.
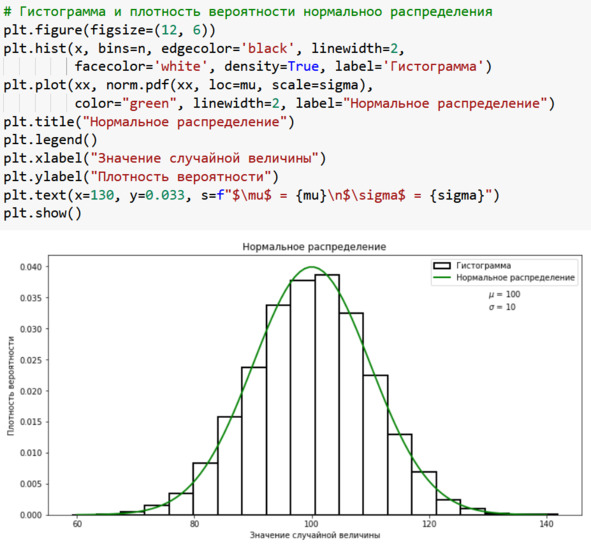
Рис. Оформление гистограммы
2.4. Полигон
Вместо гистограммы мы можем построить более гладкий график, который традиционно называется «полигон», то есть «ломаная линия». Дополнительно мы используем сглаживание, которое работает аналогично скользящей средней в динамике. Только здесь сглаживание работает по оси «иксов» вместо оси времени, см. рис.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.