Задачник о смысле жизни

Илья Галахов

Задачник о смысле жизни

«Никогда больше мы не будем просыпаться по утрам с мыслями "Кто я? В чём смысл моей жизни? А какое, в космических масштабах, будет иметь значение, если я не встану и не пойду на работу?" Ведь сегодня мы раз и навсегда узнаем простой и ясный ответ на все эти мелкие и докучливые вопросы Жизни, Вселенной и Всего на Свете!»[1]

Дуглас Адамс «Путеводитель для путешествующих автостопом по галактике»Задача 1

Время на стрелочных часах – 8 часов 36 минут. Какой угол в градусах образуют их стрелки в этот момент?

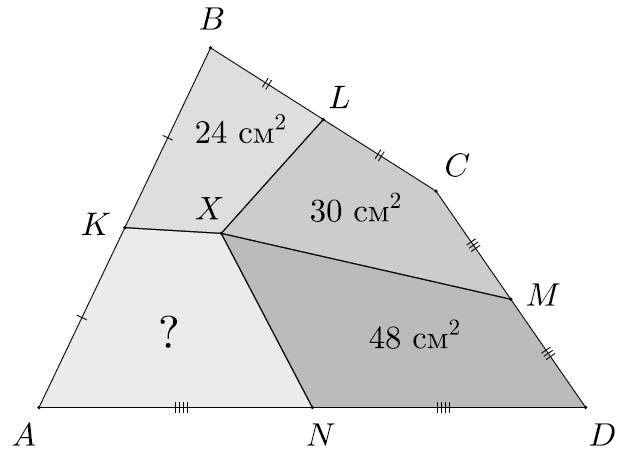
Задача 2

Внутри четырёхугольника ABCD выбрана точка X. Точки K, L, M, N – середины сторон AB, BC, CD, AD соответственно. Оказалось, что площади четырехугольников BLXK, CMXL, DNXM равны соответственно 24, 30, 48 см². Найдите площадь четырехугольника AKXN.

Задача 3

В некой стране 12 городов, и из каждого из них выходит по 7 дорог. Сколько всего дорог в этой стране?

Задача 4

Два велосипедиста едут навстречу друг другу. Один велосипедист проезжает 19 км в час, а другой 23 км в час. Какое расстояние будет между ними за час до встречи?

Задача 5

Угол A ромба ABCD равен 96°, E – середина AB, F – основание перпендикуляра, опущенного из D на CE. Найдите угол BFE.

Задача 6

Сумма семи последовательных чисел равна 315. Чему равно наименьшее число?

Задача 7

В хранилище банка X имеется 100 квинтиллионов монет (10²⁰ монет). Среди них оказалась одна фальшивая монета, которая легче настоящих. В банке есть огромные чашечные весы, одно взвешивание на которых занимает 1 минуту. За какое минимальное время сотрудники банка гарантированно могли обнаружить фальшивую монету?

Задача 8

Сын в 3 раза моложе отца. Когда отцу было 33 года, сыну было 5 лет. Сколько лет отцу?

Задача 9

В трапеции ABCD с основаниями BC и AD диагонали пересекаются в точке X. Найдите основание AD, если DX: BX = 7:3, BC = 18.

Задача 10

Одно из двух натуральных чисел заканчивается цифрой 1. Если эту цифру зачеркнуть, получится второе число. Найдите его, зная, что сумма этих чисел равна 463.

Задача 11

Илья задумал двузначное число, разделил его на 7, прибавил 29, зачеркнул последнюю цифру, результат умножил на 14 и снова получил задуманное число. Какое?

Задача 12

На столе лежат 6 кучек камней, в каждой кучке 8 камней. Таисия и Дима играют в игру – разбивают кучки на меньшие. За ход разрешается разбить любую кучку на две. Проигрывает тот, кто не сможет сделать ход. На каком по счёту ходу закончится игра?

Задача 13

Семье туристов нужно перебраться сквозь узкий и тёмный лаз в горе. Папа может сделать это за 2 минуты, мама – за 3, брат – за 7, сестра – за 9, дедушка – за 11, а бабушка – за 14 минут. Проходить можно только с фонариком, и не более чем вдвоём в одном направлении (двое двигаются с меньшей из их скоростей). Фонарик есть только один. За какое наименьшее время все туристы смогут перебраться через лаз?

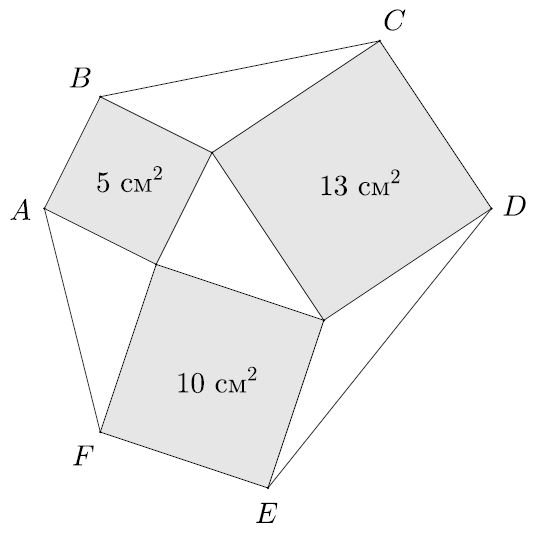
Задача 14

Три квадрата, площадями 5, 10 и 13 см² попарно имеют общие вершины, как показано на рисунке. Вершины квадратов, не являющиеся общими, образуют шестиугольник ABCDEF. Найдите его площадь.

Задача 15

На доске написано число 1111117225493, в котором можно стереть несколько цифр (не все). Сколько разных чисел, кратных 5, возможно получить таким способом?

Задача 16

Из пунктов A и B, расстояние между которыми 18 км, одновременно навстречу друг другу выехали велосипедисты: из пункта A со скоростью 13 км/ч и из пункта B, находящегося на горе, со скоростью 17 км/ч. В тот же момент из пункта A вылетела муха и стала летать между велосипедистами. Долетев до одного из велосипедистов, она разворачивалась и летела к другому, долетев, снова разворачивалась и летела обратно и т. д. Скорость мухи 70 км/ч. Какое расстояние пролетела муха до того, как велосипедисты встретились?

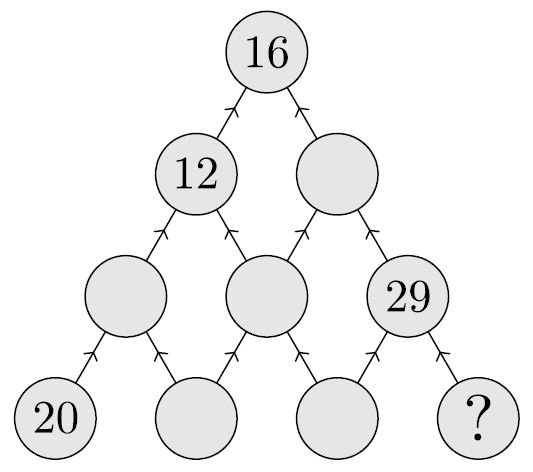
Задача 17

В кружки на рисунке записали среднее арифметическое над каждыми двумя соседними числами, а потом часть чисел стёрли. Какое число было в правом нижнем кружке?

Задача 18

На прямой последовательно расставлены точки A, B, C, D, E. Сумма расстояний от A до остальных четырёх точек равна 197, а сумма расстояний от B до остальных четырёх точек равна 71. Найдите расстояние от A до B.

Задача 19

В таблице 3x3 числа были расставлены так, что их суммы по всем строкам, столбцам и двум главным диагоналям равны. Затем часть чисел стёрли, как показано на рисунке. Найдите, чему равно число в левом верхнем углу таблицы.

Задача 20

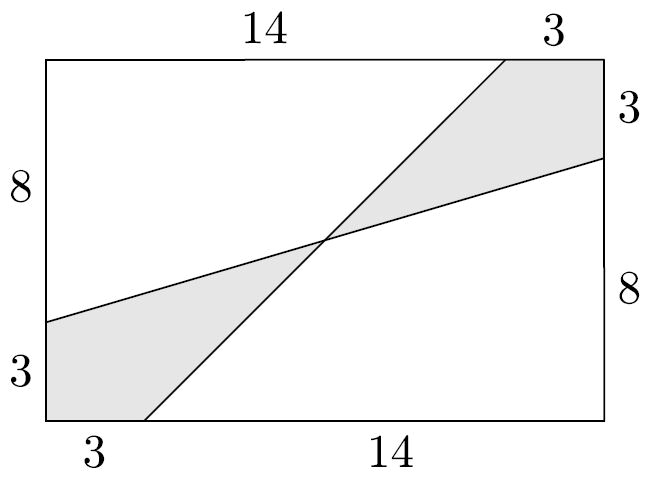
Дан прямоугольник 11x17. Чему равна площадь закрашенной фигуры?

Задача 21

Часы бьют 6 раз за 5 целых и 5/6 секунды. Сколько градусов пройдет секундная стрелка, пока часы бьют 7 раз?

Задача 22

В трапеции ABCD угол ABC равен углу ACD, основание BC равно 28, а основание AD равно 63. Чему равна диагональ AC?

Задача 23

В правильном 30-угольнике A1A2…A30 (вершины расположены именно в таком порядке) проведены диагонали A5A13 и A7A18. Чему равен угол между ними?

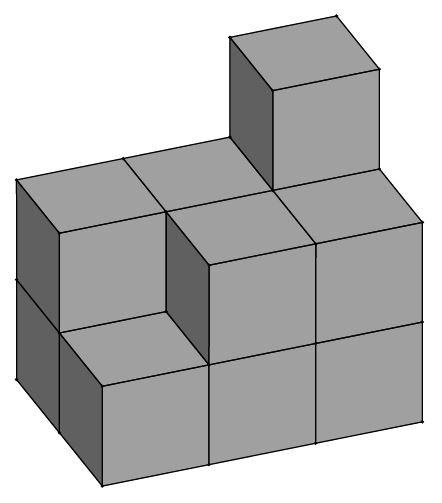
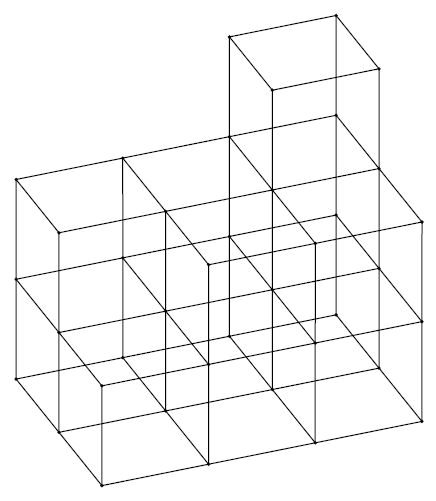
Задача 24

В фигуре на верхнем рисунке оставили только рёбра, как показано на нижнем рисунке. Какое максимальное количество рёбер можно убрать, чтобы все вершины остались связаны между собой?

Задача 25

Три белки в лесу прыгнули по очереди с ветки на ветку. Каждая приземлилась точно в середину отрезка между двумя другими. Длина прыжка второй белки 84 см. На какое расстояние прыгнула третья белка?

Задача 26

В марте у Кати в дневнике стояло 17 двоек и 8 троек по алгебре. В апреле она подтянулась и начала получать только пятёрки. Сколько пятёрок нужно получить Кате, чтобы её средний балл стал в точности равен 4?

Задача 27

Ребёнок становится счастливым, когда получает три разные конфеты. Какое наибольшее количество детей может осчастливить Дед Мороз, имея в мешке 23 помадки, 27 ирисок, 34 коровки и 49 леденцов?

Задача 28

Сумма тринадцати различных натуральных чисел равна 120. Какое максимальное значение может быть у наибольшего из этих чисел?

Задача 29

Каким наименьшим числом монет в 5 и 7 копеек можно набрать сумму 2 рубля 90 копеек?

Задача 30

В музее странных вещей представлена рукопись, в которой написано 43 следующих утверждения:

«В этой рукописи ровно 1 неверное утверждение».

«В этой рукописи ровно 2 неверных утверждения».

. . . . . . . . . . . . . . . . . . . .

«В этой рукописи ровно 43 неверных утверждения».

Сколько на самом деле неверных утверждений в этой рукописи?

Задача 31

При обычной стирке бельё стирается за 39 минут, а при бережной – за 1 час 31 минуту. Игорь запустил стиральную машину сначала в режиме бережной стирки, а через некоторое время передумал и переключил режим на обычную стирку до её окончания. Найдите общее время стирки, если известно, что в режиме обычной стирки стиральная машина находилась семь восьмых от общего времени стирки. Считайте, что и при обычной, и при бережной стирке бельё очищается равномерно.

Задача 32

Между цифрами двузначного числа вставили ноль, и к полученному трёхзначному числу прибавили удвоенную цифру его сотен. Получилось число, на 10 меньшее числа, в 10 раз большего первоначального. Найдите исходное число.

Задача 33

Площадь клетчатого прямоугольника равна 68 клеткам. Его раскрасили по клеткам в чёрную и белую полоску. Оказалось, что количество полосок одного цвета отличается от количества полосок другого цвета. Чему равен периметр прямоугольника?

Задача 34

Первый жираф ниже второго на 29 целых и 41/71 процента. На сколько процентов второй жираф выше первого?

Задача 35

В мешке лежат 14 красных, 15 чёрных, 10 белых, 5 зелёных и 23 синих шара. Какое наименьшее количество шаров необходимо вытащить из него вслепую так, чтобы среди них точно нашлось 10 шаров одного цвета?

Задача 36

На стороне BC треугольника ABC выбрана точка D. Известно, что AB = 39, AC = 53, BD = 27, DC = 19. Чему равно AD?

Задача 37

У Владимира Викторовича есть двое брюк, три кофты и шесть галстуков. Сколькими способами он может составить костюм? (Все предметы обязательны, кроме галстука.)

Задача 38

Четырёхугольник ABCD вписан в окружность. Касательные к этой окружности, проведённые в точках A и C, пересекаются на прямой BD. Найдите сторону AD, если AB = 9 и BC: CD = 3:14.

Задача 39

Обозначим через S(x) сумму цифр натурального числа х. Решите уравнение: x+S(x)+S(S(x))+S(S(S(x)))=60

Задача 40

В треугольнике ABC на стороне BC отмечена точка P так, что сумма углов BAP и BAC равна 180°. На стороне AB отмечены точки Q и S такие, что углы BPS и APQ равны 53°, а угол ACQ равен 11°. Чему равен угол PSC?

Задача 41

В международном форуме участвует 87 человек. Из них 23 человека говорят по-английски, 19 – по-французски, 27 – по-испански. Английский и французский знают одиннадцать человек, английский и испанский – девять, французский и испанский – семеро. Три человека говорят на всех трёх языках. Сколько участников форума не знают ни одного из этих языков?

Задача 42

Найдите площадь фигуры на рисунке (размер клетки 1x1):

Написать автору можно по электронной почте.

Примечания

1

Дуглас Адамс. Путеводитель для путешествующих автостопом по Галактике. М.: АСТ, 2022.