Probabilistic Theory of Stock Exchanges

1.2. DIRECT AND INVERSE PROBLEMS OF ECONOMIC THEORY

To develop a probabilistic theory of the exchange, a physical method of economic research was used, the essence of which consists in using standard theoretical approaches of physics for modeling and calculating economic systems, with subsequent constant comparison of calculation results with experimental data to verify the used approaches, models and theory as a whole and for the purpose of establishing thereby the applicability limits of models and theory as a whole in those cases where their improvement and development is feasible. If the results of calculations contradict the experiment to a sufficient degree, the theory should be rejected without hesitation, and the process of theory creation should be started anew. For the sake of certainty and clarification of the theoretical problems studied in this book, we further call this option of the physical method application “a solution of the direct problem of the economic theory”, in which the results of economic activity (in this book, stock trading) are calculated based on some initial principles (ab initio principales), which are then compared with the corresponding experimental data (in our case – with the results of stock trading). We oppose this approach to solving, shall we say, the inverse problem of economic theory, in which by mathematical processing of experimental data one seeks to obtain information about the studied economic system. It should be said that we borrowed the terms "direct and inverse problem" from the theory of elementary particles scattering, which solves formally similar problems. It is known that solving the inverse problem in physics is very difficult and there is no reason to think that solving the inverse problem in economics will be easier. Here we reserve to developing the methods for solving the direct problem of economics as applied to stock exchanges, so all conclusions and discussions in this book refer only to the direct problem of economic theory, unless specifically stated. In order to avoid misunderstandings, we will repeatedly emphasize this aspect of this study.

It seems to us that one of the results of the extensive application of the physical method to the research of economic problems by solving the direct problem of economics will be the development of a new interdisciplinary science "physical economics", the birth of which is taking place right before our eyes. At present, physical economics is developing quite intensively in different directions, and one of these directions is probabilistic economic theory, the simplest, one may say, starting version of which is the probabilistic economics considered in this paper; and it is the latter that served as a basis for the probabilistic theory of stock exchanges. The main advantage of this approach is the availability of methods for solving the direct problem of economics, namely numerical calculations based on the first principles of such parameters and functions that can be directly compared with Experimental data, in our case – with the experimental results of real-time exchange trading.

According to the new physical method of thinking and research in economics, which we share and develop, in this monograph as well, the main requirement to such economic models, defining their main purpose, is the possibility and, to some extent, even art, with a few important axioms, concepts and principles to harmoniously, competently and simultaneously include them in the theory. The latter is very important, since, by the definition of the purpose, all concepts and principles play certain roles of comparable importance in the studied economy. And of course, constant verification of the assumptions made, concepts and the theory itself through numerical calculations and comparison with experiment data is necessary. It is this emphasis on experimental verification of theories that distinguishes the physical method from all other approaches, including neoclassical theory, which is currently mainstream in economics. In other words, the physical method of economic research presupposes a constant reliance on experiment, as it is usually the case in physics: numerical solutions of a direct problem are compared with the corresponding experimental data. We are fully confident that due to its naturalness and obviousness, in the nearest future the physical method will become the main method of economic research, will be called simply a scientific method of economic research, so the necessity to call it a physical method in economics will disappear due to irrelevance and unnecessity.

1.3. CONCEPTUAL MODELING OF ECONOMIC SYSTEMS IN PQ-SPACE

It is well known that the method of conceptual modeling of economic systems has long been widely used in economic theory. For example, the first and most famous concepts of neoclassical economics are S&D concepts. It is due to them that neoclassical theory has made a significant contribution to economic science. It helped economists better understand the basic components of the economic world, and with the help of a graphical interpretation this knowledge became more accessible to those interested in these issues, in particular students. In Austrian economics, the so-called method of ideal or imaginary constructions rightfully occupies one of the central places [Mises, 2005].

It is not customary in theoretical physics to emphasize the use of models, since theoretical physics itself can rightly be viewed as a conceptual mathematical modeling of physical systems. In particular, theoretical physics has developed the most advanced methods of theoretical modeling of complex systems. Moreover, here it has long been implicitly required from the researcher to perform quantitative numerical calculations of the structure and properties of such models with the highest possible accuracy, which, in turn, led to a striking development of quantitative methods in quantum mechanics of multiparticle systems, especially in quantum chemistry of multi-atom systems [Kondratenko and Neyman, 1990].

So, in this study deep structural and dynamic analogies between physical multi-atom systems and multi-agent economic systems are used in order to transfer conceptual, analytical and numerical methods from theoretical physics to theoretical economics. This transfer is performed by means of physical modeling of economic systems or, in short, physical-economic modeling. Our concept of physical-economic modeling is based on the well-known fundamental ideas of classical economic theory, first of all of Austrian economics. They are then combined and eventually, with the help of additional concepts and mathematical body adopted from physics, transformed into a new economic theory. This combination is organized through formal approaches and methods borrowed from theoretical physics, starting from the introduction into economic theory of the formal economic space concepts, motion trajectories of market agents and the market as a whole in such space, and finishing with the substantiation of the principal possibility of using the method of equations of motion in economic theory. To avoid misunderstandings, we emphasize again that the role of theoretical physics here is only to provide the mechanisms for developing a probabilistic economics. Relying on this theory, step by step, taking into account all principles of the theory simultaneously, we create more complex physico-economic models, taking into account the experience with previous models, which will be repeatedly illustrated in figures and graphs.

Of course, all physical-economic models are essentially conceptual mathematical models, just as in physics. The notion of "physical modeling" is used to emphasize an analogy with the rules or principles of modeling in physics. Further, this term will become redundant and will not be used. In the course of developing conceptual models of economic systems we will consistently introduce the concepts and principles of our theory, which will serve as a basis for the models’ frameworks, which, in turn, will be filled with new content step by step. We will start with constructing the simplest models with the help of analogies and formal methods of classical mechanics. For the sake of brevity, we will call such models classical models below. Naturally, only the first five principles will be used in the development of such a classical theory, or simply classics, since only they have analogues in classical mechanics.

So, Fig. 1.1 shows a typical graphic economic model of a market system, or simply, a market. This model, configured by analogy with models for physical multiparticle systems, uses a number of legends or conventions to demonstrate typical market structure.

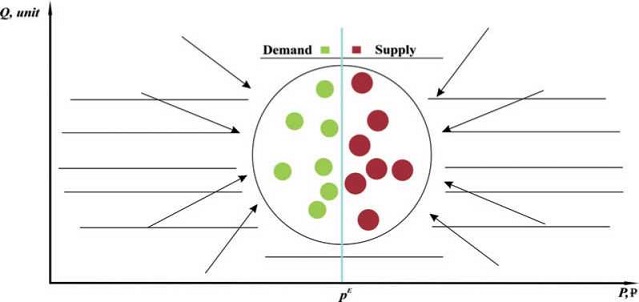
Fig. 1.1. Graphical model of a single-commodity multiagent market economy in the economic two-dimensional price-quantity space. The dots inside the conventional sphere represent market agents: buyers (green dots) and sellers (red dots), forming demand and supply, respectively. The sphere is divided into two parts by the narrow blue line, which symbolically marks the narrow area of prices, where the transactions in the market are made at the current experimental price pExp. Buyers are in the left hemisphere and sellers are in the right hemisphere, since the buyers’ prices are lower than the sellers’ prices with very rare exceptions.

The main structural element of the model is the market itself, consisting of a certain number of interacting market agents: buyers and sellers. This market is not a closed system – it is an open system, because it is under the constant influence of its institutional and external environment, as well as other markets and other sources of influence. All these factors also serve as structural elements of the market, because they exert a strong influence on market agents, and without taking it into account it is impossible to obtain a reliable description of the mechanisms of market operation and its results.

Further, in order to be able to mathematically describe the dynamics of the economy, we should, just like in physics, place the entire market into some constructed economic spaces. Since such economic spaces, in contrast to the physical space, have an auxiliary and formal character, they can be constructed in different ways depending on the tasks to be solved. In this paper, it is appropriate to use the price-quantity space corresponding to two sets of independent variables, prices P and quantities Q for all traded goods on the market (PQ-space). For clarity, we denote the names of independent variables and their corresponding coordinate axes in bold. Despite its seeming simplicity, the concept of multidimensional economic space introduced in this study is of great importance in theory, since it provides a fundamental opportunity to describe the dynamics of economic systems in mathematical and graphical languages, as it has long been accepted in science.

This paper will extensively use the notion of "market structure", which includes both the agent structure of the market itself and all significant external factors and forces of various nature that affect the operation of the market. The study of the market structure and its various microstructures and the identification of the most important characteristics and connections between them represents the most important purpose of any economic theory.

The approach of probabilistic economics, aimed at solving the problem of adequate quantitative description of each agent’s behavior in the market, as well as the behavior of the market as a whole, is based on one rather simple premise or hypothesis, which we will call an axiom. This axiom, which has a rather general character, forms the basis for the implementation of supply and demand concept in a probabilistic economy.

1.4. AXIOM OF AGENT IDENTITY

All market agents are identical, only their supply and demand are different. This axiom is the starting point in building up the theory. It says that in the context of studying the basic or determinant features of the behavior of market agents in the market and the market as a whole, especially in terms of the formation of market prices and trade volumes, all market agents have common or identical properties, depending mainly on the income and expenditure of agents, or, more precisely, on their S&D for the goods and services produced and traded in markets. In other words, all buyers with the same demand are identical, just as all sellers with the same supply are identical. It can also be said that such agents are indistinguishable from the point of view of influencing the outcome of market trading or exchange. This axiom is something similar to the principle of indistinguishability of particles in physics, but, naturally, it is not as strict as the principle of indistinguishability in physics. It is the S&D of agents that primarily determine their economic behavior in markets and, ultimately, the behavior of all markets; they are the only characteristics of agents and the main input data for calculation methods in probabilistic economics, i.e. the parameters that determine the studied economic system.

This axiom points to the possibility of constructing sufficiently generalized and accurate models of the agents’ behavior in the market and, consequently, of the market as a whole on the basis of agents’ supply and demand. It leads us to the right path for determining and defining general properties of the market agents’ behavior, which, in turn, enables us to identify general regularities in the course of market processes. This gives us a reliable basis for building theoretical economic models at a fairly high scientific level, using formal physical and mathematical methods. We are convinced that only these types of general market phenomena and processes fairly represent the main interest of any sufficiently accurate scientific investigation using the methods of theoretical and experimental economics. In other words, this axiom forces us to focus on building the economic theory as a sufficiently rigorous science, based on the study of the behavior of individual agents (see the principle of methodological individualism [Mises, 2005] in terms of their S&D, i.e., behavior determined by their individual demand or supply.

To avoid misunderstandings, let us make the following note. Of course, there are many aspects of the economic agents’ behavior in markets, which are determined by specific nuances and peculiarities in the behavior of particular people and communities in different situations and in different markets, and which often cannot be described in terms of supply and demand. These nuances and peculiarities of specific economic agents in particular markets are important, of course, when studying the process of making specific market decisions in particular situations of planning their market intentions and strategies [Schiller, 2000], for example, when choosing their quotations in course of trading at an exchange, but they are not the subject of probabilistic economics in this study. Moreover, for a probabilistic economics, it is all these nuances and features that determine the supply and demand for each agent at any given time, and these S&D are the inputs to the probabilistic economics. But, again, neither these nuances and peculiarities, nor concepts such as expected utility and risk [Wickens, 2012], are the basic concepts or the subject of research in probabilistic economics. The same is true for the nuances and peculiarities of exchange markets: in probabilistic theory, there is no need to describe and explicitly account for them, unlike in traditional theories like efficient market theory [Fama, 1970]. After all, it is not all these specific nuances and peculiarities of decision-making processes of market agents, and not the properties of specific markets like perfect competition, etc., but the specific actions of market agents and their determining role in the operation, development and evolution of markets, and the economy as a whole, that constitute the main subject of research and the main content of economic theory, in our opinion. As we argued above, it is, of course, important to understand what market agents think, and why they make these particular decisions, and not others, but, nevertheless, this is the subject of research in other more applied disciplines of economic science.

1.5. PRINCIPLES OF PROBABILISTIC ECONOMICS

As we know, specific definitions of supply and demand as well as formulations of the S&D concept and methods of building S&D functions differ from each other in each economic theory, depending on its goals, objectives and possibilities. For example, the concept of supply and demand in mainstream neoclassical economics is based on the intentions or action plans of market agents. The intentions or plans of market agents are a trade secret, but it is completely impossible to build up a quantitative economic theory on the basis of the unobservable intentions or plans of real market agents. On the contrary, probabilistic economics is built on the basis of real actions of these agents in markets that can be observed and measured. More precisely, in a probabilistic economics, market S&D are derived or result from real agent S&D, i.e. from real agent market actions. In this fundamental point, by the way, probabilistic economics is close to the Austrian school of economics, especially in the interpretation of Ludwig von Mises [2005]. In other words, unlike, say, neoclassics, the probabilistic functions S&D are determined on the basis of the real actions of market agents in the market. And they are calculated with strict account of the following six principles of probabilistic economic theory.

1.5.1. SUPPLY AND DEMAND PRINCIPLE

Probabilistic economics is based on the most well-known concept of economic theory, namely the concept of S&D. In its most general form, this concept is formulated in probabilistic economics as follows: all the main things that happen in the market depend on some specific balance of supply and demand, determined on the basis of decisions made and openly presented in the form of market orders or market quotations to buy or sell a certain amount of an asset at a certain price. And only what is determined in the market by supply and demand, expressed in this form, is the subject of the study of probabilistic economics. In this sense it can also be called S&D economic theory, and the S&D principle itself is the main element of its basis.

1.5.2. AGENT PRINCIPLE

This is generally the most important concept, or paradigm, in respect of the markets. Here it is: every market consists of market agents, buyers and sellers, interacting quite intensively, and prone not only to competition, but also to mutually beneficial social cooperation. There are no other market forces in markets, except the forces of market agents’ interaction. All market results are a consequence of the market agents’ actions, even if their actions were strongly influenced by other factors: the state, institutions, etc. Everything that happens in markets is done by interacting market agents and therefore only agent-based models (agent action-based models or below simply action-based models) can provide a reasonable and reliable quantitative basis for any modern economic theory. And the actions of market agents in the market are exactly the issuing of bids or quotations to buy or sell, which was discussed above.

1.5.3. INSTITUTIONAL AND ENVIRONMENTAL PRINCIPLE

Markets are never completely closed or free. All market agents are constantly influenced not only by other agents, but also by numerous external forces and factors. These external forces and factors, playing the role of boundary conditions, give economic systems harmony, integrity and stability. The most important of these are, of course, institutions of various kinds, such as the state, trade unions, laws, innovations, etc. Just as important might be such forces and factors of the external environment as other markets and economies, including foreign ones, as well as natural and man-made processes, etc. The influences exerted by each of these forces and factors on the structure of market prices and on market behavior can be comparable to the effect of the market agents’ interaction. Moreover, the actions of strong external institutional and environmental factors can significantly both stimulate and impede effective operation of internal market mechanisms and even partially suppress effective functioning of the market as a whole. Thus, the influence of institutional and environmental factors should be adequately taken into account in models together with interaction between market agents.

1.5.4. DYNAMIC AND EVOLUTIONARY PRINCIPLE

Modern markets are complex non-linear nonequilibrium dynamic systems, since all market agents are in constant interaction with each other and external forces, in other words, in constant motion in search of profitable connections to buy or sell goods and services. Buyers seek to buy as low as possible, and sellers want the highest possible price. Mathematically, we can describe this time-dependent dynamic and evolutionary market process as a movement in some formal economic space of market agents acting according to objective economic laws. Therefore, this movement has a somewhat deterministic character, and the market movement itself, or the evolution of the market system, in time can be approximated by equations of motion similar to the equations of motion in physics, such as the Lagrange equations in classical mechanics or Schrödinger equations in quantum mechanics.

1.5.5. TRADE VOLUME MAXIMIZATION PRINCIPLE

In relatively free markets, buyers and sellers consciously and deliberately enter into trade deals with each other, because they enter into transactions only on mutually beneficial terms. It is not necessarily the case that they will seek to maximize their profits in every deal they make, since they understand that deals can only be mutually beneficial. But they try, usually, to increase their financial benefit by entering into as many of these mutually beneficial transactions as possible. Thus, it can be argued that the market as a whole seeks to maximize the trade volume, and moreover, to do it in monetary terms, as agents naturally seek, in the end, to increase their personal profits expressed in terms of money. This principle triggers the market process and the action of the laws of supply and demand. But the role of the state should also be taken into account, since it is present in the market as a full-fledged market agent and because, due to its enormous resources, it can, figuratively speaking, play not only the part of the first violin, but also the role of the conductor in this orchestra. Consequently, market dynamics can be approximated by applying the trade volume maximization principle to the market as a whole. Due to the fact that at present we do not have a developed mathematical body to use the more general principle of least action and the corresponding Lagrange equations of motion, the trade volume maximization still remains the only tool in this theory that helps to evaluate at least short-term trends in market dynamics.

1.5.6. UNCERTAINTY AND PROBABILITY PRINCIPLE

Uncertainty and probability always accompany human action in the markets, therefore without taking them into account it is impossible to operate successfully for a sufficiently long period of time. This is caused by the very nature of human reasoning and the fundamental human inability to accurately predict the future state of markets. Moreover, according to the institutional and environmental principle, markets are constantly under the influence of various institutions and environmental factors. For these reasons, all market agent decisions and actions, and hence all market processes and phenomena, are essentially probabilistic, so they can only be adequately described by applying probabilistic mathematical methods and models. On the same grounds, demand and supply functions should also be described in terms of probability distributions.

To introduce some certainty, let us note that the first five principles, along with the axiom, constitute the basis for building a market model in which probabilistic effects are absent or not explicitly considered. We will call such a model classical because of its certain similarity to concepts of both classical economic theory and classical mechanics. Adding the sixth principle (the uncertainty and probability principle) to this base provides a basis for building a full-fledged probabilistic theory, which is naturally broader in nature and has much greater opportunities for further development. Obviously, from the methodological point of view, the classical model can be considered as a fairly good initial approximation of the probabilistic theory, which makes it possible to quantify the probabilistic effects by comparing the results of classical and probabilistic calculations. As a matter of fact, this exact possibility is the justification for building and using the classical model.