
Полная версия
Все науки. №3, 2022. Международный научный журнал
Также АФ эффект в кристллах без центра симметрии может быть применён как новый тип элементов-фотовольтаических преобразователей энергии. КПД преобразователей световой энергии в электрическую энергию на основе фотовольтаического эффекта пака низок.
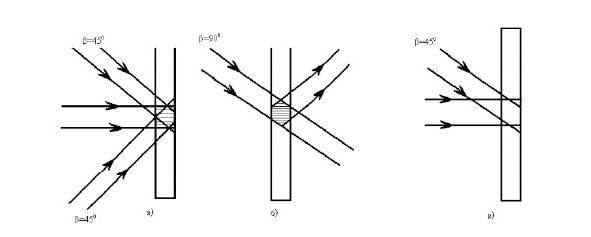
Однако, сегнето, ипеъзоэлектрики могут использоваться для генерации опорных напряжений низкой мощности. При этом спектральный чувствительность этих элементов варьируется широкой области: от вакуумной ультрафиолетовой до красной видимой области.
Имеется возможности применения этих процессов в бесеребрянной фотографии и видиконов, а также в нанотехнологии.
ЗАКЛЮЧЕНИЕ
Обнаружен и исследован фотовольтаический и фоторефрактивный эффект и определён единственное отличное от нуля фотовольтаический коэффициент
K14 =2∙10—9A∙см∙ (Вт) -1 для кубическом кристалле ZnS. Коэффициенты K14 более чем на порядок превышают соответствующие коэффициенты в LiNbO3:Fe.
Показана возможность использование фотопьезоэлектриков в голографической записи. В этом случае запись осуществляется двумя когерентными лучами с поляризацией соответствующей фотовольтаическому току. Реконстуирование записанной голограммы достигается путем освещения кристалла лучом когерентного света той же длины волны. Однако, поляризация этого луча выбирается таким образом, чтобы освещение не приводило к генерации фотовольтаического тока. Стирание записанной голограммы достигает путем равномерного освещение поверхности лучом света с предыдущей поляризации. Также стирание может осуществляться путем отжига кристалла при 170С.
Автор благодарит С. Шамирзаеву за обсуждение.
Использованная литература
1. Рывкин. С. М. Фотоэлектрические явления в полупроводниках. М.: Физматгиз. 1963. 494С.
2. Бьюб Р. Фотопроводимость твердых тел. М.: ИЛ. 1962. 558С.
3. Э.И.Адирович. Фотоэлектрические явления в полупроводниках и оптоэлектроника. Ташкент: Фан. 1972. 343 С.
4. Glass A.M., Voh der Linbe D., Nerren T.J.//High- voltage Bulk Photovoltaic effect and the Photorefractive process in LiNbO3. J. Appl. Phys. Let, 1974. N4. v.25. p.233—236.
5. Фридкин В. М. Фотосегнетоэлектрики. М.: Наука. 1979. С.186—216.
6. В.И.Белиничер. Исследования фотогальванических эффектов в кристаллах. Дисс. на соискание. докт. физ-мат. наук. Новосибирск. 1982. 350 С.
7. Леванок А. П., Осипов В. В. Механизмы фоторефрактивного эффекта.// Изв. Ан. Россия, 1977. Т.41. №4. C.752—769.
8. Стурман Б. И., Фридкин В. М. Фотогальванические эффекты в средах без центра инверсии. М.: Наука. 1992. 208 С.
9. Фридкин В. М. //Объемный фотовольтаический эффект в кристаллах без центра симметрии. Кристаллография. 2001. Т.46 №4. С.722—726.
АЛЮМИНИЕВАЯ РЕЗОНАНСНАЯ ЯДЕРНАЯ РЕАКЦИЯ
Алиев Ибратжон Хатамович
Студент 2 курса факультета математики-информатики Ферганского Госудрственного Университета
Ферганский Государственный Университет, Узбекистан
Аннотация. Развитие физики резонансных ядерных реакций, о которой неоднократно говорилось в целом ряде самых различных публикаций, становиться причиной для дальнейшего исследования применения данного метода относительно различных ядер и проведения подробных расчётов.
Ключевые слова: ядерная реакция, протон, изотоп магния, кулоновский барьер, длина волны, частицы, истинное сечение.
Annotation. The development of the physics of resonant nuclear reactions, which has been repeatedly discussed in a number of very different publications, becomes a reason for further investigation of the application of this method with respect to various nuclei and for conducting detailed calculations.
Keywords: nuclear reaction, proton, magnesium isotope, Coulomb barrier, wavelength, particles, true cross section.
Пятая ядерная реакция, исследуемая на сегодняшний день, что и придаёт ей данный коэффициент, представляется следующим образом (1).
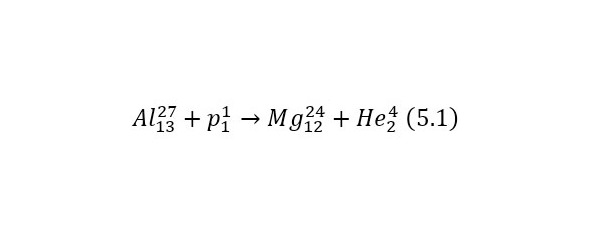
Протон с энергией в 4,457595117 МэВ и массой в 1,00728 а. е. м., налетает на алюминий-27 с атомной массой в 26,98153863 а. е. м., с выделением изотопа магния-24 с массой 23,9850417 а. е. м., а также альфа-частицы с массой 4,001506179 а. е. м.
Изначально, необходимо определить, какое количество энергии затратит протон, приближаясь к ядру алюминия, а именно высоту кулоновского барьера (3), определив радиус ядра алюминия-27 в (2).
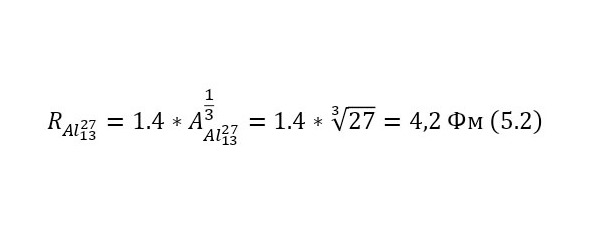
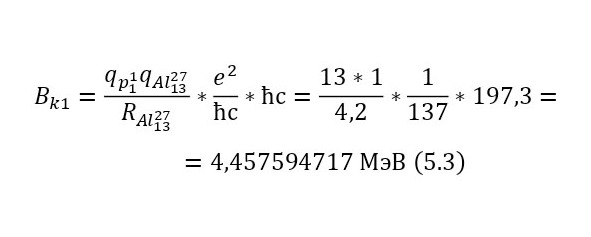
Следовательно, нынешняя энергия протона, после затраты на кулоновский барьер, составляет 0,4 эВ. Теперь, необходимо вычислить энергетический выход данной ядерной реакции, с указанными массами в (4).
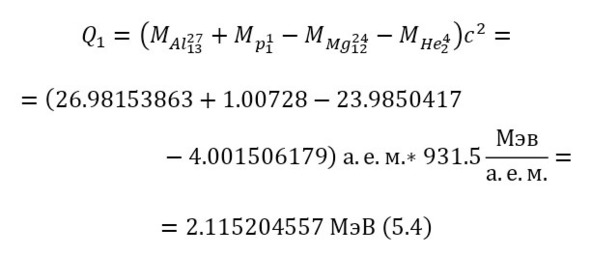
Поскольку эта реакция экзо-энергетическая, то нет смысла вычислять для неё порог реакции, остаётся лишь записать пару энергетических уравнений (5—6) и затем вычислить энергии, приобретаемые магнием-24 и альфа-частицей.
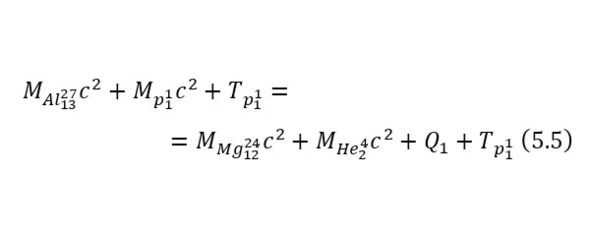
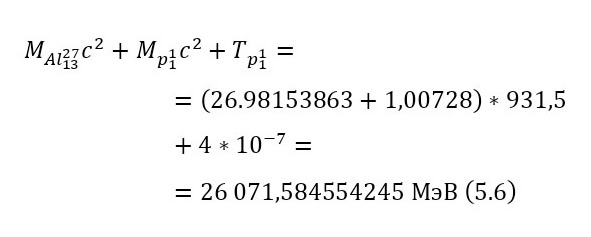
Из этих энергетических уравнений стало ясно, что кроме выхода реакции, добавляется и оставшаяся кинетическая энергия, благодаря чему общая энергия, распределяемая между частицами, составляет 2,115204957 МэВ из равенства (7). Теперь, для распределения этих энергий достаточно воспользоваться (8) и (9).
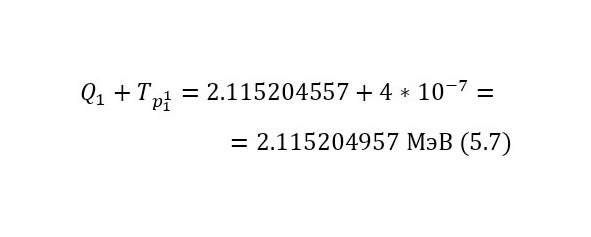
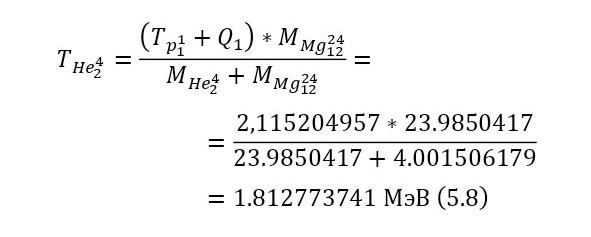
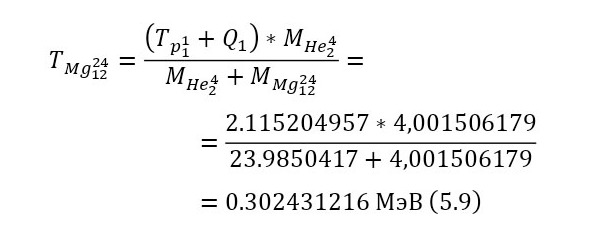
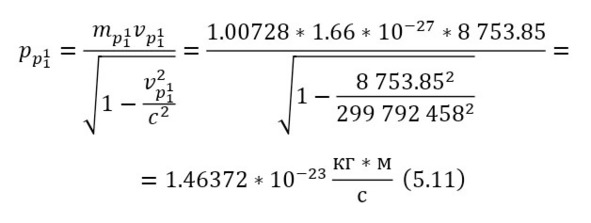
И наконец, остаётся определить сечение ядерной реакции и число взаимодействий. Изначально, необходимо вычислить длину волны налетающих протонов, для этого достаточно определить их импульс через (11), перед этим вычислив скорость в (10), а затем уже длину волны в (12).
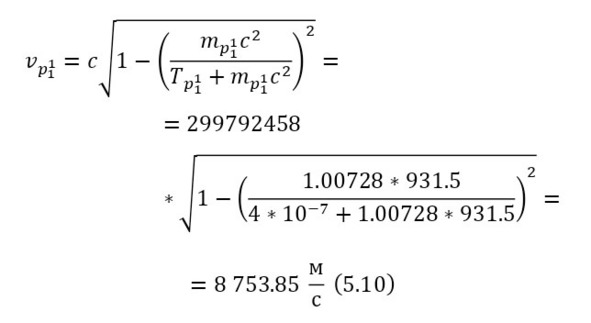
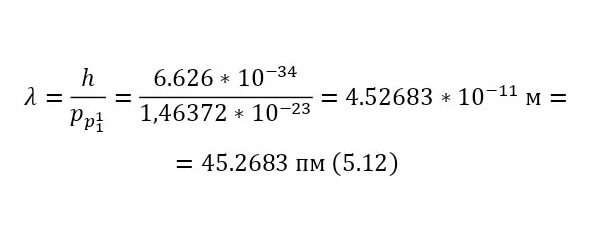
Переходя уже к исчислению сечений, достаточно воспользоваться (13), но также необходимо использование коэффициента, о котором говорилось ранее, по этой причине применяется и (14), и только после вычисляется истинное сечение (15), для некоторых подсчётов, этот коэффициент становится равным единице, поэтому просто не указывается, но в данном случае, если подсчитать таким же образом.
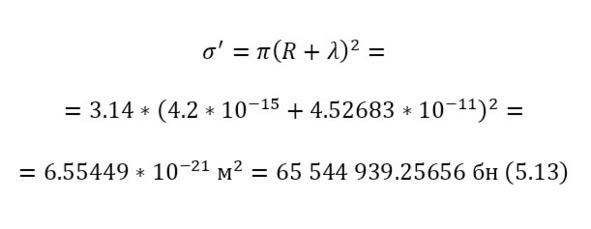
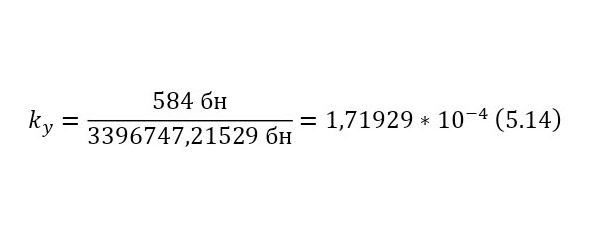
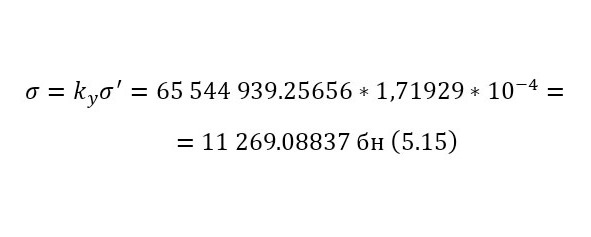
Теперь, когда сечение известно, для этой реакции, остаётся ввести число взаимодействий (19), перед этим вычислим число атомов на кубометр (16) и указав толщину пластины в 78 мкм, поскольку пробег протона (максимальное расстояние на котором может пройти при определённой энергии) с энергией 3 МэВ составляет это значение.
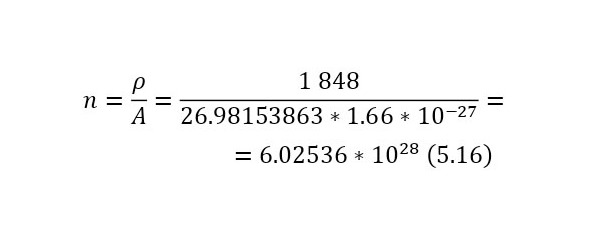
А также необходимо определить в (18) начальное число бомбардирующих протонов, указав, что их общая сила тока 25 А, а время одного акта, который вытекает уже из параметров циклотрона, описываемый в предыдущих главах составляет 328,13 нс, что гораздо больше времени даже самой долгой реакции, откуда можно вычислить заряд (17), а из него уже и число протонов (18).
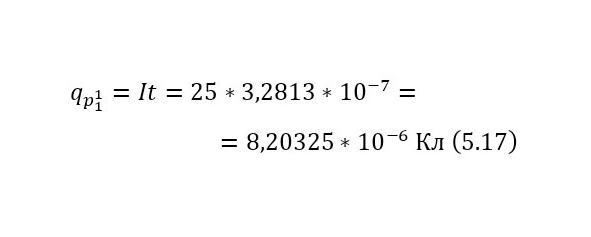
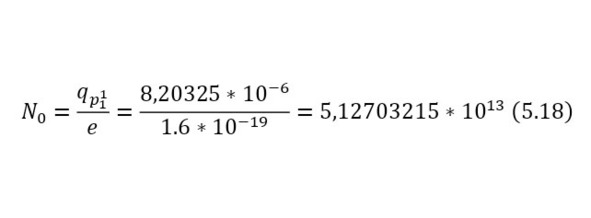
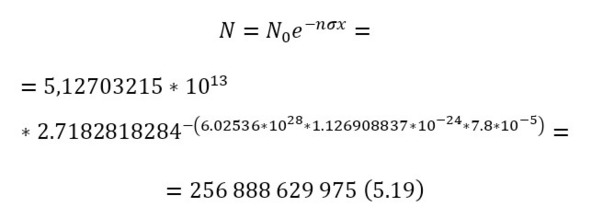
Это число всех частиц, прошедших сквозь пластину и не вошедших в реакцию, а для того, чтобы вычислить те, которые вошли в реакцию, достаточно определить разность в (20), а затем уже вычислить из них заряд, учитывая, что альфа-частица несёт 2 элементарных заряда (21) и силу тока (22).
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.


