On the various forces of nature and their relations to each other

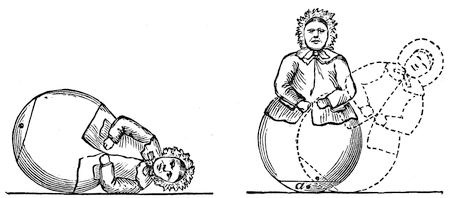
Fig. 5. and Fig. 6.

Here is a toy I happened to see the other day, which will, I think, serve to illustrate our subject very well. That toy ought to lie something in this manner (fig. 5); and would do so if it were uniform in substance. But you see it does not; it will get up again. And now philosophy comes to our aid; and I am perfectly sure, without looking inside the figure, that there is some arrangement by which the centre of gravity is at the lowest point when the image is standing upright; and we may be certain, when I am tilting it over (see fig. 6), that I am lifting up the centre of gravity (a), and raising it from the earth. All this is effected by putting a piece of lead inside the lower part of the image, and making the base of large curvature; and there you have the whole secret. But what will happen if I try to make the figure stand upon a sharp point? You observe, I must get that point exactly under the centre of gravity, or it will fall over thus [endeavouring unsuccessfully to balance it]; and this you see is a difficult matter – I cannot make it stand steadily. But if I embarrass this poor old lady with a world of trouble, and hang this wire with bullets at each end about her neck, it is very evident that, owing to there being those balls of lead hanging down on either side, in addition to the lead inside, I have lowered the centre of gravity, and now she will stand upon this point (fig. 7); and what is more, she proves the truth of our philosophy by standing sideways.

Fig. 7.

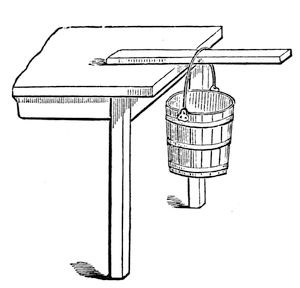
Fig. 8.

I remember an experiment which puzzled me very much when a boy. I read it in a conjuring book, and this was how the problem was put to us: “How,” as the book said, “how to hang a pail of water, by means of a stick, upon the side of a table” (fig. 8). Now, I have here a table, a piece of stick, and a pail, and the proposition is, how can that pail be hung to the edge of this table? It is to be done; and can you at all anticipate what arrangement I shall make to enable me to succeed? Why, this. I take a stick, and put it in the pail between the bottom and the horizontal piece of wood, and thus give it a stiff handle – and there it is; and what is more, the more water I put into the pail the better it will hang. It is very true that before I quite succeeded I had the misfortune to push the bottoms of several pails out; but here it is hanging firmly (fig. 9), and you now see how you can hang up the pail in the way which the conjuring books require.

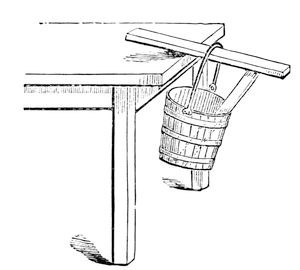
Fig. 9.

Again, if you are really so inclined (and I do hope all of you are), you will find a great deal of philosophy in this [holding up a cork and a pointed thin stick about a foot long]. Do not refer to your toy-books, and say you have seen that before. Answer me rather, if I ask you have you understood it before? It is an experiment which appeared very wonderful to me when I was a boy; I used to take a piece of cork (and I remember, I thought at first that it was very important that it should be cut out in the shape of a man; but by degrees I got rid of that idea), and the problem was to balance it on the point of a stick. Now, you will see I have only to place two sharp-pointed sticks one on each side, and give it wings, thus, and you will find this beautiful condition fulfilled.

Fig. 10.

We come now to another point: – All bodies, whether heavy or light, fall to the earth by this force which we call gravity. By observation, moreover, we see that bodies do not occupy the same time in falling. I think you will be able to see that this piece of paper and that ivory ball fall with different velocities to the table [dropping them]; and if, again, I take a feather and an ivory ball, and let them fall, you see they reach the table or earth at different times – that is to say, the ball falls faster than the feather. Now, that should not be so, for all bodies do fall equally fast to the earth. There are one or two beautiful points included in that statement. First of all, it is manifest that an ounce, or a pound, or a ton, or a thousand tons, all fall equally fast, no one faster than another: here are two balls of lead, a very light one and a very heavy one, and you perceive they both fall to the earth in the same time. Now, if I were to put into a little bag a number of these balls sufficient to make up a bulk equal to the large one, they would also fall in the same time; for if an avalanche fall from the mountains, the rocks, snow and ice, together falling towards the earth, fall with the same velocity, whatever be their size.

I cannot take a better illustration of this than that of gold leaf, because it brings before us the reason of this apparent difference in the time of the fall. Here is a piece of gold-leaf. Now, if I take a lump of gold and this gold-leaf, and let them fall through the air together, you see that the lump of gold – the sovereign, or coin – will fall much faster than the gold leaf. But why? They are both gold, whether sovereign or gold-leaf. Why should they not fall to the earth with the same quickness? They would do so, but that the air around our globe interferes very much where we have the piece of gold so extended and enlarged as to offer much obstruction on falling through it. I will, however, shew you that gold-leaf does fall as fast when the resistance of the air is excluded – for if I take a piece of gold-leaf and hang it in the centre of a bottle, so that the gold, and the bottle, and the air within shall all have an equal chance of falling, then the gold-leaf will fall as fast as anything else. And if I suspend the bottle containing the gold-leaf to a string, and set it oscillating like a pendulum, I may make it vibrate as hard as I please, and the gold-leaf will not be disturbed, but will swing as steadily as a piece of iron would do; and I might even swing it round my head with any degree of force, and it would remain undisturbed. Or I can try another kind of experiment: – if I raise the gold-leaf in this way [pulling the bottle up to the ceiling of the theatre by means of a cord and pulley, and then suddenly letting it fall to within a few inches of the lecture-table], and allow it then to fall from the ceiling downwards (I will put something beneath to catch it, supposing I should be maladroit), you will perceive that the gold-leaf is not in the least disturbed. The resistance of the air having been avoided, the glass bottle and gold-leaf all fall exactly in the same time.

Here is another illustration, – I have hung a piece of gold-leaf in the upper part of this long glass vessel, and I have the means, by a little arrangement at the top, of letting the gold-leaf loose. Before we let it loose we will remove the air by means of an air pump, and while that is being done, let me shew you another experiment of the same kind. Take a penny-piece, or a half-crown, and a round piece of paper a trifle smaller in diameter than the coin, and try them, side by side, to see whether they fall at the same time [dropping them]. You see they do not – the penny-piece goes down first. But, now place this paper flat on the top of the coin, so that it shall not meet with any resistance from the air, and upon then dropping them you see they do both fall in the same time [exhibiting the effect]. I dare say, if I were to put this piece of gold-leaf, instead of the paper, on the coin, it would do as well. It is very difficult to lay the gold-leaf so flat that the air shall not get under it and lift it up in falling, and I am rather doubtful as to the success of this, because the gold-leaf is puckery; but will risk the experiment. There they go together! [letting them fall] and you see at once that they both reach the table at the same moment.

We have now pumped the air out of the vessel, and you will perceive that the gold-leaf will fall as quickly in this vacuum as the coin does in the air. I am now going to let it loose, and you must watch to see how rapidly it falls. There! [letting the gold loose] there it is, falling as gold should fall.

I am sorry to see our time for parting is drawing so near. As we proceed, I intend to write upon the board behind me certain words, so as to recall to your minds what we have already examined – and I put the word Forces as a heading; and I will then add, beneath, the names of the special forces according to the order in which we consider them: and although I fear that I have not sufficiently pointed out to you the more important circumstances connected with this force of Gravitation, especially the law which governs its attraction (for which, I think, I must take up a little time at our next meeting), still I will put that word on the board, and hope you will now remember that we have in some degree considered the force of gravitation– that force which causes all bodies to attract each other when they are at sensible distances apart, and tends to draw them together.

LECTURE II.

GRAVITATION – COHESION

Do me the favour to pay me as much attention as you did at our last meeting, and I shall not repent of that which I have proposed to undertake. It will be impossible for us to consider the Laws of Nature, and what they effect, unless we now and then give our sole attention, so as to obtain a clear idea upon the subject. Give me now that attention, and then, I trust, we shall not part without your knowing something about those Laws, and the manner in which they act. You recollect, upon the last occasion, I explained that all bodies attracted each other, and that this power we called gravitation. I told you that when we brought these two bodies [two equal sized ivory balls suspended by threads] near together, they attracted each other, and that we might suppose that the whole power of this attraction was exerted between their respective centres of gravity; and furthermore, you learned from me, that if, instead of a small ball, I took a larger one, like that [changing one of the balls for a much larger one], there was much more of this attraction exerted; or, if I made this ball larger and larger, until, if it were possible, it became as large as the Earth itself – or, I might take the Earth itself as the large ball – that then the attraction would become so powerful as to cause them to rush together in this manner [dropping the ivory ball]. You sit there upright, and I stand upright here, because we keep our centres of gravity properly balanced with respect to the earth; and I need not tell you that on the other side of this world the people are standing and moving about with their feet towards our feet, in a reversed position as compared with us, and all by means of this power of gravitation to the centre of the earth.

I must not, however, leave the subject of gravitation, without telling you something about its laws and regularity; and first, as regards its power with respect to the distance that bodies are apart. If I take one of these balls and place it within an inch of the other, they attract each other with a certain power. If I hold it at a greater distance off, they attract with less power; and if I hold it at a greater distance still, their attraction is still less. Now this fact is of the greatest consequence; for, knowing this law, philosophers have discovered most wonderful things. You know that there is a planet, Uranus, revolving round the sun with us, but eighteen hundred millions of miles off; and because there is another planet as far off as three thousand millions of miles, this law of attraction, or gravitation, still holds good – and philosophers actually discovered this latter planet, Neptune, by reason of the effects of its attraction at this overwhelming distance. Now I want you clearly to understand what this law is. They say (and they are right) that two bodies attract each other inversely as the square of the distance– a sad jumble of words until you understand them; but I think we shall soon comprehend what this law is, and what is the meaning of the “inverse square of the distance.”

Fig. 11.

I have here (fig. 11) a lamp A, shining most intensely upon this disc, B, C, D; and this light acts as a sun by which I can get a shadow from this little screen, B F (merely a square piece of card), which, as you know, when I place it close to the large screen, just shadows as much of it as is exactly equal to its own size. But now let me take this card E, which is equal to the other one in size, and place it midway between the lamp and the screen: now look at the size of the shadow B D – it is four times the original size. Here, then, comes the “inverse square of the distance.” This distance, A E, is one, and that distance, A B, is two; but that size E being one, this size B D of shadow is four instead of two, which is the square of the distance; and, if I put the screen at one-third of the distance from the lamp, the shadow on the large screen would be nine times the size. Again, if I hold this screen here, at B F, a certain amount of light falls on it; and if I hold it nearer the lamp at E, more light shines upon it. And you see at once how much – exactly the quantity which I have shut off from the part of this screen, B D, now in shadow; moreover, you see that if I put a single screen here, at G, by the side of the shadow, it can only receive one-fourth of the proportion of light which is obstructed. That, then, is what is meant by the inverse of the square of the distance. This screen E is the brightest, because it is the nearest; and there is the whole secret of this curious expression, inversely as the square of the distance. Now, if you cannot perfectly recollect this when you go home, get a candle and throw a shadow of something – your profile, if you like – on the wall, and then recede or advance, and you will find that your shadow is exactly in proportion to the square of the distance you are off the wall; and then if you consider how much light shines on you at one distance, and how much at another, you get the inverse accordingly. So it is as regards the attraction of these two balls – they attract according to the square of the distance, inversely. I want you to try and remember these words, and then you will be able to go into all the calculations of astronomers as to the planets and other bodies, and tell why they move so fast, and why they go round the sun without falling into it, and be prepared to enter upon many other interesting inquiries of the like nature.

Let us now leave this subject which I have written upon the board under the word Force – Gravitation – and go a step further. All bodies attract each other at sensible distances. I shewed you the electric attraction on the last occasion (though I did not call it so); that attracts at a distance: and in order to make our progress a little more gradual, suppose I take a few iron particles [dropping some small fragments of iron on the table]. There, I have already told you that in all cases where bodies fall, it is the particles that are attracted. You may consider these then as separate particles magnified, so as to be evident to your sight; they are loose from each other – they all gravitate – they all fall to the earth – for the force of gravitation never fails. Now, I have here a centre of power which I will not name at present, and when these particles are placed upon it, see what an attraction they have for each other.

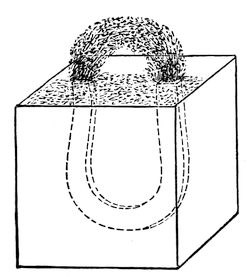
Fig. 12.

Here I have an arch of iron filings (fig. 12) regularly built up like an iron bridge, because I have put them within a sphere of action which will cause them to attract each other. See! – I could let a mouse run through it, and yet if I try to do the same thing with them here [on the table], they do not attract each other at all. It is that [the magnet] which makes them hold together. Now, just as these iron particles hold together in the form of an elliptical bridge, so do the different particles of iron which constitute this nail hold together and make it one. And here is a bar of iron – why, it is only because the different parts of this iron are so wrought as to keep close together by the attraction between the particles that it is held together in one mass. It is kept together, in fact, merely by the attraction of one particle to another, and that is the point I want now to illustrate. If I take a piece of flint and strike it with a hammer, and break it thus [breaking off a piece of the flint], I have done nothing more than separate the particles which compose these two pieces so far apart, that their attraction is too weak to cause them to hold together, and it is only for that reason that there are now two pieces in the place of one. I will shew you an experiment to prove that this attraction does still exist in those particles, for here is a piece of glass (for what was true of the flint and the bar of iron is true of the piece of glass, and is true of every other solid – they are all held together in the lump by the attraction between their parts), and I can shew you the attraction between its separate particles; for if I take these portions of glass, which I have reduced to very fine powder, you see that I can actually build them up into a solid wall by pressure between two flat surfaces. The power which I thus have of building up this wall is due to the attraction of the particles, forming as it were the cement which holds them together; and so in this case, where I have taken no very great pains to bring the particles together, you see perhaps a couple of ounces of finely-pounded glass standing as an upright wall. Is not this attraction most wonderful? That bar of iron one inch square has such power of attraction in its particles – giving to it such strength – that it will hold up twenty tons weight before the little set of particles in the small space, equal to one division across which it can be pulled apart, will separate. In this manner suspension bridges and chains are held together by the attraction of their particles; and I am going to make an experiment which will shew how strong is this attraction of the particles. [The Lecturer here placed his foot on a loop of wire fastened to a support above, and swung with his whole weight resting upon it for some moments.] You see while hanging here all my weight is supported by these little particles of the wire, just as in pantomimes they sometimes suspend gentlemen and damsels.

How can we make this attraction of the particles a little more simple? There are many things which if brought together properly will shew this attraction. Here is a boy’s experiment (and I like a boy’s experiment). Get a tobacco-pipe, fill it with lead, melt it, and then pour it out upon a stone, and thus get a clean piece of lead (this is a better plan than scraping it – scraping alters the condition of the surface of the lead). I have here some pieces of lead which I melted this morning for the sake of making them clean. Now these pieces of lead hang together by the attraction of their particles; and if I press these two separate pieces close together, so as to bring their particles within the sphere of attraction, you will see how soon they become one. I have merely to give them a good squeeze, and draw the upper piece slightly round at the same time, and here they are as one, and all the bending and twisting I can give them will not separate them again: I have joined the lead together, not with solder, but simply by means of the attraction of the particles.

This, however, is not the best way of bringing those particles together – we have many better plans than that; and I will shew you one that will do very well for juvenile experiments. There is some alum crystallised very beautifully by nature (for all things are far more beautiful in their natural than their artificial form), and here I have some of the same alum broken into fine powder. In it I have destroyed that force of which I have placed the name on this board – Cohesion, or the attraction exerted between the particles of bodies to hold them together. Now I am going to shew you that if we take this powdered alum and some hot water, and mix them together, I shall dissolve the alum – all the particles will be separated by the water far more completely than they are here in the powder; but then, being in the water, they will have the opportunity as it cools (for that is the condition which favours their coalescence) of uniting together again and forming one mass.7

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

1

Page 13. The opening lecture was twice postponed on account of Dr. Faraday’s illness.

2

Page 22. Platinum, with one exception, the heaviest body known, is 21½ times heavier than water.

3

Page 22. Aluminium is 2½ times heavier than water.

4

Pages 23 and 24. Power or Property in Water.– This power – the heat by which the water is kept in a fluid state – is said, under ordinary circumstances, to be latent or insensible. When, however, the water changes its form, and, by uniting with the lime or sulphate of copper, becomes solid, the heat which retained it in a liquid state is evolved.

5

Page 23. Anhydrous Sulphate of Copper: sulphate of copper deprived of its water of crystallisation. To obtain it, the blue sulphate is calcined in an earthen crucible.

6

Page 29. Add a little liquid to the marble, and decompose it.– Marble is composed of carbonic acid and lime, and, in chemical language, is called carbonate of lime. When sulphuric acid is added to it, the carbonic acid is set free, and the sulphuric acid unites with the lime to form sulphate of lime.

Carbonic acid, under ordinary circumstances, is a colourless invisible gas, about half as heavy again as air. Dr. Faraday first shewed that, under great pressure, it could be obtained in a liquid state. Thilorier, a French chemist, afterwards found that it could be solidified.

7

Page 55. Crystallisation of Alum.– The solution must be saturated – that is, it must contain as much alum as can possibly be dissolved. In making the solution, it is best to add powdered alum to hot water as long as it dissolves; and when no more is taken up, allow the solution to stand a few minutes, and then pour it off from the dirt and undissolved alum.