Вероятностная теория фондовых бирж

Утверждение 2. Вероятностная экономика – это не просто одна из многих моделей конкретных экономических систем, а достаточно универсальный метод численного описания и исследования любых рыночных экономических систем как локальных, так и глобальных. После изучения их этим методом и выявления основных эффектов, процессов и закономерностей в их функционировании можно уже строить различные простые модели этих систем. Тем не менее, во избежание недоразумений, стоит отметить, что вероятностная экономика – далеко не есть «теория всего». Она нацелена на исследование, может быть, самого важного, но далеко не всех важных злободневных вопросов экономической теории, а именно: каким образом из отдельных действий рыночных агентов, т.е. предъявления ими своих индивидуальных спросов и предложений, вытекают структура и особенности поведения рынка в целом. Поэтому еще раз подчеркнем, что все, что описано в данной монографии, и все, что утверждается в ней, касается только прямой задачи экономики, если не оговорено особо.

Утверждение 3. Предложенный математический аппарат для описания динамики рынков построен на использовании заявок или котировок рыночных агентов, поэтому он автоматически учитывает все принципы теории, поскольку при выборе котировок рыночные агенты в каждый момент времени учитывают всю поступающую на рынок информацию. Другими словами, они находятся под постоянным воздействием всех сил и влияний, действующих на рынке в данный момент времени: это и влияние других агентов, активов и рынков; это и действие институциональных и средовых факторов и т.д., что находит отражение в регулярном изменении ими своих котировок.

В последующих двух разделах мы детально опишем математический аппарат вероятностной экономики, построенной на базе действий агентов, и проиллюстрируем его работу на примере простейшего модельного рынка с одним покупателем, одним продавцом и одним торгуемым товаром. Будет показано, что наиболее яркие особенности и закономерности в поведении рынков проявляются уже в такой простейшей двухагентной модели. Расширение этой теории для многоагентных рынков с одним торгуемым товаром будет представлено в последующих главах.

1.6. КЛАССИЧЕСКАЯ ТЕОРИЯ ДВУХАГЕНТНОГО РЫНКА

Заметим, что поскольку в классической теории, или классике, мы пренебрегаем всеми вероятностными эффектами, то принцип неопределенности и вероятности в классике мы не рассматриваем, хотя понятно, что он играет важную роль в вероятностной теории. Вряд ли стоит серьезно обсуждать, какая из этих двух теорий лучше. Как и в случае классической и квантовой механики, предпочтительнее говорить о разных областях применения классической (в определенном смысле детерминистской) и вероятностной теорий, что будет не раз продемонстрировано нами далее. Напомним, что под классической теорией в данной книге понимается просто начальное приближение теории вероятностной, в котором в явном виде не учитывается принцип неопределенности и вероятности.

Итак, мы подробно опишем такой подход к изучению динамики, или эволюции, экономики в рамках классики на примере простейшей модели, а именно, рынка с одним покупателем и одним продавцом, торгующим одним товаром, например зерном. Экономическое пространство в этом случае является, очевидно, двумерным.

1.6.1. ДИСКРЕТНАЯ СТРАТЕГИЯ РЫНОЧНЫХ АГЕНТОВ

Рассмотрим типичную ситуацию на рынке, в котором есть реальные потенциальные покупатель и продавец определенного товара, скажем зерна. Покупатель хочет купить товар в количестве qD по цене pD, а продавец хочет продать товар в количестве qS по цене pS. Эти четыре параметра полностью характеризуют состояние рынка в классике в каждый момент времени. Это обычное дело на рынке, что и цены, и количества покупателя и продавца не равны друг другу. Поэтому, если они оба будут настаивать на своих предложениях, то сделки, очевидно, не будет. Самый старый, хорошо отлаженный за многие годы с момента возникновения рынков механизм разрешения таких торговых споров заключается в том, что покупатель и продавец вступают в торговые переговоры с целью достижения ими согласия на сделку купли-продажи на условиях, которые устраивают обе стороны. Опишем этот процесс переговоров на математическом языке следующим образом. Пусть функции pD(t) и qD(t) обозначают цену и количество товара, желаемые и предлагаемые покупателем во время переговоров с продавцом о купле-продаже в определенный момент времени t. Аналогично пусть функции pS(t) и qS(t) будут обозначать цену и количество товара, желаемые и предлагаемые продавцом во время переговоров с покупателем на рынке. По своему смыслу введенные выше значения цен и количеств есть основное содержание агентных заявок на покупку или продажу товара. Ниже, для краткости, будем называть эти желаемые и предлагаемые значения цен и количеств котировками покупателя и продавца. А такую линию поведения агентов на рынке будем называть дискретной или точечной стратегией, поскольку в каждый момент времени t эти котировки представляются одной точкой в двумерном пространстве, например, точкой А с координатами pD(t) и qD(t) для покупателя и точкой В с координатами pS(t) и qS(t) для продавца, как это представлено на рис. 1.2. Эти котировки выставляются, конечно, с учетом всех обстоятельств, влияющих на работу рынка: институтов и т.п. На наш взгляд, выставление этих котировок рыночными агентами суть главного рыночного феномена классической экономической теории в представлении австрийской экономической школы, а именно рыночного процесса [Мизес, 2005], состоящего из конкретных актов выбора и действий рыночных агентов, которые в конечном итоге приводят покупателей и продавцов к заключению сделок купли-продажи. Графически, мы можем изобразить эти котировки как траектории движения агентов в экономическом пространстве (рис. 1.3). В реальной рыночной жизни эти котировки являются дискретными функциями времени, но, для простоты, мы будем изображать их графически (так же, как и функции S&D) как непрерывные прямые линии. Такое приближение не приводит в данном случае к потере общности, поскольку эти функции призваны только проиллюстрировать самые общие детали механизма работы рынка и способ их описания (см. рис. 1.3). По экономическому смыслу такие диаграммы характеризуют временную динамику рынка.

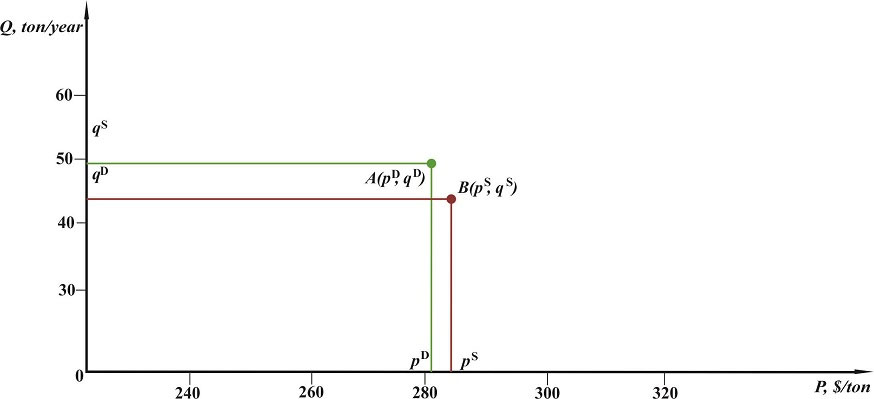
Рис. 1.2. Графическое представление точечной стратегии рыночного поведения покупателя A(pD, qD) и продавца B(pS, qS) точками в двумерном пространстве цены-количества в некоторый определенный момент времени для модельного рынка зерна. pD = 280,0 $/ton, qD = 50,0 ton/year, pS = 285,0 $/ton, qS = 52,0 ton/year.

Мы будем говорить (для краткости) об этом совокупном движении агентов как о поведении рынка, а иногда – как об эволюции экономики во времени. Все эти термины являются, по сути, синонимами в данном контексте обсуждения. Таким образом, выставляя желаемые цены и количества в качестве своих котировок, покупатели и продавцы принимают участие в рыночном процессе, протекающем здесь в формате переговоров между торгующимися людьми (homo negotians), стремящимися выторговать для себя наилучшие условия при заключении сделки и достичь рыночных целей. Заметим, что в действительности в состав действий рыночных агентов наряду с выставлением котировок входят также процедуры заключения итоговых сделок, но последние учитываются в таком подходе автоматически путем изменения заявок рыночными агентами после заключения сделок. Поэтому нет необходимости явным образом включать в состав действий агентов процедуру заключения сделок, достаточно принимать во внимание только процесс выставления ими котировок в течение торгов.

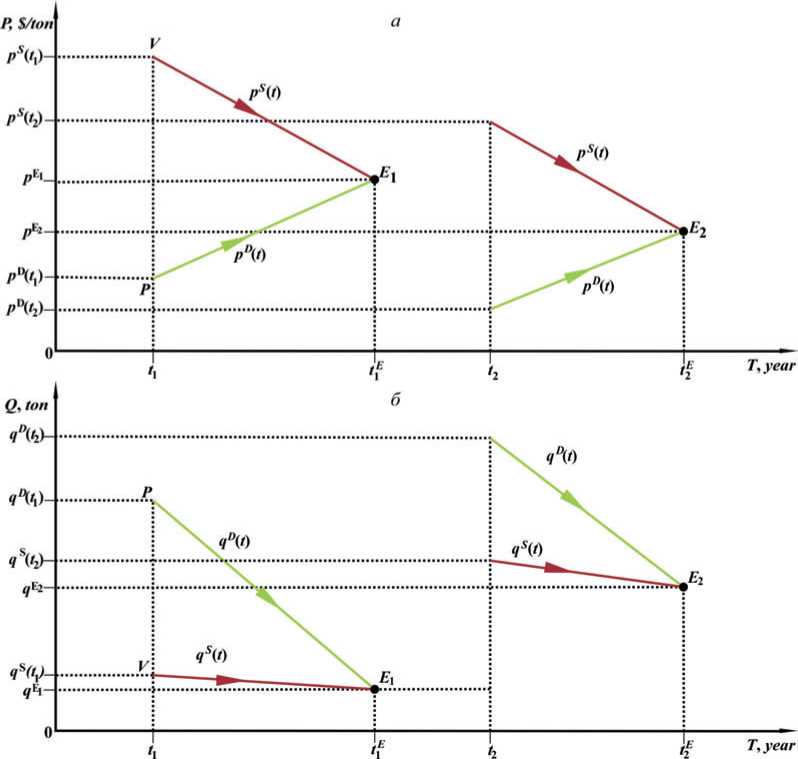
Рис. 1.3. Диаграмма траекторий движения покупателя и продавца. Изображена динамика классической двухагентной рыночной экономики в экономическом пространстве цены (а) и количества (б). В совокупности обе части рисунка представляют эволюцию экономики во времени в двумерном PQ-пространстве.

Можно весь этот торговый процесс, или просто торг, трактовать как динамическую деловую игру между покупателем и продавцом с целью извлечения прибыли или достижения некой другой цели.

1.6.2. КОНЦЕПЦИЯ ЭКОНОМИЧЕСКОГО РАВНОВЕСИЯ В КЛАССИКЕ

Предположим, что переговоры прошли удачно и завершились заключением сделки купли-продажи в момент времени t1E. Это означает, что в этот момент времени значения ценовых (pD(t) и pS(t)), а также количественных (qD(t) и qS(t)) котировок, становятся равными, так как очевидно, что в контракте могут быть указаны только конкретные взаимно-согласованные цена p1E и количество q1E товара. Будем полагать, что в этой переговорной модели есть определенный смысл называть данные значения цены и количества рыночными ценой и количеством товара и считать, что сам рынок при этих значениях цены и количества товара приходит в равновесие или достигает своего равновесного состояния. Формально это описывается с помощью следующих равенств для рыночных цены и количества:

Итак, для двухагентной модели мы получили такой тривиальный, но многозначительный результат: сам факт достижения равновесия дает возможность осуществить сделку и максимизировать объем торгов в денежном выражении. Этот вывод в данном простом случае вполне очевиден: нет согласия, нет равновесия, нет сделки, объем торгов нулевой. Но мы покажем далее, что этот вывод имеет достаточно универсальный характер, что согласуется с постулированным принципом максимизации объема торгов. Кстати, легко показать, что в рамках неоклассической теории в точке равновесия достигается максимум объема торгов в натуральном выражении, т.е. достигается максимум количества проданного товара.

Далее, поскольку жизнь не стоит на месте, покупатель и продавец могут еще не раз встречаться и заключать новые сделки, но уже в новых условиях и, очевидно, с другими ценами и количествами, то для удобства мы будем называть p1E первой рыночной ценой, а q1E – первым рыночным количеством. Таким образом, в момент времени t1 интересы покупателя и продавца в первый раз совпали, они были оптимальным образом удовлетворены путем заключения сделки купли-продажи. При этом агенты, естественно, в ходе рыночного процесса (переговоров и изменения котировок) неявным образом принимали во внимание влияние внешней окружающей среды и институциональных факторов на этом и других рынках, т.е. экономики в целом. Здесь можно заметить схожесть в движении экономической системы в экономическом пространстве, описываемом с помощью траекторий покупателя pD(t) и qD(t) и продавца pS(t) и qS(t), и в движении двухчастичной физической системы в реальном пространстве, описываемом траекториями частиц х1(t) и х2(t), которые, кстати, также являются результатом действия определенного физического принципа максимизации, а именно принципа наименьшего действия на физическую систему.

Отмеченная аналогия с физической системой наводит на мысль использовать аналогичный математический аппарат, аналитический и графический. На рис. 1.3, для начала, мы даем графическое представление этих траекторий движения агентов в зависимости от времени с помощью подходящих систем координат время – цена (T, P) и время – количество (T, Q), аналогично тому, как происходит построение траекторий частиц в классической механике. Заметим, что рис. 1.3 отражает определенную стандартную ситуацию на рынке, когда покупатель и продавец намеренно встречаются в момент времени t1 и начинают обсуждать потенциальную сделку путем взаимного обмена информацией об их условиях, прежде всего желаемых цен и количества товара. Во время переговоров они непрерывно изменяют свои котировки до тех пор, пока не соглашаются на окончательные условия по цене p1E и количеству q1E в момент времени t1E. Такая простейшая «переговорная» рыночная модель применима, например, для экономики вымышленного острова, на котором, скажем для определенности, раз в году путем переговоров происходит торговля зерном между фермером и охотником. Для определенности, будем считать, что они используют для расчетов американский доллар, $. Для наглядности, на рис. 1.3, как и на последующих рисунках, мы используем стрелки для отражения направления движения агентов во время рыночного процесса.

Итак, в нашей переговорной классической модели вплоть до момента t1 рынок находится в простейшем состоянии покоя, здесь нет торговли вообще. В момент времени t1  на рынке появляются покупатель и продавец зерна, которые устанавливают свои начальные желаемые цены и количество зерна: pD(t1), pS(t1) и qD(t1), qS(t1). Точки P и V на графике показывают положение покупателя и продавца в начальный момент времени t1, когда начинаются торговые переговоры. Естественно, желания покупателя и продавца сразу не совпадают, покупатель хочет низкую цену, но продавец борется за более высокую цену. Однако оба нуждаются в достижении понимания и последующего заключения сделки, в противном случае фермер и охотник будут иметь трудный следующий год. Переговорный процесс продолжается, рыночный процесс изменения агентами их котировок отражает его ход. Как результат, позиции рыночных агентов сходятся, и они совпадают в момент времени t1E, который соответствует точке пересечения траекторий E1 на графиках.

На взаимовыгодных условиях в момент времени t1E осуществляется добровольная сделка. Далее рынок снова погружается в состояние покоя до следующего урожая и выставления его на продажу в следующем году в момент времени t2.

Предположим, для определенности, что урожай в новом сезоне вырос, поэтому qS(t2) >qS(t1). В этом случае продавец, очевидно, вынужден сразу установить стартовую цену ниже,

pS(t2) < pS(t1), пока покупатель, воспользовавшись возможностью, также понижает цену и увеличивает свое количество зерна: pD(t2) < pD(t1) и qD(t2) > qD(t1). В этом случае естественно ожидать, что траектории покупателя и продавца будут немного различаться, и соглашение между покупателем и продавцом будет достигаться с другими параметрами, чем в предыдущий раунд торгов.

Условно мы будем описывать ситуацию на рынке в каждый момент времени с помощью множества реальных рыночных цен и количеств реальных сделок, которые действительно происходят на рынке. Как видно из рис. 1.3, в нашей модели реальные сделки происходят на рынке только в такие моменты времени, например, t1E и t2E когда справедливы следующие условия рыночного равновесия (точки E1 на рис. 1.3):

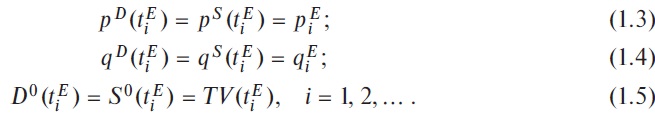
1.6.3. КОНЦЕПЦИЯ СПРОСА И ПРЕДЛОЖЕНИЯ В КЛАССИКЕ

В формулах (1.3)-(1.5) мы использовали несколько новых понятий и определений, смысл которых требует разъяснения. Мы представим его довольно подробно, поскольку это важно для понимания последующего изложения теории. Во-первых, в современной экономической теории концепция S&D играет одну из центральных ролей. То же самое относится и к вероятностной экономической теории, которую, как мы говорили выше, в определенной мере можно трактовать как теорию спроса и предложения. Интуитивно, на качественном описательном уровне все экономисты понимают, что означает эта концепция. Сложности и расхождения появляются только на практике при попытках дать математическое толкование этим понятиям и развить адекватный метод их вычисления и измерения. Для этой цели были развиты различные теории, содержащие разные математические модели S&D. В этих теориях различные функции S&D используются для формального определения и количественного описания S&D.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.