William Oughtred

Of English eighteenth-century authors the following still clung to the notation A.B::C.D: John Harris’ translation of F. Ignatius Gaston Pardies (1701),102 George Shelley (1704),103 Sam Cobb (1709),104 J. Collins in Commercium Epistolicum (1712), John Craig (1718),105 Jo. Wilson (1724).106 The latest use of A.B::C.D which has come to our notice is in the translation of the Analytical Institutions of Maria G. Agnesi, made by John Colson sometime before 1760, but which was not published until 1801. During the seventeenth century the notation A:B::C:D acquired almost complete ascendancy in England.

In France Oughtred’s unmodified notation A.B::C.D, having been adopted later, was also discarded later than in England. An approximate idea of the situation appears from the following data. The notation A.B::C.D was used by M. Carré (1700),107 M. Guisnée (1705),108 M. de Fontenelle (1727),109 M. Varignon (1725),110 M. Robillard (1753),111 M. Sebastien le Clerc (1764),112 Clairaut (1731),113 M. L’Hospital (1781).114

In Italy Oughtred’s modified notation a, b::c, d was used by Maria G. Agnesi in her Instituzioni analitiche, Milano, 1748. The notation a:b::c:d found entrance the latter part of the eighteenth century. In Germany the symbolism a:b=c:d, suggested by Leibniz, found wider acceptance.115

It is evident from the data presented that Oughtred proposed his notation for ratio and proportion at a time when the need of a specific notation began to be generally felt, that his symbol for ratio a.b was temporarily adopted in England and France but gave way in the eighteenth century to the symbol a:b, that Oughtred’s symbol for proportion :: found almost universal adoption in England and France and was widely used in Italy, the Netherlands, the United States, and to some extent in Germany; it has survived to the present time but is now being gradually displaced by the sign of equality =.

Oughtred’s notation to express aggregation of terms has received little attention from historians but is nevertheless interesting. His books, as well as those of John Wallis, are full of parentheses but they are not used as symbols of aggregation in algebra; they are simply marks of punctuation for parenthetical clauses. We have seen that Oughtred writes (a+b)² and √a+b thus, Q:a+b:, √:a+b:, or Q:a+b, √:a+b, using on rarer occasions a single dot in place of the colon. This notation did not originate with Oughtred, but, in slightly modified form, occurs in writings from the Netherlands. In 1603 C. Dibvadii in geometriam Evclidis demonstratio numeralis, Leyden, contains many expressions of this sort, √·136+√2048, signifying √(136+√2048). The dot is used to indicate that the root of the binomial (not of 136 alone) is called for. This notation is used extensively in Ludolphi à Cevlen de circulo, Leyden, 1619, and in Willebrordi Snellii De circuli dimensione, Leyden, 1621. In place of the single dot Oughtred used the colon (:), probably to avoid confusion with his notation for ratio. To avoid further possibility of uncertainty he usually placed the colon both before and after the algebraic expression under aggregation. This notation was adopted by John Wallis and Isaac Barrow. It is found in the writings of Descartes. Together with Vieta’s horizontal bar, placed over two or more terms, it constituted the means used almost universally for denoting aggregation of terms in algebra. Before Oughtred the use of parentheses had been suggested by Clavius116 and Girard.117 The latter wrote, for instance, √(2+√3). While parentheses never became popular in algebra before the time of Leibniz and the Bernoullis they were by no means lost sight of. We are able to point to the following authors who made use of them: I. Errard de Bar-le-Duc (1619),118 Jacobo de Billy (1643),119 one of whose books containing this notation was translated into English, and also the posthumous works of Samuel Foster.120 J. W. L. Glaisher points out that parentheses were used by Norwood in his Trigonometrie (1631), p. 30.121

The symbol for the arithmetical difference between two numbers, ~, is usually attributed to John Wallis, but it occurs in Oughtred’s Clavis mathematicae of 1652, in the tract on Elementi decimi Euclidis declaratio, at an earlier date than in any of Wallis’ books. As Wallis assisted in putting this edition through the press it is possible, though not probable, that the symbol was inserted by him. Were the symbol Wallis’, Oughtred would doubtless have referred to its origin in the preface. During the eighteenth century the symbol found its way into foreign texts even in far-off Italy.122 It is one of three symbols presumably invented by Oughtred and which are still used at the present time. The others are × and ::.

The curious and ill-chosen symbols,

for “greater than,” and

for “less than,” were certain to succumb in their struggle for existence against Harriot’s admirably chosen > and <. Yet such was the reputation of Oughtred that his symbols were used in England quite extensively during the seventeenth and the beginning of the eighteenth century. Considerable confusion has existed among algebraists and also among historians as to what Oughtred’s symbols really were. Particularly is this true of the sign for “less than” which is frequently written

. Oughtred’s symbols, or these symbols turned about in some way, have been used by Seth Ward,123 John Wallis,124 Isaac Barrow,125 John Kersey,126 E. Wells,127 John Hawkins,128 Tho. Baker,129 Richard Sault,130 Richard Rawlinson,131 Franciscus Dulaurens,132 James Milnes,133 George Cheyne,134 John Craig,135 Jo. Wilson,136 and J. Collins.137

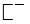
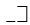
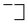
General acceptance has been accorded to Oughtred’s symbol ×. The first printed appearance of this symbol for multiplication in 1618 in the form of the letter x hardly explains its real origin. The author of the “Appendix” (be he Oughtred or someone else) may not have used the letter x at all, but may have written the cross ×, called the St. Andrew’s cross, while the printer, in the absence of any type accurately representing that cross, may have substituted the letter x in its place. The hypothesis that the symbol × of multiplication owes its origin to the old habit of using directed bars to indicate that two numbers are to be combined, as for instance in the multiplication of 23 and 34, thus,

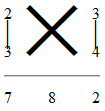
has been advanced by two writers, C. Le Paige138 and Gravelaar.139 Bosmans is more inclined to the belief that Oughtred adopted the symbol somewhat arbitrarily, much as he did the numerous symbols in his Elementi decimi Euclidis declaratio.140

Le Paige’s and Gravelaar’s theory finds some support in the fact that the cross ×, without the two additional vertical lines shown above, occurs in a commentary published by Oswald Schreshensuchs141 in 1551, where the sign is written between two factors placed one above the other.

CHAPTER V

OUGHTRED’S IDEAS ON THE TEACHING OF MATHEMATICS

GENERAL STATEMENT

Nowhere has Oughtred given a full and systematic exposition of his views on mathematical teaching. Nevertheless, he had very pronounced and clear-cut ideas on the subject. That a man who was not a teacher by profession should have mature views on teaching is most interesting. We gather his ideas from the quality of the books he published, from his prefaces, and from passages in his controversial writing against Delamain. As we proceed to give quotations unfolding Oughtred’s views, we shall observe that three points receive special emphasis: (1) an appeal to the eye through suitable symbolism; (2) emphasis upon rigorous thinking; (3) the postponement of the use of mathematical instruments until after the logical foundations of a subject have been thoroughly mastered.

The importance of these tenets is immensely reinforced by the conditions of the hour. This voice from the past speaks wisdom to specialists of today. Recent methods of determining educational values and the modern cult of utilitarianism have led some experts to extraordinary conclusions. Laboratory methods of testing, by the narrowness of their range, often mislead. Thus far they have been inferior to the word of a man of experience, insight, and conviction.

MATHEMATICS, “A SCIENCE OF THE EYE”

Oughtred was a great admirer of the Greek mathematicians – Euclid, Archimedes, Apollonius of Perga, Diophantus. But in reading their works he experienced keenly what many modern readers have felt, namely, that the almost total absence of mathematical symbols renders their writings unnecessarily difficult to read. Statements that can be compressed into a few well-chosen symbols which the eye is able to survey as a whole are expressed in long-drawn-out sentences. A striking illustration of the importance of symbolism is afforded by the history of the formula

ix=log(cos x+i sin x).

It was given in Roger Cotes’ Harmonia mensurarum, 1722, not in symbols, but expressed in rhetorical form, destitute of special aids to the eye. The result was that the theorem remained in the book undetected for 185 years and was meanwhile rediscovered by others. Owing to the prominence of Cotes as a mathematician it is very improbable that such a thing could have happened had the theorem been thrust into view by the aid of mathematical symbols.

In studying the ancient authors Oughtred is reported to have written down on the margin of the printed page some of the theorems and their proofs, expressed in the symbolic language of algebra.

In the preface of his Clavis of 1631 and of 1647 he says:

Wherefore, that I might more clearly behold the things themselves, I uncasing the Propositions and Demonstrations out of their covert of words, designed them in notes and species appearing to the very eye. After that by comparing the divers affections of Theorems, inequality, proportion, affinity, and dependence, I tryed to educe new out of them.

It was this motive which led him to introduce the many abbreviations in algebra and trigonometry to which reference has been made in previous pages. The pedagogical experience of recent centuries has indorsed Oughtred’s view, provided of course that the pupil is carefully taught the exact meaning of the symbols. There have been and there still are those who oppose the intensive use of symbolism. In our day the new symbolism for all mathematics, suggested by the school of Peano in Italy, can hardly be said to be received with enthusiasm. In Oughtred’s day symbolism was not yet the fashion. To be convinced of this fact one need only open a book of Edmund Gunter, with whom Oughtred came in contact in his youth, or consult the Principia of Sir Isaac Newton, who flourished after Oughtred. The mathematical works of Gunter and Newton, particularly the former, are surprisingly destitute of mathematical symbols. The philosopher Hobbes, in a controversy with John Wallis, criticized the latter for that “Scab of Symbols,” whereupon Wallis replied:

I wonder how you durst touch M. Oughtred for fear of catching the Scab. For, doubtlesse, his book is as much covered over with the Scab of Symbols, as any of mine… As for my Treatise of Conick Sections, you say, it is covered over with the Scab of Symbols, that you had not the patience to examine whether it is well or ill demonstrated.142

Oughtred maintained his view of the importance of symbols on many different occasions. Thus, in his Circles of Proportion, 1632, p. 20:

This manner of setting downe Theoremes, whether they be Proportions, or Equations, by Symboles or notes of words, is most excellent, artificiall, and doctrinall. Wherefore I earnestly exhort every one, that desireth though but to looke into these noble Sciences Mathematicall, to accustome themselves unto it: and indeede it is easie, being most agreeable to reason, yea even to sence. And out of this working may many singular consectaries be drawne: which without this would, it may be, for ever lye hid.

RIGOROUS THINKING AND THE USE OF INSTRUMENTS

The author’s elevated concept of mathematical study as conducive to rigorous thinking shines through the following extract from his preface to the 1647 Clavis:

… Which Treatise being not written in the usuall synthetical manner, nor with verbous expressions, but in the inventive way of Analitice, and with symboles or notes of things instead of words, seemed unto many very hard; though indeed it was but their owne diffidence, being scared by the newnesse of the delivery; and not any difficulty in the thing it selfe. For this specious and symbolicall manner, neither racketh the memory with multiplicity of words, nor chargeth the phantasie with comparing and laying things together; but plainly presenteth to the eye the whole course and processe of every operation and argumentation.

Now my scope and intent in the first Edition of that my Key was, and in this New Filing, or rather forging of it, is, to reach out to the ingenious lovers of these Sciences, as it were Ariadnes thread, to guide them through the intricate Labyrinth of these studies, and to direct them for the more easie and full understanding of the best and antientest Authors… That they may not only learn their propositions, which is the highest point of Art that most Students aime at; but also may perceive with what solertiousnesse, by what engines of aequations, Interpretations, Comparations, Reductions, and Disquisitions, those antient Worthies have beautified, enlarged, and first found out this most excellent Science… Lastly, by framing like questions problematically, and in a way of Analysis, as if they were already done, resolving them into their principles, I sought out reasons and means whereby they might be effected. And by this course of practice, not without long time, and much industry, I found out this way for the helpe and facilitation of Art.

Still greater emphasis upon rigorous thinking in mathematics is laid in the preface to the Circles of Proportion and in some parts of his Apologeticall Epistle against Delamain. In that preface William Forster quotes the reply of Oughtred to the question how he (Oughtred) had for so many years concealed his invention of the slide rule from himself (Forster) whom he had taught so many other things. The reply was:

That the true way of Art is not by Instruments, but by Demonstration: and that it is a preposterous course of vulgar Teachers, to begin with Instruments, and not with the Sciences, and so in-stead of Artists, to make their Scholers only doers of tricks, and as it were Iuglers: to the despite of Art, losse of previous time, and betraying of willing and industrious wits, vnto ignorance, and idlenesse. That the vse of Instruments is indeed excellent, if a man be an Artist: but contemptible, being set and opposed to Art. And lastly, that he meant to commend to me, the skill of Instruments, but first he would haue me well instructed in the Sciences.”

Delamain took a different view, arguing that instruments might very well be placed in the hands of pupils from the start. At the time of this controversy Delamain supported himself by teaching mathematics in London and he advertised his ability to give instruction in mathematics, including the use of instruments. Delamain brought the charge against Oughtred of unjustly calling “many of the [British] Nobility and Gentry doers of trickes and juglers.” To this Oughtred replies:

As I did to Delamain and to some others, so I did to William Forster: I freely gave him my helpe and instruction in these faculties: only this was the difference, I had the very first moulding (as I may say) of this latter: But Delamain was already corrupted with doring upon Instruments, and quite lost from ever being made an Artist: I suffered not William Forster for some time so much as speake of any Instrument, except only the Globe it selfe; and to explicate, and worke the questions of the Sphaere, by the way of the Analemma: which also himselfe did describe for the present occasion. And this my restraint from such pleasing avocations, and holding him to the strictnesse of percept, brought forth this fruit, that in short time, even by his owne skill, he could not onely use any Instrument he should see, but also was able to delineate the like, and devise others.143

As representing Delamain’s views, we make the following selection from his Grammelogia (London, about 1633), the part near the end of the book and bearing the title, “In the behalfe of vulgar Teachers and others,” where Delamain refers to Oughtred’s charge that the scholars of “vulgar” teachers are “doers of tricks, as it were iuglers.” Delamain says:

… Which words are neither cautelous, nor subterfugious, but are as downe right in their plainnesse, as they are touching, and pernitious, by two much derogating from many, and glancing upon many noble personages, with too grosse, if not too base an attribute, in tearming them doers of tricks, as it were to iuggle: because they perhaps make use of a necessitie in the furnishing of themselves with such knowledge by Practicall Instrumentall operation, when their more weighty negotiations will not permit them for Theoreticall figurative demonstration; those that are guilty of the aspertion, and are touched therewith may answer for themselves, and studie to be more Theoreticall, than Practicall: for the Theory, is as the Mother that produceth the daughter, the very sinewes and life of Practise, the excellencie and highest degree of true Mathematicall Knowledge: but for those that would make but a step as it were into that kind of Learning, whose onely desire is expedition, and facilitie, both which by the generall consent of all are best effected with Instrument, rather then with tedious regular demonstrations, it was ill to checke them so grosly, not onely in what they have Practised, but abridging them also of their liberties with what they may Practise, which aspertion may not easily be slighted off by any glosse or Apologie, without an Ingenuous confession, or some mentall reservation: To which vilification, howsoever, in the behalfe of my selfe, and others, I answer; That Instrumentall operation is not only the Compendiating, and facilitating of Art, but even the glory of it, whole demonstration both of the making, and operation is soly in the science, and to an Artist or disputant proper to be knowne, and so to all, who would truly know the cause of the Mathematicall operations in their originall; But, for none to know the use of a Mathematicall Instrumen[t], except he knowes the cause of its operation, is somewhat too strict, which would keepe many from affecting the Art, which of themselves are ready enough every where, to conceive more harshly of the difficultie, and impossibilitie of attayning any skill therein, then it deserves, because they see nothing but obscure propositions, and perplex and intricate demonstrations before their eyes, whose unsavoury tartnes, to an unexperienced palate like bitter pills is sweetned over, and made pleasant with an Instrumentall compendious facilitie, and made to goe downe the more readily, and yet to retaine the same vertue, and working; And me thinkes in this queasy age, all helpes may bee used to procure a stomacke, all bates and invitations to the declining studie of so noble a Science, rather then by rigid Method and generall Lawes to scarre men away. All are not of like disposition, neither all (as was sayd before) propose the same end, some resolve to wade, others to put a finger in onely, or wet a hand: now thus to tye them to an obscure and Theoricall forme of teaching, is to crop their hope, even in the very bud… The beginning of a mans knowledge even in the use of an Instrument, is first founded on doctrinal precepts, and these precepts may be conceived all along in its use: and are so farre from being excluded, that they doe necessarily concomitate and are contained therein: the practicke being better understood by the doctrinall part, and this later explained by the Instrumentall, making precepts obvious unto sense, and the Theory going along with the Instrument, better informing and inlightning the understanding, etc. vis vnita fortior, so as if that in Phylosophy bee true, Nihil est [in] intellectu quod non prius fuit in sensu.

The difference between Oughtred and Delamain as to the use of mathematical instruments raises important questions. Should the slide rule be placed in the hands of a boy before, or after, he has mastered the theory of logarithms? Should logarithmic tables be withheld from him until the theoretical foundation is laid in the mind of the pupil? Is it a good thing to let a boy use a surveying instrument unless he first learns trigonometry? Is it advisable to permit a boy to familiarize himself with the running of a dynamo before he has mastered the underlying principles of electricity? Does the use of instruments ordinarily discourage a boy from mastery of the theory? Or does such manipulation constitute a natural and pleasing approach to the abstract? On this particular point, who showed the profounder psychological insight, Oughtred or Delamain?

In July, 1914, there was held in Edinburgh a celebration of the three-hundredth anniversary of the invention of logarithms. On that occasion there was collected at Edinburgh university one of the largest exhibits ever seen of modern instruments of calculation. The opinion was expressed by an experienced teacher that “weapons as those exhibited there are for men and not for boys, and such danger as there may be in them is of the same character as any form of too early specialization.”

It is somewhat of a paradox that Oughtred, who in his student days and during his active years felt himself impelled to invent sun-dials, planispheres, and various types of slide rules – instruments which represent the most original contributions which he handed down to posterity – should discourage the use of such instruments in teaching mathematics to beginners. That without the aid of instruments he himself should have succeeded so well in attracting and inspiring young men constitutes the strongest evidence of his transcendent teaching ability. It may be argued that his pedagogic dogma, otherwise so excellent, here goes contrary to the course he himself followed instinctively in his self-education along mathematical lines. We read that Sir Isaac Newton, as a child, constructed sun-dials, windmills, kites, paper lanterns, and a wooden clock. Should these activities have been suppressed? Ordinary children are simply Isaac Newtons on a smaller intellectual scale. Should their activities along these lines be encouraged or checked?

On the other hand, it may be argued that the paradox alluded to above admits of explanation, like all paradoxes, and that there is no inconsistency between Oughtred’s pedagogic views and his own course of development. If he invented sun-dials, he must have had a comprehension of the cosmic motions involved; if he solved spherical triangles graphically by the aid of the planisphere, he must have understood the geometry of the sphere, so far as it relates to such triangles; if he invented slide rules, he had beforehand a thorough grasp of logarithms. The question at issue does not involve so much the invention of instruments, as the use by the pupil of instruments already constructed, before he fully understands the theory which is involved. Nor does Sir Isaac Newton’s activity as a child establish Delamain’s contention. Of course, a child should not be discouraged from manual activity along the line of producing interesting toys in imitation of structures and machines that he sees, but to introduce him to the realm of abstract thought by the aid of instruments is a different proposition, fraught with danger. A boy may learn to use a slide rule mechanically and, because of his ability to obtain practical results, feel justified in foregoing the mastery of underlying theory; or he may consider the ability of manipulating a surveying instrument quite sufficient, even though he be ignorant of geometry and trigonometry; or he may learn how to operate a dynamo and an electric switchboard and be altogether satisfied, though having no grasp of electrical science. Thus instruments draw a youth aside from the path leading to real intellectual attainments and real efficiency; they allure him into lanes which are often blind alleys. Such were the views of Oughtred.