Генезис и структура квалитативизма Аристотеля

Как только Платон начинает излагать геометрическую теорию стихий-элементов, он сразу же, можно сказать, берет эти свои слова обратно: «Мы обязаны более четко, – говорит он, – определить одну вещь, о которой прежде говорилось, неясно. В самом деле, нам казалось, будто все четыре рода могут последовательно перерождаться друг в друга, но такая видимость была неправильной» (там же, 54b 8 – c 1, курсив наш. – В.В.). То, что ранее было выражено вполне ясно и отчетливо в контексте экспликации понятия материи, теперь Платону кажется смутным; то, что казалось теоретически обоснованным выражением сути физических отношений изменяющихся стихий, теперь предстает как «неправильная видимость». Чем объясняется такая неожиданно резкая самокритика? Она объясняется тем, что в этом месте Платон приступает к изложению геометрической теории элементов. Аргументы геометрического плана, вынуждающие внести фундаментальную асимметрию во внутреннюю структуру стихий (приписывание земле в отличие от остальных элементов в качестве элементарного прямоугольного равнобедренного треугольника), являются для Платона гораздо более сильными, чем представления об элементах как равноправных состояниях материи. Аристотель, кстати, разовьет и усовершенствует понятие первоматерии, определив элементы через наложение на первоматерию основных элементарных качеств. Однако геометрическую теорию элементов он отбросит как совершенно неприемлемую для его понимания физики вообще и особенно ее взаимосвязи с математикой.

Итак, для нас важно констатировать то обстоятельство, что «безбарьерная» взаимопревращаемость элементов нарушается, как только вводится принцип геометрической структуры и основанного на нем различия в строении стихий. Чисто математическая асимметрия определяет физическую асимметрию. Взаимная превращаемость стихий ограниченна, поскольку вводится математический принцип, упорядочивающий хаотическую динамику стихий «с помощью образов и чисел» (Тимей, 53b 6–7).

Сопоставление этих двух сталкивающихся между собой в противоречии мест показывает, что на стороне традиционного представления – обыденный опыт. Чтобы убедиться в этом, достаточно еще раз прочитать эмпирически достоверное описание взаимопревращений стихий. Характерно, что эти переходы обусловлены единым механизмом сгущения – разрежения (предложенным еще Анаксименом), который реализуется в конкретно-метеорологической форме (облака и тучи, дождь, ветер, возгорание воздуха и т. д.). На стороне же нового представления об ограниченной превращаемости стихий – только геометрические необходимости. Поскольку такой род аргументации предпочитается Платоном и для него несравненно более «правилен» и «ясен», постольку его программу построения физического знания действительно можно назвать математической. Ее поддерживает лишь математическая теория и убеждение в том, что она-то и составляет основу физического мира. Напротив, на стороне соперничающей с ней нематематической программы – традиция, здравый смысл и опыт и, конечно, новая философия, онтология и теория знания.

Критика Аристотелем платоновской теории вещества была несомненно чрезвычайно плодотворной уже в том только отношении, что она вызвала лавинообразно нарастающее – и не смолкающее до сих пор – комментирование, истолкование, объяснение ее трудностей и неясностей. Эта критика способствовала развитию самой теории, усовершенствованию ее защитниками платонизма. Множество комментаторов пытались дать платоновским элементам такое истолкование, которое бы отбросило основные критические замечания Аристотеля. Это касается прежде всего аристотелевского сомнения в возможности объяснения качеств из «бескачественных» фигур, например, объяснения такого физического свойства, как вес, из невесомых «плоскостей».

Основные затруднения этой теории – в разрыве между геометрией и физикой. Поэтому платоновские треугольники интерпретируются как материальные тонкие пластинки. Видимо, впервые такую интерпретацию дал Мартин: «Мы рассматриваем треугольники и квадраты Платона, – говорит он, – как тонкие листки телесной материи» [28, c. 242]. По существу эту же мысль высказывает и Ева Закс: «Нельзя отрицать, – подчеркивает она, – что треугольники, из которых Платон “составляет” тела, сами являются телами» [118, с. 215]. Однако такая интерпретация была подвергнута критике, потому что не слишком хорошо согласовывалась с текстом «Тимея» и с духом платоновского учения вообще [121, с. 9]. Кроме того, надо учесть изменения в самой физике, которые также, несомненно, способствовали эволюции в интерпретации геометрической теории Платона. Новые интерпретации развивают, с одной стороны, динамические истолкования платоновских фигур, а с другой стороны, дают им статус формальных, идеальных компонент или принципов. Согласно Мюглеру, «στοιχεῖον Платона – это оказывающая сопротивление поверхность, поле сил: в таком случае ни пустота внутри элементарных полиэдров, ни проблема веса не приводят больше к затруднениям» [106, с. 121]. Такое же стремление отвести критическую аргументацию Аристотеля мы находим и у Клэгхорна. Разбирая критическое замечание Аристотеля, указывающего на невозможность образования физического тела из математической поверхности, Клэгхорн говорит, что «Платон должен был бы согласиться с этим, так как плоскости прежде всего несут объяснительную функцию и нет указаний на то, что они сами по себе образуют реальность. Они указывают на границы тела и дают поверхность платоновской материи (receptacle), внутри которой нечто должно возникнуть» [44, с. 31].

Истолкование платоновских треугольников в свете понятия формы идет, видимо, от Арчера-Хайнда, который стремился соединить реальный и формальный моменты: «Плоскости, – говорит он, – являются реальными плоскостями, но они не образуют тела, а выражают просто закон их образования» [28, с. 204]. Более последовательно эту точку зрения проводит Корнфорд, истолковывая платоновские треугольники в свете платоновской же теории идеи: «Фигуры, – подчеркивает он, – не являются действительными формами реально существующих частиц, которые могут быть только несовершенными копиями, но они являются совершенными типами, относящимися к умопостигаемому миру математики» [48, 210]. Интересную интерпретацию платоновского учения об элементах дает Морроу. Он считает, что в «Тимее» содержится иное по форме учение об идеях-формах, чем в таких диалогах, как «Государство» или «Федон». Но теория вещества, представления об элементарных треугольниках излагаются в свете этого учения на знакомом языке подражания и причастия, образца и копии.

«Так как чувственные свойства, – говорит Морроу, – “подобны” их объективным причинам, – т. е. подобны им в смысле изоморфизма, имеющегося между ними и их коррелятами в чувственно невоспринимаемых телах, – и так как эти чувственно невоспринимаемые частицы сами являются подражаниями математическим полиэдрам, то чувственно данный мир дважды становится миром подражания умопостигаемым математическим формам» [105, с. 26].

«Приобщение», оформляющее физический мир «макрообъектов», осуществляется в две стадии: во-первых, невидимые частицы вещества «подражают» «чисто» математическим объектам, а во-вторых, физическое явление «копирует» свойства частиц. В этих интерпретациях исследователей продолжается полемический диалог Аристотеля с Платоном. Развитие науки лишь обогащает основной предмет спора: как же создается физический мир, из каких основ?

§ 2. Критика геометрической теории

Критике платоновской теории вещества Аристотель посвящает первую главу III книги «О небе». В этой книге он рассматривает подлунный мир, его устройство и разбирает проблему генезиса тел в свете теории элементов. Тела надлунного мира вечны, они не возникают и не разрушаются. Но тела подлунного мира возникают. Поэтому встает вопрос о механизмах их возникновения.

Аристотель вычленяет ряд подходов к решению этого вопроса: элеаты, Гесиод и древнейшие физики, Гераклит и примыкающие к нему философы, наконец, Платон. Существуют и иные подходы, но о них Аристотель говорит в других сочинениях, в частности в «Физике» и «Метафизике». Любопытно, что самое первое критическое замечание Аристотеля в адрес платоновской теории – это указание на ее несоответствие математике: «Самое поверхностное наблюдение, – говорит Стагирит, – показывает, что эта теория находится в противоречии по многим пунктам с математическими истинами» (О небе, III, 1, 299а 4–5). Аристотель хочет «побить» Платона его собственным оружием – математикой.

В чем же состоят эти математические истины, на которые ссылается Аристотель? Согласно Аристотелю, математические истины противоречат тому утверждению, что из неделимых элементов можно образовать делимые объекты. Аристотель отсылает здесь читателя или слушателя к трактату «О движении», т. е. к «Физике» (Физика, VI, 1,2). В «Физике» Аристотель показывает, что неделимые элементы длины не существуют. Он говорит, резюмируя свой анализ, что «ничто непрерывное не является лишенным частей» (Физика, VI, 2, 233b 34). Длина же, как и время, – непрерывны. Итак, «математический» аргумент Аристотеля против платоновской геометрической теории вещества состоит в указании на то, что математические объекты непрерывны и делимы. Платон же допускает существование таких элементарных и, следовательно, неделимых объектов, как линии и треугольники, представляющие части поверхности, ограниченной этими линиями.

Более развернутую аргументацию Аристотель дает, рассматривая проблему возникновения тел из элементов в физическом плане. Основной предпосылкой, на которой базируется вся критика Аристотелем платоновской теории, служит допущение о делимости и, следовательно, непрерывности свойств или качеств физических объектов. «Все свойства тел являются делимыми», – говорит Аристотель (О небе, III, 1, 299а 19).

Делимость свойств сталкивается с неделимостью элементов: делимое не может быть атрибутом неделимого. А поэтому теория, исходящая из неделимых элементов, не может, как считает Аристотель, объяснить свойства тел, их качества. Аристотель здесь расчленяет понятие делимости на специфическую делимость, делимость по виду (κατ’ εἶδος) и делимость по совпадению (κατὰ συμβεβηκός). Делимость по виду – это делимость рода на виды, например, цвет как род делится на белое и черное как его основные элементарные виды. Очевидно, что в анализе вопроса о генезисе тел речь идет о делимости по совпадению. Так, например, такие свойства, как вес, делимы по совпадению: деление тела – носителя веса – означает делимость по совпадению и самого веса как свойства этого тела. Теория Платона, предполагая неделимые, исключает из сферы элементов физического мира все свойства, подобные весу, все свойства, делимые по совпадению. Но и в этом случае она бессильна объяснить эти свойства, данность которых непосредственно засвидетельствована опытом, чувственным восприятием. Действительно, если платоновские неделимые объекты обладают весом, то они не неделимы. Но если они невесомы, то как из невесомых элементов могут возникнуть весомые физические тела? Логика аристотелевского мышления не может допустить возникновения свойств макротел при условии их отсутствия в фундаменте физического мира. Добавим, что делимость веса выводится Аристотелем на основе анализа эмпирической относительности понятия веса: одни тела более весомы, чем другие, причем никаких ограничений этой относительности в опыте не содержится.

Мы можем сказать, заключая наше рассмотрение физической аргументации Аристотеля против платоновской теории, что он не может принять разрыва между свойствами и качествами тел на «макроуровне» (объясняемый уровень, уровень явлений) и элементами или началами тел (объясняющий уровень, уровень сущности). Логика аристотелевского мышления, которую мы здесь обнаруживаем, состоит в том, что элементарная сущность, или основание, строится по подобию явления, им обосновываемого.

У Платона же наблюдается явный разрыв между свойствами и элементами. Действительно, свойства относительны и делимы, а элементы тел – неделимы. Неделимые элементы не могут быть носителями делимых свойств. Следовательно, заключает Аристотель, теория Платона несостоятельна. Эту же критику он считает правомерной и по отношению к пифагорейской концепции, согласно которой космос строится из чисел. «Действительно, – говорит Аристотель, – природные тела явным образом обладают тяжестью и легкостью, в то время как соединение единиц не может дать тела и не может обладать весом» (О небе, III, 1, 300а 17–20).

В седьмой главе III книги «О небе», разбирая механизм возникновения вещей в различных теориях элементов, Аристотель возвращается к критике платоновской теории в контексте анализа проблемы взаимопревращаемости элементов. Начинает он с критики теорий Эмпедокла и Демокрита, в которых «отрицается всякое взаимное порождение элементов» (О небе, III, 7, 305b 1–2). В этих теориях возникновение сводится к простому выделению, обособлению того, что уже ранее существовало, но в смешении с другим.

Затем Аристотель переходит к критическому разбору взглядов Платона и его сторонников. Слабым местом платоновской концепции Аристотель считает исключение земли из круга взаимных превращений элементов. У Платона такое исключение обусловлено тем, что элементарные треугольники, присущие земле, отличны от тех элементарных треугольников, из которых образуются другие стихии. Аристотель же считает такое построение нерациональным, противоречащим как логике ума, так и данным чувственного опыта, «согласно которому мы видим, что все элементы в равной мере превращаются одни в другие» (там же, 306а 4–5).

Таким образом, даваемое Платоном объяснение данных чувственного опыта не согласуется, как подчеркивает Аристотель, с самими этими данными (О небе, 306а 5–6). Причиной такого несоответствия между опытом и теоретическим построением, продолжает Аристотель, является несовершенство первых начал, или принципов, из которых при этом исходят, и дает такое пояснение: «Вероятно (ἴσως), – говорит он, – что для чувственно воспринимаемых вещей имеются чувственно воспринимаемые начала, для вещей вечных – вечные начала, для вещей преходящих – преходящие начала и, вообще, начала должны быть того же самого рода, что и их объекты» (там же, 306а 8–12, курсив наш. – В.В.). Такое утверждение само является методологическим принципом (началом). Этот принцип в иных выражениях Аристотель высказывает и во II книге «Физики» (195b 27–28). На первый взгляд может показаться, что требование, выставляемое здесь Аристотелем, исчерпывается требованием гомогенности, однородности объясняющего принципа и объекта объяснения. Но дело не в простой однородности, одноплановости этих двух сторон: важно заметить, что сама однородность определяется природой объясняемого объекта, что характер сущности фактически задается явлением. Платон и его сторонники неправы, – мы реконструируем ход мысли Аристотеля, – потому, что качества объясняют «бескачественным», в основу качественных явлений кладут количественные сущности, геометрические фигуры. Резюмируя всю III книгу «О небе», заключая ее восьмую главу, Аристотель говорит, что «наиболее существенные различия между телами – это различия в свойствах (κατά τὰ πάϑη), в функциях и силах (καί τά ἔργα καί τάς δυνάμεις), так как именно они характеризуют каждый природный объект» (III, 8,307b 20–24). Наиболее существенным, по Аристотелю, оказываются не фигуры, не числа, а сами качества, данные в чувственном опыте. Значит, у Аристотеля речь идет не о нейтральной гомогенности, а о вполне определенном превосходстве, или примате, чувственно воспринимаемых свойств, качеств, сил над уровнем сущности, уровнем принципов, начал и элементов, свободных от физической качественности. Различать тела и объяснять их поведение нужно не формой (геометрия) и не числом (арифметика), а свойствами, качествами и силами (аристотелевская физика).

Здесь необходимо сделать одно уточнение касательно понятий «фигура» и «качество». В «Категориях» Аристотель говорит, что «четвертый род качества образует фигура и присущая каждому предмету форма» (Категории, VIII, 10а 11). Значит ли это, что о противопоставлении фигуры и качества мы не можем говорить, так как фигура – один из видов качества? Качества, которые Аристотель противопоставляет здесь фигурам, это ποιότητες καὶ πάϑη, т. е. «пассивные качества и состояния» (Категории, VIII, 9а, 28), образующие третий род качеств согласно классификации «Категорий». Аристотель противопоставляет фигуре не качество вообще, а именно один из родов качества. К этому роду пассивных качеств и состояний он относит тепло, холод, сладость, горечь, кислое, белизну, черноту и все им сродное (там же).

Подчеркнем, что противопоставление фигуры и пассивного качества, или состояния (πάθος), вполне совместимо с классификацией качеств, изложенной в «Категориях». Кстати, более сжатая классификация качеств, даваемая в «Метафизике», согласуется с классификацией «Категорий» в данном отношении (Метафизика, V, 14).

Другая трудность платоновской теории, возникающая в связи с проблемой взаимопревращения элементов, состоит в том, что в ходе некоторых превращений должна оставаться в свободном виде некоторая часть исходных треугольников, что Аристотель считает иррациональным, непонятным (О небе, III, 7, 306а 23). Действительно, когда вода (20 элементарных треугольников) превращается в воздух (8 элементарных треугольников), то в результате превращения получаются две частицы воды (2x8) и остаются в свободном состоянии четыре треугольника (20 – 2x8 = 4). Это свободное или неопределенное состояние (παραιώρησις) для Аристотеля является иррациональным моментом. Здесь мы должны отметить, что у самого Платона не было этой «иррациональности», так как четыре треугольника, которые здесь имеются в виду, были для него одной частицей огня. Действительно, он говорит: «Вода, дробимая огнем или воздухом, позволяет образоваться одному телу огня и двум воздушным телам» (Тимей, 56d). Предположение о возможности такого состояния свободных треугольников, являющегося в определенных случаях вполне рациональным, мы находим у неоплатоника Прокла. Согласно Симпликию, Прокл утверждал, что при превращении трех частиц воздуха (8x3) в одну частицу воды (20) освобождаются четыре треугольника (8х3 – 20 = 4). Они не могут образовать одной частицы огня, так как все превращение направлено не вверх, а вниз, от воздуха к воде, и протекает как конденсация воздуха в воду охлаждением. Поэтому, утверждает Прокл, четыре треугольника должны оставаться в свободном, несвязанном состоянии. Соединяясь с двумя частицами воздуха, они дают одну частицу воды. Впрочем, Платон и сам признает возможность существования треугольников, по крайней мере, треугольников земли, в несвязанном состоянии. Так, он говорит о взаимодействии огня с землей: «Когда земля встречается с огнем и бывает развеяна его остротой, она стремительно несется, рассеиваясь либо в самом огне, либо в толще воздуха или воды, если ей придется там оказаться, покуда ее частицы, повстречавшись друг с другом, не соединятся сызнова, чтобы она опять стала землей» (Тимей, 56d). К этому вопросу мы еще вернемся в связи с анализом аргументов Прокла, выдвинутых им против Аристотеля в защиту теории Платона.

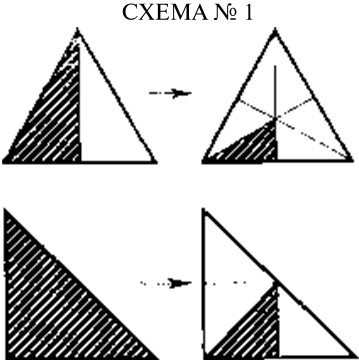
Наконец, последний аргумент Аристотеля в этой главе касается проблемы неделимости. Стагирит подчеркивает, что в то время как в математике предполагается делимость даже умопостигаемых объектов, в платоновской теории оказываются неделимыми физические тела (О небе, III, 7, 306а 26–29). Далее он «загоняет» Платона «в угол»: если же фигуры элементов делимы, то утрачивается гомогенность элементов, так как части пирамиды не есть пирамиды, а шар не делится на шары. Значит, или часть огня не есть огонь (фигура огня – пирамида или тетраэдр), или фигура неделима. Но ни одно, ни другое не может быть верным в логике аристотелевского мышления: стихии бесконечно делимы (любая часть огня есть огонь), как и фигуры. Неделимость фигур, говорит Аристотель, противоречит истинам математики (там же, 306а 28), а неоднородность элементов означает, что они не элементы, что предполагаются другие элементы, «тела более первичные» (там же, 306b 1). Это критическое замечание Аристотеля было отведено современными комментаторами[22]. Действительно, точка зрения Платона предполагает, что обычные так называемые элементы – земля, огонь, вода, воздух – это не настоящие элементы вещей. Мы не вправе считать их «буквами» мира и принимать за элементы, так как, подчеркивает Платон, «мало-мальски разумному человеку должно быть ясно, что нет никакого основания сравнивать их даже с каким-либо видом слогов» (Тимей, 48b). Начала вещей, их элементы у Платона – это треугольники двух видов, а не получающиеся из них многогранники. Интересно заметить, что Платон выбрал такие треугольники в качестве исходных, которые могут бесконечно делиться на подобные им треугольники с помощью простых геометрических построений. Более того, он сам в «Тимее» осуществляет такое дробление треугольников на подобные. Действительно, сначала Платон говорит, что исходным треугольником он считает тот, «который в соединении с подобным ему образует третий треугольник – равносторонний» (Тимей, 54а). Но в дальнейшем он уже говорит о другом, но подобном ему треугольнике, который, будучи сложен шесть раз (а не два), дает равносторонний треугольник (там же, 54е, см. верхнюю часть схемы № 1). Точно так же может делиться на более мелкие подобные ему треугольники и прямоугольный равнобедренный треугольник, образующий кубическую структуру земли (см. нижнюю часть схемы № 1). Конрфорд считает, что такое дробление и выбор более мелкого треугольника нужны Платону для того, чтобы иметь треугольники более мелких размеров для образования подвидов каждого первичного тела или элемента [48, c. 234–239].

В связи с этим моментом тезис Аристотеля о том, что пирамиды не могут делиться на пирамиды, что это так же смешно, как если бы «нож делился на ножи, а пилы – на пилы!» (О небе, III, 8, 307а 30–31), оказывается несостоятельным: платоновские треугольники (но, конечно, не правильные многогранники) вполне могут делиться на подобные себе треугольники.

В восьмой главе III книги «О небе» Аристотель продолжает свой критический анализ платоновской теории, подробно анализируя противоречия, возникающие при сведении элементов к геометрическим фигурам. Прежде всего он подчеркивает несоответствие между количеством фундаментальных геометрических фигур (2) и числом принятых элементов и (4) (306b 3–9). Далее Аристотель развивает интересную аргументацию, в основе которой мысль о том, что важнейшие характеристики элементов, и в частности их устойчивость, являются функциями местонахождения элемента. Критика эта направлена против платоновской концепции кубичности земли. Платон приписал земле форму куба, потому что земля – эмпирически самый устойчивый неподвижный элемент, а куб – самое устойчивое, трудно выводимое из равновесия геометрическое тело (вследствие своей повышенной по отношению, например, к тетраэдру симметрии). Но, говорит Аристотель, на своем естественном месте и огонь (тетраэдры) будет устойчивым и неподвижным, т. е. будет как бы кубом (307а 13). Согласно Аристотелю, положение элемента в системе естественных мест – вот что определяет его поведение и свойства, а не формы или фигуры.

Эта логика мышления, выдвигающего на первый план макроскопические, интегральные и феноменальные факторы вместо факторов микроскопических, дифференциальных и сущностных (как это имеет место у Платона и у атомистов), характерна и для другого аргумента Аристотеля. «Очевидно, – говорит Аристотель, – что все простые тела получают форму места, которое их охватывает, таковы именно вода и воздух» (306b 10–15). Воздействие внешнего тела таково, что форма элемента, находящегося в контакте с этим внешним телом (сосудом), не может сохраниться. Действительно, если это не так, то общая масса элемента, – рассуждает Аристотель, не будет находиться во всех своих точках в контакте с охватывающим ее телом и в таком случае не примет его форму. Но это противоречит опыту: вода в кувшине принимает форму кувшина. Об этом Аристотель не говорит, но предполагает этот факт как нечто само собой разумеющееся. Если же допустить, что фигуры элемента изменяются, то это уже не будет данный элемент, например вода. Опыт нам не говорит о том, что вода от контакта с кувшином становится другой стихией. Отсюда, заключает Аристотель, следует, что элементы не могут различаться фигурами.

Действительно, продолжает свою аргументацию Стагирит, среди фигур нет никакой противоположности (307b 6–7). И если огню приписывается форма шара (Демокрит) или пирамиды (Платон), то что же в таком случае следует приписать холоду, спрашивает Аристотель. И заключает свое рассуждение призывом к последовательности в мышлении: «Подобает, – говорит он, – или все силы объяснять фигурами, или ни одну из них не делать фигурой» (307b 9–10).