
Полная версия
Загадки космоса. Астрофизика

Загадки космоса
Астрофизика
Александр Золотов
© Александр Золотов, 2023
ISBN 978-5-0056-1539-8
Создано в интеллектуальной издательской системе Ridero
Аннотация
Существующая теория приливов и отливов, «обросла» разного рода домыслами, а реальных доказательств нет. В статье приводится ряд доказательств того, что у приливов совершенно другая природа, никак не связанная с гравитационным полем Луны, но признается, что Луна причастна к созданию приливов, более того, является их хранителем и гарантом. В статье приводится ряд мыслей и расчетов, объясняющих приливы.
Лунные приливы – это миф или реальность?
Попробуем разобраться в возможности действия Луны на приливы. Для дальнейшего разбирательства рассмотрим общую схему расположения Земли и Луны. Рисунок 1.
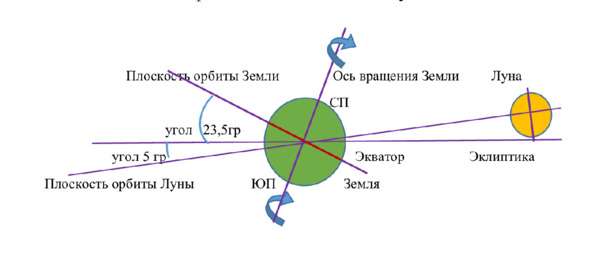
Рисунок 1.
На рисунке 1 изображены Земля, Луна, их плоскости орбит и углы между, ось вращения Земли и линия экватора. Все это поможет в дальнейшем понимать многие утверждения и предположения.
Как известно, направления вращений Земли и Луны по их орбитам – противоположные. Если мы остановим вращение Земли на одну секунду, то за это время Луна, при скорости 1,7км в сек, пролетит 1,7 км. Поверим в то, что Луна притягивает и увлекает за собой воду.
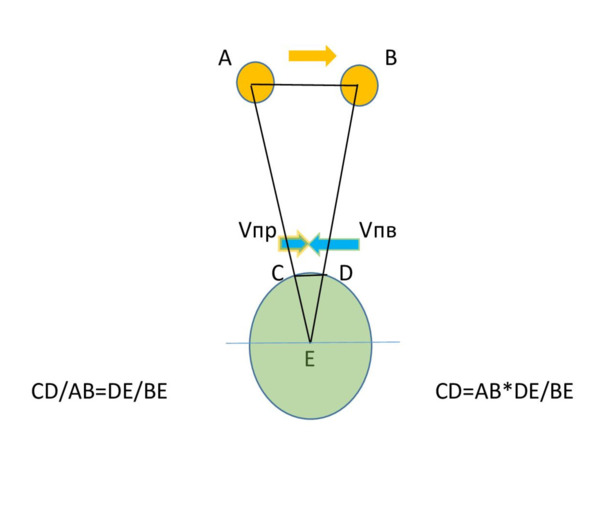
Рисунок 2
На рисунке 2 изображена схема, которая иллюстрирует полет Луны в интервале 1 секунда. Прямая АВ – это путь Луны за одну секунду. Скорость Луны у Земли в перигее равна 1.7км в сек. (первая космическая скорость для Луны) Легко подсчитать, что пройдённый Лунойпуть за дну секунду, будет 1.7 км.
Так же, для простоты расчета,проследим движение ОДНОГО килограмма воды, увлекаемого Луной. На рисунке 2, прямая CD – это расстояние килограмма воды заодну секунду. Из подобия треугольников определим отрезок СD
CD/AB=DE/BE CD=AB*DE/BE
Где: AB=1,7км/сек; DE = Rз = 6300км; BE =363000 (перигей) минимальное расстояние от Земли до Луны.
Имеющиеся данные подставим в формулу.
CD= 1,7км* 6300км/363000км = 0,029км=29м.
Определено расстояние (след), пройденное водой, которая движется под действием сил притяжения Луны, за одну секунду.
CD=29м.
Так как мы установили временной интервал в 1 сек, то скорость движения увлекаемой Луной воды-прилива, равна 29 м в сек. Vпр = 29 м в сек.
Известно, что скорость поверхности Земли на экваторе равна
Vпв=465 м в сек, но направление движения Луны не совпадает с плоскостью экватора, а значит, что и увлекаемый Луной поток воды не совпадает по направлению с направлением движения поверхностной воды. Если потоки не совпадают по направлению, то после из смешивания появится результирующий поток, который будет иметь свои характеристики.
Если взглянуть на рисунок 1, то станет ясно, что плоскость экватора не совпадает с плоскостью орбиты Луны, что дает основание полагать, что вектор движения поверхностной воды не совпадает с вектором потока воды, который увлекает за собой Луна. Этот угол равен более 28,5 градусов.
Другими словами, прилив направлен подуглом 28,5 градуса к направлению движения поверхностной воды. Скорость поверхностной воды на экваторе равна 465м/сек. В средних широтах эта скорость ниже. Примем – 375м/сек.
Vпв >> Vпр 375м/сек. >> 29м/сек.
Рассмотрим энергетику события. Формула кинетической энергии выглядит так.
Ек=mV2/2. Подставим величины скоростей в формулу. Напомним, что процесс рассматривается с для массы воды в1кг.
Eкпв = 1кг *3752/2=36156 кгм/сек2
Eкпр = 1кг *292/2 = 420 кгм/сек2.
Очевидно, что энергия движения поверхностной воды много больше энергии воды увлекаемой Луной.
Eкпв>> Eкпр 36156кгм/сек2>>420 кгм /сек2
Энергия движения одного килограмма поверхностной воды более чем в 80 раз больше энергии одного килограмма воды, увлекаемой Луной.
Встает вопрос, как случилось так, что 1кг воды с энергией 420 кгм/сек, преодолел энергию 1-го кг воды с энергией 36156кгм/сек?
Думается, что такая метаморфоза невозможна! Другими словами, поток поверхностной воды не даст двигаться воде за Луной.
Допустим, что мы ошиблись в расчетах, поэтому, я вынужден повторяться. Если силы притяжения Луны так сильны, что могут превзойти энергетику движения поверхностной воды, то почему, Луна не притянет воду облаков, воду, находящуюся в воздухе. А воды в воздухе, которым мы дышим, может быть равным 1,5 кг. в одном кубометре. Известно, что сила гравитации Солнца, действующая на Луну, больше чем сила Земли в 2 раза. Предлагаю маленький эксперимент. В лучах Солнца можно наблюдать пылинки, которые при отсутствии движения воздуха, практически неподвижны. В это же время можно увидеть Луну, среди яркого солнечного дня. Почему же пылинки абсолютно безучастны, как к Солнцу, так и к Луне. Ответ на поверхности. Потому, что лунные приливы – это выдумка, на фоне отсутствия понимания и объяснения приливов.
Рассмотрим еще один пример, доказывающий невозможность приливов на основе притяжения Луны. Рисунок 4.
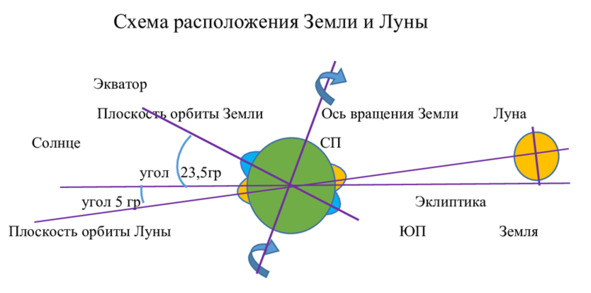
Рисунок 4.
Взглянем на схему расположения Луны и Земли. Утверждается, что Луна организует приливы в водоёмах Земли. В результате ее притяжения образуются водные бугры. Очевидно, что бугры, их максимум должны возникать в плоскости орбиты Луны. На схеме они изображены желтым цветом. Но образованные Луной бугры вызовут дисбаланс планеты, так как их расположение несимметрично оси вращения Земли. Балансировка планеты может сохраниться только в случае возникновения бугров, их максимум будет в плоскости экватора (на схеме синим цветом), но орбита движения Луны не совпадают с плоскостью экватора более чем на 28градусов. Вывод. Бугры – это досужий вымысел и полное непонимание процесса образования приливов. Еще несколько слов об отливе без прилива. Если последовать за нынешней теорией приливов, то окажется, что должен существовать отлив без прилива. Моделируем ситуацию. Луна находится над материком, проходит его, под ней берег моря. При ее дальнейшем движении, она начинает увлекать за собой воду, прибрежную воду. Начинается отлив. Возможно, подобное встречалось, но я такого не читал…. Рисунок 5.
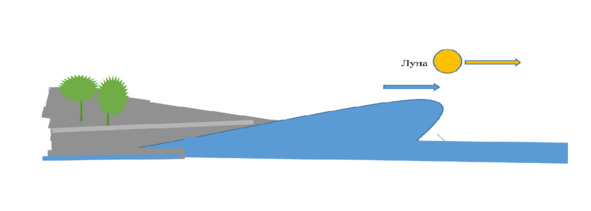
Рисунок 5.
Можно еще приводить примеры, которые не вписываются в действие гравитации Луны на воды Земли, но нельзя отрицать то, что приливы связаны с Луной. Обличать просто, но этого мало. Надо предложить обществу новую теорию, которая смола бы ответить на все вопросы.
В своей статье «Рождение и этапы эволюции Земли», я предположил, что центр тяжести у Луны смещен. Это обстоятельство, на мой взгляд, имеет решающее значение в формировании приливов.
Небесную механику трех тел, Солнца, Земли и Луны людям просчитать пока не удается, но можно с уверенностью сказать, что эти три тела (без учета гравитации остальных планет) находятся в динамическом равновесии. Изменение расстояния между ними не влияет на приливы. В противном случае огромные волны смыли бы все на поверхности Земли, но такого не происходит. Все компенсируется небесной механикой.
А если попробовать объяснить приливы через количество движения тел системы.
Количество движения в механической системе равна произведению массы на скорость, что выражается формулой.
Для одного вектора.
Q = M* V (1)
Для нескольких векторов количество движенияопределяется геометрической суммой векторов.
QMi* Vi (2)
Величины V- скорости векторные. Количеством механической системы называют векторную величину, равную геометрической сумме количеств движений всех точек данной системы.
Как это может быть? Рассмотрим систему Земля -Луна. Рисунок 6. Оба небесных тела находятся в движении. Поэтому каждое из них имеет определенное количество движения, имеет свой вектор, который меняется по величине скорости и направлению.
Луна движется вместе с Землей вокруг Солнца, ив тоже время, плоскости их орбит пересекается под углом около 28 градусов.Смотри рис. 6.
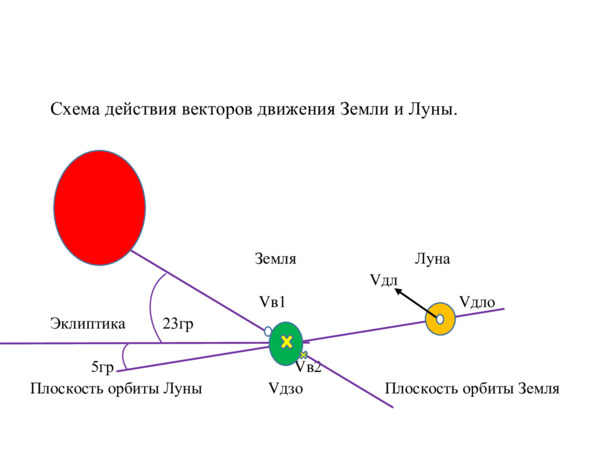
Рис. 6.
Рассмотрим схему векторов на рисунке 6.
Вектор количества движения Луны по орбите (Vдло) направлен по касательной к ней (белая точка).Второй лунный вектор количества движения (Vдл) всегда параллелен плоскости орбиты Земли, а когда Луна пересекает орбиту Земли, этот вектор совмещается с ней.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.





