 полная версия
полная версияМоделирование канала коротковолновой радиосвязи
По графику, приведенному в рекомендациях МСЭ-R P.372-9 рис.39 находим превышение напряжения помехи относительно медианного значения для заданной надежности связи А0(дБ). Переходя от (дБ) к (мкВ) имеем:
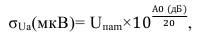
(37)
где Uпаm – медианное значение напряжения атмосферной помехи.
Поскольку напряжение помехи пропорционально напряженности поля в точке приема, то по аналогичной формуле можно определять превышение напряженности поля атмосферной помехи в точке приема относительно медианного значения:
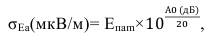
(38)
где Епam – медианное значение напряженности электрического поля атмосферной помехи в точке приема.
Действующее значение напряженности электрического поля атмосферной помехи в точке приема будет определяться по формуле:
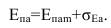
(39)
Соответственно, коэффициент пропорциональности ka для атмосферной помехи, определяемый по формуле (25), будет равен:
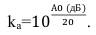
(40)
По формуле (27) определяем действующее значение атмосферной помехи на входе приемника при эквивалентной антенне, и по формуле (28) пересчитываем для реальной антенны.
Воспользовавшись формулой (33) можно найти медианное значение напряжения атмосферной помехи:
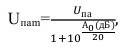
(41)
и среднеквадратическое отклонение амплитуды огибающей от медианного значения:
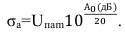
(42)
Амплитуда огибающей атмосферной помехи на входе приемника имеет логнормальное распределение.
По формулам (33) и (34) находим отношение с/ш на входе приемника, подключенного к антеннам полуволновой и волновой симметричный вибратор.
Расчет напряженности поля и отношения сигнал/шум для суммарной помехи
Отношение с/ш на входе приемника при воздействии суммарной помехи приближенно можно найти по формуле аналогичной (33) или (34):
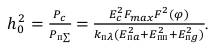
(43)
По формулам, приведенным в [3], можно определить воздействие суммарной помехи путем расчета коэффициента суммарной помехи и его стандартного отклонения.
Для этого вычисляем переходные коэффициенты αт и βт по формулам [3]:
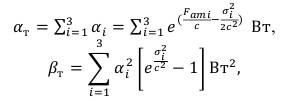
(44)
(45)
где σi=Dui/1,282 – стандартное отклонение коэффициента шума i-й помехи, рассчитываемое через значение верхней децили;
Fami – медианное значение коэффициента шума i-й помехи;
с=4,343 – коэффициент.
Вычисляем стандартное отклонение коэффициента шума суммарной помехи [3]
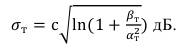
(46)
Вычисляем медианное значение коэффициента шума суммарной помехи по формуле [3]:
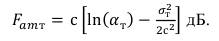
(47)
Вычисляем действующее значение коэффициента шума суммарной помехи
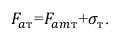
(48)
Медианное значение напряженности электрического поля суммарной помехи Etm в точке приема для эквивалентной антенны определяется по формуле (23) при подстановке в формулу Famт, затем по формуле (24) переводим в (мкВ/м). Аналогично по формулам (23) и (24) определяем среднеквадратическое отклонение напряженности поля суммарной помехи σЕt. По формуле (25) определяем коэффициенты пропорциональности k для суммарной помехи. Определяем действующее значение напряженности поля суммарной помехи Eпt в точке приема по формуле (26). Напряжение суммарной помехи на входе приемника при эквивалентной антенне определяется по формуле (27). Для реальной антенны напряжение суммарной помехи будет определяться по формуле (28). Медианное значение напряжения суммарной помехи и стандартное отклонение от медианного значения определяем по формулам (31) и (32). По формуле (33) и (34) находим отношение с/ш на входе приемника, подключенного к антеннам полуволновой и волновой симметричный вибраторы.
Напряжение суммарной помехи имеет огибающую, распределенную по полунормальному закону.
Примечания:
Полунормальное распределение – нормальное распределение с удвоенной плотностью вероятности, определенное на половине интервала.
Моделирование канала КВ радиосвязи
Особенности моделирования
Для моделирования канала КВ радиосвязи необходимо сформировать высокочастотный сигнал и помеху, действующие на вход радиоприемника.
Уровень высокочастотного сигнала может быть фиксированным и превышающим чувствительность приемника, уровень помехи при этом должен регулироваться и соответствовать расчетному отношению с/ш на входе приемника.
Как было показано выше, в КВ диапазоне нужно учитывать три основных типа помех: промышленные помехи с нормальным законом распределения, галактический шум с нормальным законом распределения, и атмосферные помехи с логнормальным законом распределения.
Для экономии материальных ресурсов есть смысл вместо трех помех формировать две, одну распределенную по нормальному закону, со среднеквадратическим отклонением, определяемым по формуле:
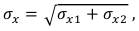
(49)
где σх1 и σх2 – среднеквадратические отклонения формируемых промышленной помехи и галактического шума, и вторую – атмосферную помеху с логнормальным распределением.
Имеются стандартные программы для формирования случайных величин с такими законами распределения.
Еще менее затратным является формирование одной суммарной помехи, распределенной по полунормальному закону.
При формировании помех возникают определенные сложности. По методике международного союза электросвязи [3], были определены параметры огибающей этих помех: медианное значение амплитуды огибающей mE и среднеквадратическое отклонение амплитуды огибающей от медианного значения σE. А для формирования помехи нужно знать математическое ожидание случайной величины и среднеквадратическое отклонение формируемой случайной величины х(t) от математического ожидания, обозначим его σх. Кроме того известно, что математическое ожидание помехи равно нулю.
Для формирования случайного процесса, соответствующего параметрам огибающей рассчитанной помехи, требуется найти связь между вычисленными выше параметрами огибающей помехи (медианным значением амплитуды огибающей mE и среднеквадратическим отклонение амплитуды огибающей от медианного значения σE), и параметрами формируемой случайной величины.
Следует рассмотреть формирование случайных величин с огибающими, распределенными по нормальному и логарифмически нормальному законам распределения.
Формирование случайной величины с огибающей, распределенной по нормальному закону.
Первый способ.
Рассмотрим формирование помехи с огибающей, распределенной по нормальному закону, путем формирования одной случайной величины, распределенной по нормальному закону. Функция распределения случайной величины, распределенной по нормальному закону, записывается в виде:
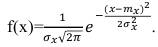
(50)
Определим параметры огибающей этой случайной величины. По аналогии с огибающей сигнала, под огибающей случайного процесса одной случайной величины будем понимать совокупность положительных значений случайного процесса, то есть значения х≥0. Тогда медианное значение огибающей будет определяться как математическое ожидание положительных значений случайного процесса по формуле:
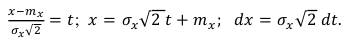
(51)
Произведем замену переменной:
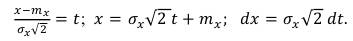
(52)
Тогда
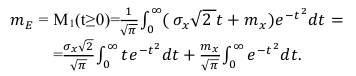
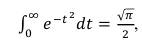
Учитывая, что получим

(53)
Дисперсию огибающей, определяем, как второй момент от положительных значений случайного процесса по формуле:

(54)
Произведя замену переменной, аналогичную (52), получим:
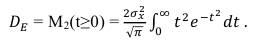
Произведя интегрирование по частям получим:
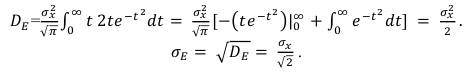
(55)
(56)
Если помеха, распределенная по нормальному закону, имеет математическое ожидание mx=0 и некоторое среднеквадратическое отклонение от математического ожидания σх, то медианное значение огибающей этого процесса, mE и среднеквадратическое отклонение от медианного значения σE, в соответствии с (44) и (47), всегда будут равны:
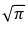
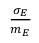
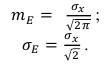
Для такого случайного процесса отношение всегда равно .
Поэтому, таким способом невозможно сформировать помеху с требуемыми параметрами огибающей.
Второй способ.
Рассмотрим формирование помехи посредством формирования двух случайных процессов, основного и сопряженного.
Итак, требуется сформировать некоторую случайную величину х(t), распределенную по нормальному закону с параметрами: математическое ожидание mx=0, среднеквадратическое отклонение σх, которое зависит от среднеквадратического отклонения огибающей. Определим параметры огибающей этой случайной величины посредством сопряженного процесса [1]. С помощью преобразования Гильберта можно найти некоторую случайную величину y(t), сопряженную с величиной x(t) [1]
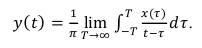
(57)
Тогда случайную величину x(t) и ей сопряженную y(t) можно представить в виде [1]:
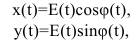
(58)
(59)
где
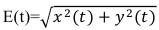
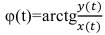
– фаза случайного процесса.
(61)
Математическое ожидание случайной величины y(t) my=0, а среднеквадратическое отклонение σy=σх.
Определим среднеквадратическое отклонение огибающей σЕ(t) случайного процесса и установим его связь со среднеквадратическим отклонением σх исходного случайного процесса.
В формуле (60) под знаком корня квадратного имеются две случайные величины, которые являются квадратичными функциями случайного процесса. Функция плотности вероятности для нормального закона имеет вид [4]:
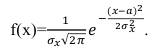
(62)
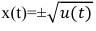
Функция плотности вероятности для нормального закона при квадратичной функции случайного процесса приведена в [1] и для
u
(
t
)=
x
2
(
t
) и, соответственно, будет иметь вид:
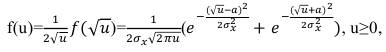
(63)
при a=0 функция будет иметь вид:
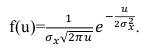
(64)
Математическое ожидание этой квадратичной функции mu вычислим как первый момент случайной величины:
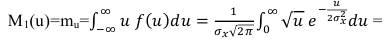
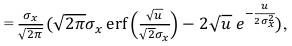
(65)
и после подстановки пределов получаем:
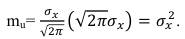
(66)
Тогда математическое ожидание огибающей случайного процесса, то есть функции E(t), будет определяться:
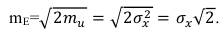
(67)
В данном случае математическое ожидание огибающей будет и ее медианным значением.
Дисперсию квадратичной функции Du вычислим как второй момент случайной величины:

(68)
и после подстановки пределов получаем:
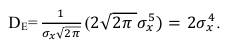
(69)
Тогда среднеквадратическое отклонение квадратичной функции будет равно:
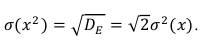
(70)
Дисперсия огибающей случайного процесса, то есть функции E(t), будет определяться:
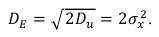
(71)
Среднеквадратическое отклонение огибающей случайного процесса от медианного значения будет вычисляться по формуле:
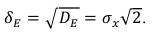
(72)
Обратим внимание на то, что для случайной величины, распределенной по нормальному закону с математическим ожиданием mx=0, параметры огибающей вычисляются по одной и той же формуле:
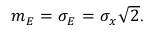
Это означает, что в шуме, моделируемом посредством основного и сопряженного процесса, формула (57), соотношение
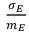
Третий способ.
Рассмотрим еще один способ формирования помехи посредством формирования двух процессов: процесса, соответствующего среднеквадратическому отклонению от медианного значения огибающей, и процесса, соответствующего медианному значению огибающей.
Для этого сформируем случайные величины x(t) огибающей случайного процесса X(t), распределенные по нормальному закону с параметрами: mx=0 и σx. Сформируем случайные величины y(t) случайного процесса Y(t), распределенного по равномерному закону в котором случайная величина может принимать только два значения: y(t)=± my. Вычислим случайные величины z(t)=x(t)+y(t), генерируемого процесса Z(t). Для формирования случайных величин x(t) в MATLAB можно сгенерировать случайную величину x1=rand, распределенную по равномерному закону в диапазоне [0,1], а затем по интегральной функции нормального закона распределения получить случайные величины x(t).
Для формирования случайных величин y(t) в MATLAB можно сгенерировать случайную величину y1=randi([0,1],1), распределенную по равномерному закону и имеющую значения только 0 и 1, а затем сформировать случайную величину y(t) по следующему закону:
y= my при y1=1;
y= -my при y1=0,
или наоборот, это значения не имеет.
Рассмотрим формируемую таким способом помеху. Плотность распределения формируемой случайной величины x(t), распределенной по нормальному закону, запишется в виде [4]:
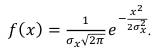
(73)
Случайная величина y(t) распределена по равномерному закону и имеет всего два значения +my и –my, вероятность появления которых Р=1/2.
Суммарная случайная величина z(t)=x(t)+y(t)=x(t)±my, определена на двух интервалах: z≥0 и z≤0. При z≥0 случайная величина распределена по нормальному закону с параметрами σx и плюс my, а при z≤0 с параметрами σx и минус my. С учетом вероятности появления положительных и отрицательных значений случайной величины ее плотность распределения можно записать в виде:

(74)
(75)
Определим медианное значение огибающей этого случайного процесса в соответствии с (51).
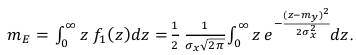
Подставив медианное значение, вычисленное в (53) для нормального закона распределения получим:
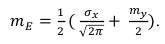
(76)
Определим дисперсию огибающей этого случайного процесса в соответствии с (54).
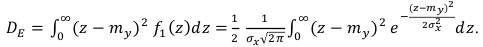
Подставив значение дисперсии огибающей, вычисленное в (55) для нормального закона распределения получим:
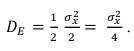
Соответственно
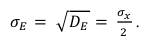
(77)
Из (76) и (77) найдем значения параметров σx и my, необходимых для формирования случайного процесса с огибающей, соответствующей рассчитанной.
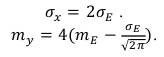
(78)
(79)
Задача решена. С помощью данного способа имеется возможность формировать случайный процесс с параметрами огибающей, соответствующими требуемым.
Формирование случайной величины с огибающей, распределенной по логарифмически нормальному закону.
Если случайная величина x(t) распределена по логарифмически нормальному закону, то ее плотность вероятности запишется в виде [4]:

(80)
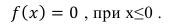
Тогда случайная величина
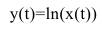
(81)
будет распределена по нормальному закону с плотностью распределения [4]
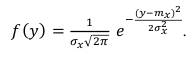
(82)
Как видно из (70) и (71), при переходе от одного закона распределения к другому параметры mx и σx не изменяются, поэтому и параметры случайной величины с огибающей, распределенной по нормальному закону, mE и σE не будут изменяться при переходе к огибающей, распределенной по логарифмически нормальному закону. Из (71) находим формулу для перехода от случайной величины, распределенной по нормальному закону, к случайной величине, распределенной по логарифмически нормальному закону
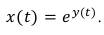
(83)
Способ формирования случайной величины z(t) с огибающей, распределенной по нормальному закону бы определен выше в третьем способе. Остается по формуле, аналогичной (83), от случайной величины z(t) перейти к случайной величине z1(t) с огибающей, распределенной по логарифмически нормальному закону
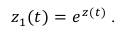
(84)
Таким образом, способ формирования случайной величины с огибающей, распределенной по логарифмически нормальному закону, также определен.
Формирование случайной величины с огибающей, распределенной по полунормальному закону.
Под полунормальным законом распределения (Half-normal distribution) понимают нормальный закон распределения, заданный на половине интервала, но для которого площадь под кривой спектральной плотности равна площади под кривой спектральной плоскости нормального закона распределения, заданного на всем интервале от -∞ до +∞. В литературе на русском языке упоминание об этом законе распределения встречается крайне редко, в основном под названием «усеченный слева нормальный закон распределения».
Плотность распределения и интегральная функция для полунормального закона распределения записывается в виде [5]:
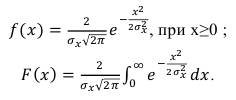
(85)
(86)
Из формулы (85) видно, что это центрированный (mx=0) нормальный закон распределения с удвоенной плотностью, заданный на половине интервала.
Определяя по формулам (51) и (54) медианное значение огибающей этого закона распределения и стандартное отклонение от медианного значения получаем:
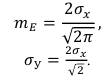
(87)
(88)
Сравнивая с аналогичными параметрами, полученными для нормального закона в (53) и (56), видим, что для полунормального закона распределения эти параметры в два раза больше, чем для нормального закона.
Формировать случайную величину с огибающей, распределенной по полунормальному закону будем аналогично рассмотренному выше третьему способу формирования случайной величины, но с учетом значений, полученных в формулах (87) и (88). Медианное значение огибающей и стандартное отклонение от огибающей должны бать в 2 раза больше, чем для огибающей, распределенной по нормальному закону, полученные в (76) и (77), в результате чего будем иметь:
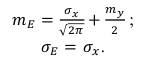
(89)
(90)
Откуда получаем параметры для формирования случайной величины с огибающей, распределенной по полунормальному закону:
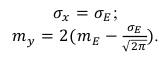
Заключение
Для моделирования радиоканала, сформированные таким образом с помощью ПЭВМ сигнал и помехи следует подать на вход радиоприемного устройства или его имитатора, при этом отношение с/ш на входе радиоприемного устройства для каждого вида помехи должно соответствовать вычисленному значению.
Программа расчета параметров для моделирования КВ радиоканала KVkanal приведена в приложении А, инструкция по работе с программой KVkanal приведена в приложении Б.
Литература
Левин Б.Р. Теоретические основы статистической радиотехники. Издательство «Советское радио», М-1969.
Надененко С.И. Антенны Государственное издательство литературы по вопросам связи и радио, М-1959.
Рекомендация МСЭ-R Р.372-9 Радиошум, 2007.
Вентцель Е.С. Теория вероятностей. Издательство «Наука», М-1969.
Википедия (на английском языке), Half-normal distribution.
Приложение А
Программа
KVkanal
(Расчет параметров для моделирования КВ радиоканала)
Исходный код программы
clc; clear; close all;
% расчет отношения сигнал/шум на входе приемника в КВ диапазоне










