Макрокинетика сушки

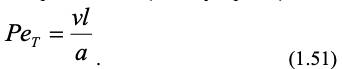
Он аналогичен по форме критерию Рейнольдса, который может быть рассмотрен как отношение скоростей переноса количества движения конвективного и молекулярного.

Поскольку на конвективный теплоперенос влияют условия движения среды и описывающие его дифференциальные уравнения решаются совместно с уравнениями движения потока, в критериальную зависимость, описывающую теплоперенос, должны входить и критерии гидродинамического подобия. Это критерии. Но, Fr, Re и Г. Критерий Эйлера обычно не входит в эту зависимость, т. к. не является определяющим для теплопереноса.

Так как в критерии Fr и Re входит скорость, используется их комбинация – критерий Галилея, не содержащий скорости:

или критерий Архимеда, включающий отношение плотности одной среды и разности плотностей двух сред:

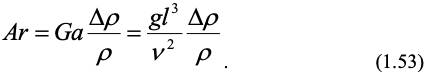
Если разность плотностей вызвана термическим расширением среды (T – коэффициент термического расширения), то:

,

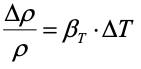
где Т – абсолютная температура.

После подстановки этого соотношения в критерий Архимеда получим критерий Грасгофа:

Для газов

,

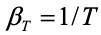
тогда критерий Грасгофа примет вид:

При сочетании критерия Рет с критерием Re получим критерий Прандтля, характеризующий теплофизические свойства среды или соотношение полей скоростей и температур:

Если граничным условием теплопереноса является линейность теплового потока – уравнение (1.23) тогда в сочетании с уравнением (1.29) получим:

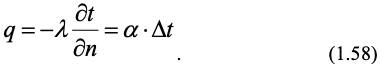
Из этого соотношения, переходя к размерным величинам, получим критерий Нуссельта, характеризующий подобие граничных условий:

Критерий Нуссельта рассматривают также как безразмерный коэффициент теплопереноса, поэтому он является определяющим. С учетом рассмотренных критериев перенос тепла можно рассматривать в виде следующей критериальной зависимости:

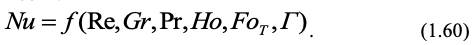
Для стационарного теплопереноса из зависимости (1.60) исключаются критерии. Но и Foт, содержащие время.

Критерий Nu является наиболее удобной величиной для расчета молекулярного переноса или переноса в ламинарном движении [10]. В случае развитой турбулентности более удобным оказывается использование критерия Стентона:

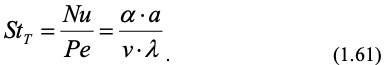
Тогда в зависимости (1.61) определяющим критерием вместо Nu будет критерий Stт.

Массоперенос. Критерии массопереноса и общая критериальная зависимость выводятся аналогично теплопереносу. Для этого рассмотрим подобное преобразование дифференциального уравнения массопереноса (1.22). Для одномерного потока, когда С = f (x, τ) в отсутствии источников для объекта моделирования запишем (индексы опущены):

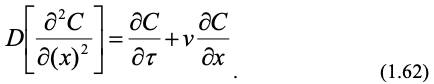
Аналогичное уравнение с учетом констант подобия запишем для модели:

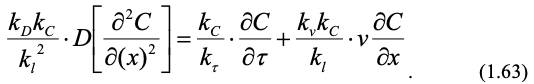
Чтобы уравнения (1.62) и (1.63) были идентичны, все множители из констант подобия должны быть равны, тогда:

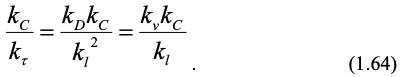
Из первого равенства выражения (1.64), подставив значения констант подобия, получим безразмерный комплекс – диффузионный критерий Фурье, который характеризует изменение молекулярного массопереноса во времени

Из второго равенства выражения (1.64), подставив значения констант подобия, получим другой безразмерный комплекс – диффузионный критерий Пекле, который представляет собой отношение массопереноса за счет движения среды (конвективный) и за счет молекулярной диффузии (молекулярный)

Он аналогичен по форме критерию Рейнольдса, и тепловому критерию Пекле.

Поскольку на конвективный массоперенос влияют условия движения среды и описывающие его дифференциальные уравнения решаются совместно с уравнениями движения потока, в критериальную зависимость, описывающую массоперенос, должны входить и критерии гидродинамического подобия. Это критерии. Но, Fr, Re и Г. Критерий Эйлера не входит в эту зависимость, т. к. не является определяющим для массопереноса.

При сочетании критерия Ре с критерием Re получим критерий Шмидта (в отечественной литературе его часто называют диффузионным критерием Прандтля), характеризующий соотношение молекулярного переноса количества движения и молекулярной диффузии или соотношение полей скоростей и концентраций:

Если граничным условием массопереноса является линейность потока вещества – уравнение (1.18), тогда в соответствии с уравнением (1.32) получим равенство:

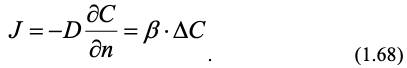
Из этого соотношения, переходя к размерным величинам, получим критерий Шервуда (в отечественной литературе его часто называют диффузионным критерием Нуссельта), характеризующий подобие граничных условий при массопереносе:

Критерий Шервуда рассматривают также как безразмерный коэффициент массопереноса, поэтому он является определяющим. С учетом рассмотренных критериев перенос вещества можно рассматривать в виде следующей критериальной зависимости:

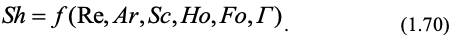
Для стационарного массопереноса из зависимости (1.70) исключаются критерии. Но и Fo, содержащие время.

Критерий Sh является наиболее удобной величиной для расчета молекулярного переноса или переноса в ламинарном движении [6]. В случае развитой турбулентности более удобным оказывается использование диффузионного критерия Стентона, т. к. он в этом случае близок к постоянному значению

Тогда в зависимости (1.70) определяющим критерием вместо критерия Sh будет критерий St. Общий вид зависимости при этом сохранится.

1.12 Внешняя и внутренняя задачи

Все процессы переноса количества движения, массы и тепла можно рассматривать в условиях внешней и внутренней задач.

Внешней задачей рассматриваются процессы переноса при обтекании тела потоком, причем размеры потока можно считать бесконечно большими. Роль линейного размера l при этом будет играть размер обтекаемого тела.

Примером внешней задачи при переносе количества движения является движение тела в бесконечной среде. Примером внешней задачи при теплопереносе является внешний теплообмен при обтекании средой горячей трубы. Примером внешней задачи при массопереносе является растворение кристалла при обтекании его потоком жидкости.

Внутренней задачей рассматриваются процессы переноса внутри твердого тела или внутри трубы, аппарата, канала. Роль линейного размера l при этом будет играть внутренний размер тела, трубы, аппарата или канала.

Примером внутренней задачи при переносе количества движения является движение среды (газ, жидкость) в трубе. Примером внутренней задачи при теплопереносе является теплопроводность внутри пластины при ее нагревании или охлаждении. Примером внутренней задачи при массопереносе является изменение влажности пористого материала при обтекании его (сушке) потоком горячего воздуха.

Необходимо отметить, что поскольку условия переноса (граничные условия) во внешней и внутренней задачах различны, решения дифференциальных уравнений и значения критериев для этих задач также будут различными. Так, например, при движении шара в сплошной среде ламинарный режим сохраняется до значения критерия Рейнольдса равном 2, а при движении среды в трубах – до значения 2100 – 2300.

Следует отметить, что явления переноса часто протекают одновременно во внешней и внутренней задаче и очень важно определить, какая из них в наибольшей степени определяет перенос (лимитирует). Примером совместной внешней и внутренней задач при переносе количества движения является движение капли, пузырька в сплошной среде. Внешняя задача – обтекание объекта потоком, а внутренняя задача – циркуляция жидкости (газа) внутри капли (пузырька). Следует отметить, что внутренняя циркуляция может значительно снизить скорость движения тела. Если влияние внешней и внутренней задач при переносе количества движения одного порядка, то говорят о смешанной задаче.

Примером совместной внешней и внутренней задач при теплопереносе является теплопередача через стенку (Рис. 1.5). Здесь внешняя задача – конвективный теплоперенос от среды к стенке, а внутренняя – теплопроводность внутри стенки. Если лимитирует теплопроводность (материал стенки теплоизолирующий), то коэффициент теплопередачи по уравнению (1.31). К , т. е. конвективными сопротивлениями можно пренебречь. Теплопередачу в условиях совместной внешней и внутренней задач характеризует тепловой критерий Био (аналог критерия Нуссельта)

Если в критерии Нуссельта оба параметра α и относятся к одной среде, то в критерии Био α – определяет конвективный теплообмен от среды к стенке (или наоборот) – внешняя задача, а параметр / l – определяет теплопроводность стенки – внутренняя задача. Если Biт 0, то лимитирует внешняя задача, если Biт → ∞, то лимитирует внутренняя задача. Если влияние внешней и внутренней задач при теплопередаче одного порядка, то говорят о смешанной задаче передачи тепла.

Примером совместной внешней и внутренней задач при массопереносе является процесс конвективной сушки пористого материала. Изменение влажности пористого материала происходит при его сушке потоком горячего воздуха. Здесь внешняя задача – конвективный массоперенос от среды к материалу, а внутренняя – перенос влаги (массопроводность) внутри материала. Перенос влаги внутри материала может быть учтен коэффициентом диффузии D внутри материала. Если лимитирует массоопроводность, то процесс массопередачи определяет диффузия внутри материала, т. е. конвективным массопереносом можно пренебречь. Массопередачу в условиях совместной внешней и внутренней задач характеризует диффузионный критерий Био (аналог критерия Шервуда)

Однако, если в критерии Шервуда оба параметра и D относятся к одной среде, то в критерии Био – определяет конвективный массооперенос от материала к среде (или наоборот при сорбции) – внешняя задача, а параметр D / l – определяет массопроводность материала – внутренняя задача. Если Bi → 0 (практически при Bi 0,2), то лимитирует внешняя задача, если Bi → ∞ (практически при Bi 50), то лимитирует внутренняя задача. Если значения критерия Био лежат в интервале от 0,2 до 50, то имеет место смешанная задача и влияние обеих внешней и внутренней задач существенно, одного порядка [10].

1.13 Критериальные зависимости стационарного переноса

Перенос количества движения. Рассмотрим примеры стационарного переноса количества движения. Внутренней задачей гидродинамики является описание движения жидкостей и газов в трубах. Для стационарного горизонтального движения в трубах (отсутствуют критерии Фруда и гомохронности) критериальную зависимость (1.46) записывают в виде

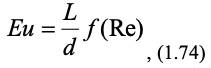
где геометрический критерий представляет собой отношение длины L к диаметру d трубы. Функциональную зависимость критерия Рейнольдса называют коэффициентом гидравлического сопротивления в трубах и обозначают

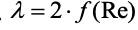
Подставив выражение критерия Эйлера в (1.74), получим уравнение Дарси:

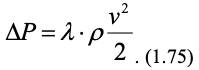
Можно показать [6], что в ламинарном режиме (Re 2100):

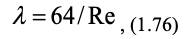
а в развитом турбулентном режиме для гладких труб (Re 10000) применяется зависимость Блазиуса:

Для шероховатых труб (Δ – высота выступов шероховатости) и переходного режима [6] используют зависимости общего вида:

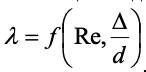
Примером внешней задачи переноса количества движения является стационарное движение сферических частиц в сплошной среде. В критериальной зависимости (1.46) в этом случае отсутствуют критерии Фруда, гомохронности и геометрический, т. к. сферическая частица имеет только один линейный размер – диаметр. Эта зависимость примет вид:

Равномерное движение частиц обусловлено равновесием сил, действующих на частицу – тяжести, архимедовой и сопротивления среды [6]:

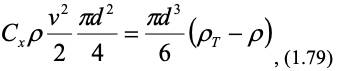
где Сх – коэффициент лобового сопротивления частицы.

С учетом, что потери давления при обтекании частицы равны отношению силы сопротивления к сечению частицы

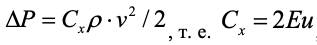
получим из (1.79):

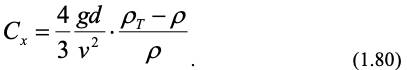
Таким образом, движение частицы сводится к зависимости коэффициента лобового сопротивления Сх от числа Рейнольдса. В ламинарном режиме (Re 2) движение частицы описывается законом Стокса

,

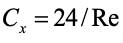
в переходном (2 Re 500), –

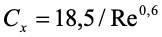
а в турбулентном (500 Re 2105) Сх практически не зависит от Re и составляет Сх = 0,44.

Теплоперенос. Рассмотрим примеры описания стационарного теплопереноса в трубах и каналах (внутренняя задача) критериальными уравнениями. В этом случае общая критериальная зависимость (1.60), в пренебрежении влиянием силы тяжести, записывают в следующем виде (отсутствуют критерии Грасгофа, Фурье и гомохронности):

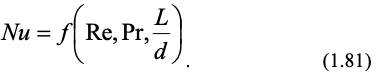
Конкретный вид зависимости (1.81) для ламинарного режима найден Левеком [10]:

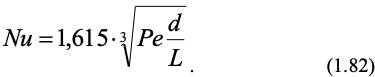
Для труб большой длины в установившемся ламинарном режиме, при (Реd/L) 20 величина Nu стремится к постоянному значению 3,695 теоретически полученному Нуссельтом.

Для турбулентного течения в трубах (Re 10000) при отношении L/d 50 в литературе используется уравнение:

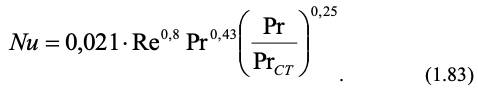
Для газов последний множитель в уравнении (1.83) равен единице и Pr зависит только от атомности газа. Так для воздуха в этом случае получим:

Для стационарного теплопереноса при обтекании тел (внешняя задача) вид зависимости (1.83) сохраняется. Так при перпендикулярном обтекании коридорных и шахматных пучков труб при Re 1000 используется уравнение:

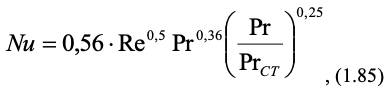
а для обтекания шахматных пучков труб при Re 1000 применяется уравнение:

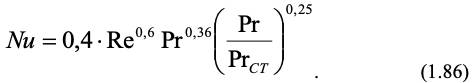
Для газов последний множитель в уравнении (1.86) равен единице и Pr зависит только от атомности газа. Для воздуха в этом случае получим:

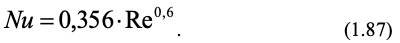
Массоперенос. Рассмотрим примеры описания стационарного массопереноса критериальными уравнениями. В этом случае, в пренебрежении влиянием силы тяжести, общая критериальная зависимость (1.70) записывается в следующем виде (отсутствуют критерии Архимеда, Фурье и гомохронности)

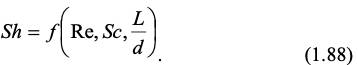
Конкретный вид зависимости (1.88), например, для адсорбции на насыпном активированном угле с размером частиц 1,7-2,2 мм при средней скорости потока 0,3-2 м/с имеет вид

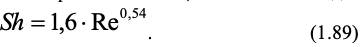
Аналогичный вид зависимости с близкими численными значениями коэффициентов приведен [6] для адсорбции в кипящем слое активированным углем паров четыреххлористого углерода.

Если одновременно имеет место тепло- и массоперенос (например, при сушке твердых материалов), то для расчета процесса необходимо использовать критериальные уравнения для тепло- и массопереноса.

1.14 Сушка как процесс тепломассопереноса

Сушка (обезвоживание) – это процесс удаления путем испарения влаги при нагревании высушиваемого материала и отвод образующихся паров. Таким образом, при сушке происходит тепло- и массоперенос. Сушка является в значительной степени более энергоемким процессом, по сравнению с другими видами обработки материалов. Применение неправильно выбранных режимов или конструкций аппаратов при сушке того или иного материала приводит к удорожанию и выпуску конечного продукта неудовлетворительного качества. Поэтому важно математическое описание этого процесса и выбор наиболее рациональной конструкции сушилки, а также выполнение точного расчета всех параметров сушки и последующее строгое соблюдение режима сушки на действующем сушильном оборудовании.

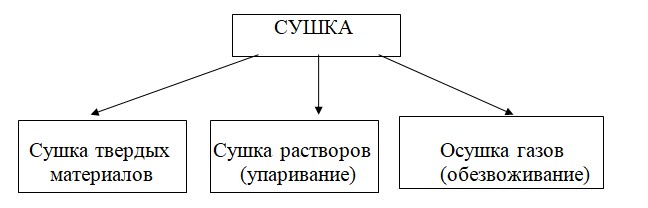
Рис. 1.7 Виды сушки материалов различного агрегатного состояния.

Процессу сушки могут быть подвергнуты твердые материалы, растворы (путем выпаривания) и газы (осушка газов). Схематично классификация видов сушки представлена на Рис. 1.7. Наиболее часто используется и поэтому более подробно рассматривается в данной монографии сушка твердых материалов.

Подвергаемые сушке материалы поступают в сушильные установки часто после предварительного удаления влаги, а иногда и минуя эту стадию. Начальная влажность материала, в целях экономии энергозатрат на сушку, должна быть возможно более низкой. Чем она ниже, тем меньшее количество воды потребуется удалить в процессе сушки. Поэтому перед сушкой избыточную воду из материала по возможности удаляют.

Влага из материалов может быть удалена различными способами: 1) механическим: 2) физико-химическим; 3) собственно сушкой.

При механическом удалении влага отжимается механически: путем отжима, прессования, фильтрования или центрифугирования (под действием центробежной силы в центрифугах). Механическое обезвоживание применяется для материалов, допускающих деформацию (ткани, войлок, волокнистые материалы, торф и т. п.). В текстильной, пищевой промышленности и производствах химических волокон, например, для этой цели используются фильтр-прессы, вакуум-фильтры и центрифуги. Механически удаляется только часть влаги, содержащейся в материале. После механического удаления обычно применяется дополнительная обработка влагоудаления из материала (тепловая и др. виды сушки).

Физико-химические способы сушки основаны на применении водоотнимающих средств. Эти способы не получили применения в производстве, но применяются в лабораторной технике (обезвоживание над серной кислотой, над хлористым кальцием в эксикаторах, силикагелем).

На Рис. 1.8 показаны разные способы удаления влаги из материалов с их детализацией: механический способ удаления влаги, физико-химический и удаление влаги способом сушки. Обычно при сушке из материала удаляется поверхностная влага в начале процесса, а затем и внутренняя. В ряде производственных процессов из материала могут удаляться и органические растворители (ацетон, бензин и др.), например, в производствах химических волокон при сухом и мокром формовании, в производстве искусственной кожи, нефтепереработке. Многие виды сушилок и методы их расчета могут быть использованы как для удаления влаги, так и для процессов удаления органических растворителей.

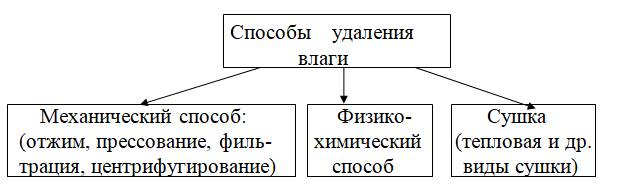
Рис. 1.8 Способы удаления влаги из материалов.

Коэффициент массоотдачи при сушке плоских материалов для периода с постоянной скоростью процесса может быть определен из следующего критериального уравнения:

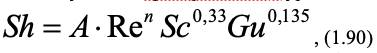
где определяющим размером при вычислении критериев Sh и Re является длина поверхности испарения в направлении движения сушильного агента. В уравнение (1.90) входит параметрический критерий Гухмана:

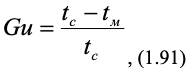
где tc и tм – температуры сухого и мокрого термометров.

Величины коэффициентов А и n в уравнении (1.90) зависят от режима движения сушильного агента, определяемого критерием Рейнольдса. Эта зависимость в форме таблицы представлена ниже.

Таблица 1.1 Коэффициенты критериального уравнения сушки

При тепломассопереносе в процессе сушки уравнения тепло- и массопереноса взаимосвязаны. Поток тепла q, подводимый для удаления влаги из материала, может быть найден как произведение потока массы удаляемой влаги J на теплоту парообразования r:

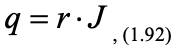
или с учетом уравнений (1.29) и (1.32):

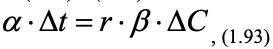
В периоде постоянной скорости сушки скорость сушки с поверхности материала F, с учетом соотношения (1.93) может быть найдена как:

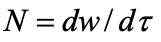
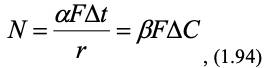
где Δt – разность температуры греющего агента и температуры поверхности материала, ΔС – разность концентраций влаги у поверхности материала и в потоке сушильного агента (вместо разности концентраций часто берут разность давлений водяного пара у поверхности материала и парциального давления водяного пара сушильного агента).

При конвективной сушке температура поверхности материала близка к температуре мокрого термометра. При кондуктивной сушке температура поверхности материала близка к температуре кипения жидкости. При других способах сушки и при комбинированной сушке температура поверхности материала находится между этими значениями температур.

Как следует из уравнения (1.94), скорость сушки в первом периоде можно определить как из уравнения тепло-, так и из уравнения массопереноса. Коэффициенты α и находят из соответствующих критериальных уравнений.

Предваряя рассмотрение макрокинетики конкретных процессов сушки, рассмотрим сначала свойства применяемых теплоносителей (сушильных агентов) и свойства высушиваемых материалов, как объектов участвующих при обработке материалов в процессе сушки.

Глава II

Типы и свойства тепло- и влагоносителей

Теплоносителем является агент, подводящий тепло необходимое для сушки. Теплоносителями в промышленных сушильных установках служат, как правило, воздух, водяной пар или топочные газы. В лабораторных и сушильных установках малой производительности иногда используют электрический обогрев с использованием тока как промышленной, так и высокой частоты (микроволновая сушка), а также радиационный нагрев высушиваемого материала с применением излучателей разного типа. На Рис. 2.1 приведена классификация сушилок по типу используемого теплоносителя (способу подвода тепла).