Расчеты в Excel

……..

Запись программы в Exрcel

Первым делом откроем лист Excel по имени Е_00. ( Скачать из приложения ).

Сохраним его как Е 10. Далее на листе необходимо выполнить заголовок расчета:

«Линия на плоскости». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 10. Затем сохраняем как Е 10_Z.

Проверим форматирование столбиков и защитим лист @007.

Примечание: Если Запись программы в Exрcel. такая краткая – значит ничего нового в программировании

этой программы ( листа ) нет. Если нужны подробности – скачайте по ссылке приложение. В приложении

есть открытые и закрытые листы. Открытые листы для рассмотрения подробностей. Закрытые листы –

для практических расчетов.

Расчет линейной интерполяции

Линейная интерполяция применяется при работе с табличными данными.

Из таблицы имеем две взаимосвязанных пары значений какой то функции.

Необходимо вычислить ординату при значении абсциссы близком взятой из таблицы пары абсцисс.

Например: Абсцисса x1 = 10; Ордината y1 = 20;

Абсцисса x2 = 90; Ордината y2 = 180;

Необходимо вычислить Ординату Yx при Абсциссе Хх = 50;

Примечание: Абсцисса Хх может также быть немного больше

или меньше крайних значений известных табличных Абсцисс.

Рис. Линейная интерполяция.

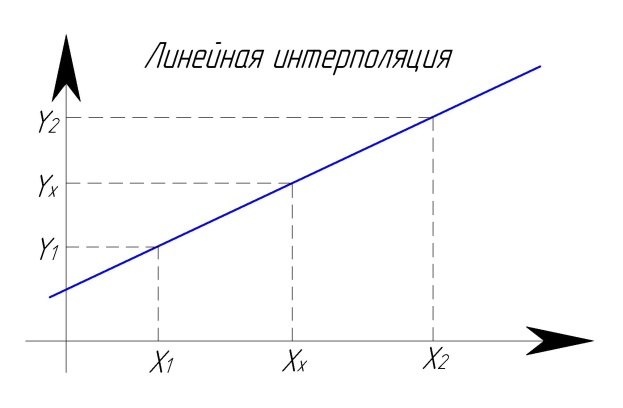
Расчет: RF-01.

Yy = (((y2-y1)*(Хx-x1)) / (x2-x1))+y1; Yy = (((180-20)*(50-10)) / (90-10))+20;..

Yy = ( 6400 / 80 )+20; Yy = 100;..

,,,,

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_10. ( Скачать из приложения ).

Сохраним его как Е 11. Далее на листе необходимо выполнить заголовок расчета:

«Линейная интерполяция». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 11. Затем сохраняем как Е 11_Z.

Проверим форматирование столбиков и защитим лист @007.

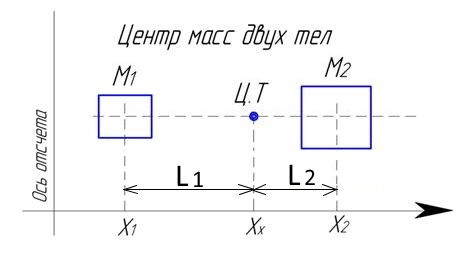
Расчет центра масс

Исходные данные:

Масса первого тела М1 = 6;

Масса второго тела М2 = 8;

От оси до центра массы первого тела Х1 = 4;

От оси до центра массы второго тела Х2 = 14;

Рис. Центр масс.

…

….

Расчет:

От оси до центра массы системы двух тел:

Рассчитываем как моменты масс относительно Оси отсчета Хх.

(L1+L2)=( X2-X1)= 10.. L1=(L1+L2)/((M1/M2)+1); L1=10/((6/8)+1).. ;

L1 = 5,7142857 … L2=4,285714..

Суммарная масса системы двух тел:

M=m1+m2; M= 6 + 8;.. M= 14 …

Проверка: М1*L1=M2*L2… 6*5,7142857=8*4,285714.. Равенство соблюдается..

( M1+M2)*(X1+L1)=(M1*X1)+(M2*X2).. (6+8)*(4+5,7142857)=(6*4)+(8*14)..

Равенство моментов соблюдается..

,,,,

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_10. ( Скачать из приложения ).

Сохраним его как Е 12. Далее на листе необходимо выполнить заголовок расчета:

«Центр масс двух тел». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 12. Затем сохраняем как Е 12_Z.

Проверим форматирование столбиков и защитим лист @007.

Расчет геометрии многогранника

Многогранник:

Описанный диаметр d.

Вписанный диаметр dv.

Ширина грани L.

Угол между вершинами U.

Исходные данные:

Описанный диаметр d = 100…

Вписанный диаметр dv = 80,90169943749474.

Число граней многогранника n = 5…

Рис. Пятигранник.

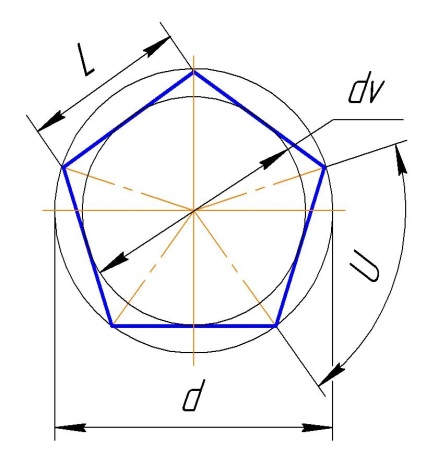
Расчет:

Половина угла на грань:

Ur = 180 / n; Ur = 180 / 5; Ur = 36…

Расчет при известном описанном диаметре.

Радиус описанного диаметра:

R=d / 2; R=100 / 2; R= 50…

Радиус вписанной окружности:

Rv=(d/2)*cos( Ur ); Rv= 50 * cos( 36 );

Rv= 40,45084972…

Вписанный диаметр:

.dv=Rv+Rv; .dv= 40,45084972 + 40,45084972;

.dv= 80,90169944…

Максимальный размер между вершинами:

X = d * ( cos ( 90 / n ))…

Ширина грани:

Sg= 2*(sqrt( R * R – Rv * Rv )); Sg= 2*(sqrt( 50 * 50 – 40,45084972 * 40,45084972 ));

Sg= 58,77852523…

Площадь многогранника:

S= ( Sg * Rv * n ) / 2; S= ( 58,77852523 * 40,45084972 * 5 ) / 2; S= 5944,103227…

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 13. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия многогранника». Далее форматируем столбики как описано @002. @003. @004. @004А.

Расчеты: Здесь много расчетов связанных с углами. Компьютер угловые функции ведет в радианах.

@010. Угол 180 градусов равен числу Pii = 3,1415926 радиан..

Перевод из градусов в радианы: Радианы = Градусы*Pii/180…

Перевод из радиан в градусы: Градус = Радиан*180/Pii…

Любая тригонометрическая функция требует ввода аргумента в радианах.

Аргумент следует предварительно рассчитать и в функцию вставить адрес ячейки с аргументом.

Формулы приведены выше и в Excel. Можно посмотреть в открытом листе Е13.

Выполняем защиту столбиков и сохраняем лист как Е 13. Затем сохраняем как Е 13_Z.

Проверим форматирование столбиков и защитим лист @007.

Геометрия коробовой кривой ( овала )

Коробовая кривая – этой кривой можно с достаточной точностью заменить овальную кривую.

К примеру с помощью программы расчета геометрии коробовой кривой можно рассчитать геометрические размеры обжатого уплотнительного круглого резинового кольца.

Рис. Коробовая построение.

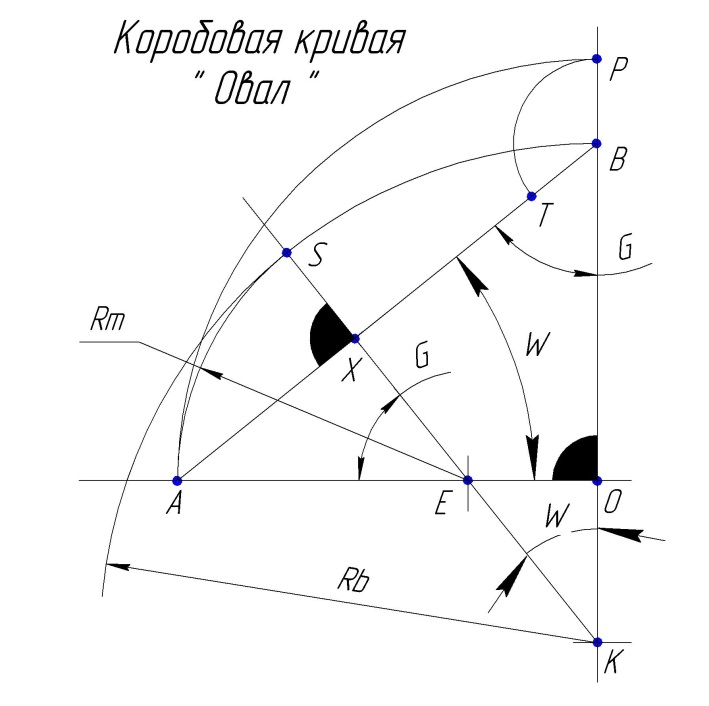
Построение:

Задано:

Большая полуось ОА… ОА = ОP..

Малая полуось ОВ.

Алгоритм Расчета:

ОА = ОP.. Построением..

Построением: РВ = ОА – ОВ; ТВ = РВ..

АВ =sqrt( АО*АО + ОВ*ОВ ); АТ = АВ – ТВ; ХТ = АТ / 2;

Из подобия треугольников: АХ / АО = АE / АВ; отсюда:

АE = АХ*АВ / АО; аналогично: ВК = ( АХ + ВТ )* АВ / ВО;

ОE = ОА – АE; ОК = ВК – ОВ; ХВ = ХТ + ТВ = AX + BT;

Rm=(XT*AB)/OA.. Малый радиус..

Rb=BK=(AB*(XT+PB))/OB… Большой радиус..

X=OB/OA..

UA=ATan(X).. Угол большого круга..

UB=(Pii/2)-UA… Угол малого круга..

SB=Pii*BK*BK.. Площадь круга с больш.R..

SM=Pii*Rm*Rm.. Площадь круга с малым .R..

SBS=SB*2*UA/Pii..

SMS=SM*2*UB/Pii..

KO=BK-OB..

OO1=OA-Rm..

STR=2*KO*OO1..

SO=(SMS+SBS)-STR..

XU=UA*360/Pii..

X=4*SO/Pii..

DS= sqrt(X)..

Для расчета площади сечения коробовой кривой :

Большой радиус Rb = КВ; Зная стороны ВК и ХВ – находим угол сектора «W».

Зная радиус Rb и угол сектора «W»– найдем площадь сектора.

Зная стороны ОК и ОE прямоугольного треугольника – найдем его площадь

и вычтем из площади сектора радиуса Rb.

Малый радиус Rm = EА; Зная угол «W»прямоугольного треугольника КХВ

определяем угол сектора малого радиуса как:

G = 90 – W; Далее: определим площадь сектора малого радиуса.

Площадь сечения коробовой кривой найдена.

Найдем диаметр круга равный по площади заданной коробовой кривой:

.d =sqrt( 4*S / Pii ); Где S – площадь заданной коробовой кривой.

Контрольный расчет:

Дано:

Большая ось = 80; Малая ось = 60;

Рис. Коробовая радиусы.

….

….

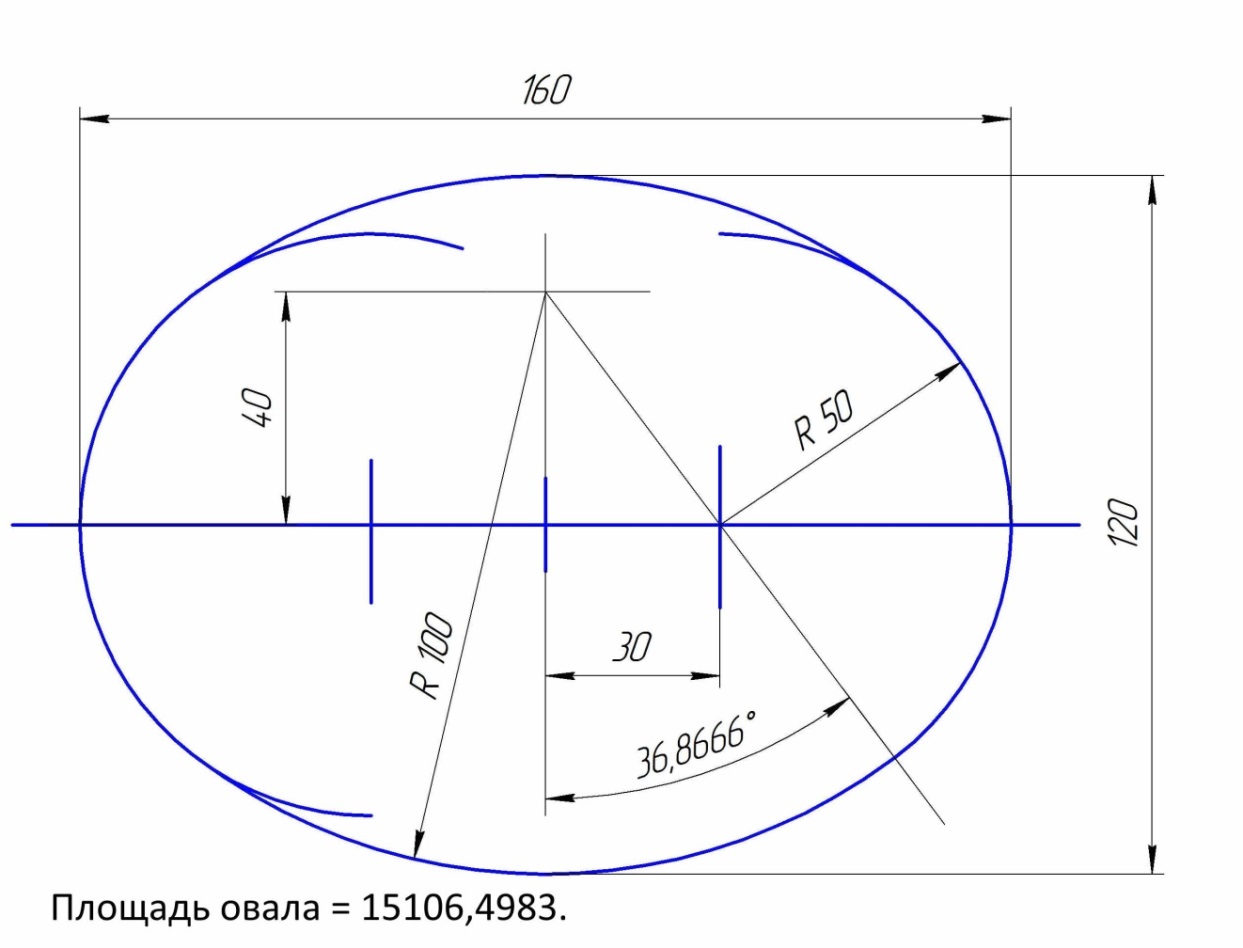
Расчет:

Больший радиус = 100,0..

От оси до центра Б. радиуса = 40,0..

Меньший радиус = 50,0..

От оси до центра M. радиуса = 30,0..

Угол раствора Б. радиусов = 73,739795..

Площадь ограниченная коробовой кривой = 15106,498;

Диам. Круга равной площади = 138,687;

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 14. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия овала». Далее форматируем столбики как описано @002. @003. @004. @004А.

Расчеты: Здесь много расчетов связанных с углами. Компьютер угловые функции ведет в радианах.

@010. Угол 180 градусов равен числу Pii = 3,1415926 радиан..

Перевод из градусов в радианы: Радианы = Градусы*Pii/180…

Перевод из радиан в градусы: Градус = Радиан*180/Pii…

Любая тригонометрическая функция требует ввода аргумента в радианах.

Аргумент следует предварительно рассчитать и в функцию вставить адрес ячейки с аргументом.

Формулы приведены выше и в Excel. Можно посмотреть в открытом листе Е14.

Все расчеты проведены в столбике «F»так как много промежеточных расчетов.

Итоговые результаты выведены в столбик результатов «D».

Рисунок вставляем в лист, как описано в @013.

Выполняем защиту столбиков и сохраняем лист как Е 14. Затем сохраняем как Е 14_Z.

Проверим форматирование столбиков и защитим лист @007.

Геометрия радиусной кривой

Все расчеты по разным вариантам исходных данных:

Хорда L; Прогиб Н; Радиус R; Угол G.

Эти расчеты часто требуются для нахождения элементов детали имеющих форму сегмента окружности.

Рис. Геометрия радиусной кривой.

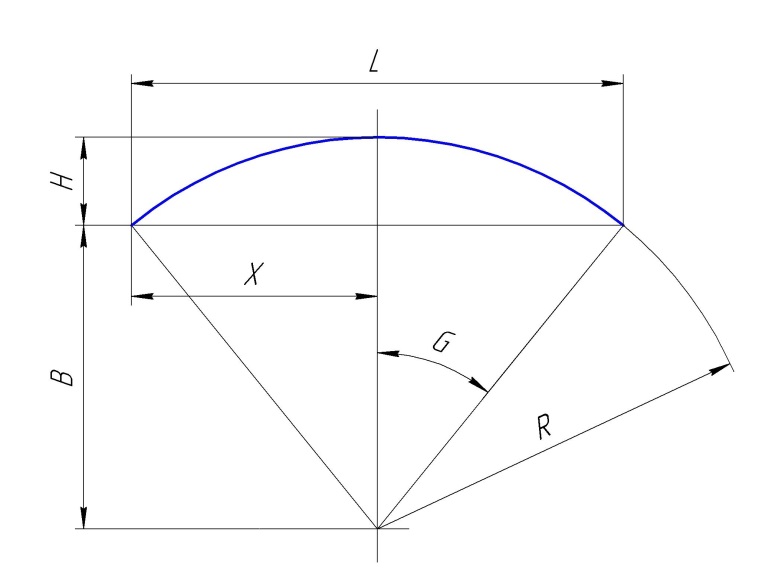
Расчет производим из следующих соотношений:

В = sqrt( R*R – X*X); L = X + X; H = R – B; G = аrcsin ( X / R );

Длина дуги = Pii * R * G / 90;

Площадь сектора Ss = Pii * R * R * G / 180;

Площадь треугольника под хордой St = L * B /2;

Площадь сегмента ( горбушки ) Sg = Ss – St;

Некоторые комбинации данных не позволяют прямого расчета,

тогда применяем метод компьютерного подбора.

Контрольный расчет:

Радиус R = 1000;

Диаметр D = R+R; D = 2000; Хорда L = 765,3668647;

Стрела прогиба максимальная H = 76,12046749;

Угол: Центр – Хорда: 2 * G = Au = 45 градусов..

Площадь сектора круга с углом = Au:

Sk=Pii*D*D* Au /(4*360); Sk = 392699,0816987241;

Площадь треугольника в секторе:

St=(L/2)* B; St = 353553,3905932738;

Площадь горбушки отсеченной хордой:

S = Sk-St; S = 39145,69110545033;

Длина дуги над хордой:

L=Pii*D*Au /360; L = 785,3981634;

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 15. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия радиусной кривой.». Далее форматируем столбики как описано @002. @003. @004. @004А.

Далее как в предыдущем.

Примечание: При исходных данных «Хорда – Прогиб» прямым расчетом не решается – применяем метод подбора с шаговым уточнением. В Excel програмные циклы запрещены – поэтому автоматический подбор запрограммировать не получится. Такие программы делаем в Python..

Координаты радиусной кривой

Построение части окружности методом подъема применяется тогда, когда радиус слишком велик

для традиционного построения, либо когда точка центра радиуса недоступна.

Если внутри контура кривой расположены объекты мешающие построению хорды, тогда строят линию, паралленьную хорде, с точкой касания в вершине кривой и от этой линии откладывают величины «Н2».

Рис. Координаты радиусной кривой.

,,,,

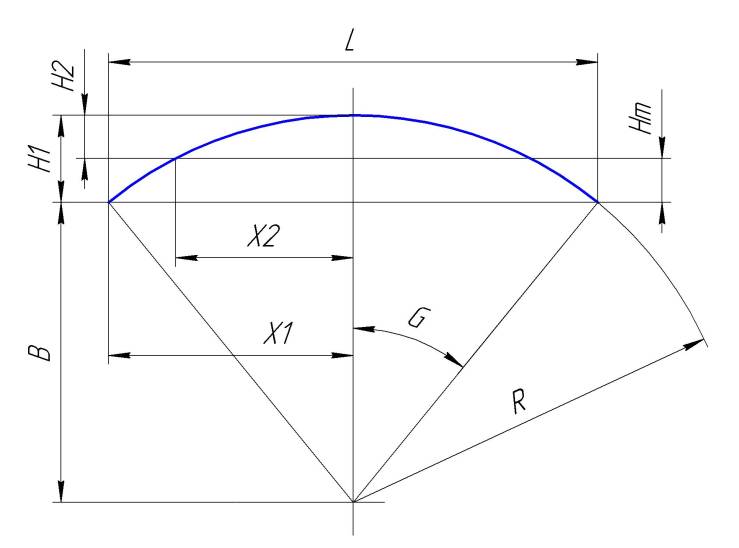
Построение части окружности методом подъема.

Построение:

Задаем максимальный размер хорды L.

Из середины максимальной хорды L строим перпендикуляр Н1.

Х1 = L / 2; В = sqrt( R*R – X1*X1); H1 = R – B;

Определили максимальную стрелу прогиба кривой H1.

Далее задаем произвольное расстояние от центральной оси Х2.

Находим стрелу прогиба Н2 = R – ( sqrt( R*R – X2*X2));

Находим высоту подъема в точке Х2: Hm = H1 – H2;

Задавая ряд текущих значений Х2 и рассчитывая соответствующие высоты подъема Hm

– получаем достаточное количество точек,

для построения радиусной кривой по точкам на этой кривой.

Контрольный расчет:

Исходные данные:

Радиус R = 10000;

Хорда максимальная заданная L = 8000;

Подъем максимальный в центре хорды = 834,8486100883201.

Задаем ряд точек:

От центра хорды до точки по оси Х-Х = 3000,0.

Величина подъема ( перпендикуляра ) = 374,2406242577763.

…

От центра хорды до точки по оси Х-Х = 2000,0.

Величина подъема ( перпендикуляра ) = 632,8075812210318.

…

От центра хорды до точки по оси Х-Х = 1000,0.

Величина подъема ( перпендикуляра ) = 784,7229811545203.

…

От центра хорды до точки по оси Х-Х = 500,0.

Величина подъема ( перпендикуляра ) = 822,3407878074104.

…

От центра хорды до точки по оси Х-Х = 0,001.

Величина подъема ( перпендикуляра ) = 834,848610088271.

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_15. ( Скачать из приложения ).

Сохраним его как Е 16. Далее на листе необходимо выполнить заголовок расчета:

Остальное аналогично предыдущему, формулы приведены выше, записи в Excel смотрите в открытом

Листе – скачать в приложении.

Расчет геометрии треугольника

Напротив сторон треугольника лежат одноименные углы.

Рис. Геометрия треугольника.

,,,

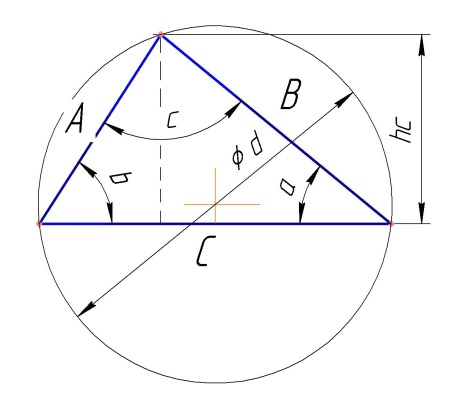
Известны три стороны треугольника

Напротив сторон треугольника лежат одноименные углы.

Сторона = a. Сторона = b. Сторона = c.

Решение:

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=аrccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=аrccos(x)… Угол В.

.cu=180-(au+bu)… Угол С.

Известны две стороны и угол между ними

Сторона = a; Сторона = b; Угол = cu..

Решение:

.с= sqrt ((a*a)+(b*b))-(2*a*b*(cos(cu)))… Сторона «с».

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=arccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=arccos(x)… Угол В.

Известны два угла и сторона между ними

Сторона = a; Угол = bu; Угол = cu;

Решение: .au=180-(bu+cu)… Угол А. .b=(a*(sin(bu)))/(sin(au))… Сторона В.

.c=(b*(sin(cu)))/(sin(bu))… Сторона С.

Добавочный расчет в алгоритм Треугольника

Решение:

R=a/(2*(sin(au))… R – Радиус описанной окружности.

.hc=b*(sin(au))… Высота из угла С.

.hb=a*( sin(cu))… Высота из угла B.

.ha=c*(sin(bu))… Высота из угла A.

S=a*ha/2.. Площадь треугольника.

Pe=a+b+c.. Периметр.

.rv=(S+S)/Pe… Радиус вписанной окружности.

…..

Контрольный расчет:

Напротив сторон треугольника лежат одноименные углы.

Сторона А = 15,77350269;

Сторона В = 14,14213562;

Сторона С = 11,54700538;

Угол А = 75; Угол В = 60; Угол С = 45..

Высота А= 10; Высота В = 11,1535507;

Высота С = 13,66025403;

Описанный радиус = 8,164965804;

Вписанный радиус = 3,804268442;

Площадь = 78,86751346;

Запись программы в Excel.

Смотри открытый и закрытый листы Е 17.. ( Скачать из приложения ).

Параметры сечений

Параметры сечения круга

Сечение – Круг

Диаметр круга d.

Контрольный расчет:

Круглое сечение: Диаметр = 80;

S=5026,548246; Jxx =2010619,298; Wxх=50265,48246.. .i=20,0…

Решение:

.s=d*d*Pii/4… Площадь круга.

.wr=Pii*d*d*d/16… Момент сопротивления радиальный.

.wx=wr/2… Момент сопротивления изгибу.

.jr=wr*d/2… Момент инерции радиальный.

.jx=jr/2 … Момент инерции по оси Х-Х.

.rm=sqrt(jx/s)… Радиус инерции оси Х-Х.

Расчет параметров трубного сечения.

Запись программы в Excel.

Смотри открытый и закрытый листы Е 18.. ( Скачать из приложения ).

Сечение – трубное

Наружный диаметр d.

Внутренний диаметр dv.

Рис. Сечение трубное круглое.

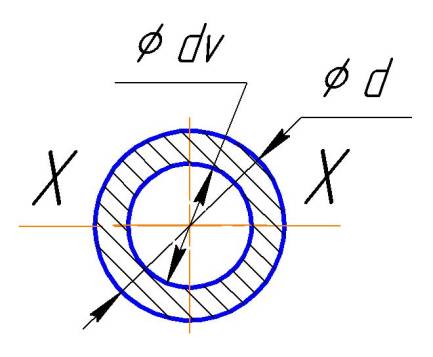
.x=(d-dv)/2… Толщина стенки трубы.

.sn=d*d*Pii/4… Площадь отверстия.

.sv=dv*dv*Pii/4… Площадь по внешнему контуру.

.s=sn-sv… Площадь трубного сечения.

.jrn=Pii*(d**4)/32…

.jrv=Pii*(dv**4)/32…

.jr=jrn-jrv… Момент инерции радиальный.

.jx=jr/2… Момент инерции по оси Х-Х.

.wr=jr*2/d… Момент сопротивления радиальный.

.wx=wr/2… Момент сопротивления изгибу.

.rm=0,25*(sqrt(d*d+dv*dv))… Радиус инерции оси Х-Х.

Контрольный расчет:

Круглое трубное сечение: Диаметр = 80; Отв. Ф = 60..

Площадь сечения S=2199,11485751;

Jxx =1374446,785946; Wxх=34361,1696486.. .i=25,0..

Запись программы в Excel.

Смотри открытый и закрытый листы Е 19.. ( Скачать из приложения ).

Параметры сечения прямоугольника

Сечение – Прямоугольник

Высота сечения h.

Ширина сечения b.

Контрольный расчет:

Прямоугольное сечение: Высота = 80; Ширина = 60..

S=4800; Jxx =2560000; Wxх= 64000..

Jyy =1440000; Wyy= 48000.. .i=17,320510…

Диагональ = 100..

Рис. Сечение прямоугольника.

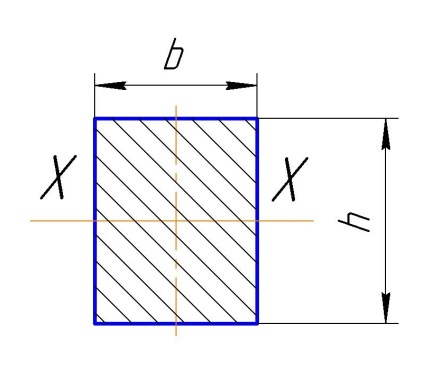
.s=h*b… Площадь прямоугольника.

.dg =sqr ((b*b)+(h*h))… Диагональ прямоугольника.

.jx=b*h*h*h/12 … Момент инерции по оси Х-Х.

.wx=b*h*h/6… Момент сопротивления изгибу по оси Х-Х.

.jy=h*b*b*b/12… Момент инерции по оси Y-Y.

Выбираем меньшее значение момента инерции «j min».

.rm=sqrt(j min/s)… Радиус инерции минимальный.

Расчет параметров сечения прямоугольной трубы.

Запись программы в Excel.

Смотри открытый и закрытый листы Е 20.. ( Скачать из приложения ).

Сечение – Прямоугольная труба

Высота сечения h.

Ширина сечения b.

Высота отверстия hm.

Ширина отверстия bm.

Рис. Сечение прямоугольной трубы.

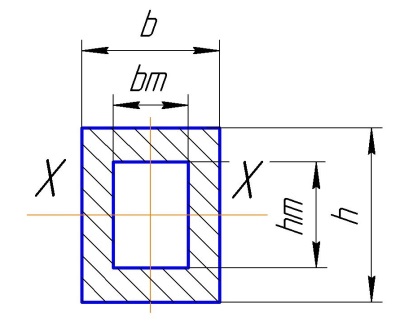
Расчет:

.s=(h*b)-(hm*bm)… Площадь сечения прямоугольной трубы.

.jx=(b*h*h*h/12)-(bm*hm*hm*hm/12)… Момент инерции по оси Х-Х.

.wx=2*jx/h… Момент сопротивления изгибу по Х-Х.

.jy=(h*b*b*b/12)-(hm*bm*bm*bm/12)… Момент инерции по оси Y-Y.

.wy=2*jy/b… Момент сопротивления изгибу по Y-Y.

Выбираем меньшее значение момента инерции «j min».

.rm=sqrt(j min/s)… Радиус инерции минимальный.

.rmm= sqrt(((b*h*h*h) – (bm*hm*hm*hm))/(12*.s))..

Контрольный расчет:

Прямоугольная труба.

Высота = 80;

Высота отв.= 60;

Ширина = 60..

Ширина отв.= 40..

S=2400; Jxx =1840000; Wxх= 46000.. Jyy =1120000; Wyy= 37333,(3)..

.rm=21,60246899… .rmm=21,6025…. Диагональ = 100..

Запись программы в Excel.

Смотри открытый и закрытый листы Е 21.. ( Скачать из приложения ).

Сечение – Треугольник

Высота треугольника h.

Основание треугольника b.

Центр тяжести ЦТ. От основания до ЦТ размер Z.

Центр тяжести находится на одной трети высоты от любой стороны.

Ось Х-Х проходит через Ц.Т. и параллельна основанию.

Ось Y-Y проходит через Ц.Т. и перпендикулярна основанию.

Рис. Сечение треугольника.

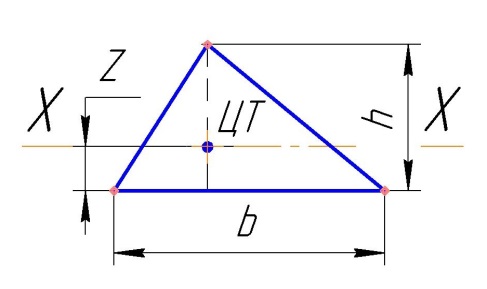
Расчет:

Sk=(h*b)/2… Площадь сечения.

Jxk=b*h*h*h/36… Момент инерции по оси Х-Х.

Для волокна вершины треугольника:

Mik=Jxk/(h*2/3)… Момент сопротивления изгибу по оси Х-Х.

Для волокна основания треугольника:

Mio=Jxk/(h*1/3)… Момент сопротивления изгибу по оси Х-Х.

Rk=sqrt(Jxk/Sk)… Радиус инерции сечения.

Z=h/3… Высота Ц.Т. от основания.

Контрольный расчет:

Треугольное сечение: Высота=80; Основание=60;

S=2400; Z =26,6(6); от подошвы до центра тяжести..

Jxx =853333,3(3); Wxn=32000,0; для нижних волокон..

Wxv=16000,0; … для верхних волокон..

.i=18,85618083..

……

Jy=h*b*b*b/48…

Запись программы в Excel.

Смотри открытый и закрытый листы Е 22.. ( Скачать из приложения ).

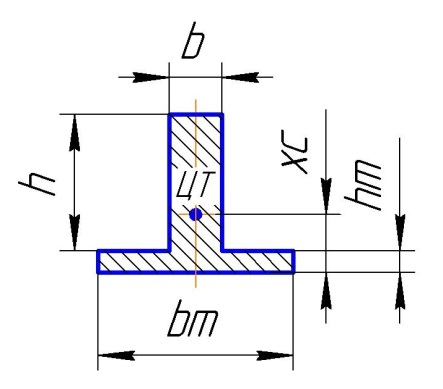
Сечение – Тавр

Высота пера h.

Толщина пера b.

Высота подошвы hm.

Ширина подошвы bm.

Центр тяжести ЦТ. От подошвы до ЦТ расстояние xc.

Ось Х-Х проходит через Ц.Т. и параллельна основанию.

Ось Y-Y проходит через Ц.Т. и перпендикулярна основанию.

Рис. Тавр.

Контрольный расчет:

Тавровое сечение:

Высота ребра = 80.. Толщина ребра =20..

Ширина подошвы = 60.. Толщина подошвы = 40..

Площадь S=4000.;

XC=44,0..; от подошвы до центра тяжести..

Jxx =4629333,(3)..

Х-Х – параллельна подошве..

Wxx=60912,28070175;.. минимальное..

Jyy=773333,(3)..;

Wyy=25777,(7);..

Радиус инерции .i= 13,90444.. минимальное..

…….

Расчет:

.s=(h*b)+(hm*bm)… Площадь сечения тавра.

.j1=b*h*h*h/12… Момент инерции пера относительно Ц.Т. пера.

.j2=bm*hm*hm*hm/12… Момент инерции подошвы относительно Ц.Т. подошвы.

.f1=h*b… Площадь пера.

.f2=hm*bm… Площадь подошвы.

.x1=(h/2)+hm…

.x2=hm/2… Gsf = 461030/2725231222…

Центр тяжести тавра от низа подошвы «xc».

.xc=((f1*x1)+(f2*x2))/(f1+f2)…

.r1=(((h/2)+hm)-xc)… Радиус ц.т. пера от ц.т. тавра.

.r2=xc-(hm/2)… Радиус ц.т. подошвы от ц.т. тавра.

.jx1=j1+(r1*r1*f1)… Момент инерции смещенного пера.

.jx2=j2+(r2*r2*f2)… Момент инерции смещенной подошвы.

.jx=jx1+jx2… Момент инерции тавра по Х.

.wx=jx/((h+hm)-xc)… Момент сопротивления изгибу тавра по Х.

.jy1=h*b*b*b/12…

.jy2=hm*bm*bm*bm/12…

.jy=jy1+jy2… Момент инерции тавра по Y.

.wy=jy/(bm/2)… Момент сопротивления изгибу тавра по YY.

Выбираем меньшее значение момента инерции «j min».

.rm=sqrt(j min/s)… Радиус инерции минимальный.

Запись программы в Excel.

Смотри открытый и закрытый листы Е 23.. ( Скачать из приложения ).

В колонке «Е»расчет промежуточных величин.

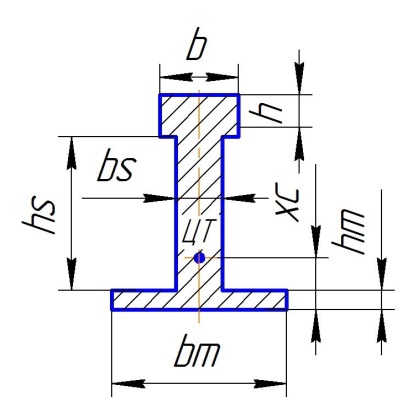
Параметры сечения рельса

Высота головки = h.

Ширина головки = b.

Высота стенки = hs.

Толщина стенки = bs.

Ширина подошвы = bm.

Толщина подошвы = hm.

Ось Х-Х проходит через Ц.Т. и параллельна основанию ( подошве ).

Ось Y-Y проходит через Ц.Т. и перпендикулярна основанию.

Рис. Рельс.

Контрольный расчет:

Сечение типа Рельс:

Высота головки = 40..

Ширина головки =60..

Высота ребра = 80..

Толщина ребра =20..

Ширина подошвы = 100..

Толщина подошвы = 10..

S=5000.;

XC =69,80..; от подошвы до центра тяжести..

Jxx =9886466,(6)..

Х-Х – параллельна подошве..

Wxx=141639,923591;.. минимальное..

Jyy=1606666,(6)..

Wyy=32133,(3);..

.i= 17,925773.. минимальное..

……

Расчет:

.s=(h*b)+(hm*bm)+(hs*bs)… Площадь сечения рельса.

.j1=b*h*h*h/12… Момент инерции головки относительно собственного Ц.Т.

.j2=bs*hs*hs*hs/12 … Момент инерции стенки относительно собственного Ц.Т.

.j3=bm*hm*hm*hm/12… Момент инерции подошвы относительно собственного Ц.Т.

.f1=h*b … Площадь головки.

.f2=hs*bs … Площадь стенки.

.f3=hm*bm… Площадь подошвы.

.x1=(h/2)+hs+hm …

.x2=(hs/2)+hm…

.x3=hm/2…

Центр тяжести рельса от подошвы «xc».

.xc=((f1*x1)+(f2*x2)+(f3*x3))/(f1+f2+f3)…

.r1=((h+hs+hm)-h/2)-xc… Радиус ц.т. головки от ц.т. рельса.

.r2=((hs/2)+hm)-xc… Радиус ц.т. стенки от ц.т. рельса.

.r3=xc-(hm/2)… Радиус ц.т. подошвы от ц.т. рельса.

.jx1=j1+(r1*r1*f1)… Момент инерции смещенной головки.

.jx2=j2+(r2*r2*f2)… Момент инерции смещенной стенки.

.jx3=j3+(r3*r3*f3)… Момент инерции смещенной подошвы.

.jx=jx1+jx2+jx3… Момент инерции рельса по ХХ.

.wx1=jx/((h+hs+hm)-xc)… Момент сопротивления изгибу рельса по ХХ.

.wx=jx/xc… Момент сопротивления изгибу рельса по ХХ.