
Полная версия
Властелин механики. 7 великих законов в понятном изложении
Стандартное определение понятия в физике, всё же, существует. Им и будем пользоваться для дальнейшего объяснения. Более глубокие мысли хоть и интересны, но уже выходят за границы раздела механики и к ним мы вернемся в других работах.
Энергия – скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. С древнегреческого языка оно переводится как действие.
Если опустить ряд сложностей, которые не особенно и нужны для понимания применительно к механическим процессам, то всё равно разобраться будет не так-то просто. Перечитав это определение несколько раз, вы вероятно так и не поймете, о чем там написано. Давайте разобьем стандартное определение на фрагменты, а после этого запишем его в более понятной и простой форме.
Скалярная – означает не имеющая направления. Про это поговорили в самом начале книги. Но давайте закрепим на будущее. Это величины, как масса тела или атмосферное давление. Они просто есть и не связаны с движением. Для сравнения – скорость величина векторная, имеет направление. Чувствуете разницу между скоростью и массой? Вот именно такая разница и между векторными и скалярными величинами.
Следующая часть определения говорит, что мы имеем дело с некоторой мерой взаимодействия тел. Причем, применительно к любым видам взаимодействия. Но нас сейчас интересует механика. И тут уместно назвать это именно что «мерой взаимодействия».
Представьте, что вы поддали мячик ногой. Вы передали мячику что-то и это что-то потом начало оказывать воздействие разных типов. Что-то и есть энергия. Или «движение» если обратиться к переводу слова. Его иначе не назовешь. Вот и придумали фразу про меру воздействия, добавив её в определение энергии.
Ещё можно представить камень, который падает кому-то на голову с крыши. Сразу вспоминается великолепный эпизод из фильма «Один дома 2», где Кевин кидается кирпичами в Марва. Вот летящий камень обладает чем-то, что он потом передаст голове нашего отрицательного героя. Это что-то и есть энергия. Или вновь подойдет слово движение. Почему мы так размыто разъясняемся? Наверное потому, что даже механическую энергию, которая наиболее проста для восприятия, пока всё ещё не могут описать в полной мере и дать однозначное определение понятия.
Но для наших целей достаточно указанного выше определения. В целом-то, воспринимать слово механическая энергия, как слово «движение» вполне допустимо. Будут проблемы с представлением потенциальной энергии сжатой пружины, но там мы скажем, что сжатая пружина запасла некоторое количество движения и опять логику передадим.
Закон сохранения энергии в кино и философии
Закон сохранения энергии описывается разными словами и носит разные имена. Интересно отметить, что логика сохранения энергии пронизывает многие философские книги и даже современные фильмы.
Например, в фильме «Звёздные войны» присутствует такая характеристика, как сила. Силой там именуется некоторая субстанция, которую можно использовать как во благо, так и во вред. Но сама по себе сила нейтральна.
Очень легко провести параллели между силой в этом фильме и энергией в нашей жизни. Ведь по философским представлениям, да и по физическим законам, появившимся чуть позже, энергия во вселенной не появляется и не пропадает, а просто превращается из одной формы в другую форму. Аналогично этому представлению, герои Звездных войн как раз-таки и использовали силу, которая не появлялась и не пропадала, а только передавалась от одного объекта другому.
Подобный процесс передачи энергии или силы демонстрировался в некогда популярном фильме «Горец». Когда бессмертному отрубали голову его энергия передавалась победителю в виде разряда молнии.

Рис.12. Молния передает нечто, что мы называем энергия
В философии понятие «энергия» встречается очень часто и только ленивый не попробовал как-то объяснить происходящее. Античные философы описывали энергию как нечто, способное совершать работу и имеющее внутри себя силы. Примерно так описывал это Аристотель.
Фома Аквинский характеризовал энергию как акт чего-либо. Обеспечение процесса живительным действием.
Ну а «божественные теории» относительно термина энергия встречаются в философии регулярно.
Так, сила, которой обладают боги, тоже подходит под определение энергии. Люди могли обратиться к богам и попросить у них эту силу, а сила передавалась и превращалась бы в другие формы деятельности. Например, в случае языческих представлений, она переходила в рост урожая или приводила к появлению дождей.
Сколько убыло столько и прибыло
Физика выделяет разные виды энергии. Они могут неограниченно превращаться из одного вида в другой. Если в одном процессе энергия израсходована, то в другом смежном процессе её гарантированно стало больше. Но об этом чуть позже. Сейчас же запомним, что энергии характерны превращения из одного вида в другой.
Ударьте рукой по столу. А теперь проанализируйте, куда именно была израсходована энергия удара и как она превращалась из одной формы в другую.
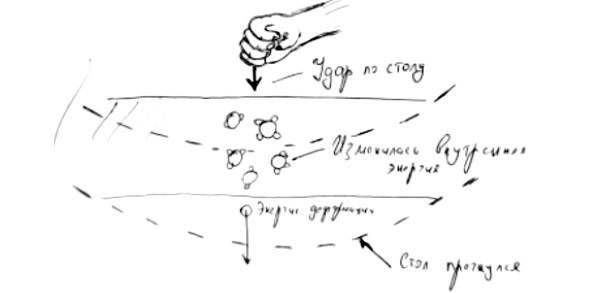
Рис.13. Превращение энергии при ударе рукой по столу
Понятие превращения энергии одно из самых важных в физике. Причем, вне зависимости от раздела. Понятно, что нам сейчас интересна механика, но все принципы работают и в других сферах.
Энергии свойственно переходить из одной формы в другую. Относительно механики выделяют два основных типа энергии. Есть ещё третий, который относится к другому разделу физики из-за своей природы, но на механические процессы также оказывает влияние.
Виды энергии применительно к механике
В механике обычно выделяют два основных вида энергии. Это кинетическая и потенциальная энергии. Есть ещё внутренняя энергия. Это тот самый третий вид, про который мы упомянули. Она тоже частенько трётся где-то рядом, но к механической энергии как такового отношения не имеет.
Правда в задачах, да и в стандартных жизненных ситуациях, связанных с механическим взаимодействиями, внутренняя энергия всегда фигурирует.
Внутренней энергией называется энергия, которой обладает структура тела, его атомы и молекулы. При взаимодействиях этих частиц происходит повышение температуры изучаемого тела. Так, ударив молотком по гвоздю, мы повысили внутреннюю энергию гвоздя посредством механического воздействия. Это воздействие вызвало чехарду в структуре тела и взаимных движениях части внутри него, что привело к нагреванию.
Теперь подробнее про кинетическую и потенциальную энергии.
Кинетическая энергия – та энергия, которой обладают движущиеся тела. Вот, собственно говоря, и всё. Летит в нас мячик и мячик имеет кинетическую энергию, которая будет частично передана нам при ударе.
Рис.14. Летящий мячик обладает кинетической энергией
Всегда, когда речь заходит о кинетической энергии, мы имеем дело с движением. Не случайно кинетическая энергия рассчитывается по формуле:
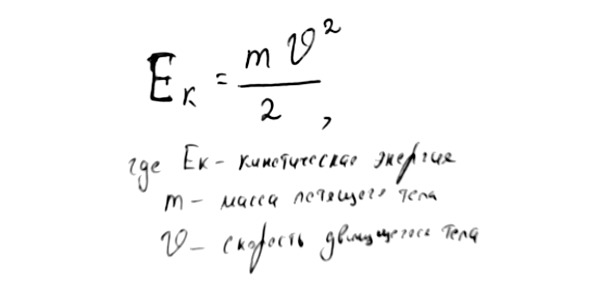
В расчёте участвует скорость, которая обозначена тут буквой V. Само собой, масса (m) тоже будет присутствовать в этом расчёте. Ведь чем массивнее тело, тем сильнее оно может ударить или, говоря научным языком, тем большее количество энергии оно может запасти при движении с некоторой скоростью.
Потенциальная Энергия – это энергия, которая есть у покоящегося тела и которая может высвободиться при изменении некоторых условий.
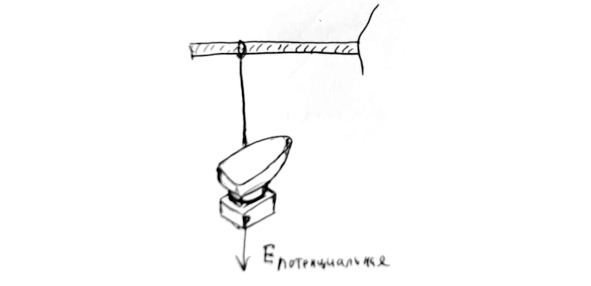
Рис.15. Наковальня висит на веревке и обладает потенциальной энергией, а если её отрезать, то энергия высвободится
Представим себе, что на ниточке подвешен камень. Пока камень подвешен, он обладает потенциальной энергией. Если камень начнет вдруг падать, то эта потенциальная энергия высвободится. Высвобождение будет сопровождаться превращением потенциальной энергии камня в его кинетическую энергию. Ведь у него появится и скорость, и масса (которая никуда и не пропадала).
Заметьте, что, когда речь заходит о потенциальной энергии, чаще всего мы говорим о падении чего-нибудь куда-нибудь. Даже рассчитывается потенциальная энергия по простой формуле:

Тут тоже есть масса m, ускорение свободного падения g и высота, с которой будет падать тело h.
Если же речь идёт про сжатую пружину, то схема расчёта слегка иная.

Здесь есть деформация пружины x и жесткость пружины k.
Хотя формула и похожа на расчет кинетической энергии, но тут мы имеем абсолютно другой физический смысл. Экспериментальные исследования позволили выяснить, что энергии будет вот столько, но факт того, что величины считаются похожим образом ни о чем не говорит. В одном случае происходит движение со скоростью, а в другом случае есть внутренние взаимодействия в теле, которые вызывают явление упругости.
Кстати говоря, сжатая пружина как нельзя лучше подходит для демонстрации явления потенциальной энергии. Глядя на неё не сложно понять всю суть рассматриваемой проблемы. Мы сжали пружину и пока она находится в таком состоянии, внутренние силы стараются её распрямить. Стоит её отпустить, и пружина отлетит в лоб. Вспомним шутку из Симпсонов, когда Гомер открыл банку от чипсов и оттуда в глаз ему вылетела пружина, с которой он потом бегал по городу. Это и была потенциальная энергия, превратившаяся в кинетическую.

Рис. 16. Сжатая пружина может отлететь в глаз
Всегда, когда речь заходит о кинетической энергии, мы имеем дело с движением. Не случайно кинетическая энергия рассчитывается по формуле:
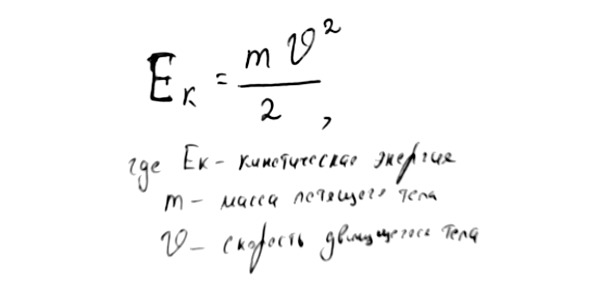
В расчёте участвует скорость, которая обозначена тут буквой V. Само собой, масса (m) тоже будет присутствовать в этом расчёте. Ведь чем массивнее тело, тем сильнее оно может ударить или, говоря научным языком, тем большее количество энергии оно может запасти при движении с некоторой скоростью.
Ну и анализируя теперь пример с рукой и столом, который был в самом начале обсуждения, мы можем провести более глубокий анализ процесса.
Пока рука приближалась к столу, присутствовала кинетическая энергия, которая в итоге была передана столу и вызвала его незначительную деформацию. Несколько миллисекунд, пока стол не вернулся к своей исходной форме, он обладал потенциальной энергией. Сразу произошло несколько интересных процессов — один вид энергии превратился в другой вид энергии, а ещё сработал закон сохранения энергии.
Пример, вероятно, не самый полный и может показаться, что мы попросту забыли о некоторых моментах. Скажем, мы не учли, что деформируется и сама рука. Но в физике принято исключать малозначимые факторы и процессы или пренебрегать ими.
Строится принципиальная схема, а некоторые объекты вполне можно принимать за материальные точки, недеформируемые тела и делать прочие упрощения. Таких допущений огромное количество. Они есть в каждом учебнике при разборе ситуаций. Ведь не внеси мы такое упрощение и самая простая задачка про брусок и наклонную плоскость будет решаться этак на 100 страницах!
В случае с рукой мы исключили множество моментов – стол нагрелся от удара, рука тоже деформировалось, насколько бы это не было сложным для беглого восприятия, но у движущегося тела присутствовала и потенциальная энергия и многие другие. Мы всё это упрощаем для того, чтобы сосредоточиться на основном явлении.
Но! Это не означает, что все остальные факторы пропали вовсе! Они есть. Мы понимаем, что их влияние минимальное и отбрасываем их. Если же считать «по уму», то следует проводить сложнейшие интегральные вычисления и схемку рисовать покруче. Подобные вычисления потребуются, разве что, при проектировке самолета.
Формулируем закон сохранения механической энергии
Из этих нехитрых примеров следует, что при механических воздействия энергия может неограниченное количество раз превращаться из одного вида в другой. Потенциальная энергия переходит в кинетическую, а кинетическая переходит в потенциальную.
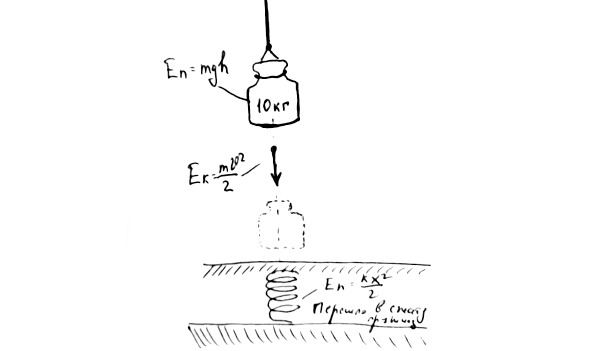
Рис.17. Превращение энергии при падении гири на пружинный пол
Когда речь идёт о механической энергии всегда рассматривается сумма механической и потенциальной энергий. Это будет так называемая полная энергия системы.
Рассуждения о превращении энергии подталкивают к мысли, что на самом-то деле энергия не появляется и не пропадает. Она просто превращается из одной формы энергии в другую с потерями на другие процессы. И мы пришли к закону сохранения механической энергии.
Закон сохранения энергии гласит, что энергия ниоткуда не возникает и никуда не пропадает. Энергия лишь переходит из одного вида в другой или от одного тела к другому.
Как вы заметили, слово «механической» тут отсутствует. Закон справедлив не только для механики. Как и понятие «энергия» закон сохранения значим для всей физики сразу вне зависимости от раздела. Он работает во всей вселенной.
Но применительно к механике закон сохранения энергии учитывает преимущественно кинетическую энергию тела, потенциальную энергию тела и иногда ещё внутреннюю энергию тела (если происходит передача энергии движения в нагрев и т.п.), о которых мы поговорили чуть выше.
Теперь посмотрим, как сформулирован закон сохранения механической энергии в учебниках:
В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔЕ = 0
или Е потенциальная 1 + Е кинетическая 1 = Е потенциальная 2 + Е кинетическая 2
или как вы это привыкли видеть:

Почему замкнутой? Потому что если система не замкнутая, то она будет обмениваться энергией с другими участниками процесса, и энергия в итоге рассеивается. Тот самый пример со столом подходит как нельзя лучше.

Рис.18. Человек, закрытый в ящике – это замкнутая система
Скажем, запустили мы всем известные шарики для демонстрации закона сохранения импульса. Они качаются и передают друг другу энергию в одной замкнутой системе.
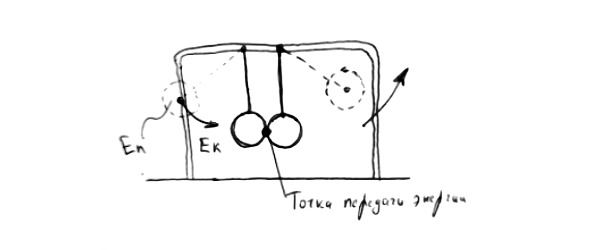
Рис.19. Постоянная передача энергии с её превращением в замкнутой системе
Замкнутая система тут – это рама с нитями и сами шарики. Будь система не замкнутая, шарики должны были бы бить, скажем, ещё и по внешней стенке и отдавать ей часть своей энергии. Практически любую систему условно можно воспринимать, как замкнутую. Этот принцип активно используется при решении задач. Ключевое слово тут условно. Потому что копни поглубже и увидишь, что ни одна замкнутая система не будет замкнутой.
Почему консервативная и что это значит? Потому что если на систему воздействуют внешние силы, то они внесут свой вклад в процесс и уравнение, где общее изменение энергии равно нулю уже будет несправедливым. Консервативная система есть та, где существуют только консервативные силы.
Сила называется консервативной если ее работа не зависит от траектории, а определяется только начальным и конечным положениями тела.
Можно сказать и по-другому. Все действующие на систему внешние и внутренние непотенциальные силы не должны совершать работы, а все потенциальные силы должны быть стационарны. Это и будет консервативная система.
Проще было бы сказать что-то из серии – система варится в своем соку и ни с чем не взаимодействует. Логика бы сохранилась, а формулировка упростилась.

Рис.20. Жук внутри консервативной системы
Следовательно, если рассматривать систему, где происходит механическое движение и подул ветер, который заставил тело получить внешнюю энергию, она уже не консервативная. Модель движения автомобиля по дороге далеко не консервативная.
Правда тут возникает один интересный вопрос… Часто обозначенные выше обстоятельства воспринимаются как те, которые мешают работать закону сохранения энергии. Это не совсем так.
Закон сохранения энергии работает всегда. Вне зависимости от того, консервативная ли у нас система и замкнутая ли она. Только вот записать тогда его в форме, привычной нам из школьного курса, уже не получится. Реальная картина будет намного сложнее. Приведенная формулировка закона сохранения механической энергии используется для упрощения ситуации.
Так, простой пример с падением срезанной с веревки гири на пол можно значительно усложнить. Гиря висела на веревке, обладала потенциальной энергией. Веревку отрезали. Потенциальная энергия должна была полностью передаться падающей гири и превратиться в кинетическую, но мы не учли, что была ещё веревка, которая тоже получила часть этой энергии. Пока гиря падала, она воздействовала на воздух и испытывала трение о воздух. Нагрелись воздух и гиря. При падении она частично сломала пол, на который, растратив на разрушение часть энергии ну и частично перешла во внутреннюю энергию.
И пусть всё это значения с приставкой микро-, но реальная картина должна учитывать каждую мелочь. Прыгающий мяч в реальности рано или поздно остановится. Всё из-за постоянных взаимодействий.
Отсюда было логично предложено упрощать подобные взаимодействия и рассматривать гипотетические консервативные и замкнутые системы.
Ну а закон сохранения при таком рассмотрении сводится к простому примеру: висела люстра и обладала потенциальной энергией. Кинетическая энергия этой люстры была равна нулю. Потом веревочку обрезали, и кинетическая энергия появилась из-за превращения потенциальной энергии люстры в кинетическую. Если записать это в виде того самого выражения, что было приведено выше, где Еп1+Ек1=Еп2+Ек2 получим что-то вида 200 Дж +0 Дж = 0 Дж +200 Дж. Кинетическая и потенциальная энергия поменялись местами.
Для решения большей части практических задач достаточно такого понимания процесса и таких знаний.
В чем измеряется энергия
Мы обсудили закон сохранения энергии и даже привели примеры, но так и не упомянули, какая у энергии единица измерения.
Поскольку энергия у нас является мерой совершения телом работы, то и измеряется она в тех же величинах, что и работа. Единицей измерения энергии в системе СИ принят Джоуль.
Но есть и другие системы измерения. Например, в системе СГС энергия измеряется в эргах. Это довольно редкая единица и скорее всего, она вам никогда и не встретится. Но знать про это полезно. Собственно, 1 эрг = 1 дин х 1 см или та же самая сила, умноженная на расстояние, или работа по-нашенски.
Вы наверняка не в курсе, что система СГС – это система единиц измерения, в которой основными единицами являются единица длины сантиметр, единица массы грамм и единица времени секунда.
Ещё в технических расчетах встречается такая единица измерения энергии как килограммометр (кгм) или килограмм силы (кгс) на метр (м): (кгсм). При этом считают, что 1кгсм=1 кгс⋅1 м=9,81 Дж.
Есть и другие варианты единицы измерения энергии, но к механике они отношения не имеют. Например, существуют калории, кВт*ч или электрон-вольты. Единица измерения никак не влияет на факт существования физического понятия или процесса и нужна только для некоторой систематизации.
Почему невозможно создать вечный двигатель
Исходя из закона сохранения механической энергии складывается ложное впечатление, что возможно создать вечный двигатель. Ведь для работы такого агрегата будет достаточным просто играться с превращениями энергии. Это вполне не сложно и может быть реализовано с помощью современных технологий.
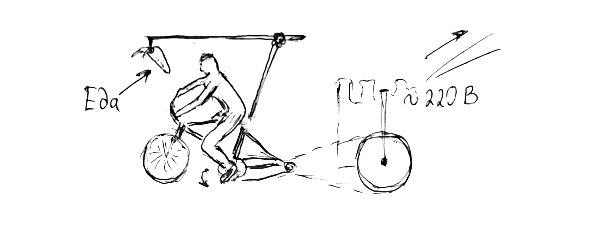
Рис.21. Модель вечного двигателя
Скажем, скатилось какое-то тело с наклонной плоскости и, обладая инерцией, оно может заехать на другую наклонную плоскость и на ту же самую высоту. Ведь мы выяснили, что энергия передается в полном объеме исходя из закона сохранения энергии.
Делая такие правильные с точки зрения здравого смысла предположения, мы не учитываем все сложности взаимодействий, с которыми приходится столкнуться в реальности. Закон сохранения энергии тут нам вряд ли поможет. Он скорее опишет лишний раз, почему вечный двигатель создать невозможно, а перпетум мобиле останется и дальше уделом фантастов.
Несмотря на то, что энергия неограниченно превращается и передается, нам гарантированы сопутствующие потери. Потери на самые разные вещи. Энергия рассеивается, также как рассеиваются силы у человека в течение рабочего дня. Вот поехали мы на работу и пока ехали уже устали. Виновато метро или любая другая форма транспорта.
Такая же ситуация и с сохранением энергии. Представим даже тот самый пример с наклонной плоскостью. Объект съедет по наклонной плоскости, но на такую же высоту у новой наклонной плоскости уже не заедет. Ведь будут потери на трение. И это как минимум. На самом деле потерь будет гораздо больше и их аналитика займет немалое количество времени.
Вы можете сказать – ну замените тело колесом, вот оно и будет скатываться без потерь. Ведь экстремалы в параболической рампе вполне себе неплохо справляются с обозначенными задачами и кажется, что скатываясь туда-обратно, они делают это только лишь по инерции. Это совсем не так. Опять беглый взгляд на проблему. Там тоже есть потери. Как минимум, на сопротивление воздуху. Кстати, если повторить опыт в вакууме, всё равно вечного двигателя не получится. Энергия будет рассеиваться на тепловую энергию, которая появится во втулках велосипеда или скейтборда, крутящегося в этой рампе.
Выходит, что закон сохранения энергии в правильном его изложении никоим образом не приближает нас разработке вечного двигателя. Он, наоборот, рассказывает, почему такой двигатель мы никогда не сделаем. В данном случае мы расписали самые простенькие примеры, но вне зависимости от конструкции и принципа работы агрегата главный физический принцип обмануть имеющимися методиками не получится.
Самое важное про закон сохранения энергии
Мы не случайно рассмотрели закон сохранения механической энергии самым первым. Для властелина механики он один из главных законов. Ведь без энергии не будет и работы. Чем тогда властвовать и кому нужна механика без движения. Да и обманщиков хватает. Скажем, вечные двигатели многократно пытались представить как реальные установки, используя в качестве движущей силы механизмы с хомяком в колесе или карликом, который едет на велосипеде внутри бочки. Всё это быстро становится понятным, если знать основы физической теории.

Рис.22. Белка в колесе – тоже вечный двигатель


