Полная версия
Сверхсветовая передача сигналов

Петр Путенихин
Сверхсветовая передача сигналов
Введение
Явление запутанности непосредственно следует из математического формализма квантовой механики. В соответствии с первым постулатом квантовой механики состояние квантовой частицы полностью описывается её волновой функцией. Однако в некоторых случаях квантовым частицам не удаётся приписать индивидуальные волновые функции, а только одну на всех. Такое состояние частиц названо запутанностью. Это состояние удалось получить на реальных частицах, например, в так называемых процессах параметрического распада, преобразования с понижением частоты (down conversion) на специальных кристаллах.
Физическое проявление запутанности в формализме квантовой механике получило собственное имя – нелокальность как антагонизм так называемому локальному реализму Эйнштейна, который не допускал пространственноподобной зависимости между запутанными частицами. Он предполагал, что экспериментально наблюдаемая связь между частицами на самом деле формируется в момент их запутывания и сохраняется до конца опыта. То есть, случайными состояния частиц формируются в момент их разделения. В дальнейшем они сохраняют полученные при запутывании состояния, и «хранятся» эти состояния в неких элементах физической реальности, описываемых «дополнительными параметрами», поскольку измерения над разнесенными системами не могут влиять друг на друга:
«Но одно предположение представляется мне бесспорным. Реальное положение вещей (состояние) системы S2 не зависит от того, что проделывают с пространственно отделённой от неё системой S1» [4, c.290].
«… так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой, во второй системе уже не может получиться никаких реальных изменений» [5, с.608].
К истокам возникновения таких взглядов на квантовую механику можно по праву отнести парадокс Эйнштейна-Подольского-Розена (ЭПР-парадокс), которые считали, что квантовая механика неполна, поскольку обнаруженная сверхсветовая корреляция запутанных частиц допускает одновременное определение некоммутирующих параметров системы, запрещаемое формализмом теории. Именно эти предположения и получили в дальнейшем название локального реализма Эйнштейна:
«Насчет того, что понимать под нелокальностью в КМ, то в научной среде, я считаю, сложилось некоторое согласованное мнение на этот счет. Обычно под нелокальностью КМ понимают то обстоятельство, что КМ противоречит принципу локального реализма (его еще часто называют принципом локальности Эйнштейна). Принцип локального реализма утверждает, что если две системы A и B пространственно разделены, тогда при полном описании физической реальности, действия, выполненные над системой A, не должны изменять свойства системы B» [3].
Нелокальность, мгновенная корреляция между запутанными квантовыми частицами является одним из самых загадочных явлений физики. Буквально её сущность можно выразить фразой "связь есть, но её нет". Проявляется эта связь при передаче так называемой квантовой информации между запутанными парами квантовых частиц. При измерении состояния одной из частиц пары вторая частица мгновенно и на пространственноподобном расстоянии также переходит в собственное состояние, будто и над ней произведена операция измерения. При этом состояние второй частицы строго коррелировано с состоянием первой. Получается, что первая частица как бы передает второй частице некоторую информацию со сверхсветовой скоростью.
Собственно носитель этой информации зарегистрировать в настоящее время не удалось, поэтому передача информации посредством нелокальной связи считается невозможной. На роль носителя этой неуловимой квантовой информации может претендовать гипотетическая частица – тахион, также не обнаруженный ни в одном эксперименте.
Вместе с тем возникает некоторая взаимосвязь явлений: если происходит какое-то взаимодействие со сверхсветовой скоростью, которое обнаружено в реальном физическом эксперименте – квантовая телепортация, то мы обязаны признать, что существует и некий реально существующий физический, материальный носитель этой информации. Следовательно, должна существовать и возможность сверхсветовой передачи уже не только мистической квантовой информации, но и реальной, классической информации.
Как известно, явление квантовой телепортации обнаружено исключительно математическими средствами в рамках квантовой информатики. Уравнения любых допустимых унитарных преобразований квантовых систем, то есть, преобразований, не приводящих к переходу квантовых частиц в собственные состояния, не содержат параметра времени и расстояний. Это ведет к естественному предположению о мгновенной передаче состояний объектов связанной, единой квантовой системы друг другу, причем на любом расстоянии.
На основе аналитических уравнений была разработана установка для передачи состояния от одной частицы запутанной пары к другой. Передаваемое состояние является произвольным и может быть неизвестно передающей стороне. Но проблема не в этом: даже зная состояние передаваемой частицы, мы не можем мгновенно узнать состояние частицы, переданное удаленной стороне. Это возможно лишь с использованием дополнительной, классической информации. Иначе говоря, считается строго доказанным, что сверхсветовая передача классической информации посредством квантовой телепортации невозможна. Главным аналитическим критерием в этом вопросе стали так называемые неравенства Белла, утверждающие, что никакие вероятностные корреляции невозможны без сверхсветовой передачи информации.
Собственно, понятие "неравенства Белла" породила статья Д.Белла "Парадокс Эйнштейна Подольского Розена" была опубликована в 1964 году, В ней Белл произвёл тщательный анализ доводов Эйнштейна, Подольского и Розена. Он убедительно показал, что теории со скрытыми переменными в принципе не позволяют объяснить результаты, полученные в реальных экспериментах. Белл пришёл к выводу:
"В квантовой теории с дополнительными параметрами для того, чтобы определить результаты индивидуальных измерений без того, чтобы изменить статистические предсказания, должен быть механизм, посредством которого настройка одного измеряющего устройства может влиять на чтение другого отдаленного инструмента. Кроме того, задействованный сигнал должен распространяться мгновенно …" [1].
Другими словами, если мы с позиции теории с дополнительными параметрами будем утверждать, что результаты измерений над каждой частицей полностью независимы друг от друга, независимы в физическом смысле, а все совпадения являются статистическими следствиями, то есть, по существу, они всего лишь случайные совпадения, то в этом случае мы будем вынуждены переложить весь груз этой случайности на некий механизм, упомянутый Беллом. Этот механизм должен обладать способностью подстраиваться под измерения со сверхсветовой скоростью. Следовательно, такая теория опять-таки противоречит специальной теории относительности и поэтому тоже отвергает ЭПР-аргументы.
Еще один запрет на сверхсветовую передачу классической информации накладывает теорема о запрете клонирования кубита. Клонирование могло бы позволить многократными измерениями клонов определить состояние телепортированного кубита.
Вместе с тем, вопрос о непосредственной передаче информации как таковой является до сих пор дискуссионным. В одной из работ этот вопрос формулируется в явном виде:
"Подразумевает ли передача нелокальной информации автоматически сверхсветовую сигнализацию?" [2, гл.1.1]
Здесь, как видим, фактически между квантовой (нелокальной) и классической информацией не проводится явной границы. Констатируется, что сама по себе передача сверхсветовой информации не приводит к возникновению парадоксов причинности, если эта информация недоступна. Квантовая информация, по крайней мере, в настоящее время таковой и является. Отсюда возникает интересная интерпретация нелокальной информации, как одной и той же информации одновременно присутствующей в двух разных областях пространства. Эта информация как бы объединяет эти области, она становится "пространственно расширенной" [2, гл.6.3].
Несмотря на все эти доводы, аргументы можно провести фундаментальную параллель между квантовой и классической информацией. Хотя носитель квантовой информации в явном виде, в эксперименте не зарегистрирован, есть гипотетическая возможность использования квантовой информации для сверхсветовой передачи информации классической.
Создание запутанных состояний гейтом
CNOT
Помимо косвенной сверхсветовой сигнализации посредством телепортации состояния запутанности можно рассмотреть еще один гипотетический способ непосредственной сверхсветовой коммуникации. С этой целью удобно использовать квантовые гейты CNOT, которые позволяют получить состояние запутанности вместо параметрического распада. Математическое описание этого процесса достаточно наглядно. Схема гейта CNOT представлена на рис.1a – изображение, чаще всего используемое в литературе, на рис.1б – изображение гейта, использованного в схеме традиционной квантовой телепортации (перевернуто).
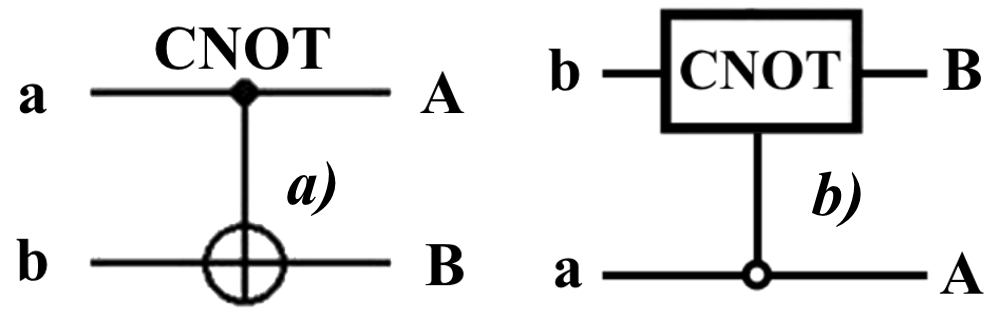
Рис.1. Схема гейта CNOT
Обозначения входов и выходов перевернутого изображения гейта, используемого далее в схеме рис.2, полностью соответствуют его традиционной таблице состояний (ниже). Математически этот квантовый оператор описывается выражением:
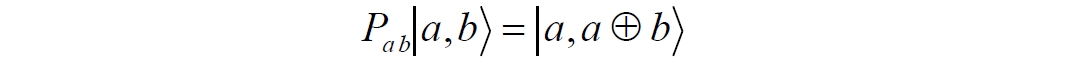
где a⊕b означает логическое сложение по модулю 2. Как видно из выражения, управляющий сигнал проходит со входа на выход без изменений. Матрица преобразования гейта CNOT имеет вид:
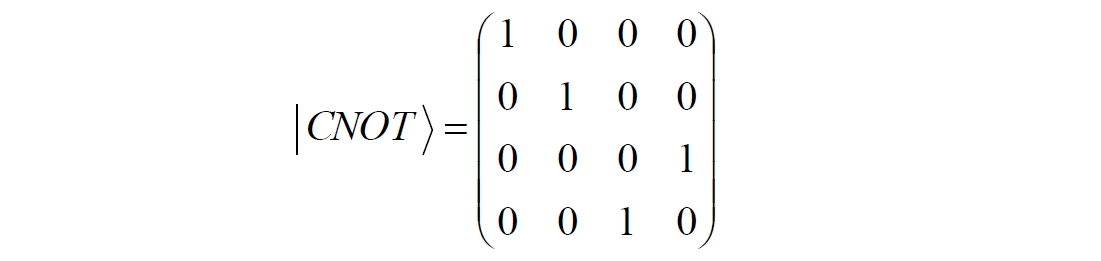
Подадим на управляющий и управляемый входы CNOT два фотона, соответственно, в следующих состояниях:
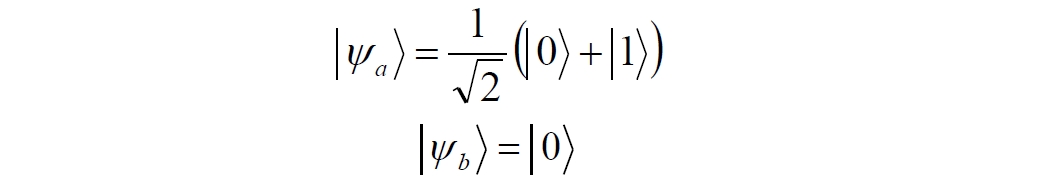
Это состояние системы фотонов на входе гейта будет описываться уравнением и матрицей вида:
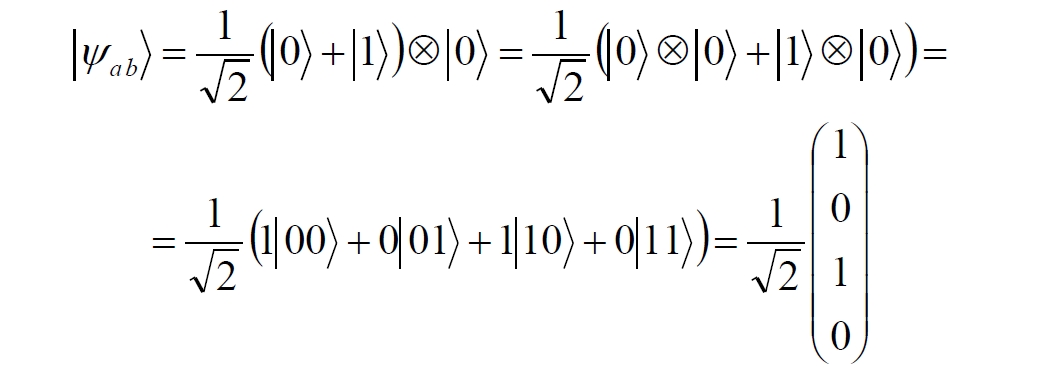
После прохождения фотонов через гейт будет получено новое состояние системы:
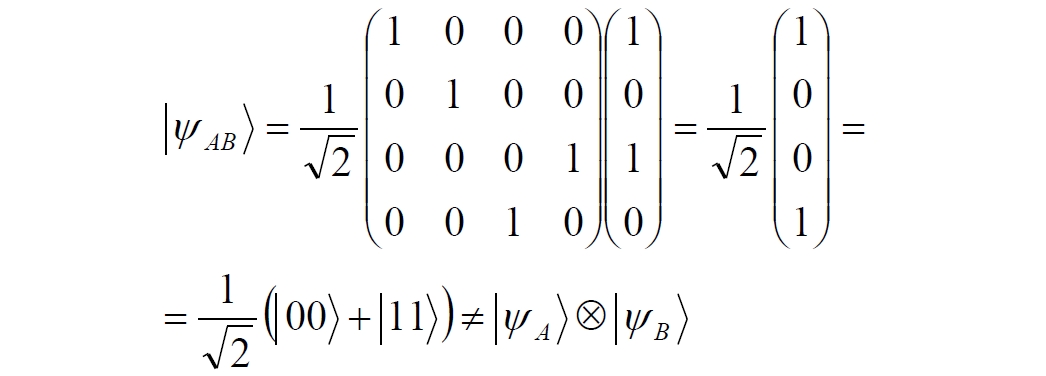
Знак неравенства означает, что на выходе получено запутанное (белловское) состояние фотонов: управляющего и управляемого, поскольку такое состояние не может быть факторизовано, то есть, не может быть представлено как тензорное произведение состояний независимых фотонов. Из этого сразу же следует, что входной управляющий сигнал на выход в неизменном виде все-таки не прошёл.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.