 полная версия
полная версияПравила счета элементов бесконечного множества
Точки любой линии на плоскости характеризуются двумя координатами. Точно так же и в рассмотренном примере все точки линии имеют две координаты, одна из которых просто равна нулю. Теперь становится ясным, почему мы обратили внимание на замечание "для простоты мы не берем". На самом деле в таком упрощении преследовалась цель упростить организацию подмены понятий. Ведь если у линии признать наличие имеющейся на самом деле второй координаты, то и для неё пришлось бы также формировать комбинированное число – индекс. Действительно, если вернуть в рассмотрение и стороны квадрата, то одна из них совпадет с отождествляемой линией. В этом случае надо было бы веско обосновать, почему координаты нижней стороны квадрата преобразуются в число z, а линия, полностью совпадающая с этой стороной, по-прежнему описывается одной координатой, хотя у неё однозначно имеется и вторая, нулевая?
Ясно, что разумные обоснования этого просто невозможны. Если же вернуть линии её законные права на вторую, нулевую координату, то все её собственные числа z будут начинаться с нулевого знака. То есть, с линией можно будет отождествить только одну единственную линию квадрата – его нижнюю сторону. Соответственно, мощность множества точек линии окажется меньше мощности точек квадрата в счетное число раз, то есть, в бесконечное. Мощность множества точек квадрата имеет более высокий порядок. Просто результат зависит от способа подсчета и может быть на любой вкус. Два способа мы уже увидели. Рассмотрим еще один.
Рассмотрим эти два объекта в единой метрической системе единиц, в которой размер точки квадрата равен размеру точки линии. Это естественное разумное предложение: бессмысленно приравнивать, скажем, два куска золота, размеры которых неизвестны. Длина стороны квадрата равна a, следовательно, метрически он содержит a2 точек. Отрезок по этой же причине содержит a метрических точек. Другим словами, квадрат и линия метрически тождественны. Тогда линия длиной na будет содержать заведомо больше точек, чем квадрат, если n > a.
Такой же результат можно получить и иначе. Возьмем тот же квадрат и разделим его на 4 части. Нижний ряд, два вновь образовавшихся квадрата назовём условно линией. Пока эти два квадрата, понятно, на линию не похожи.
Теперь разделим эти 4 квадрата ещё на 4 части каждый. Нижний ряд из 4 квадратов по-прежнему будем считать линией. Затем вновь каждый квадрат разделим крестом на 4 части. Теперь уже нижний ряд из 8 мелких квадратов отдаленно напоминает некую линию. Посчитаем, отношение количества этих квадратиков в исходном квадрате к их количеству на прообразе линии. По пройденным шагам деления эти отношения равны: 2, 4, 8. Легко обнаружить, что эти отношения будут возрастать по мере дальнейшего деления квадратов по уравнению 2n × 2n. Каждый из сомножителей означает, соответственно, деление по вертикали и по горизонтали. Продолжим такое же деление до бесконечности: n → ∞.
Очевидно, что все квадратики станут бесконечно малыми, превратятся в точки и исчезнут из видимости. При этом и линия станет тем, чем мы её обычно и представляем – линией с нулевой толщиной. Что важно, в этом случае и квадрат и линия состоят из одинаковых точек. И количества этих точек будут для квадрата – 2n × 2n, для линии – 2n. Отношение количеств или мощностей точек квадрата к точкам линии будет равно 2n. При увеличении числа шагов деления до бесконечности отношение также увеличится до бесконечности. Это значит, что мощность множества точек квадрата имеет более высокий порядок, чем мощность множества точек отрезка. Конечно, этот способ относится более к алгебре, чем к геометрии, но поэтому в нём и подмены с отождествлением скрыть труднее.
Наконец, можно рассмотреть и классический способ подсчета. Для этого возьмем одну из горизонтальных линий квадрата и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Поскольку координаты точек на отождествляемой линии совпадают с одноименными координатами линии квадрата, то будет пересчитывать одновременно и их: 1, 2, 3 и так далее. Очевидно, что мы получим два тождественных счетных множества. Вряд ли этому следует удивляться, физически и геометрически две линии тождественны. Следует отметить, что здесь мы пересчитываем не координаты, которые обозначаются действительными числами, необоснованно признанными несчетным множеством.
После завершения счета мы обнаруживаем, что одна единственная линия квадрата и отождествляемая с ним линия имеют равные мощности или количества точек. Но на квадрате таких линий – счетное множество (помним и отвергаем утверждение о несчётности действительных чисел). Следовательно, общее число точек на квадрате в счетное множество раз превышает число точек на любом его отрезке и отождествляемой линии.
Однако все рассмотренные отождествления, зависимые от способа счета, построены таким образом, что подсчет числа точек всегда приводит к результату либо большей, либо равной мощности множества точек квадрата по сравнению с множеством точек отрезка. Но можно подобрать и такое правило счета, что соотношение изменится на обратное: окажется, что число точек в отрезках является более мощным множеством. Для этого возьмем не один, а несколько одинаковых квадратов, просто выбрав в кубе несколько разных сечений, и одну линию с длиной ребра куба. Попробуем отожествить все точки этих квадратов с точками на линии. Вновь воспользуемся методикой нумерации точек, предложенной Кантором. Согласно ей, для того чтобы точки на квадратах можно было различить и из очевидных соображений мы обязаны признать, что квадраты имеют ещё одну координату. То есть, каждая точка квадрата в кубе в этом случае характеризуется тремя координатами:
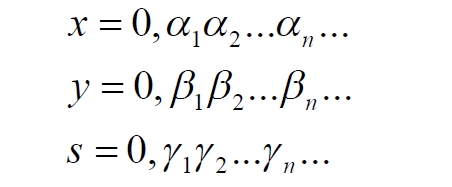
Для простоты, что, вообще-то, усложняет наше опровержение, ослабляет его, возьмём значения этих координат в кратчайшем виде, в виде единственной цифры от 0 до 9 без последующих дополнительных нулей, что во много раз увеличит число таких комбинированных точек, принадлежащих каждому квадрату. Для определенности возьмем в кубе 10 сечений, причем имеющие точное значение координаты s = 0; 0,1; 0,2 … 0,9. Теперь создадим по методу Кантора новые числа для точек каждого квадрата. Согласно этому методу каждая точка квадрата будет описываться новым числом – индексом. Исходные координаты задаём в следующем формате:
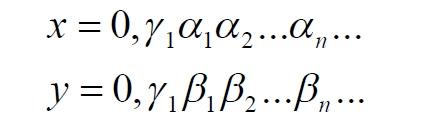
из которых формируем индекс:
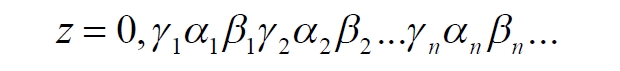
Здесь символом γ обозначен номер квадрата или, что то же самое, его координата в исходном кубе. Например, точки квадрата с номером s = 0,5 будут описываться индексом:
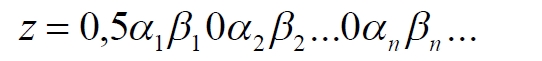
Как видим, закономерно и оправданно все точки и, соответственно, скомбинированные числа отличаются друг от друга, а все точки этого квадрата расположатся на интервале 0,5…0,6 отождествляемой линии и, более того, на линии останется бесконечное число точек, которым не будет соответствовать ни одна точка этого квадрата. Это точки, для которых индекс должен был бы содержать вместо нулей в позициях, кратных трём, другие цифры. Ничего не изменится, если цифру координаты s ставить в тройках последней.
Такая же ситуация будет наблюдаться с индексами и других девяти квадратов. Легко обнаружить, что комбинированные числа каждого квадрата изменяются в диапазонах, соответственно, [0, 0.1), [0.1, 0.2), [0.2, 0.3) и так далее. Таким образом, мы разместили все точки десяти квадратов на одной линии [0, 1]. Получается, что мощность множества, количество точек квадрата имеет меньший порядок, чем мощность множества точек любой линии. В нашем случае – в десять раз. Но мы могли использовать и другое количество квадратов. Тогда и их точки оказались бы во взаимном однозначном соответствии с точками части отрезка. В этом случае соотношение мощностей станет еще больше и даже, по желанию, в любое число раз.
Очевидно, что такой принцип "сколько будет? а сколько надо?", к которому, по сути, сводится метод Кантора, не может служить основой для корректного математического приема. Но в чем же состоит хитрость, изюминка, так сказать, канторовского метода отождествления? По какой загадочной причине происходит такое противоестественное отождествление? В чем его тайный механизм? Ведь мы же четко видим, что каждой точке квадрата можно однозначно привязать каждую точку линии, причем ни одна из точек не останется без своей единственной пары. А тайна, в сущности, предельно проста. Покажем это на еще одном несколько отвлеченном, но подобном примере.
Возьмем для лучшей визуализации квадрат с бесконечным числом точек в количестве… 1000х1000. Конечно, это на самом деле не бесконечность, но число все-таки очень большое – миллион точек, пересчитать которые вручную будет весьма непросто.
Выберем на этом квадрате одну линию, нижнюю грань квадрата. Согласно методу Кантора присвоим какой-то точке квадрата индекс:
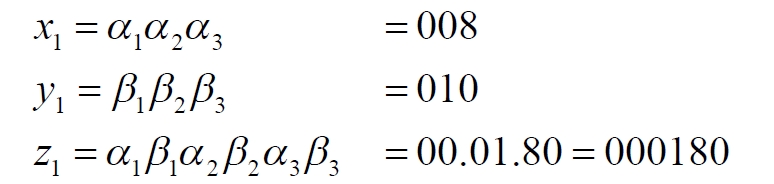
Здесь индекс z сначала представлен с разделительными точками, чтобы было видно, как он образован. Итак, мы получили число z, которое, видимо, точно имеется на отрезке [0, 999]. Правда, настораживает число нулей в этом индексе. Поэтому возьмем для уточнения другую точку на квадрате:
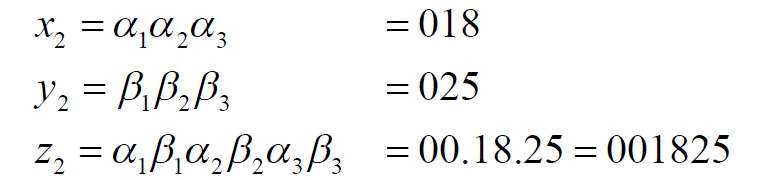
Что-то у нас, как видим, пошло не так. Сразу же можно сделать вывод: на линии [0, 999] такой точки точно нет. В чем же дело? Мы в точности следовали методу Кантора, просто используя отрезок не [0, 1], а более длинный [0, 999]. Принцип тот же, а размеры фигур явно не должны влиять на результат. Иначе получается противоречие: квадрат и линия размером [0, 1] тождественны по мощности, а квадрат и линия [0, 999] имеют уже разные мощности.
Однако именно в этом и состоит хитрость, а по сути подмена понятий в методе Кантора. В нашем случае мы можем попытаться решить проблему такой же дополнительной хитростью. Просто добавим в нашем индексе… запятую. В этом случае подозрительно большое количество нулей сразу превращается в нужное количество:
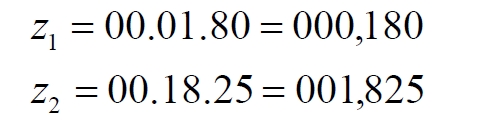
Вот теперь-то каждая из этих точек уже обязана найти своё соответствие на линии. Но возникает другое противоречие. Координаты всех точек квадрата и линии – целые натуральные числа. А здесь мы получили числа дробные, поэтому отождествлять эти индексы с точками линии мы не имеем права. Зато мы обнаруживаем ту самую загадку метода Кантора для отрезка [1, 0]. Фактически индекс формируется методом, схожим с умножением двух чисел. В нашем случае это соответствие должно выглядеть примерно так:
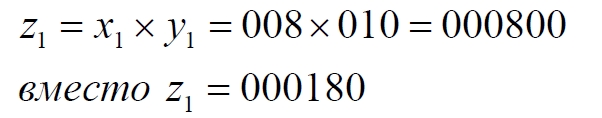
и для второго примера:
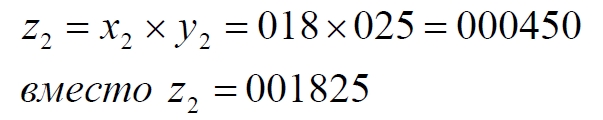
Для сравнения приведем и третий пример:
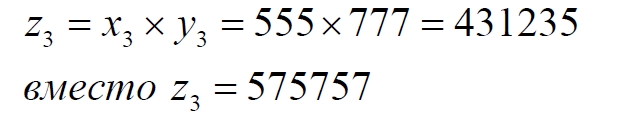
Как видим, оба метода – умножение и перетасовка цифр – дают числа одного и того же порядка с разрядностью площади квадрата (миллион). При этом можно догадаться, что количество разных произведений координат ровно в два раза меньше, чем количество пар сомножителей, поскольку они могут меняться местами. Действительно, пар сомножителей ровно миллион, следовательно, и произведений тоже ровно миллион. Поскольку существуют симметричные пары сомножителей, то их произведения равны. Следовательно, число уникальных произведений равно полумиллиону. Мы полагаем, что произведение разных чисел дают разные результаты.
При перетасовках цифр смешиваемых пар также ровно миллион, следовательно, и результирующих чисел с перетасованными цифрами также будет миллион. Но в этом случае, что довольно странно, среди них не будет одинаковых. Иначе говоря, при умножении пар какие-то значения в ряду из миллиона чисел будут отсутствовать. Это легко обнаружить: при перетасовке пар может быть получено число 999 999, но при умножении пар такое число получено быть не может – максимальное значение произведения равно 998 001. И таких "отсутствующих" произведений пар – ровно полмиллиона.
Несомненная выгода метода Кантора в том, что каждая точка получит свой индивидуальный, уникальный индекс. Однако остаётся проблема: таких индексов заведомо больше, чем элементов в строке, следовательно, и в отождествляемой линии. Искусственно введенная запятая сжимает эти числа до интервала отрезка [0, 999], но множество из них сразу же становятся дробными, то есть, объективно также не могут этому отрезку принадлежать. Увеличение до бесконечности дискретности квадрата и линии сохранит эту тенденцию без отождествления точек квадрата и линии.
А что же с исходным методом Кантора для единичного отрезка? Там, как видим, произведена точно такая же замена умножения двух чисел на перетасовку их цифр, позволившая получить нужное количество индексов. Порядок чисел при умножении и перетасовке по-прежнему один и тот же. Однако индексы или произведения координат имеют больший порядок дискретности, чем каждая из координат, в том числе, и точки отождествляемой линии. И здесь происходит всё та же подмена понятий при подсчете числа элементов в ряду, что и при подсчете числа четных чисел в натуральном ряду. Только здесь каждой точке линии соответствует бесконечное число индексов точек квадрата. И вот почему.
Понятно, что в числах с бесконечным числом знаков разглядеть это весьма непросто, тем более что все они выглядят одинаково, поскольку одинаково начинаются – с нуля и запятой после него. Сравнивая числа – координату линии (q) и координатный индекс z(x, y), например, для q=x=y=0,1 (точное значение), мы находим z=0,11. Дискретность z в этом случае в 10 раз выше, чем дискретность q. То есть, между двумя дискретными значениями q=0,1…0,2 поместится десять подобных индексов. Если q=x=y=0,12345, то z=0,1122334455 и дискретность z уже в 100000 раз больше дискретности q. Следовательно, между точками q=0,11223…0,11224 (это точные значения) поместится 100000 индексов с дискретностью z. Другими словами, беря две координаты с некоторой дискретностью (числом знаков после запятой), мы получаем индекс с удвоенной дискретностью и степенным увеличением их количества. Сравнивая координаты линии и индексы, мы сравниваем фактически не их значения, которые предельно скрыты от нас и не могут быть равны, а их порядковые номера, которые для счетных множеств, разумеется, всегда найдут соответствие.
Описать этот процесс однозначно и максимально развернуто крайне сложно. Поэтому рассмотрим ещё один пример. Пусть отрезок [0, 1] состоит из миллиарда (109) точек, а соответствующий ему квадрат, следовательно, содержит 1018 точек. Эти числа являются так же и количествами их порядковых номеров, эквивалентами мощностей этих множеств. Сразу же обнаруживаем, что на линии точек меньше, чем в квадрате. Если постоянно удваивать количество точек вплоть до бесконечности, это отношение будет только возрастать.
Если для отождествления мы возьмём произвольную точку указанного квадрата, то её координатный индекс будет содержать 1018 знаков после запятой. И мы не имеем никакого права отождествлять этот индекс с точкой на линии, поскольку на ней допустимы только числа с 109 знаков после запятой, точек с такой дискретностью на линии просто нет. При увеличении дискретности квадрата и линии это расхождение будет расти по квадратичному закону.
Кстати, здесь мы наглядно обнаруживаем абсурдность сравнивания количества чисел натурального ряда и его части. Мы можем диагональным процессом Кантора тривиально перенумеровать точки линии и точки квадрата, даже не формируя для них индексы, и получим при этом равенство их количества. Однако мы только что увидели, что такое равенство противоречиво, а попросту его нет. Следовательно, и сравнивание количества членов множеств путем их раздельного пересчитывания – это опасный, ошибочный, некорректный метод, позволяющий получить любой желаемый результат, и которым следует пользоваться предельно продуманно.
Действительно, мы можем сравнивать точки линии и точки квадрата таким же простым раздельным пересчетом, получив в обоих случаях бесконечность. Но это разные бесконечности, бесконечности разной мощности. Напротив, возьмем какую-либо y-линию на квадрате и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Одновременно с этими точками будем пересчитывать и точки на линии: 1, 2, 3 и так далее. Мы тем самым однозначно отождествим все точки линии со всеми точками на одной из линий квадрата. Остальные линии квадрата, с другими координатами, разумеется, останутся без номеров. Это самый правильный способ пересчета и отождествления.
Итак, даже при ослаблении нашей аргументации мы приходим к выводу, который противоречит выводу Кантора об их равенстве. Два способа нумерации, основанных тождественно на одном и том же методе, приводят к несовместимым, противоположным выводам. Поэтому этот метод Кантора логически неверен, ошибочен. И вновь возникает риторический вопрос, какой же в этом случае метод верный? Методов группировки может быть сколько угодно, поэтому верным является только один метод – без группировки, то есть, сравнивать можно только равнозначные объекты – линию с линией. В этом случае вывод однозначный – множества точек линии и квадрата не равномощны. Самым простым и наглядным способом определения этого является простое наложение линии на квадрат и отождествление соприкоснувшихся точек.
Практически такая же противоречивая ситуация возникает и при отождествлении двух противоположных сторон квадрата: верхней и нижней, либо любых двух средних линий квадрата. Возникает совершенно противоестественная ситуации: эти пары линий вообще нельзя отождествить, поскольку нумерация их точек не имеет одинаковых значений. Верхняя сторона квадрата должна иметь по Кантору значения первой цифры после запятой всех точек, начинающиеся с 9, а нижняя – с 0, а средние, например, с 3 и 5. Две явно одинаковые линии оказываются несопоставимыми.
Стереографическая проекция
В заключение отметим, что один из истоков или примеров отождествления бесконечностей разной мощности можно обнаружить в механизме стереографической проекции, также фактически отождествляющей точку и отрезок. Рассмотрим соотношение между размерами двух отрезков, которые затем сожмем в точки:
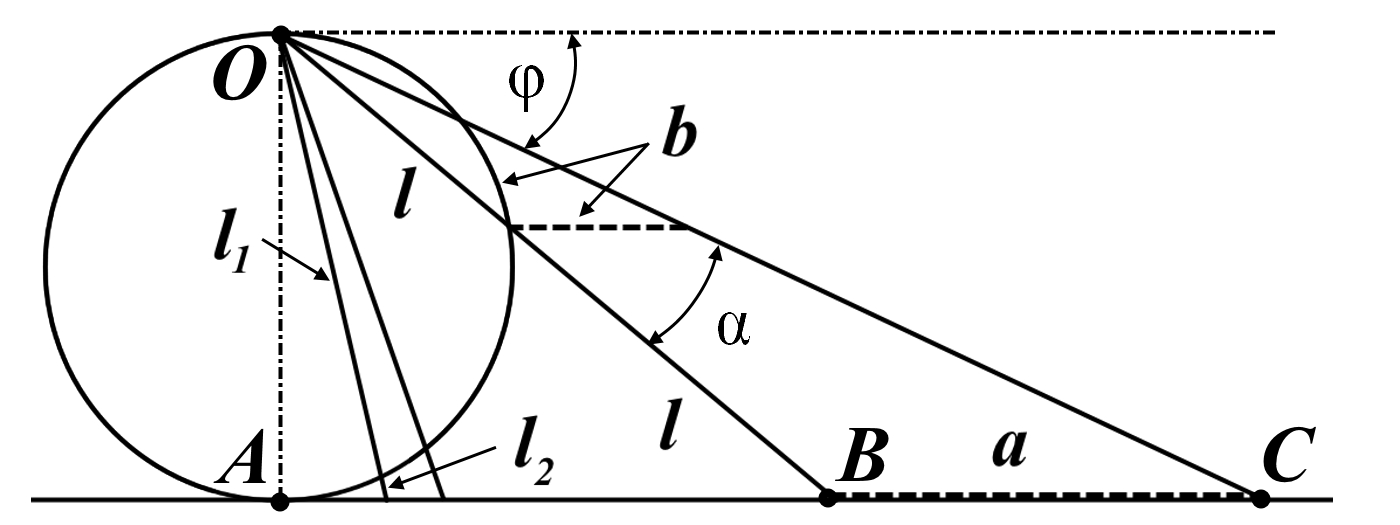
Рис.3. Стереографическая проекция отождествляет отрезок и точку
Мы не описываем сущность стереографической проекции, её описание можно найти в литературе. Каждая проекционная линия, прямая делится проецируемой точкой окружности между полюсом и проекционной плоскостью на две части, например, l1 и l2. Возьмем частный случай, когда отрезок делится пополам, то есть, l1 = l2 = l. Проведем ещё одну проекционную линию под углом α к исходной линии. В этом случае на окружности образуется дуга, а на плоскости – отрезок. Проведем из проецируемой точки пересечения дополнительный отрезок между проекционными лучами параллельно плоскости из проецируемой точки. Обозначим полученный отрезок через b, а проекцию на плоскости – через a. Из подобия треугольников следует, что
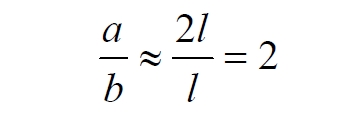
Здесь знак неточного равенства взят из предположения, что отрезок b приблизительно равен длине дуги. Это не точное равенство, но в средней части окружности отрезок и дуга отличаются друг от друга незначительно, в конечное число раз. Теперь найдем предел этого отношения, когда угол между двумя проецирующими прямыми стремится к нулю:
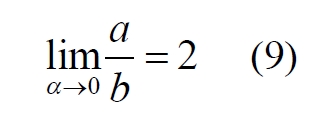
Это очевидный и аналитически достоверный предел. Но при этом возникает вопрос: что же означает это отношение 2? Две проекционные прямые слились в одну, и эта прямая пересекает и окружность и плоскость в одной точке каждую. Что же означает это соотношение для двух разных точек? Если считать, что точка – это то, что не имеет частей, то ответ становится совершенно туманным. Выходит, что точки не имеют частей, но в разном количестве. В любом случае для утверждения, что точка на окружности спроектировалась в единственную тождественную точку на плоскости, четких, бесспорных оснований уже нет.
Однако это соотношение мы нашли для конкретного, среднего угла. А что если пару прямых, проектирующих лучей повернуть ближе к горизонтальному направлению? То есть, устремить к нулю не только угол между проецирующими прямыми, но и их средний угол к плоскости. В этом случае мы увидим, что отношение будет стремиться к бесконечности:
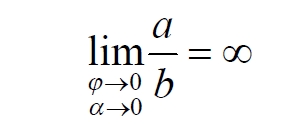
Вопрос о смысле этого отношения становится еще более острым. Если две точки – исходная, проецируемая и её проекция – отождествляются, тогда что означает это отношение? Изначально оно составлялось как отношение длины проецируемого отрезка и проекции, которые в дальнейшем уменьшением угла до нуля были преобразованы в точки. Хотя точка и не имеет частей, но величина соотношения определенно выглядит как количество проецируемых точек в проекции. Звучит весьма странно: проецирующий луч создаёт проекцию, имеющую явно не нулевые, не точечные размеры. Можно сколько угодно с этим не соглашаться, но как можно иначе рационально объяснить это соотношение?
Обычно бесконечно малые величины в алгебре характеризуются параметром порядка малости. Если две величины имею отношение конечной величины, то они считаются величинами одного порядка малости. Если отношение стремится к бесконечности, то величины имеют разный порядок малости. С учетом этого следует предположить, что стереографическая проекция окружности на плоскость некорректна, а проекциями её точек фактически являются плоские фигуры, отрезки.
Рассмотрим эту же ситуацию с другой точки зрения, не отождествляя дугу окружности и прямой отрезок. Для этого нам понадобится следующее интересное соотношение, теорема. Если к отрезку дуги провести по два луча из центра окружности (рис.4) и из любой точки окружности, кроме точек этой дуги, то угол между лучами в первом случае будет в два раза больше угла между лучами во втором случае. Приведем краткое доказательство этой теоремы.
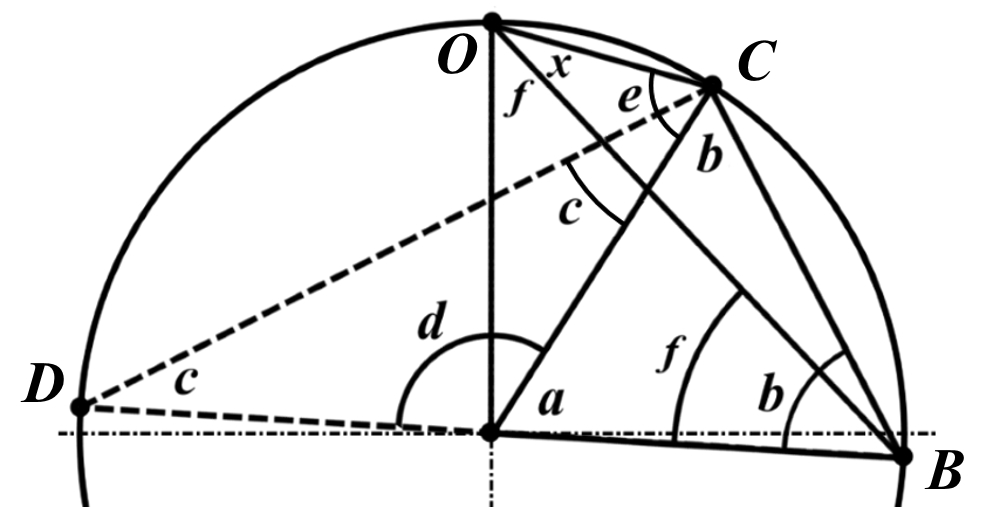
Рис.4. Теорема об углах на дуге окружности
Итак, возьмем на окружности рис.4 некоторую произвольную дугу CB и проведем к ней две пары лучей – из центра и из полюса О. Проведем далее вспомогательный диаметр BD и линию CD. Обозначим одинаковыми буквами равные углы в равносторонних треугольниках у равных сторон. По условиям задачи нам задан некий центральный угол a. Докажем, что а = 2x. Из построений на рисунке видим:
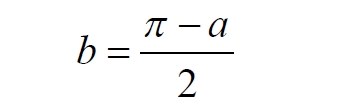
Угол при вершине штрихового треугольника:
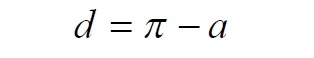
Углы при основании равностороннего треугольника.
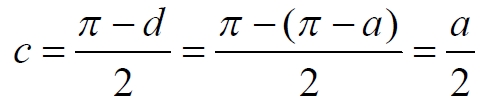
Углы при основании равностороннего треугольника с искомым углом:
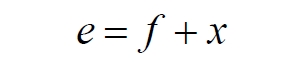
Составляем баланс углов в треугольнике с искомым углом x:
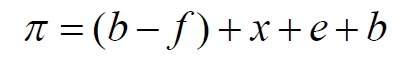
Подставляем условно известное значение угла f:
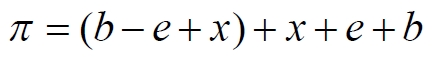
Раскрываем скобки
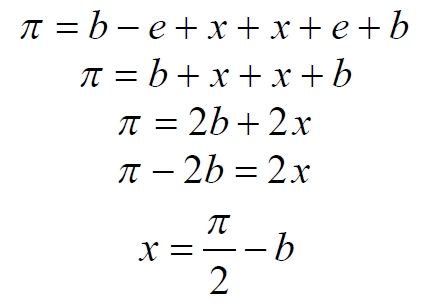
Подставляем значение заданного угла а