Расчеты конструктору

Выбираем меньшее значение момента инерции « j min ».

.rm=sqrt(j min/s)… Радиус инерции минимальный.

Контрольный расчет:

Прямоугольная труба.

Высота = 80;

Высота отв.= 60;

Ширина = 60..

Ширина отв.= 40..

S=2400; Jxx =1840000; Wxх= 46000.. Jyy =1120000; Wyy= 37333,(3)..

.i=21,60246899… Диагональ = 100..

Расчет параметров сечения треугольника.

Сечение – Треугольник.

Высота треугольника h.

Основание треугольника b.

Центр тяжести ЦТ. От основания до ЦТ размер Z.

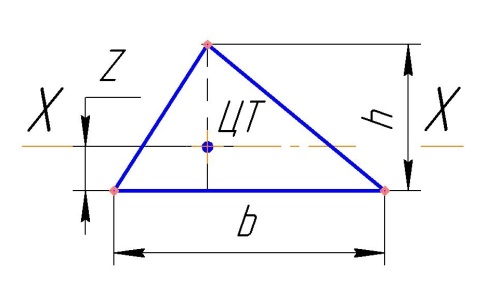
Расчет:

Sk=(h*b)/2… Площадь сечения.

Jxk=b*h*h*h/36… Момент инерции по оси Х-Х.

Для волокна вершины треугольника:

Mik=Jxk/(h*2/3)… Момент сопротивления изгибу по оси Х-Х.

Для волокна основания треугольника:

Mio=Jxk/(h*1/3)… Момент сопротивления изгибу по оси Х-Х.

Rk=sqrt(Jxk/Sk)… Радиус инерции сечения.

Z=h/3… Высота Ц.Т. от основания.

Контрольный расчет:

Треугольное сечение: Высота=80; Основание=60;

S=2400; Z =26,6(6); от подошвы до центра тяжести..

Jxx =853333,3(3); Wxn=32000,0; для нижних волокон..

Wxv=16000,0; … для верхних волокон..

.i=18,85618083..

Расчет параметров сечения тавра.

Сечение – Тавр.

Высота пера h.

Толщина пера b.

Высота подошвы hm.

Ширина подошвы bm.

Центр тяжести ЦТ. От подошвы до ЦТ расстояние xc.

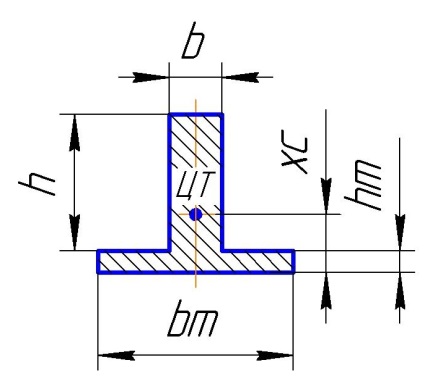
Контрольный расчет:

Тавровое сечение:

Высота ребра = 80.. Толщина ребра =20..

Ширина подошвы = 60.. Толщина подошвы = 40..

Площадь S=4000.;

XC=44,0..; от подошвы до центра тяжести..

Jxx =4629333,(3)..

Х-Х – параллельна подошве..

Wxx=60912,28070175;.. минимальное..

Jyy=773333,(3)..;

Wyy=25777,(7);..

Радиус инерции .i= 13,90444.. минимальное..

…….

Расчет:

.s=(h*b)+(hm*bm)… Площадь сечения тавра.

.j1=b*h*h*h/12… Момент инерции пера относительно Ц.Т. пера.

.j2=bm*hm*hm*hm/12… Момент инерции подошвы относительно Ц.Т. подошвы.

.f1=h*b… Площадь пера.

.f2=hm*bm… Площадь подошвы.

.x1=(h/2)+hm…

.x2=hm/2… Gsf = 461030/2725231222…

Центр тяжести тавра от низа подошвы « xc ».

.xc=((f1*x1)+(f2*x2))/(f1+f2)…

.r1=(((h/2)+hm)-xc)… Радиус ц.т. пера от ц.т. тавра.

.r2=xc-(hm/2)… Радиус ц.т. подошвы от ц.т. тавра.

.jx1=j1+(r1*r1*f1)… Момент инерции смещенного пера.

.jx2=j2+(r2*r2*f2)… Момент инерции смещенной подошвы.

.jx=jx1+jx2… Момент инерции тавра по Х.

.wx=jx/((h+hm)-xc)… Момент сопротивления изгибу тавра по Х.

.jy1=h*b*b*b/12…

.jy2=hm*bm*bm*bm/12…

.jy=jy1+jy2… Момент инерции тавра по Y.

.wy=jy/(bm/2)… Момент сопротивления изгибу тавра по YY.

Выбираем меньшее значение момента инерции « j min ».

.rm=sqrt(j min/s)… Радиус инерции минимальный.

Расчет параметров сечения рельса.

Высота головки = h.

Ширина головки = b.

Высота стенки = hs.

Толщина стенки = bs.

Ширина подошвы = bm.

Толщина подошвы = hm.8888

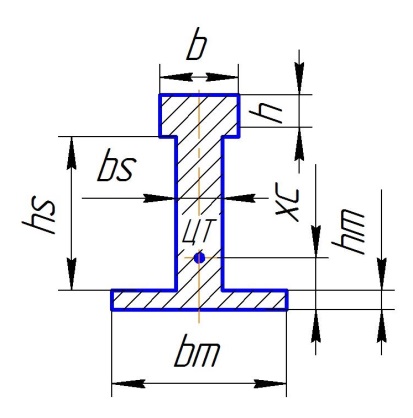
Контрольный расчет:

Сечение типа Рельс:

Высота головки = 40..

Ширина головки =60..

Высота ребра = 80..

Толщина ребра =20..

Ширина подошвы = 100..

Толщина подошвы = 10..

S=5000.;

XC =69,80..; от подошвы до центра тяжести..

Jxx =9886466,(6)..

Х-Х – параллельна подошве..

Wxx=141639,923591;.. минимальное..

Jyy=1606666,(6)..

Wyy=32133,(3);..

.i= 17,925773.. минимальное..

……

Расчет:

.s=(h*b)+(hm*bm)+(hs*bs)… Площадь сечения рельса.

.j1=b*h*h*h/12… Момент инерции головки относительно собственного Ц.Т.

.j2=bs*hs*hs*hs/12 … Момент инерции стенки относительно собственного Ц.Т.

.j3=bm*hm*hm*hm/12… Момент инерции подошвы относительно собственного Ц.Т.

.f1=h*b … Площадь головки.

.f2=hs*bs … Площадь стенки.

.f3=hm*bm… Площадь подошвы.

.x1=(h/2)+hs+hm …

.x2=(hs/2)+hm…

.x3=hm/2…

Центр тяжести рельса от подошвы « xc ».

.xc=((f1*x1)+(f2*x2)+(f3*x3))/(f1+f2+f3)…

.r1=((h+hs+hm)-h/2)-xc… Радиус ц.т. головки от ц.т. рельса.

.r2=((hs/2)+hm)-xc… Радиус ц.т. стенки от ц.т. рельса.

.r3=xc-(hm/2)… Радиус ц.т. подошвы от ц.т. рельса.

.jx1=j1+(r1*r1*f1)… Момент инерции смещенной головки.

.jx2=j2+(r2*r2*f2)… Момент инерции смещенной стенки.

.jx3=j3+(r3*r3*f3)… Момент инерции смещенной подошвы.

.jx=jx1+jx2+jx3… Момент инерции рельса по ХХ.

.wx1=jx/((h+hs+hm)-xc)… Момент сопротивления изгибу рельса по ХХ.

.wx=jx/xc… Момент сопротивления изгибу рельса по ХХ.

Берем меньшее значение W из двух значений…

.jy1=h*b*b*b/12…

.jy2=hm*bm*bm*bm/12…

.jy3=hs*bs*bs*bs/12…

.jy=jy1+jy2+jy3… Момент инерции рельса по Y.

Выбор максимально удаленной части для оси Y-Y.

.wy=jy/(b/2)… Момент сопротивления изгибу рельса по YY.

.wy=jy/(bm/2)… Момент сопротивления изгибу рельса по YY.

Берем меньшее значение W из двух значений…

Выбираем меньшее значение момента инерции « j ».

.rm=sqrt(jx/s)…

.rm=sqrt(jy/s)…

Расчет параметров сечения трапеции.

Высота трапеции = h.

Верх трапеции = a.

Основание трапеции = b.

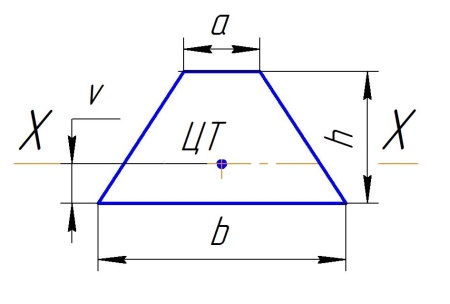
# Ведем расчет по классическим формулам 14-03-2020 г..

Pii = 3,141592654… Число Пи.

.x=(b-a)/2..

.y=(h*h)+(x*x)..

.ab=sqrt(y).. # Извлекаем квадратный корень ( Боковая грань трапеции ).

.xx=((a+x)*(a+x))+(h*h)..

.dt=sqrt(xx).. # Извлекаем квадратный корень (Диагональ трапеции ).

Ugrx=h/x..

Ugr=arctan(Ugrx).. # АрксТангенс от Ugrx в радианах.

Ug=Ugr*180/Pii.. # Угол в градусах…( Угол при основании ).

.s=h*(b+a)/2.. Площадь трапеции.

Далее расчет по оси Х-Х ( Ось Х-Х параллельна основанию ).

Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jp=h*h*h*a/12.. # Момент инерции прямоугольника.

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.x=(b-a)/2.. # Основание одного треугольника.

Jt=h*h*h*x/36.. # Момент инерции одного треугольника.

.yt=h/3.. # Нейтральная ось от основания треугольника.

# Центр тяжести системы от основания ( нейтральная ось ).

.z=(((St+St)*yt)+(Sp*h/2))/(St+St+Sp).. ( На рисунке z обозначена как V ).

# Момент инерции двух треугольников со смещенным центром.

.at=z-yt.. # Смещение центра тяжести треугольников относительно Ц.Т. трапеции.

Момент инерции двух треугольников по Х-Х со смещенным центром.

Jts=2*(Jt+at*at*(St))..

# Момент инерции прямоугольника по Х-Х со смещенным центром.

.ap=z-(h/2).. # Смещение центра прямоугольника относительно Ц.Т. трапеции.

Jps=Jp+ap*ap*Sp.. Момент инерции прямоугольника по Х-Х со смещенным центром.

.jx=Jps+Jts.. # Момент инерции трапеции по оси ХХ.

.v=z.. # От основания – до нейтральной оси трапеции.

.wxv=jx/(h-v).. # Момент сопротивления изгибу для верхнего основания X-X.

.wxn=jx/v.. # Момент сопротивления изгибу для нижнего основания X-X.

.xr=jx/(Sp+St+St).. # jx / Площадь трапеции.

Rix=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции ).

Далее расчет по оси YY.

# Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jpy=a*a*a*h/12.. # Момент инерции прямоугольника.

# …

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.hy=(b-a)/2.. # Высота одного треугольника.

Jty=hy*hy*hy*h/36.. # Момент инерции одного треугольника Y-Y.

.yty=hy/3.. # Нейтральная ось от основания треугольника.

.ytyc=yty+(a/2).. # Нейтральная ось треугольника от оси Y-Y.

# Момент инерции двух треугольников со смещенным центром.

# .ytyc – Смещение центра треугольников от оси Y-Y.

Jtsy – Момент инерции двух треугольников по Y-Y со смещенным центром.

Jtsy=2*(Jty+ytyc*ytyc*(St))..

# Jpy – Момент инерции прямоугольника ( смещения нет ).

.jyy=Jpy+Jtsy.. # Момент инерции трапеции по оси Y-Y.

.wyv=jyy/(b/2).. # Момент сопротивления изгибу для Y-Y.

.xr=jyy/(Sp+St+St).. # ( jx / Площадь трапеции ).

Riy=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции по Y-Y ).

Контрольный расчет:

Сечение в виде симметричной трапеции.

Высота трапеции = 30.

Основание трапеции = 50.

Верх трапеции = 20.

…

Боковая грань трапеции = 33.54102.

Диагональ трапеции = 46.097722.

Угол при основании = 63.434949 Градус.

Площадь трапеции = 1050.0.

Далее расчет по оси Х-Х.

Момент инерции по Х-Х одного треугольника Jt = 11250.0.

Центр тяжести системы Х-Х от основания = 12.8571.

Момент инерции двух треугольников по Х-Х со смещенным центром. = 26173.4694.

Момент инерции прямоугольника по Х-Х со смещенным центром. = 47755.102.

Момент инерции трапеции по оси ХХ. = 73928.5714.

Момент сопрот.изгибу по оси ХХ. = 4312.5 верх; 5750.0 низ;

Радиус инерции оси Х-Х = 8.391..

Далее расчет по оси YY.

Момент инерции по Y-Y одного треугольника Jt = 2812.5..

Момент инерции двух треугольников по Y-Y со смещенным центром. = 106875.0..

Момент инерции прямоугольника по оси Y-Y ( смещения нет ) = 20000.0..

Момент инерции трапеции по оси Y-Y. = 126875.0..

Момент сопрот.изгибу по оси Y-Y. = 5075.0..

Радиус инерции оси Y-Y = 10.9924..

Расчет параметров сечения шестигранника.

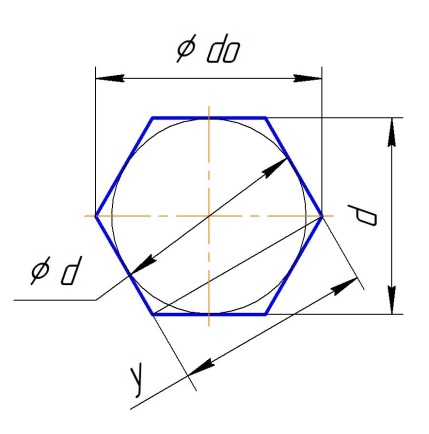
Ось ХХ проходит через вершины на описанном диаметре do.

.d – Вписанный диаметр ( размер под ключ ).

.ss=0,866025403*d*d … Площадь шестигранника через вписанный диаметр.

.do=1,154700538*d … Описанный диаметр.

.ss=0,6495190528*do*do … Площадь шестигранника через описанный диаметр.

.ls=do/2 … Длина грани.

Для дальнейшего расчета представим шестигранник.

Как две трапеции соединенные основаниями.

Далее расчет заимствуем из расчета трапеции.

.h=d/2 … Высота трапеции.

.a=do/2… Верх трапеции ( Длина грани ).

.b=do… Основание трапеции.

Далее расчет трапеции:

.s=h*(b+a)/2.. Площадь трапеции.

Далее расчет по оси Х-Х ( Ось Х-Х параллельна основанию )..

Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jp=h*h*h*a/12.. # Момент инерции прямоугольника.

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.x=(b-a)/2.. # Основание одного треугольника.

Jt=h*h*h*x/36.. # Момент инерции одного треугольника.

.yt=h/3.. # Нейтральная ось от основания треугольника.

# Центр тяжести системы ( трапеции ) от основания ( нейтральная ось )..

.z=(((St+St)*yt)+(Sp*h/2))/(St+St+Sp).. ( На рисунке z обозначена как V ).

# Момент инерции двух треугольников со смещенным центром.

.at=z-yt.. # Смещение центра тяжести треугольников относительно Ц.Т. трапеции.

Момент инерции двух треугольников по Х-Х со смещенным центром.

Jts=2*(Jt+at*at*(St))..

# Момент инерции прямоугольника по Х-Х со смещенным центром.

.ap=z-(h/2).. # Смещение центра прямоугольника относительно Ц.Т. трапеции.

Jps=Jp+ap*ap*Sp.. Момент инерции прямоугольника по Х-Х со смещенным центром.

.jx=Jps+Jts.. # Момент инерции трапеции по оси ХХ.

Ось ХХ трапеции смещена относительно оси ХХ шестигранника на величину V или z.

Jtz – Момент инерции трапеции по оси смещенной на величину V.

Jtz= jx + V*V*s..

Jse= Jtz+ Jtz.. Момент инерции шестигранника по оси ХХ.

Wse=Jse*2/d.. Момент сопротивления изгибу шестигранника по оси ХХ.

.rm=sqrt(Jse/(s+s))… Радиус инерции оси Х-Х.

..... .....

Контрольные цифры:

Вписанный диаметр ( размер под ключ ) d = 86,60254038..

Описанный диаметр do = 100..

Площадь шестигранника = 6495,190528..

Расчет параметров произвольного сечения.

Заданное произвольное сечение представим как набор элементарных прямоугольников.

Ось Х-Х расположим по нижней стороне первого прямоугольника.

Определяем площадь, расстояние центра тяжести от оси Х-Х и

момент инерции первого прямоугольника.

Определяем площадь, расстояние центра тяжести от оси Х-Х и

момент инерции второго прямоугольника.

Находим расстояние центра тяжести системы двух прямоугольников от оси Х-Х.

Находим момент инерции каждого прямоугольника относительно оси

проходящей через общий центр тяжести.

Находим общий для системы момент инерции и общую площадь.

Рассчитанную систему принимаем как первый прямоугольник.

Добавляем еще один прямоугольник и повторяем выше приведенный расчет.

Этот цикл расчетов ведем, пока не просчитаем все прямоугольники произвольного сечения.

Высота первого прямоугольника = h.

Ширина первого прямоугольника = b.

.j1=b*h*h*h/12… Момент инерции первого прямоугольника.

.w1=j1/(h/2)… Момент сопротивления первого прямоугольника.

.s1=h*b… Площадь сечения первого прямоугольника.

.xc1=h/2… Высота центра тяжести первого прямоугольника от оси Х-Х.

.m1=s1*(h/2)… Момент площади первого прямоугольника относительно оси Х-Х.

# Точка расчета № 1…

Высота второго прямоугольника = h1.

Ширина второго прямоугольника = b1.

Высота расположения основания

второго прямоугольника относительно оси Х-Х = hx.

.j2=b1*h1*h1*h1/12… Момент инерции второго прямоугольника.

.w2=j2/(h1/2)… Момент сопротивления второго прямоугольника.

.s2=h1*b1… Площадь сечения второго прямоугольника.

.xc2=(h1/2)+hx… Высота центра тяжести второго прямоугольника от оси Х-Х.

.m2=s2*((h1/2)+hx)… Момент площади второго прямоугольника относительно оси Х-Х.

.xx=(m1+m2)/(s1+s2)… Расстояние Ц.Т. от оси Х-Х системы двух прямоугольников.

R1=xx-xc1… Расстояние между Ц.Т. системы и Ц.Т. первого прямоугольника.

R2=xc2-xx… Расстояние между Ц.Т. системы и Ц.Т. второго прямоугольника.

.j1x=j1+( R1*R1*s1)…Момент инерции первого прямоугольника относительно Ц.Т. системы.

.J2x=j1+( R2*R2*s2)…Момент инерции второго прямоугольника относительно Ц.Т. системы.

.Jx=j1x+j2x… Момент инерции системы двух прямоугольников относительно Ц.Т. системы.

Sx=s1+s2… Суммарная площадь двух прямоугольников.

.... .....

Далее в расчете принимаем систему двух прямоугольников за новый, первый прямоугольник у которого:

.s1=Sx… xc1=xx… j1=Jx… m1=Sx*xx…

Вводим данные следующего прямоугольника:

( считая его новым вторым прямоугольником ) и снова проходим весь расчет,

начиная с # Точки расчета № 1…

Для проверки можно пересчитать сечение « Рельс ».

……..

Кстати все вышеизложенные расчеты эффективнее выполнять используя программы.

Программы можно скопировать из книги « Python 3 Полезные программы книга третья. ».

Программы значительно экономят время и уменьшают вероятность ошибок в расчетах..

Программы можно выполнить так же в Excel.

,,,,

Разные расчеты элементов деталей машин.

Расчет параметров профиля звездочки по ГОСТ 591-69.

Для примера построения принимаем нестандартные исходные данные:

Число зубьев звездочки = 5..

Шаг цепи = 50 …

Диаметр ролика цепи = 36 ..

…… …….. …….

Расчет лучше производить по программе.

В программе использовать формулы из ГОСТ 591-69..

….

Построение профиля зуба проводим в следующем порядке:

Строим диаметр окружности выступов de = 98,819..

Строим диаметр делительной окружности dd = 85,065..

От вертикальной осевой вправо и влево откладываем размеры по = 0,5 е.

Е = 1,5 .. 0,5 е = 0,75 .. Проводим вспомогательные осевые параллельные вертикальной осевой.

Левая вспомогательная осевая при пересечении с делительной окружностью создает точку « О ».

Из этой точки проводим радиус впадины R = 18,14 …

Через точку « О » проводим прямую перпендикулярную вертикальной осевой.

От этой прямой отмеряем размер « Y 2 » вниз и « Y 1 » вверх от прямой.

От левой вспомогательной осевой влево отложим размер « Х 2 ». Пересечение линий « Y 2 » и « Х 2 » даст центр радиуса R 2 = 26,178 – радиуса головки зуба ( центр – точка « О2 » ). Пересечение линий « Y 1 » и

« Х 1 » даст центр радиуса R 1 = 46,94 – радиуса сопряжения радиусов R и R 2 ( центр – точка « О1 » ). Точки сопряжения находятся на прямых линиях проходящих через точки центров сопрягаемых радиусов. ( точки « Е » и « F » ). Из центра окружностей проводим луч с отклонением на половину углового шага зубьев звездочки. При заданном числе зубьев = 5 .. отклонение = 36 градусов. Построенная часть зуба симметрична относительно этого луча.

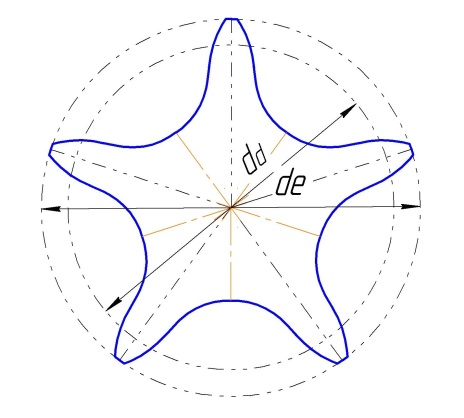
Исходные данные:

Число зубьев звездочки z = 5..

Шаг цепи t = 50 …

Диаметр ролика цепи d = 36 ..

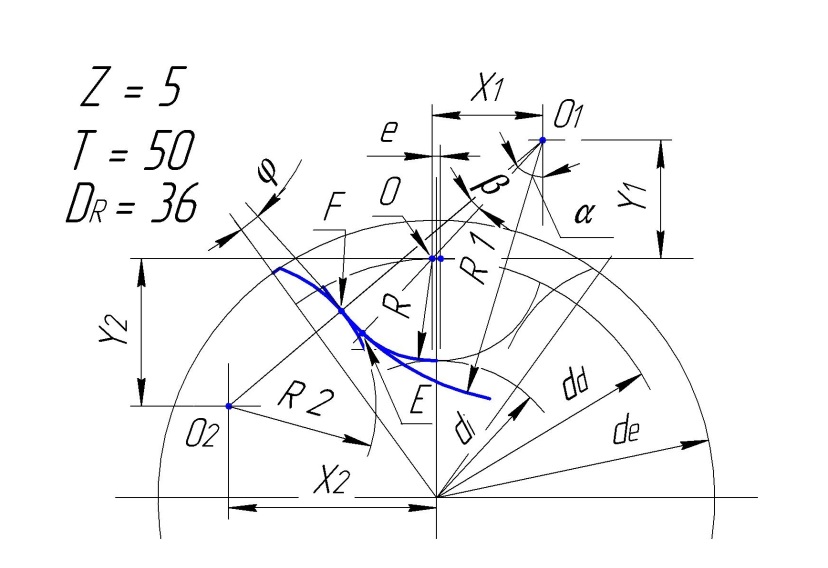
Расчет:

Все в градусах и миллиметрах.

.ddo=t /(sin(180/z))… Делительный диаметр звездочки.

.dn=t*(0,6+(tan(90-(180/z ))))… Наружный диаметр.

.rv=(0,5025*d)+0,05… Радиус впадин

.di=ddo-(rv+rv)… Диаметр дна зубьев.

.r1=(0,8*d)+rv… Радиус сопряжения R1.

.uv=55-(60/z)… Половина угла впадины « а » в градусах.

.us=18-(56/z)… Угол сопряжения « b » в градусах.

.uf=90-((180/z)+uv+us)… Половина угла зуба « f » в градусах.

.e=0,03*t… Смещение центров дуг впадин « е ».

.x1=(0,8*d)*(sin(uv))… Координаты точки О1.

.y1=(0,8*d)*(cos(uv))… Координаты точки О1.

.x2=1,24*d*(cos(180/z))… Координаты точки О2.

.y2=1,24*d*(sin(180/z))… Координаты точки О2.

Радиус головки зуба R2:

.r2=(d*((1,24*(cos( uf )))+(0,8*(cos( us )))-1,3025))-0,05…

…

.ctg( a ) = tan ( 90 – a )… Перевод приведен для справки..

Контрольный расчет:

Задано:

Число зубьев звездочки = 5,0.

Шаг цепи = 50,0.

Диаметр ролика цепи = 36,0.…

Диаметр делительной окружности = 85,065081.

Диаметр окружности выступов = 98,819096.

Диаметр окружности впадин = 48,78508084.

…

Радиус впадин = 18,14.

Радиус сопряжения R1 = 46,94.

Радиус головки зуба R2 = 26,17752.

Половина угла впадины ( угол альфа ) = 43,0.

Угол сопряжения бета = 6,80.

Половина угла зуба ( угол фи ) = 4,20.

Смещение центров дуг впадин E = 1,5.

Координаты точки О 1:

Координата Х 1= 19,64155.

Координата Y 1 = 21,0629866.

Координаты точки О 2:

Координата Х 2 = 36,1145186.

Координата Y 2 = 26,23873.

…….

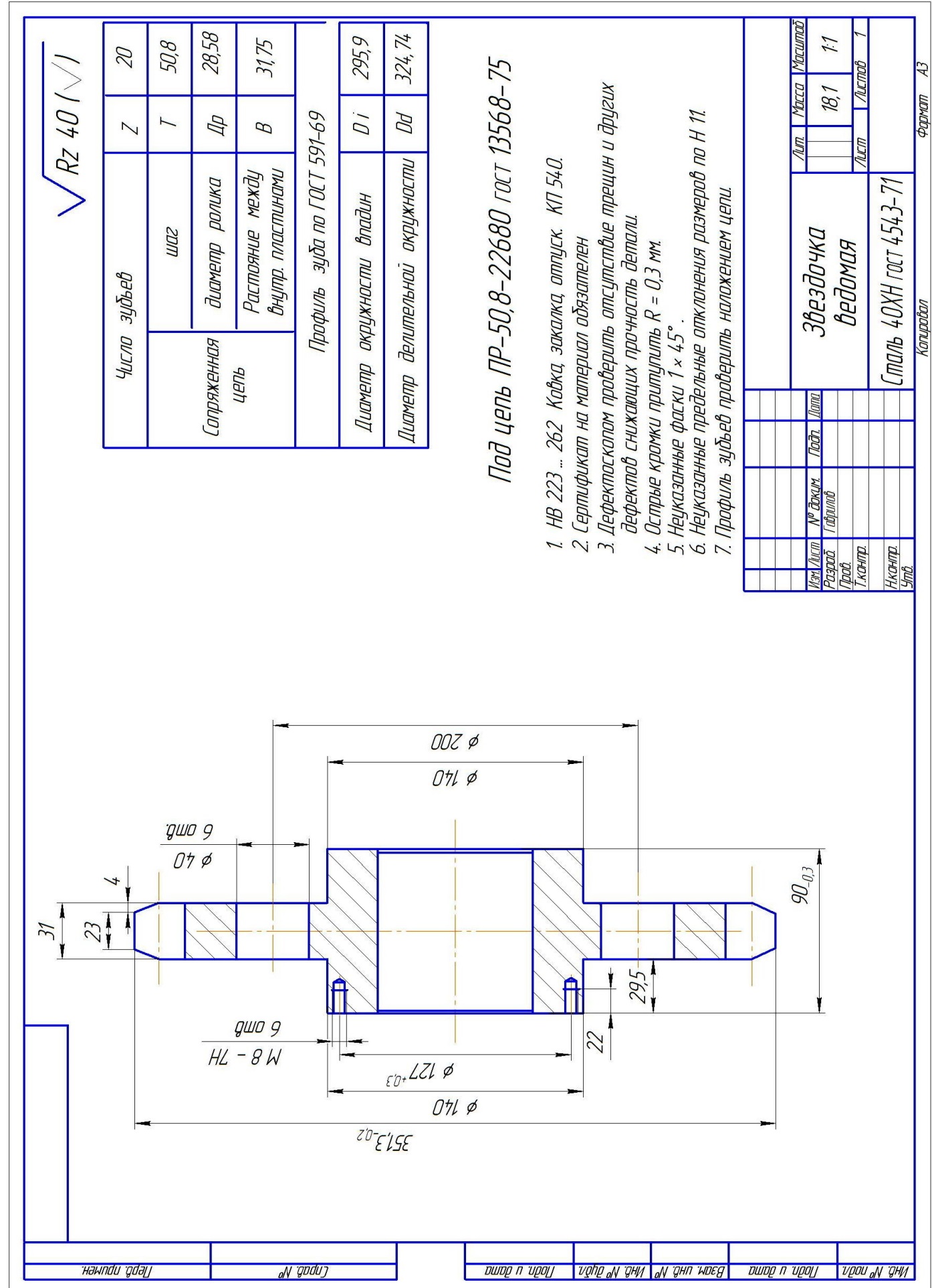
Чертеж приведен для примера. Важно добавить в тех.условиях « Профиль зуба проверить наложением цепи. ».

Прорисовку профиля зуба с размерами профиля на чертеже делают только по требованию цеха – изготовителя. Обычно достаточно указать « профиль звездочки по ГОСТ 591-69. » и ГОСТ и марку цепи.

## « Чертеж звездочки » Ссылка:

Ссылка Studenty.zip : https://disk.yandex.ru/d/orKSVHysYSMK0Q

Studenty.zip : CRC 32 = 77d05e10… Объем -= 77,916,434....

……..

Ссылка Студенту.zip : https://disk.yandex.ru/d/Rbo3M49TP3xMdg

Студенту.zip: CRC 32 = E76A2853… Объем -= 152458350…

…..

В браузере, в адресной строке удалить адрес, который там стоял и вставить скопированный адрес ссылки.

Щелкнуть по ссылке – подтвердить « Посетить ». На странице Яндекс диска нажать « Скачать » « Сохранить ».

Затем – Показать ход загрузки. Браузер пишет « Обычно такие файлы не скачиваем ». Щелкаем правой клавишей мыши – командуем « Разрешить загрузку ». Файл загружается в стандартную папку « Загрузки ».

Для контроля проверить размер файла и CRC32.. Затем распаковать в свою папку.

Расчет CRC32 по программе HashTab_v6.0.0.34 …https://hashtab.ru/…

Расчет пружины сжатия.

Для примера приведен рабочий чертеж пружины сжатия:

Наружный диаметр = 48 мм.

Диаметр проволоки = 6 мм.

Шаг витков = 12 мм.

Свободная длина = 124 мм.

Макс. нагрузка = 100 кгс.

Осадка под макс. нагр. = 56 мм.

…

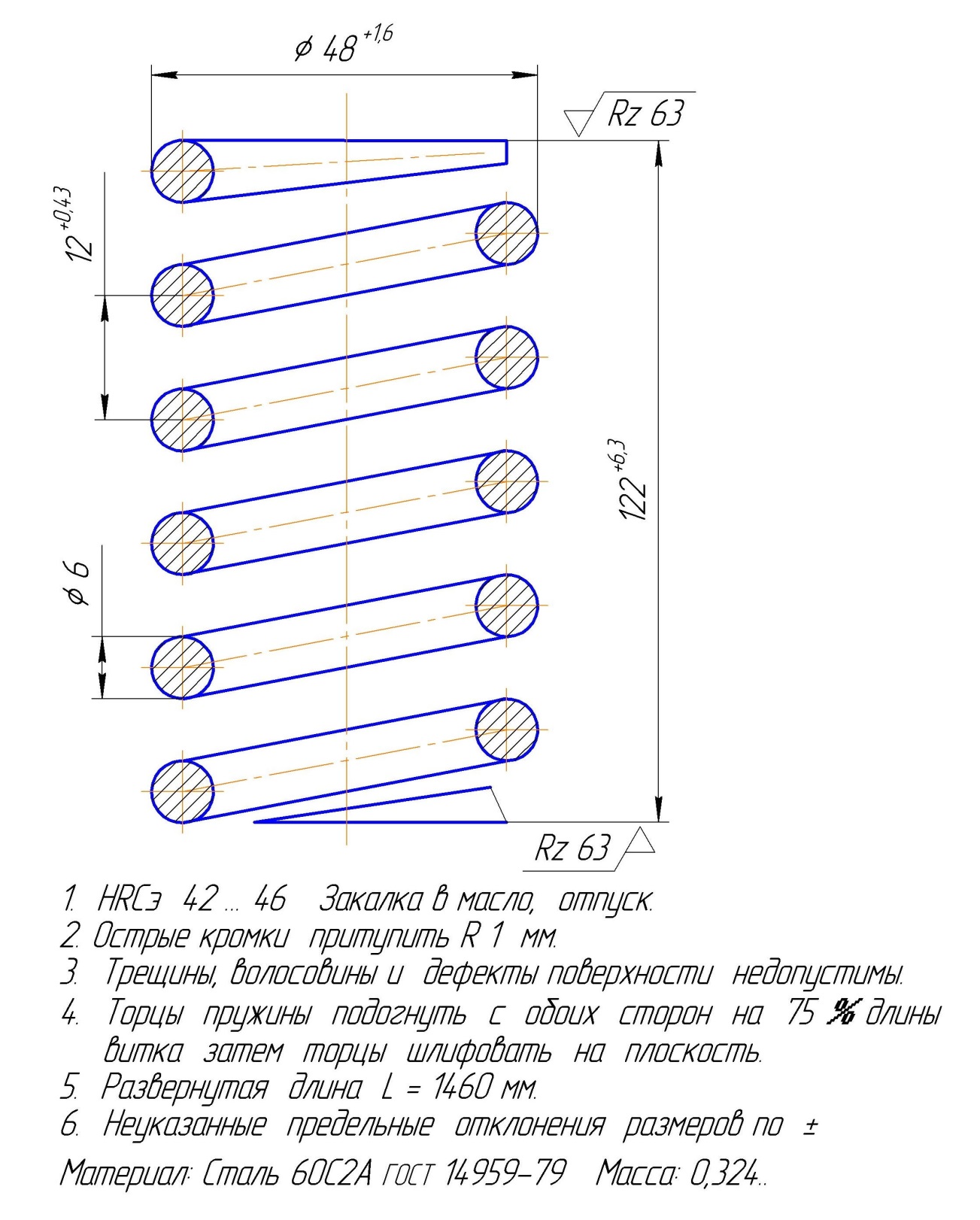
Выполним проверочный расчет пружины сжатия:

Расчет пружины сжатия ( проверочный ).

Пружины сжатия различают по классам:

Первый класс – циклическая нагрузка на Пять миллионов циклов.

( по Анурьеву выпуска 2001 г. – Десять миллионов циклов ).

Выполняют из сталей 60С2А и 65С2ВА ГОСТ 14963-69 HRC 46 … 52.

и из стали 50ХФА ГОСТ 14963-69 HRC 44 … 50.

допускаемое касательное напряжение для этих сталей не более 56 кгс/кв.мм.

Второй класс – циклическая нагрузка на Сто тысяч циклов.

Стали те же самые, HRC без изменений – ( напряжение увеличено ).

Допускаемое касательное для этих сталей в этом классе не более 96 кгс/кв.мм.

Соударения витков для этих классов не допускается.

Третий класс – циклическая нагрузка на Две тысячи циклов.

Стали те же самые, HRC 53 … 57 – ( напряжение увеличено ).

Допускаемое касательное для этих сталей в этом классе не более 135 кгс/кв.мм.

Все размеры в расчете в миллиметрах – материал – сталь : плотность q = 7,95 т/куб.м.

…………

Расчет параметров пружины сжатия

Исходные данные:

Наружный диаметр пружины d = 48..

Диаметр проволоки пружины dp = 6..

Шаг навивки пружины tp = 12..

Полный ход пружины до выборки зазоров между витков ws = 56..

Рабочее усилие на пружину p2 = 100 кгс..

.....

Расчет:

.do=d-dp… Средний диаметр.

.z=dp*dp*dp*dp*1000/(do*do*do)… Жесткость одного витка..

Жесткость одного витка z = 17,4927 кгс/мм.

.c=do/dp…

.k=(((4*c)-1)/((4*c)-4))+(0,615/c)…

Коэф. К = p1=(tp-dp)*z … Gsf = 461030/2725231222…|

Усилие при полном сжатии одного витка p1 = 104,9563 кгс.

.tk=8*k*p1*do/(Pii*dp*dp*dp)…

Касательное напряжение при полном сжатии витка tk = 63,0309 кгс/мм2 .

.tk1=8*k*p2*do/(Pii*dp*dp*dp)…

Касательное напряжение при рабочем усилии tk1= 60,0545 кгс/мм2 .

L1v=p2/z…

Деформация одного витка при рабочем усилии L1v = 5,7167 мм.

.с = sqrt ((Pii*do*Pii*do)+(tp*tp))… Квадрат гипотенузы.

Вариант № 1.

Пружина с подогнутыми витками – но без подшлифовки крайних витков.

.w=(ws/(tp-dp))+3…

Число витков полное c учетом подогнутых витков w = 12,3333…

.ll=((w-3)*tp)+(3*dp)…

Свободная габаритная длина пружины ll = 130,0 мм.

.llr=c*w…

Развернутая длина проволоки пружины llr = 1634,06 мм.

.s=Pii*dp*dp/4…

.px=7,95*s*llr/1000000…

Вес пружины px = 0,367 кг.

.....

Вариант № 2.

Пружина с подогнутыми крайними витками,

крайние витки сошлифованы на плоскость перпендикулярную оси пружины.

.we=(ws/(tp-dp))+2 …

.lle=((w-3)*tp)+(2*dp)…

.llre=c*we …

Число витков полное ( с подогнутыми витками ) we = 11,3333…

Свободная габаритная длина пружины lle = 124,0 мм.

Развернутая длина проволоки пружины llre = 1501,57 мм.

.se=Pii*dp*dp/4…

.pxe=7.95*se*llre/1000000…

Вес пружины pxe = 0,338 кг.

Все размеры в миллиметрах – материал – сталь q = 7,95 т / м3

…..

Примечание:

При мелкосерийном производстве точно определить число рабочих витков,

длину пружины под нагрузкой не получится, так как подгиб концевых витков выполняется

с большими отклонениями по размеру.

Пружину в единичном производстве обычно навивают на цилиндр равный внутреннему диаметру пружины.

Цилиндр зажимают в патрон токарного станка, один конец проволоки прочно прикрепляют к цилиндру.

Другой конец проволоки проходит через поводок закрепленный в резцодержателе станка.

Станок включают на нарезание резьбы с шагом навивки пружины. Скорость шпинделя 20..60 об/мин.

Направление вращения – обратное ( при взгляде от суппорта – по часовой стрелке ) при ходе суппорта от патрона. Количество витков делают больше чертежного минимум на два витка для подгонки.

Навив пружину – не ослабляя усилие на проволоку – надежно закрепляют второй конец проволоки на цилиндре.