The Wonders of Arithmetic from Pierre Simon de Fermat

P2(P–4)–4δ1P–δ12=2 (4)

Now we will certainly notice that δ1>P otherwise, by the same logic as above, on the left (4) we get P2(P–9)>2 what again does not suitable, then there must exist a number δ2=δ1–P and after substituting δ1=P+δ2 in (4), we obtain P2(P–9)–6δ2P–δ22=2 (5)

Here one can no longer doubt that this will continue without end. Indeed, by trying δi=P each time we get P2(P−Ki)>2. Whatever the number of Ki this equation is impossible because if Ki

3 then P2(P−Ki)>2 and if Ki≥P then this option is excluded because then P2(P−Ki)≤0

To continue so infinitely is clearly pointless, therefore our initial assumption of the existence of another solutions P>3, Q>5 is false and this Fermat's theorem is proven.

In the book of Singh, which we often mention, this task is given as an example of the “puzzles” that Fermat was “inventing”. But now it turns out that the universal descent method and a simple technique with trying, make this task one of the very effective examples for learning at school.

Along with this proof, students can easily prove yet another theorem from Fermat’s letter-testament, which could be solved only by such a world-famous scientist as Leonard Euler:

There are only two squares that increased by 4, give cubes, these squares will be 4 and 121.

In other words, the equation p3=q2+4 has only two integer solutions.

3.4.2. The Fermat’s Golden Theorem

We remind that in the Fermat's letter-testament only a special case of this theorem for squares is stated. But also, this simplified version of the task was beyond the power not only of representatives of the highest aristocracy Bachet and Descartes, but even the royal-imperial mathematician Euler.

However, another royal mathematician Lagrange, thanks to the identity found by Euler, still managed to cope with the squares and his proof of only one particular case of FGT is still replicated in almost all textbooks. However, there is no reasonable explanation that the general proof of the FGT for all polygonal numbers obtained by Cauchy in 1815 was simply ignored by the scientific community.

We begin our study with the formulation of the FGT from Fermat's letter to Mersenne in 1636. It is presented there as follows:

Every number is equal

one, two or three triangles,

one, 2, 3 or 4 squares,

one, 2, 3, 4 or 5 pentagons,

one, 2, 3, 4, 5 or 6 hexagons,

one, 2, 3, 4, 5, 6 or 7 heptagons,

and so on to infinity [36].

Since polygonal numbers are clearly not respected by today's science, we will give here all the necessary explanations. The formula for calculating any polygonal number is represented as

mi = i+(k−2)(i−1)i/2

where m is a polygonal number, i is a serial number, k is the quantity of angles.

Thus, m1=1; m2=k; and for all other i the meaning of mi varies widely as shown in the following table:

Table 1. Polygonal numbers

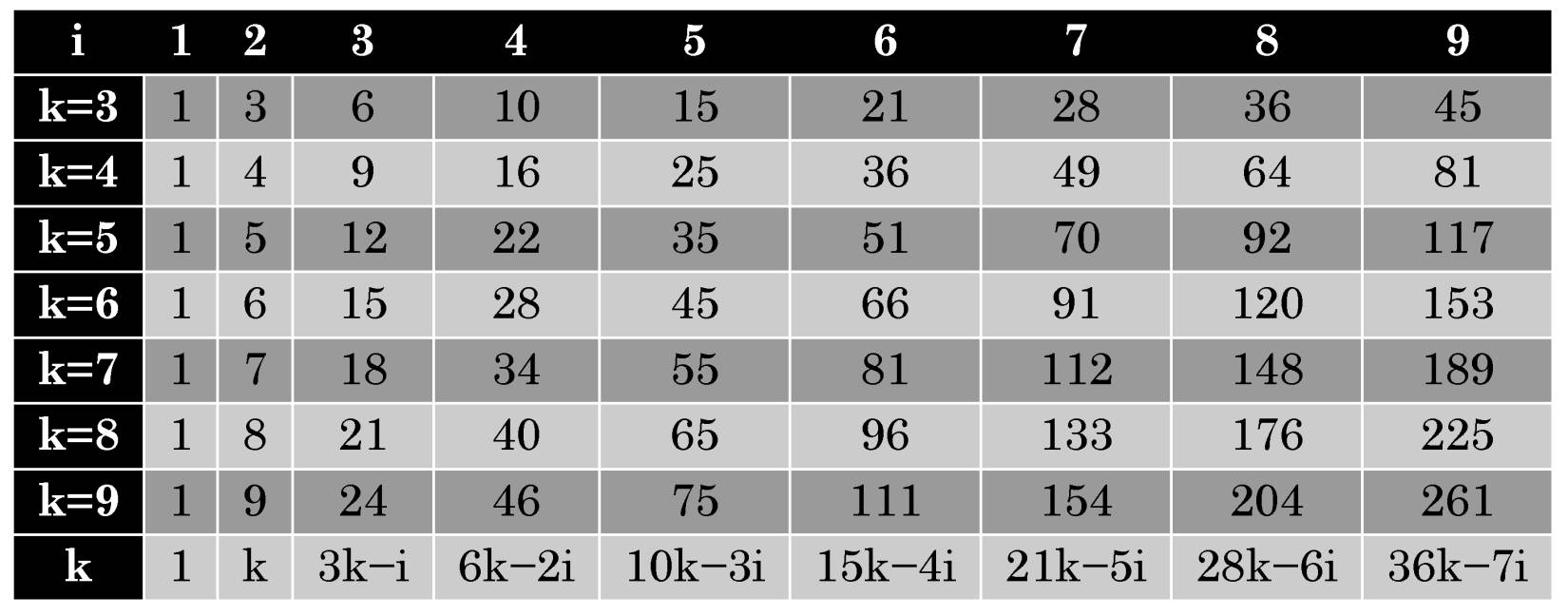
To calculate mi it is enough to obtain only triangular numbers by the formula, which is very easily since the difference between them grows by unit with each step. And all other mi can be calculated by adding the previous triangular number in the columns. For example, in column i=2, numbers increase by one, in column i=3 – by three, in column i=4 – by six etc. i.e. just on the value of the triangular number from the previous column.

To make sure that any natural number is represented by the sum of no more than k k-angle numbers is quite easily. For example, the triangular number 10 consists of one summand. Further 11=10+1, 12=6+6, 13=10+3 of two, 14=10+3+1 of three, 15 again of one summand. And so, it will happen regularly with all natural numbers. Surprisingly that the number of necessary summands is limited precisely by the number k. So, what is this miraculous power that invariably gives such a result?

As an example, we take a natural number 41. If as the summand triangular number will be closest to it 36, then it will not in any way to fit into three polygonal numbers since it consists minimum of 4 ones i.e. 41=36+3+1+1. However, if instead of 36 we take other triangular numbers for example, 41=28+10+3, or 41=21+10+10 then again in some unknown miraculous way everything will so as it stated in the FGT.

At first glance it seems simply unbelievable that it can somehow be explained? But we still pay attention to the existence of specific natural numbers, which are consisting at least of k k-angle numbers and denoted by us as S-numbers. Such numbers are easily to find for example, for triangles – 5, 8, 14, for squares – 7, 15, 23, for pentagons – 9, 16, 31 etc. And this our simple observation allows us directly to move to aim i.e. without using ingenious tricks or powerful "sharpness of mind".

Now to prove the FGT, suppose the opposite i.e. that there exists a certain minimal positive integer N consisting minimum of k + 1 k-angle numbers. Then it’s clear that this our supposed number should be between some k-angle numbers mi and mi+1 and can be represented as

N=mi+δ1 where δ1=N−mi (1)

It is quite obvious that δ1 must be an S-number since otherwise this would contradict our assumption about the number N. Then we proceed the same way as in our example with the number 41 i.e. represent the supposed number as

N = mi-1+δ2 where δ2=N−mi-1

Now δ2 should also be an S-number. And here so we will go down to the very end i.e. before

δi-1=N−m2 =N−k and δi=N−m1=N–1 (2)

Thus, in a sequence of numbers from δ1 to δi, all of them must be S-numbers i.e. each of them will consist of a sum minimum of k k-angle numbers, while our supposed number N will consist minimum of k+1 k-angle numbers. From (1) and (2) it follows:

N− mi =Si (3)

Thus, if we subtract any smaller polygonal number mi from our supposed number N then according to our assumption, the result should be only an S-number. Of course, this condition looks simply unbelievable and it seems that we are already at target, but then how can one prove that this is impossible? …

If we gave an answer to this question here, then this famous Fermat's theorem would immediately turn into the most common school problem and interest to it would be lost. To prevent this from happening, we will stay on the fact that the proof is presented here only by 99% and the remaining 1% will be offered to those who will be interested in order to appreciate the true magnificence of this scientific achievement of Fermat, especially in comparison with the Cauchy’s GFT proof.42

Pic. 34. Title Page the Cauchy's Proof

of the Fermat's Golden Theorem

Pic. 35. One of 43 Pages the Cauchy's Proof

of the Fermat's Golden Theorem

3.4.3. Archimedes-Fermat Problem

The problem statement is as follows:

Let any non-square number be given, you need to find an infinite number of squares, which after multiplication by this number and increasing by unit, will make a square.

Fermat proposed finding solutions for the numbers 61, 109, 149, and 433 [36].

The English mathematician John Wallis managed to find a way to calculate the required numbers using the Euclidean method of decomposing an irrational number into an infinite common fraction. He published his decision under the name "Commercium epistolicum" see pic. 37-38.

Pic. 36. John Wallis

Pic. 37. Title Page of Wallis's Publication Commercium Epistolicum

Although Wallis did not give a complete proof the validity of this method, Fermat nevertheless admitted that he had coped with the task. Euler came very close to the solution when he showed that this fraction is cyclical, but he was not able to complete the proof and this task was finally solved by Lagrange. Later, this Fermat's task also was solved by Gauss in his own way, but for this purpose the extensive theory he created called “Arithmetic of deductions” was involved. And everything would be fine if the Lagrange's proof was not in the category of highest difficulty and the Gauss decision was not based on the most complicated theory. Fermat himself clearly could not follow such ways. About how he himself solved this problem, he reports in the letter-testament to Carcavy in August 1659 [36]: “I recognize that Mr. Frenicle gave various special solutions to this question as well as Mr. Wallis, but a common solution will be found using the method of descent applied skillfully and appropriately." However, this Fermat's solutions so remained as the secret behind seven seals!

Pic. 38. Page 64 Commercium Epistolicum

Demonstrating Wallis Method

We will try here slightly to open the veil over this mystery. To do this, we will look at a simple example of Wallis calculations and then compare it with how one could do these calculations using Fermat's method. So, we need to find the smallest numbers x and y that satisfy the equation Ax2 + 1 = y2. Let A = 29 then calculations by the Wallis method look as follows [32]:

From this sequence of calculations, a chain of suitable fractions is obtained by backward i.e. from a5 to a0 and looks like: 5/1; 11/2; 16/3; 27/5. As a result, we get 70/13. Then the minimum solution would be:

x1√29+у1=(13√29+70)2=1820√29+9801; x1=1820; y1=9820

Wallis was unable to prove that this method of computation gives solutions for any non-square number A. However, he guessed that the chain of computations ends where a6 will be computed by the same formula as a1. To understand the meaning of this chain of calculations, you need to study a very voluminous and extremely difficult theory [7, 14, 19, 23, 26, 32], which Fermat could not have developed at that time. Since no Fermat's manuscripts on arithmetic have survived, a natural question arises: how could he formulate such a difficult problem, about which there was very little information before him?

For today's science such a question is clearly beyond its capabilities since for it the pinnacle of achievements in solving Fermat's problems is any result even inflated to such incredible dimensions that we have today. However, it is difficult to imagine how much this our respected science will be dejected when from this book it learns that the problem was solved by Fermat not for great scientists, but … for schoolchildren!!! However, here we cannot afford to grieve science so much, so we only note that the example given in the textbooks is very unfortunate since it can be solved quite simply, namely: x = 2mz, where m

Obviously, in textbooks it would be much more appropriate to demonstrate an example with the number 61 i.e. the smallest number proposed by Fermat himself. How he himself solved this problem is unknown to science, but we have already repeatedly demonstrated that it is not a problem for us to find out. We just need to look once more into the cache of the Toulousean senator and as soon as we succeeded, we quickly found the right example so that it could be compared with the Wallis method. In this example you can calculate x = 2mz, where m and z are solutions to the corresponding equation 61m2 – z2 = 1. Then the chain of calculations is obtained as follows:

61m2−z2=1

m=(8m1±z1)/3=(8×722+5639)/3=3805; z2=61×38052−1=297182

61m12−z12=3

m=(8m1±z1)/3=(8×722+5639)/3=3805; z12=61×7222−1=297182

61m22−z22=9

m=(8m1±z1)/3=(8×722+5639)/3=3805; z22=61×1372−1=297182

61m32−z32=27

m3=(8m4±z4)/3=(8×5+38)/3=26; z32=61×262−27=2032

61m42−z42=81

m4=(8m5±z5)/3=(8×2−1)/3=5; z42=61×52−81=382

61m52−z52=243

m5=2; z52=1

We will not reveal all nuances of this method, otherwise all interest to this problem would have been lost. We only note that in comparison with Wallis method where the descent method is not used, here it is present in an explicit form. This is expressed in the fact that if the numbers m and z satisfying the equation 61m2–z2=1 exist, then there must still exist numbers m1

m=3805; z=29718

x=2mz=2×3805×29718=226153980

y=√(61×2261539802+1)=1766319049

Of course, connoisseurs of the current theory will quickly notice in this example that the results of calculations obtained in it will exactly coincide with those that can be obtained by the Wallis' method. However, for this they will have to use the irrational number √61, and our example with Fermat's method showed that it is possible to do calculations exclusively in the framework of arithmetic i.e. only in natural numbers. There is no doubt also that experts without much effort will guess how to get the formulas shown in our example. However, it will not be easily for them to explain how to apply this Fermat's method in the general case because from our example it is not at all clear how it is possible to determine that the ultimate goal is to solve the equation 61m52 – z52 = 243 from which calculations should be performed with a countdown.

It would be simply excellent if today's science could explain Fermat's method in every detail, but even the ghostly hopes for this are not yet visible. It would be more realistic to expect that attempts will be made to refute this example as demonstration a method of solving the problem unknown to science. Nevertheless, science will have to reckon with the fact that this example is still the only one in history (!!!) confirmation of what Fermat said in his letter-testament. When this secret is fully revealed, then all skeptics will be put to shame and they will have no choice, but to recognize Fermat as greater than all the other greatest scientists because they were recognized as such mainly because they created theories so difficult for normal people to understand that they could only cause immense horror among students who now have to take the rap for such a science.43

https://www.youtube.com/watch?v=wFz8W2HsjfQ

https://www.youtube.com/watch?v=cUytn2SZ1n4

https://www.youtube.com/watch?v=ZhVNOgaBStY

In this sense, the following example of solving a problem using the descent method will be particularly interesting because it was proposed in a letter from Fermat to Mersenne at the end of 1636, i.e. the age of this task is almost four centuries! Euler's proof [8] was incorrect due to the use of "complex numbers" in it. However, even the revised version of André Weil in 1983 [17] is too complex for schooling.

3.4.4. Fermat’s Problem with Age 385 years

In the original version in 1636 this task was formulated as follows:

Find two square-squares, which sum is equal to a square-square,

or two cubes, which sum is a cube.

This formulation was used by Fermat's opponents as the fact that Fermat had no proof of the FLT and limited himself to only these two special cases. However, the very name "The Fermat’s Last Theorem" appeared only after the publication of "Arithmetic" by Diophantus with Fermat's remarks in 1670 i.e. five years after his death. So, there is no any reason to assert that Fermat announced the FLT in 1637.

The first case for the fourth power we have presented in detail in Appendix II. As for the case for the third power, Fermat's own proof method restored by us below, will not leave any chances to the solutions of this problem of Euler and Weil to remain in history of science, since from the point of view of the simplicity and elegance of the author's solution this problem, they will become just unnecessary.

Now then, to prove that there are no two cubes whose sum is a cube, we use the simplest approach based on divisibility of numbers, what means that in the original equation

a3+b3 = c3 (1)

the numbers a, b, and c can be considered as coprime ones, i.e. they do not have common factors, but in general case this is not necessary, since if we prove that equation (1) cannot have solutions in any integers, including those with common factors, then we will prove that coprime numbers also cannot be solutions of the original equation. Then we assume that both sides of equation (1) in all cases must be divisible by the number c2, then equation (1) can be represented as

c3 = c2(x+y) = a3+b3 (2)

In this case, it is easily to see that there is only one way to get solutions to equation (1) when the numbers c, x, y, and x+y are cubes, i.e.

с = x+y = p3+q3= z3; x = p3; y = q3 (3)

Then equation (1) must have the form:

(z3)3 = (z2)3(p3+q3) (4)

Thus, we found that if there are numbers a, b, and c that satisfy equation (1), then there must be numbers p

p3+q3= z3

If we now apply the same approach to solving this equation, that we applied to solving equation (1), we will get the same equation, only with smaller numbers. However, since it is impossible to infinitely reduce natural numbers, it follows that equation (1) has no solutions in integers.

At first glance, we have received a very simple and quite convincing proof of the Fermat problem by the descent method, which no one has been able to obtain in such a simple way for 385 years, and we can only be happy about it. However, such a conclusion would be too hasty, since this proof is actually incorrect and can be refuted in the most unexpected way.

However, this refutation is so surprising that we will not disclose it here, because it opens the way not only for the simplest proof of the FLT, but also automatically allows to reduce it to a very simple proof of the Beal conjecture. The disclosure the method of refuting this proof would cause a real commotion in the scientific world, therefore we will include this mystery among our riddles (see Appendix V Pt. 41).

So, we have demonstrated here solving to Fermat's problems (only by descent method!):

1) The proof of the Basic theorem of arithmetic.

2) The proof of the Fermat's theorem on the unique solving the

equation p3 = q2 + 2.

3) A way to prove Fermat's Golden Theorem.

4) A Fermat's way to solve the Archimedes-Fermat equation

Ax2 + 1 = y2.

5) The proof method of impossibility a3+b3=c3 in integers, which

opens a way to simplest proofs of the FLT and Beal conjecture.

6) A Fermat's proof his grandiose discovery about primes in the

form 4n + 1 = a2 + b2 which we have presented in another style in

Appendix IV, story Year 1680.

Over the past 350 (!!!) years after the publication of these problems by Fermat, whole existing science could not even dream of such a result!

3.5. Parity Method

Before we embarking on the topic "Fermat's Last Theorem" we note that this problem was not solved by Fermat himself using the descent method, otherwise in his FLT formulation there would be no mention of a "truly amazing proof", which certainly related to other methods. Therefore, to the above examples of the application of the descent method we will add our presentation of two methods unknown to today's science. The most curious of these is the parity method.

3.5.1. Defining Parity as a Number

The Basic theorem of arithmetic implies a simple, but very effective idea of defining parity as a number, which is formulated as follows:

The parity of a given number is the quantity of divisions this number by two without a remainder until the result of the division becomes odd.

Let's introduce the parity symbol with angle brackets. Then the expression ‹x› = y will mean:

the parity of the number x is equal to y. For example, the expression "the parity of the number forty is equal to three" can be represented as: ‹40›= 3. From this definition of parity, it follows:

– parity of an odd number is zero.

– parity of zero is infinitely large.

– any natural number n can be represented as n = 2w (2N – 1)

where N is the base of a natural number, w is its parity.

3.5.2. Parity Law

Based on the above definition the parity, it can be stated that equal numbers have equal parity. In relation to any equation this provision refers to its sides and is absolutely necessary in order for it to have solutions in integers. From here follows the parity law for equations:

Any equation can have solutions in integers if and only if the parities of both its sides are equal.

The mathematical expression for the parity law is WL = WR where WL and WR are the parities of the left and right sides of the equation respectively. A distinctive feature of the parity law is that the equality of numbers cannot be judged by the equality of their parity, but if their parities are not equal, then this certainly means the inequality of numbers.

3.5.3. Parity Calculation Rules

Parity of a sum or difference two numbers a and b

If ‹a› < ‹b› then ‹a ± b› = ‹a›.

It follows in particular that the sum or difference of an even and an odd number always gives a number with parity zero. If ‹a› = ‹b› = x then either ‹a + b› = x + 1 wherein ‹a – b› > x + 1

or ‹a – b› = x + 1 wherein ‹a + b› > x + 1

These formulas are due to the fact that

‹(a + b) + (a – b)› = ‹2a› = ‹a› + 1

It follows that the sum or difference of two even or two odd numbers gives an even number.

Parity of a sum or difference two power number an and bn

If ‹a› < ‹b› then ‹an ± bn› = ‹an›. If ‹a› = ‹b› = x then

only for even n:

‹an – bn› = ‹a – b›+ ‹a + b›+ x(n – 2) + ‹n› – 1

‹an + bn› = xn + 1

only for odd n:

‹an ± bn› = ‹a ± b› + x(n – 1)

When natural numbers multiplying, their parities are added up

‹ab› = ‹a› + ‹b›

When natural numbers dividing, their parities are subtracted

‹a : b› = ‹a› – ‹b›

When raising number to the power, its parity is multiplied

‹ab› = ‹a› × b

When extracting the root in number, its parity is divided

‹ b√a› = ‹a› : b

3.6. Key Formula Method

To solve equations with many unknowns in integers, an approach is often used when one more equation is added to the original equation and the solution to the original is sought in a system of two equations. We call this second equation the key formula. Until now due to its simplicity, this method did not stand out from other methods, however we will show here how effective it is and clearly deserves special attention. First of all, we note an important feature of the method, which is that:

Key formula cannot be other as derived from the original equation.

If this feature of the method is not taken into account i.e. add to the original equation some other one, then in this case, instead of solving the original equation we will get only a result indicating the compatibility of these two equations. In particular, we can obtain not all solutions of the original equation, but only those that are limited by the second equation.

In the case when the second equation is derived from the initial one, the result will be exhaustive i.e. either all solutions or insolvability in integers of the original equation. For example, we take equation z3 = x2 + y2. To find all its solutions we proceed from the assumption that a prerequisite (key formula) should be z = a2 + b2 since the right-hand side of the original equation cannot be obtained otherwise than the product of numbers which are the sum of two squares. This is based on the fact that: