
Полная версия
Веселые задачи. Две сотни головоломок

Яков Исидорович Перельман
Веселые задачи
Предисловие автора

Цель этой книжечки – дать материал для приятной умственной гимнастики, для тренировки сообразительности и находчивости. Предназначенная пополнить досуг юных математиков, книжка содержит, однако, не только математические головоломки: наряду с задачами арифметическими и геометрическими, в сборнике представлены головоломки из области физики, мироведения и логики. Есть здесь и задачи, не примыкающие ни к какому учебному предмету, но все же полезные как упражнения, подготавливающие ум к более серьезной работе. Так, задачи на перестановки и размещения приучают к систематическим поискам решения, зрительные обманы способствуют развитию наблюдательности, развлечения с разрезыванием фигур и составлением силуэтов развивают геометрическое воображение.
На русском языке уже имеются сборники подобного типа. Появление еще одного было бы излишним, если бы составитель не стремился освежить традиционный материал несколькими десятками частью новых, придуманных им самим, частью малоизвестных задач, почерпнутых из иностранных источников. Задачи предполагают у читателя лишь элементарные познания и предназначены преимущественно тем, кому еще предстоит изучать математику.
Второе издание этой книги, вышедшее в 1919–1920 гг. в весьма большом числе экземпляров, было перепечатано с первого без существенных изменений.
Для третьего издания текст заново отредактирован и некоторые задачи по различным соображениям заменены другими.
Октябрь, 1924
Первая сотня головоломок
Головоломные размещения и занимательные перестановки
1. Белки и кролики
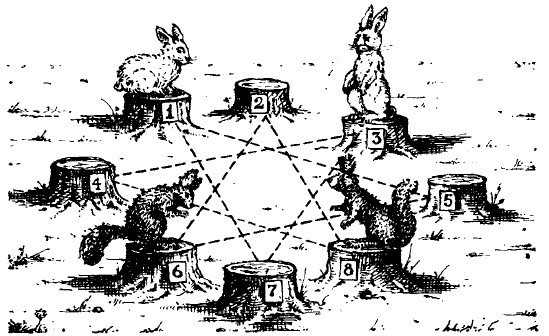
Перед вами восемь перенумерованных пней (рис. 1). На пнях 1 и 3 сидят кролики, на пнях 6 и 8 – белки. И белки, и кролики почему-то недовольны своими местами и хотят обменяться пнями: белки желают сидеть на местах кроликов, а кролики – на местах белок. Попасть на новое место они могут, прыгая с пня на пень по следующим правилам:
1) прыгать с пня на пень можно только по тем линиям, которые показаны на рисунке; каждый зверек может делать несколько прыжков кряду;
2) два зверька на одном пне поместиться не могут, поэтому прыгать можно только на свободный пень. Имейте также в виду, что зверьки желают обменяться местами за наименьшее число прыжков. Впрочем, меньше чем 16 прыжками им не обойтись.
Как же они это сделают?

Рис. 1. На полянке.
2. Чайный сервиз
Мне пришлось как-то целый вечер ждать поезд на маленькой станции. Не было ни книг, ни газет, ни собеседников, и я не знал, чем наполнить часы ожидания. К счастью, я вспомнил об одной занимательной задаче, которая незадолго до того попалась мне в иностранном журнале. Задача состояла в следующем.
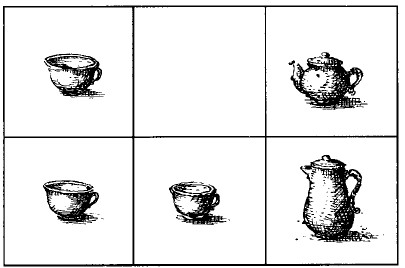
Рис.2.Стол, накрытый к чаю.
Стол разграфлен на 6 квадратов, в каждом из которых, кроме одного, помещается какой-нибудь предмет. Я воспользовался чайной посудой и разместил по квадратам чашки, чайник и молочник, как показано на рис. 2.
Суть задачи в том, чтобы поменять местами чайник и молочник, передвигая предметы из одного квадрата в другой по определенным правилам, а именно:
1) предмет перемещать только в тот квадрат, который окажется свободным;
2) нельзя передвигать предметы по диагонали квадрата;
3) нельзя переносить один предмет поверх другого;
4) нельзя также помещать в квадрат более одного предмета, даже временно.
Эта задача имеет много решений, но интересно найти самое короткое, т. е. обменять местами чайник и молочник за наименьшее число ходов.
В поисках решения незаметно прошел вечер; я покидал станцию, так и не найдя кратчайшего решения.
Может быть, читатели найдут его? На всякий случай предупреждаю, что искомое наименьшее число ходов все же больше дюжины, хотя и меньше полутора дюжин.
3. Автомобильный гараж
На нашем чертеже изображен план автомобильного гаража с помещениями для двенадцати автомобилей. Но помещение так неудобно, так мало, что у заведующего гаражом постоянно возникают затруднения. Вот одно из них. Предположим, что восемь автомобилей стоят так, как показано на рис. 3. Автомобили 1,2, 3 и 4 необходимо поменять местами с автомобилями 5, 6, 7 и 8.
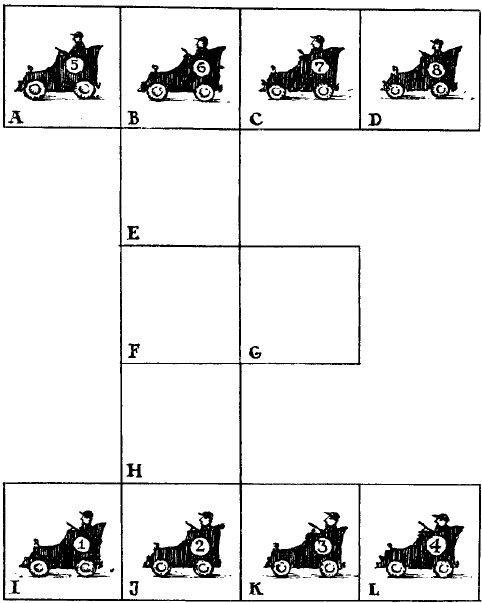
Рис. 3. В гараже.
Как это сделать за наименьшее число переездов?
Надо заметить, что два автомобиля двигаться одновременно не могут и что в каждом отсеке гаража помещается только один автомобиль.
4. Три дороги
Три брата – Петр, Павел и Яков – получили невдалеке от их домов три участка земли, расположенные рядом. Каждый устроил на своем участке огород. Как видно из рис. 4, дома Петра, Павла и Якова и отведенные братьям земельные участки расположены не совсем удобно. Но братья не могли договориться об обмене. А так как кратчайшие пути к огородам пересекались, то между ними вскоре начались столкновения, перешедшие в ссоры. Желая прекратить распри, братья решили отыскать такие пути к своим участкам, чтобы не пересекать друг другу дороги. После долгих поисков они нашли такие три пути и теперь ежедневно ходят на свои огороды, не встречаясь друг с другом.
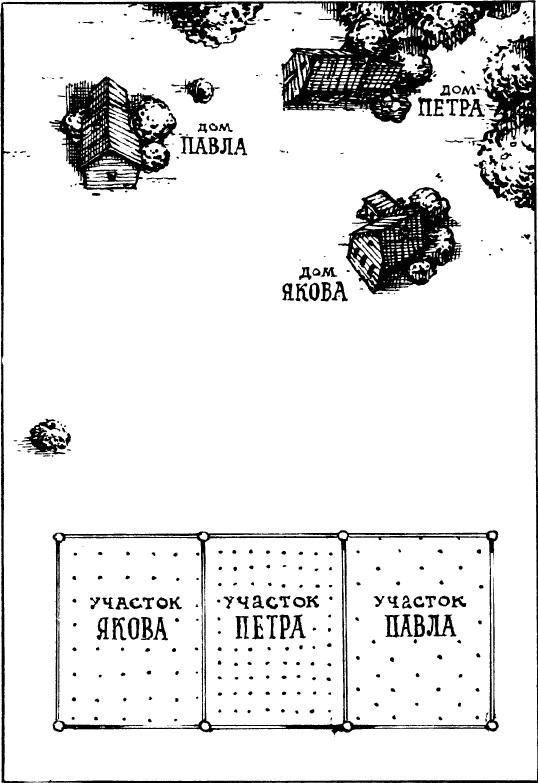
Рис. 4. Три дома – три участка.
Можете ли вы указать эти пути?
5. Муха на занавеске
На оконной занавеске с рисунком в клетку уселись 9 мух. Случайно они расположились так, что никакие две мухи не оказались в одном и том же ряду – ни прямом, ни косом (рис. 5).
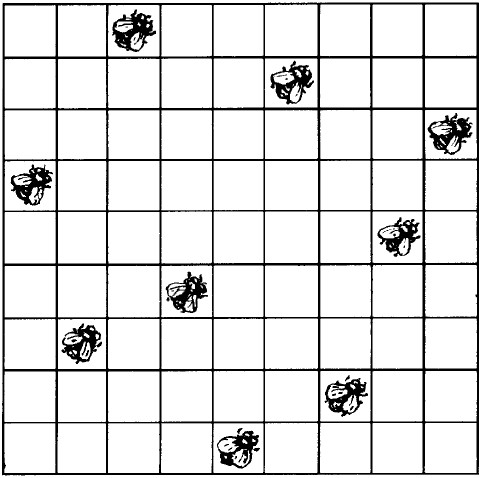
Рис. 5. Мухи на занавеске.
Спустя несколько минут три мухи сменили места и переползли в соседние, незанятые клетки; остальные 6 не двигались. Но забавно: хотя три мухи перешли на другие места, все 9 снова оказались размещенными так, что никакая пара не находилась в одном прямом или косом ряду. Можете ли вы сказать, какие три мухи и куда пересели?
Конец ознакомительного фрагмента.
Текст предоставлен ООО «Литрес».
Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.









