
Полная версия
Рассуждения об основах физики
Теперь нам становится понятным, почему ситуация с линейками, о которых велись рассуждения выше, становится неразрешимой. Верность или неверность способов измерения потеряла смысл, потому что ещё до этого (т. е. при выводе преобразований Лоренца) потеряло смысл понятие измерения.
А как обстоят дела с измерениями в классической механике? Здесь используются преобразования Галилея, а они, как легко видеть, не отменяют Аксиомы. В самом деле, преобразования Галилея преобразуют сферу (2. 3) в такую:
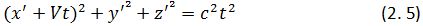
Сфера (2. 5) совпадает со сферой (2. 3). Радиус сферы (2. 5) равен радиусу сферы (2. 3) потому, что в преобразованиях Галилея t = tI. Наличие слагаемого Vt в скобках первого члена говорит о том, что центр сферы (а вместе с ним и источник света) двигаются по отношению к наблюдателю со скоростью (– V) или (что, то же самое), наблюдатель двигается по отношению к центру сферы со скоростью V. И все это, ни коим образом, не противоречит реальной физической ситуации. Преобразования Галилея не отменяют Аксиомы; напротив, они ей строго подчиняются. Поэтому в классической механике измерения возможны и имеют ясный физический смысл.
2. 5. Релятивистская сфера
Но есть еще опыт (наипростейший, очищенный от всего лишнего, что могло бы помешать правильно рассуждать). И мы не можем не упомянуть о нем. Пусть точечный источник света испускает сферический волновой фронт. Каков будет радиус сферы по истечению времени T? Ответ: радиус будет равен cT. А каков будет её диаметр? Ответ (релятивистский): согласно постулату о постоянстве скорости света диаметрально противоположные точки этой сферы удаляются друг от друга также со скоростью света c, поэтому диаметр сферы также равен cT. Диаметр сферы оказался равен её радиусу! Легко видеть, что при других скоростях расширения сферы (меньших c), «релятивистская» сфера всегда будет обладать следующим, неприятным, свойством: диаметр «релятивистской» сферы всегда меньше её удвоенного радиуса (это следует из релятивистской формулы сложения скоростей [2, с. 371]). Такую сферу не сможет построить ни один геометр. А не построивши её, геометр ничего и не сможет измерить. А вслед за ним ничего не сможет измерить и физик. И это потому, что в теории относительности нет Аксиомы. На наш взгляд, достаточно рассмотреть только этот один опыт, чтобы понять всю бессмысленность каких-либо измерений в теории относительности.
2. 6. Подмена одного понятия другим
Подмена одного понятия на другое (не равносильное прежнему), довольно распространенная ошибка в логических рассуждениях. Она имеется и в теории относительности. Это – незаконная подмена тензора одного ранга на тензор другого ранга. В теории относительности вектор скорости света

заменяется скаляром c, то есть имеет место подмена: c вместо c. В самом деле. В теории относительности не существует понятия – проекции вектора скорости света на оси координат, то есть чисел – c1,c2,c3. Это означает нарушение правил тензорной алгебры. Аналогично при введении четырехмерного пространства-времени скаляр ct заменяется на вектор, то есть:

Здесь слева – вектор, а справа – скаляр потому, что ie4 есть единичный вектор пространства L4 с базисом (e1, e2, e3, ie4) и этот базис вводится совершенно независимо от каких-либо существующих скалярных величин (в том числе и скалярной величины – времени). Трехмерное пространство L3 (e1, e2, e3) является подпространством указанного выше четырехмерного пространства L4 и то, что верно в L3 верно так же и в L4. Но в L3 проекций скалярной величины времени на оси координат не существует, а значит, таких проекций не будет существовать и в L4. Скалярная величина – время в подпространстве L3 остается таковой (скалярной) и в пространстве L4. Нетрудно видеть, что эти подмены есть также следствия отсутствия Аксиомы. В самом деле; если при выводе преобразований Лоренца мы запросто заменяем одну сферу на другую, то почему тогда нам нельзя заменить один геометрический объект на другой? (Скаляр и вектор это – разные геометрические объекты). Таким образом, введение четырехмерного пространства-времени по схеме (2. 6) не является обобщением. Это – ошибка. Эта математическая ошибка тотчас становится и физической потому, что физические величины описываются тензорами.
Примечание. Ошибочность схемы (2. 6) можно установить и в более простых рассуждениях. Мы имеем формулу: F = am; но мы не можем сказать, сколько килограммов соответствуют 1 Н потому, что существуют различные ускорения. Мы имеем формулу: U = RI; но мы не можем сказать, сколько ампер соответствуют 1 В потому, что существуют различные сопротивления. Мы имеем формулу: s = Vt; но мы не можем сказать, сколько секунд соответствуют 1 м потому, что существуют различные скорости. Но сторонники теории относительности знают, сколько секунд соответствуют 1 метру потому, что в схеме (2. 6) они всегда умножают время t на одно и то же число c – скорость света. Они думают, что в мире существует только одна эта скорость (скорость света) и никаких других. Как они это узнали? Абсурдность ситуации очевидна.
Подчеркнем ещё раз; давно пора развеять миф о том, что введение четырехмерного пространства-времени есть обобщение, а не ошибка.
2. 7. Теория относительности и субъективный идеализм
Ирландский философ Беркли (1685 – 1753 г.) утверждал, что материальные объекты существуют, только будучи воспринимаемыми. В наше время сторонники теории относительности утверждают, что сфера, за которой не наблюдают, отличается от сферы, за которой ведется наблюдение. Последнее утверждение принципиально ничем не отличается от утверждений Беркли; оно является толкованием, основанном на субъективном идеализме. Может ли физик изучать законы природы, оставаясь на позициях субъективного идеализма? Конечно, может, но от этого нет никакой пользы (но много вреда). В самом деле: физику, конечно, важно то, чего он наблюдает, но ему гораздо важнее знать то, что будет происходить, когда он не имеет возможности наблюдать. Это – материалистическая позиция. Этой же позиции придерживаются и другие науки, например, химия. Субъективный идеализм уводит нас в мир иллюзий, которые не имеют никакого отношения к нашему, реальному миру (например, «парадокс близнецов» – типичная иллюзия теории относительности).
2. 8. Математический аппарат и теория относительности
Мы уже упоминали о том, что математика, в которой используются знаки: больше, меньше, равно, плюс, минус, умножить и т. д.; покоится на Аксиоме. Но в теории относительности этой Аксиомы нет. В таком случае правомерно ли использование традиционной математики в теории относительности? Конечно, нет. Если в теории нет Аксиомы, то и в математике, которая описывает эту теорию, мы также должны избавиться от Аксиомы. Но это будет уже другая математика. Здесь мы наблюдаем очередную непоследовательность в действиях сторонников теории относительности, каковых у них немало.
2. 9. Выводы
Итак, чтобы разобраться в измерениях в теории относительности, не обязательно изучать линейку на атомном уровне. Достаточно сравнить действия математика и физика в измерениях и выяснить, где физики наделали ошибок. Перечислим их (некоторые, но не все).
Физики в теории относительности отменили Аксиому и лишились возможности что-либо измерить. А почему отменили? А потому, что вывели преобразования Лоренца (а из них запрещенные подмены, см. преобразование (2. 6)). А зачем им это понадобилось? А затем, что того требует постулат о постоянстве скорости света. А как они о нём узнали? А от Эйнштейна. А как узнал о нем Эйнштейн? Точно мы не знаем. У Эйнштейна были некоторые основания для введения этого постулата, но эти основания были далеко не достаточны. А в таком случае, не приходило ли вам в голову, господа физики, что такого постулата и нет вовсе? Приходило, но это считается ересью. А то, что диаметр «релятивистской» сферы всегда меньше её удвоенного радиуса, это – не ересь? Вот мы и добрались до той первой ошибки, за которой последовали перечисленные выше: постулат о постоянстве скорости света был принят без достаточных на то оснований. Роковую роль здесь имело то обстоятельство, что физики неправильно использовали часы при измерении времени. При измерении времени, они не учитывали слагаемое переноса часов (оно неизбежно возникает, если часы при измерениях перемещаются). Для одномерного прямолинейного (по оси OX) движения часов это выглядит так: tχ = t + x/c, здесь tχ – показания часов; t – истинное время; x – сдвиг часов по оси OX при измерениях (Гл. 1, формула(1. 10)) . Для трехмерного движения – см. (Гл.1, формула (1. 20)).
При учете этого обстоятельства, постулат о постоянстве скорости света отменяется, и мы возвращаемся к преобразованиям Галилея (формулы (1. 10)). Разумеется, при этом теория относительности рухнет, как карточный домик. Но с этим, господа, уже ничего не поделаешь. «Чему быть, того не миновать».
Отметим, наконец; то, что физики проводят измерения, на деле означает, что они отвергают теорию относительности (в неявной форме). На словах же (в статьях, журналах, книгах) они её принимают и даже готовы её отстаивать. Но подходящее ли дело для физика, отстаивать иллюзии?
Глава 3. Гипотеза расширения Вселенной и реальные периодические процессы
3. 1. Постановка задачи
В этой главе мы будем обсуждать вопросы, связанные с объяснением явления красного смещения, о котором написано очень много. Мы укажем лишь [2, с. 348]. В следующем пункте мы покажем, что гипотеза расширения Вселенной, якобы объясняющая красное смещение, не выдерживает критики. А потому наша цель: найти красному смещению более правдоподобное объяснение, нежели вышеупомянутая гипотеза.
Здесь используются материалы изданной недавно книги [1 с. 35 -55]. Некоторые вопросы изложены более подробно. Буквенные обозначения здесь такие же, как и в предыдущих главах: tχ – показания часов, t – истинное время. Кроме того, во всех дальнейших рассуждениях скорость света (c) считается постоянной, а приборы наблюдения и источники света – неподвижны относительно друг друга.
3. 2. Гипотеза расширения Вселенной
Ключом к пониманию этой гипотезы является отношение физика и астронома к понятиям «относительного и абсолютного». Когда физик или астроном произносят фразу «Вселенная расширяется» они, тем самым, стараются присвоить понятию расширения абсолютный смысл, хотя прекрасно знают, что этого делать не следует. В самом деле: понятия расширения и сжатия – относительны, также как и понятие движения. Что означает это на практике? Это значит: если в какой-то системе координат имеется нечто, что расширяется, то в этой же системе координат всегда найдется достаточно удаленная от начала координат точка, относительно которой это нечто сжимается. Фраза «Вселенная расширяется» не содержит в себе сведений о системе координат, в которой нам надлежит рассматривать расширение или сжатие, а потому понятие расширения становится абсолютным, а значит и не имеющим физического смысла. Земля, как единственная точка во Вселенной, не образует системы координат; для этого нужно иметь не менее четырех, неподвижных относительно друг друга точек, не лежащих в одной плоскости. Высказывание «Вселенная расширяется» приобретает физический смысл только тогда, когда будет указана система координат, относительно которой происходит расширение.
Пусть имеются три наблюдателя в точках A1, A2, A3, удаленные друг от друга на весьма большие расстояния. Для простоты допустим, что они находятся на одной прямой, а наблюдатель A2 находится точно на середине отрезка A1A3. У наблюдателей имеются приборы наблюдения, такие же, как на Земле. Здесь не надо забывать, что наблюдатели не принадлежат Вселенной, за которой ведут наблюдение. В макромире наблюдатель никогда не принадлежит той системе, за которой он наблюдает (подобно тому, как метр не принадлежит отрезку, длину которого он измеряет). Поэтому наблюдатели A1, A2, A3 образуют свою (жесткую) систему координат. В этой системе они неподвижны относительно друг друга. Только после того (но не раньше), как у нас появится эта система координат, наши рассуждения о расширении Вселенной приобретут физический смысл.
Пусть наблюдатель в точке A1 фиксирует факт – «приборы показывают, что относительно точки A1 Вселенная расширяется », а наблюдатель в точке A3 фиксирует факт – «приборы показывают, что относительно точки A3 Вселенная расширяется». Что тогда должен будет зафиксировать наблюдатель в точке A2 в середине отрезка A1A3? Ведь наблюдатель A2 неподвижен относительно A1 и A3. Он обязан зафиксировать факт сжатия Вселенной вдоль прямой A1A3. Этот случай можно обобщить далее. Если три наблюдателя находятся в вершинах (жесткого) треугольника ABC и фиксируют расширение Вселенной, то всегда найдется не менее трех наблюдателей, которые будут фиксировать сжатие Вселенной. Как легко видеть, три из этих наблюдателей будут находиться по серединам сторон треугольника ABC и фиксировать сжатие Вселенной вдоль сторон этого треугольника. Теперь аналогично можно расположить четырех наблюдателей в вершинах тетраэдра ABCD и сделать заключение: если приборы в вершинах тетраэдра фиксируют расширение Вселенной, то на серединах рёбер тетраэдра приборы обязательно зафиксируют её сжатие. И так далее. Таким образом, если мы верны принципам относительности, нам обязательно придется говорить не только о тех частях Вселенной, которые расширяются, но и о тех её частях, которые сжимаются. Но нам не обязательно говорить о тех частях Вселенной, которые сжимаются, если мы не верны принципам относительности. Но тогда придется отрицать и всю физику; вся физика построена на принципах относительности.
А что же показывает эксперимент? Он показывает, что центр расширения Вселенной всегда находится там, где находятся приборы наблюдения. Мы твердо в этом уверены потому, что мы знаем; Земля ничем не отличается от других тел во Вселенной, и в любой другой точке Вселенной приборы будут показывать то же, что и на Земле. Таким образом, чтобы остаться верным и принципам логики и принципам относительности и экспериментальным фактам, нам остается единственный вариант – допустить истинность следующего утверждения: никакого реального центра расширения Вселенной не существует, мнимые центры расширения создаются самими приборами в тех точках, где они находятся.
А это означает, что в наших измерениях что-то не так. Что-то не так означает: мы не учитываем в своих измерениях чего-то такого, что следовало бы учитывать. По ходу размышлений выяснилось, что мы не учитываем различия между идеальными и реальными периодическими процессами. Мы знаем одно из этих различий: в отличие от идеальных, реальные периодические процессы всегда конечны и во времени и в пространстве. Но есть еще одно принципиально важное отличие. О нем мы и будем говорить далее в этой главе.
3. 3. Гипотеза о неравенстве нулю времени регистрации события
Указанное выше отличие реальных периодических процессов от идеальных, мы будем выяснять на примере анализа работы часов, как периодически действующего устройства. А затем, используя аналогию, мы распространим полученные выводы на любые периодические процессы.
Поскольку сначала речь пойдет о часах, то мы ограничимся анализом работы только световых часов. Это оправдывается тем фактом, что любые часы можно в принципе заменить эквивалентными световыми часами и все, что верно для световых часов, верно и для остальных часов.
Мы начнем анализ реальных периодических процессов с самого простого предположения, подтверждаемого обыденным опытом. Введем гипотезу:
Регистрация (отметка) о том, что некоторое простое (элементарное) событие произошло, не может быть сделана за время равное нулю, для этого природа отводит некоторое, минимально возможное время, отличное от нуля. Заметим, что эта гипотеза не противоречит нуль – соглашению (см. Гл. 1). Физик в своих формулах должен учитывать время отводимое природой на регистрацию события. Сам же физик по договоренности с математиком продолжает делать свои отметки за время равное нулю.
В науке часто бывает так, что наличие или отсутствие этой гипотезы пренебрежимо мало влияет на результаты измерений. В этом случае об этой гипотезе не вспоминают. Но когда речь идет об измерении очень больших промежутков времени ее нужно помнить, так как время регистрации событий обладает свойством накапливаться в общем измеренном времени.
Заметим еще, что эта гипотеза гораздо более правдоподобна, нежели гипотеза расширения Вселенной. Она, ни каким образом, не противоречит ни логике, ни принципам относительности, ни экспериментальным фактам, ни другим принципиальным основаниям физики.
3. 4. Идеальные световые часы
Кратко изложим принцип работы световых часов (который можно назвать традиционным). Генератор коротких световых импульсов посылает их в направлении отражающего зеркала, которое расположено от генератора на расстоянии s/2. Первый импульс, отразившись от зеркала, возвращается к генератору и попадает в детектор, расположенный рядом с генератором. Время движения импульса на пути «туда и обратно» равно t = s/c. В свою очередь сигнал из детектора от вернувшегося первого светового импульса, подается на генератор и на счетчик. В результате генератор запускается и посылает на зеркало второй световой импульс, что означает начало второго периода, а на счетчике появляется единица, что означает окончание первого периода. И так далее. Между вернувшимся импульсом и вновь отправляемым импульсом имеется задержка во времени, обусловленная электроникой часов, назовем ее τэл (τ – далее, греч. тау). Эта задержка должна быть включена в длительность периода часов. Итак, период часов (далее Tχ) равен Tχ = s/c + τэл. Время τэл должно быть по возможности минимальным, но не менее важно, чтобы оно было постоянным. На рис. 3. 1 изображен график хода таких часов.
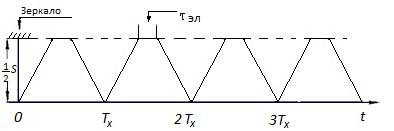
Рис. 3. 1
Здесь по горизонтали отложено время, а по вертикали отложено расстояние s/2 от генератора до зеркала. Чтобы не загромождать рисунок (на оси времени позже мы предполагаем изобразить более важные для нас отрезки времени), время задержки τэл мы расположили на зеркале. Это не меняет сути дела.
3. 5. Реальные световые часы
В предыдущем пункте мы не случайно назвали часы идеальными, так как введенная нами гипотеза (см. пункт 3. 3.) не принималась во внимание. Пусть теперь гипотеза имеет место и для регистрации (отметки) одного элементарного события требуется время τ. Чтобы максимально упростить первоначальные рассуждения, мы конкретизируем эту гипотезу дополнительным условием. Мы допустим, что τ не только отлично от нуля, но также оно постоянно для каждых конкретных часов.
Элементарное событие это такое событие, которое не содержит никаких других подсобытий, кроме самого себя и невозможного. Начнем с 1-го периода. После того как 1-й период закончится, часы должны остановиться на время регистрации события: «первый период закончился». Но разве часы не могут работать дальше, не дожидаясь окончания регистрации? Не могут! Для уяснения этого рассмотрим аналогичные измерения длины. Мы откладываем на прямой один за другим отрезки при помощи циркуля, который в нашем случае является измерительным инструментом и эталоном длины. Циркуль не может быть переставлен для откладывания следующего отрезка прежде, чем он не сделает отметку (засечку) на прямой. Но события: «засечка сделана», «данный отрезок отложен», «регистрация закончена» это – эквивалентные события. Точно также все происходит и в часах. Второй период не может начаться потому, что неизвестно откуда он должен начинаться, пока отметки об окончании первого периода еще нет.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.



