Со спичками не шутят

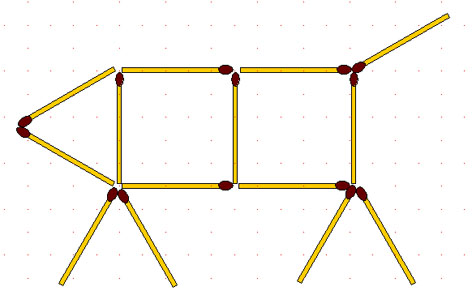
2-96. Поросёнок. Передвинув как можно меньше спичек, заставьте поросёнка повернуться в противоположную сторону.

2-97. Стрела. Из 16 спичек выложена стрела:

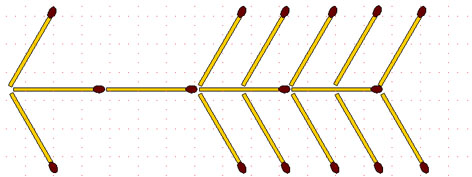
а) переложите 8 спичек так, чтобы получилось 8 равных треугольников;

б) переложите 7 спичек так, чтобы получилось 5 равных четырёхугольников.

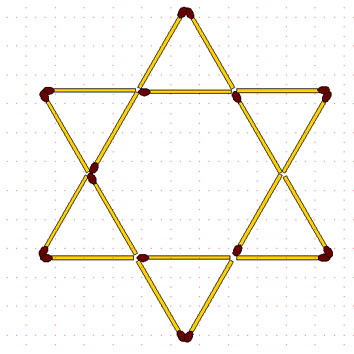
2-98. Звезда-2. Переложите 6 спичек так, чтобы получилось 6 равных симметрично расположенных четырёхугольников.

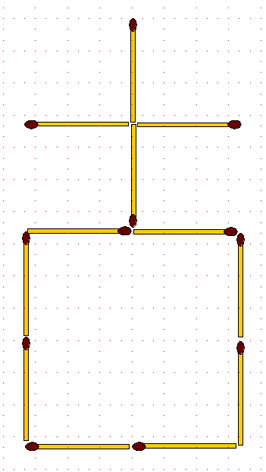
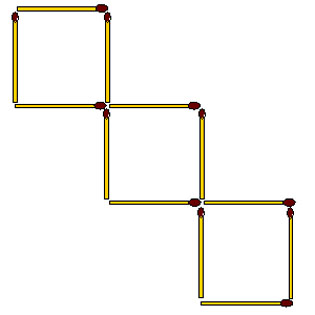
2-99. Зигзаг. Переложите 8 спичек так, чтобы получилось 2 неравных квадрата.

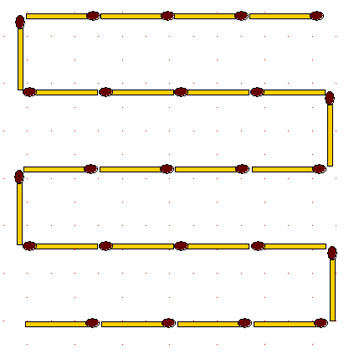
2-100. Изгородь. Переложите 14 спичек так, чтобы получилось 3 квадрата.

2-101. Спираль. Спираль из 35 спичек закручена против часовой стрелки. Переложите 4 спички так, чтобы получилась такая же спираль, но закрученная по часовой стрелке.

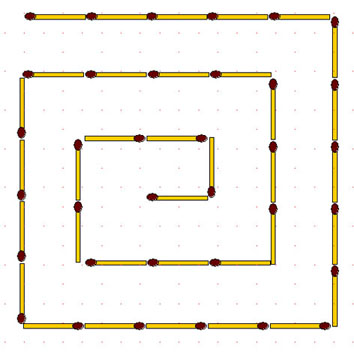
2-102. Спираль-2. В такой же спирали из 35 спичек переложите 4 спички так, чтобы получилось 3 неравных квадрата.

Раздел В. Площади фигур.

Примем за единицу длины – длину одной спички. Тогда площадь квадрата, сложенного из 4 спичек, будет составлять одну условную квадратную единицу (у. кв. ед.). Надеемся, что читатель обладает знаниями о площадях плоских фигур в объёме средней школы и ему не составит труда применить простейшие формулы для вычисления площади прямоугольника, параллелограмма, ромба, трапеции, правильных многоугольников или фигур составленных из этих простейших.

2-103. На рисунке изображен четырёхугольник из 6 спичек, площадь которого вдвое больше площади квадрата со стороной, равной одной спичке. Задача состоит в том, чтобы изменить форму четырёхугольника, не изменяя его периметра, так, чтобы площадь уменьшилась:

а) вдвое; б) вчетверо.

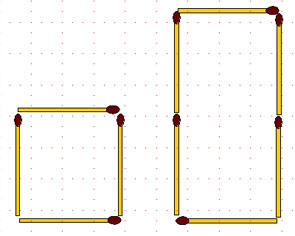
2-104. Из 6 спичек сложены прямоугольник и равносторонний треугольник. Периметры этих фигур одинаковы, а у какой больше площадь?

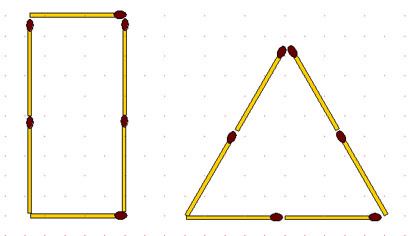
2-105. Из 6 спичек можно составить различные фигуры. Некоторые из них изображены на предыдущем рисунке. Спрашивается, у какой фигуры, составленной из 6 спичек, самая большая площадь?

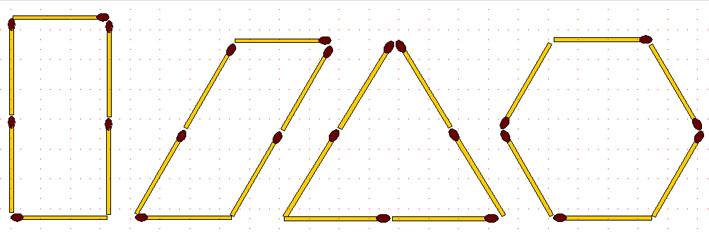
2-106. Из 8 спичек можно составить ещё больше различных замкнутых фигур. Некоторые из них представлены на рисунке. Площади фигур различны. Сложите из 8 спичек фигуру с наибольшей площадью.

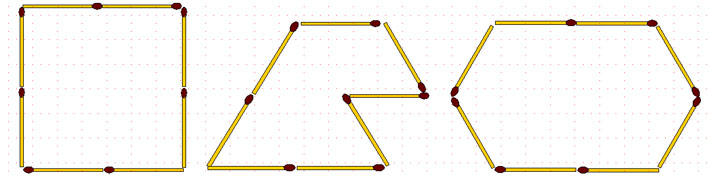
2-107. С помощью 4 спичек можно построить квадрат площадью 1 у. кв. ед. Сколько спичек потребуется, чтобы построить фигуру, имеющую площадь не менее 10 у. кв. ед.?

2-108. Дано 12 спичек. Требуется сложить фигуру, имеющую площадь 3 у. кв. ед. (Исключим простейший случай, показанный на рисунке к задаче 2-37).

2-109. Из 12 спичек можно сложить фигуру площадью 9 у. кв. ед. Переложив 8 спичек, уменьшите площадь на 4 у. кв. ед.

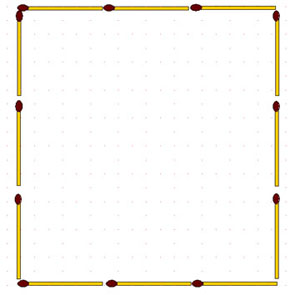
2-110. Постройте из 12 спичек фигуру площадью ровно 4 у. кв. ед.

2-111. Из 20 спичек составлены два прямоугольника: один из 14 спичек, а другой – из 6. Ясно, что площадь второго прямоугольника в 3 раза меньше площади первого. Сломайте данные фигуры и составьте новые, снова из 14 и из 6 спичек, причём с тем же отношением площадей.

2-112. Площадь прямоугольника из 14 спичек в 3 раза больше площади прямоугольника, составленного из 6 спичек. Теперь возьмите 1 спичку в большей группе, переложите её в меньшую и с помощью 7 и 13 спичек ограничьте снова две фигуры, из которых площадь одной была бы ровно в 3 раза больше площади другой.

2-113.

Соотношение площадей фигур 1:3. Теперь возьмите 1 спичку в большей группе, переложите её в меньшую, и постройте новые фигуры с тем же соотношением площадей. Только сделайте это так, чтобы 12 спичек из первоначального расположения остались на своих местах.

2-114. Примем за среднюю длину спички 5 сантиметров. Сколько потребуется спичек, чтобы выложить равными квадратами со стороной в одну спичку один квадратный метр?

Раздел Г. Деление фигуры на заданные части и разное.

2-115. Данную фигуру разделите на 4 одинаковые части с помощью 5 спичек.

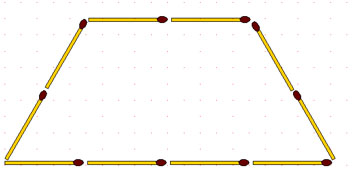
2-116. Фигуру, составленную из 16 спичек, разделите спичками на две одинаковые части.

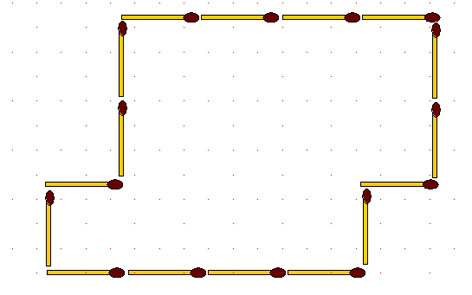
2-117. С помощью 7 спичек, разделите фигуру на 3 одинаковые части.

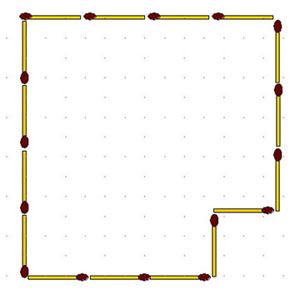
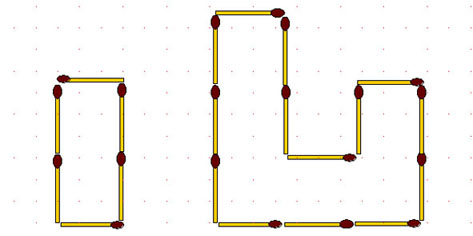
2-118. Данную фигуру (рис. ниже слева) разделите на 4 одинаковые части с помощью 8 спичек.

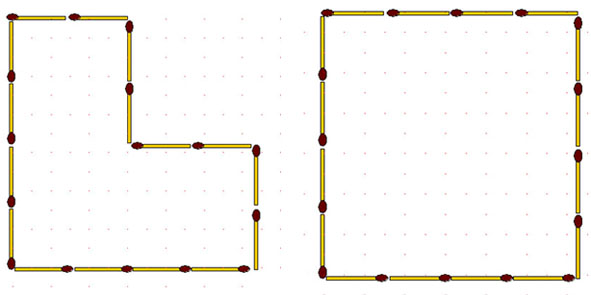
2-119. Квадрат ограничивают 16 спичек (рис. выше справа). Требуется разделить его на 4 фигуры площадью по 4 у. кв. ед. каждая с помощью 8, 10, 12 спичек (три задания). Разумеется, нельзя класть две спички на одну и ту же сторону. Труднее выполнить условие, используя 11 спичек (четвертое задание).

2-120. Выложенные в форме квадрата 16 спичек представляют изгородь двора. Часть площади двора занята домом, изображенным в виде квадрата из 4 спичек. Остальную часть двора требуется разделить при помощи 10 спичек на 5 участков, одинаковых по форме и по площади.

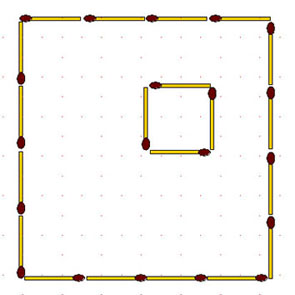
2-121. Данную фигуру разделите на 4 одинаковые части с помощью 8 спичек.

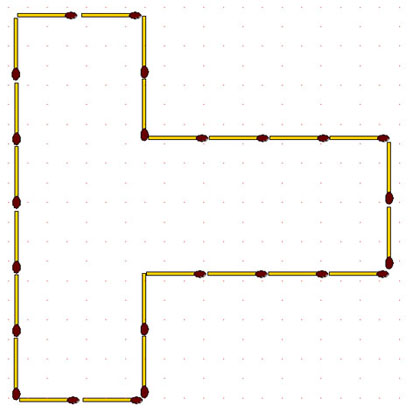
2-122. Сад, очертание которого изображено 20 спичками, и в середине которого находится дом квадратной формы, требуется:

а) разделить 18-ю спичками на 6 равновеликих и одинаковых по форме частей;

б) разделить 20-ю спичками на 8 одинаковых частей.

Раздел Д. Различные дополнения к геометрии, не вошедшие в предыдущие разделы по разным причинам.

Две задачи отличаются тем, что для их формулировки и решения, кроме спичек, нужен соответствующий рисунок на бумаге.

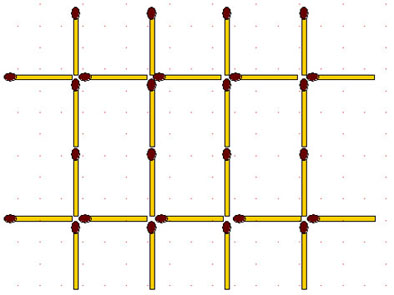
2-123. Сторона каждого маленького квадрата на рисунке, имеет длину в одну спичку. Требуется разместить ровно 26 спичек вдоль линий таким образом, чтобы они разделили весь чертёж на две части одинаковых размеров и формы, причем в одной из них должны находиться два нарисованных треугольника, а в другой – два круга.

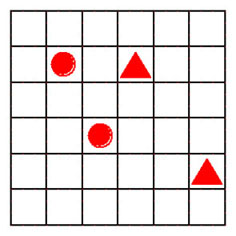
2-124. На бумаге начерчен квадрат со стороной равной длине 4 спичек и прямыми линиями разделён на 16 меньших квадратов.

Задача состоит в том, чтобы расположить спички на листе выполняя три условия:

1) каждая спичка должна закрывать сторону одного из маленьких квадратов;

2) у каждого из маленьких квадратов ровно 2 стороны должны быть закрыты спичками;

3) спички нельзя размещать, на краю большого квадрата, то есть по внешним сторонам.

Решите ту же задачу для исходного квадрата с длиной стороны в 5 спичек.

Отдохнем от решения заданий. На уроках школьной геометрии, прежде чем решать задачи, учитель объясняет соответствующие теоремы и доказывает их. Оказывается и теоремы можно доказывать «на спичках». Очень важной для всего курса геометрии является теорема о сумме внутренних углов треугольника. Вот как можно доказать ее с помощью простой спички. Начертив на доске треугольник, положим на одну из его сторон (например, в вершине А) спичку, направленную головкой от точки А в сторону точки В.

Далее, следуя рисунку, будем двигать спичку вдоль стороны, до тех пор, пока ее головка не совпадет с вершиной В. Теперь, поворачиваем спичку так, чтобы она описала угол В и расположилась вдоль другой стороны треугольника. Сдвинем теперь спичку вдоль второй стороны до следующей вершины С и поворачиваем спичку так, чтобы она описала угол С. Далее сдвинем спичку вдоль третьей стороны до исходной вершины А, поворачиваем спичку так, чтобы она описала угол А и вернулась в исходное положение, повернувшись при этом на все три угла треугольника, причем строго по часовой стрелке. В итоге она окажется совмещенной с первоначальной стороной треугольника, но ее головка «смотрит» в противоположное направление. Угол, описанный спичкой, равен сумме внутренних углов треугольника, а с другой стороны её суммарный поворот равен развернутому углу, то есть 1800. Этот метод доказательства называется «метод скользящей спички». Им можно воспользоваться для определения суммы внутренних углов четырехугольника, он служит удобным способом измерения углов любых многоугольников с любыми сложными самопересечениями.

Серьезные рассуждения подготовили нас к серьезным задачам. Спичечный коробок по форме представляет собой прямоугольный параллелепипед.

2-125. Как измерить диагональ спичечной коробки с помощью простой линейки? Нужно обойтись без вычислений, без формулы для квадрата диагонали, который равен сумме квадратов трех измерений параллелепипеда. Стороны параллелепипеда измеряются элементарно, а вот диагональ?

2-126. Воткните в яблоко с двух диаметрально противоположных сторон две спички.

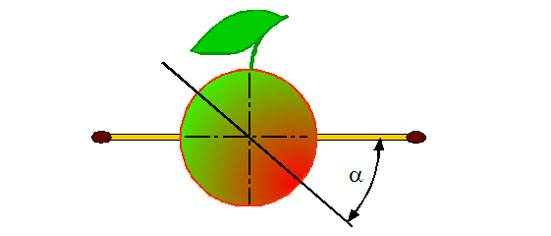
Если такое яблоко разрезать под некоторым углом α и поворачивать одну половинку относительно другой, то угол между спичками будет изменяться и за пол-оборота достигнет наименьшего значения (какого?).

Разрежьте это яблоко с таким расчетом, чтобы значение наименьшего угла не могло превысить 900. Совместите обе половинки так, чтобы между спичками образовался угол 1200. Считайте, что яблоко имеет точную форму шара.

2-127. Сколько всего спичек может быть получено из деревянного куба, ребро которого 1 метр? Каждая спичка должна иметь длину 5 см и поперечное сечение 2×2 мм. Вопрос нужно решить чисто теоретически, считая распил идеальным, то есть на него объем не расходуется.

Теперь еще раз пройдемся по фигурам, увеличивая постепенно количество используемых спичек.

2-128. Из 4 спичек сложен крест, но не так как в задаче 2-6. Получить маленький квадратик в центре не получится. Хотя требование аналогичное: переместить одну спичку так, чтобы получился квадрат.

2-129. Из 5 спичек сложена маленькая стрела. Переложите 3 спички так, чтобы стрела поменяла направление на противоположное.

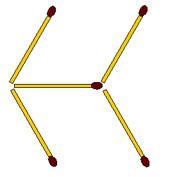
2-130. Из 6 спичек сложен правильный шестиугольник, у которого все углы тупые по 1200. Требуется переложить 4 спички так, чтобы получились треугольники с острыми углами.

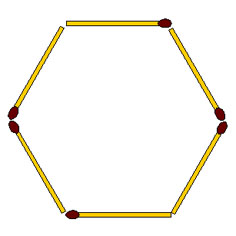
2-131. Как переложить 2 спички так, чтобы из трех треугольников получилось два треугольника.

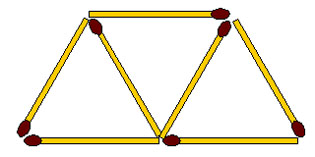
2-132. Из 8 спичек сложите 3 квадрата.

2-133. Переложите 2 спички так, чтобы получилось три квадрата одного размера.

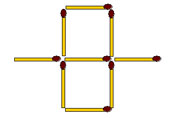
2-134. Переложите 3 спички, чтобы вместо трех треугольников получить три четырехугольника одного размера.

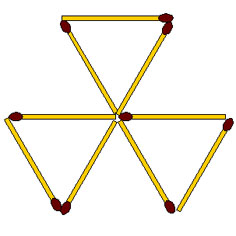
2-135. Из 9 спичек составьте 7 треугольников, лежащих в одной плоскости. Ломать, разрезать и накладывать спички друг на друга не допускается. Есть два решения.

2-136. Из заданной фигуры получите два равносторонних треугольника, убрав 4, или 3, или 2 спички.

2-137. Из 10 спичек сложены три квадрата. Такая фигура уже была в задачах 2-27 и 2-28, но для нее есть еще задачи.

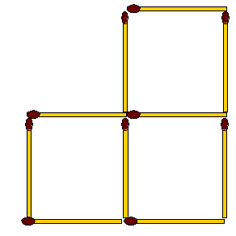
а) переложите 2 спички так, чтобы получился один большой и один маленький квадрат;

б) добавьте 2 спички так, чтобы получилось четыре одинаковых маленьких квадрата и еще один большой квадрат.

2-138. Переложите 3 спички так, чтобы получилось четыре равных четырехугольника.

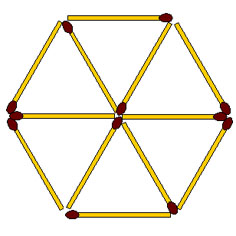
2-139. Переложите 4 спички так, чтобы получилось четыре равных квадрата и один большой.

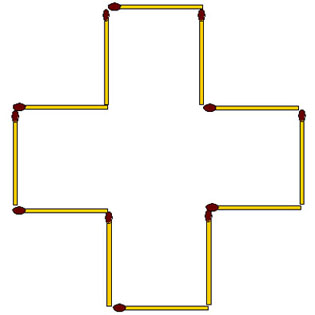
2-140. Из 12 спичек сложен крест, площадь которого равна 5 условным квадратам. Измените расположение спичек так, чтобы контур фигуры охватывал площадь равную только 4 условным квадратам.

2-141. Из 22 спичек требуется сложить прямоугольник наибольшей площади.

2-142. Можно ли из 36 спичек, не ломая их, сложить прямоугольный треугольник?

Урок 3. Алгебра

Суперакция от спичечной фабрики Дремлесдрев:

Каждая пятая спичка в коробке … зажигается!

Основные разделы математики, изучаемые в средней школе – это арифметика, геометрия и алгебра. Считается, что математика, помимо своего прикладного практического значения, развивает логическое мышление. Поэтому первыми в раздел алгебры мы включили несколько задач, в которых не нужно производить какие-либо математические действия, а требуются только логические рассуждения, просчет и перебор комбинаций на несколько шагов вперед.

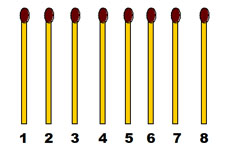
3-1. Разложите в ряд 8 спичек и, перекладывая одну спичку через две, составьте в четыре хода 4 группы по 2 спички в каждой.

Чтобы стало понятнее, как это нужно сделать, дадим маленькую подсказку, покажем конечный результат. Должно получиться так:

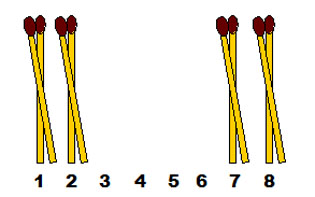
3-2. Десять спичек положите в один ряд. Требуется собрать их попарно, всего в пять пар, перекладывая по одной спичке через две, за наименьшее число ходов.

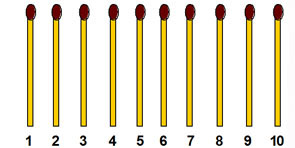
3-3. Пятнадцать спичек сложены в ряд. Требуется собрать их в пять групп по 3 спички в каждой. Перекладывать спички можно только по одной, каждый раз через 3 спички, Решите задачу за 10 ходов.

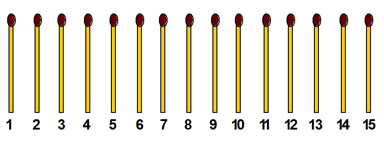
3-4. Сосчитайте 22 спички, разложенные так, как показано на рисунке, подряд по часовой стрелке, выбрасывая каждую седьмую спичку. Начать счет нужно с такой спички, чтобы выброшенными оказались все спички кроме той, которая лежит отдельно. Вопрос в том, с какой спички начать счет?

3-5. Семь спичек разложите на столе звездочкой, а ещё 6 спичек возьмите в руку. Начиная от любой спички, отсчитайте по часовой стрелке третью и рядом положите ещё одну спичку. Затем опять, начиная от любой спички, в том же направлении, отсчитайте третью спичку, против которой ещё не лежит дополнительная спичка, и также положите около неё ещё одну спичку. Действуя таким образом, постарайтесь разложить все 6 спичек, которые были у вас в руке. При отсчете спичек не следует пропускать и те, около которых уже положена спичка. Как решить задачу?

3-6. Тринадцать спичек расположены расходящимися лучами, как показано на рисунке, причем 12 из них направлены от центра и только одна – к центру. Требуется снять все спички, кроме той, которая обращена к центру, соблюдая следующее правило: сначала снять одну спичку, а затем, двигаясь по часовой стрелке, снимать каждую тринадцатую спичку. Сообразите, с какой спички нужно начать?

Получается как в детской считалочке из 13 слов, считаем по кругу и спичку, на которую выпадет счет, выводим из игры. Главное – какую убрать первой, дальше элементарно.

В нашем представлении спичка символизирует нечто маленькое. Есть даже выражение «измерять на спичках», означающее какие-то мелкие придирки. Действительно, длина спички чуть больше 4 сантиметров, а вес её, наверное, меньше 1 грамма. Вот если бы Гулливер прихватил с собой спички в страну лилипутов, то для них она выглядела бы в 12 раз больше и представляла бы собой деревянную палку длиной 50 сантиметров. Но оказывается, математика может доказать, что спичка и без страны лилипутов имеет внушительные размеры. Это делается с помощью софизмов – ложных по существу умозаключений, формально кажущихся правильными. Любой софизм основывается на преднамеренном, сознательном нарушении правил логики или математики. Сейчас мы рассмотрим два подобных утверждения.

3-7. Софизм: спичка вдвое длиннее телеграфного столба.

Пусть a – длина спички (в сантиметрах), b – длина столба (тоже в сантиметрах). Обозначим b-a=c, тогда b=a+c. Перемножим эти равенства почленно. Получим b2-ab=ca+c2. Вычтем из обеих частей bc. Получим: b2-ab-bc=ca+c2-bc. Вынесем общие множители за скобки: b(b-a-c)=c(-b+a+c), или b(b-a-c)=-c(b-a-c).

Разделим обе части равенства на одно и тоже выражение (b-a-c). Получим b=-c. Но по первоначальному обозначению c=b-a, так что -c=a-b. Таким образом, окончательно получаем b=a-b, a=2b и спичка оказалась вдвое длиннее телеграфного столба! Найдите ошибку в рассуждениях, или может быть всё правильно?

3-8. Софизм: вес спички равен весу слона.

Оказывается спичка не только очень длинная, но и очень тяжелая! Пусть – x вес слона, а – y вес спички. Обозначим сумму весов через 2v, то есть, x+y=2v. Из этого равенства переносом слагаемых в другую часть можно получить ещё два равенства: x-2v=-y, и x=-y+2v.

Перемножим почленно последние два равенства:

x2-2vx=y2-2vy.

Прибавив к обеим частям полученного равенства по v2.

Получим x2-2vx+v2=y2-2vy+v2 или (x-v)2=(y-v)2.

Извлекая квадратный корень из обеих частей последнего равенства, получим: x-v=y-v или x=y, то есть вес слона равен весу спички. Найдите ошибку в рассуждениях.

Следующая группа состоит из задач, которые можно решать логически, а можно составлять уравнения. Это как раз то, чем занимается школьная алгебра: обозначить неизвестные величины, составить и решить уравнения, найти и проверить ответ.

3-9. В коробке лежали спички. Их количество удвоили, а затем убрали 8 спичек. Остаток спичек снова удвоили, а затем снова отняли 8 спичек. Когда эту операцию проделали в третий раз, в коробке не осталось ни одной спички. Сколько их было сначала?

3-10. Спички лежат в двух кучках. Если из первой кучки переложить 2 спички во вторую, то во второй спичек будет в 5 раз больше, чем в первой. Если же из второй кучки переложить в первую 5 спичек, то в первой будет в 3 раза больше, чем во второй. Сколько спичек в каждой кучке?

3-11. Положите на стол три кучки спичек. В одну кучку положите 11 спичек, в другую – 7, в третью – 6. Перекладывая спички из любой кучки в любую другую, нужно сравнять все три кучки, чтобы в каждой было по 8 спичек. Только при перекладывании требуется соблюдать правило: к любой кучке разрешается добавлять ровно столько спичек, сколько в ней есть. Например, если в кучке 6 спичек, то и добавить к ней можно только 6 спичек. Задача решается за три хода!

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.